BIHAR BOARD CLASS 8TH MATH | क्षेत्रमिति
BIHAR BOARD CLASS 8TH MATH | क्षेत्रमिति
बन्द समतल आकृति की सीमाओं की कुल दूरी उसका परिमाप कहलाती है तथा घिरा हुआ
क्षेत्र क्षेत्रफल कहलाता है।
इस क्षेत्रफल का अध्ययन क्षेत्रमिति कहलाता है।
जैसे― वृत्त का क्षे० = πr²
आयत का क्षे = ल.×चौ.
वर्ग का क्षे० =(भु०)²
प्रश्नावली-13.1
1. बगल की आकृतियों में एक आयताकार और एक वर्गाकार खेल के मैदान के माप दिए
हुए हैं। यदि इनके परिमाप समान हैं तो किस मैदान का क्षेत्रफल अधिक होगा।
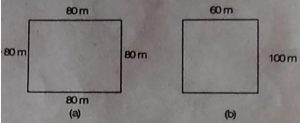
वर्ग का परिमाप =4×80=320 m²
आयत का परिमाप = 2(60+ 100)= 2 ×160 = 320 m²
वर्ग का क्षे. = (80)² = 6400 m²
आयत का क्षे. = 60 ×100 = 6000 m²
वर्ग का क्षेत्रफल अधिक है।
2. विमला के पास एक आयताकार प्लॉट है (जैसा कि चित्र में दिखाया गया है) वह
प्लॉट के बीच में एक वर्गाकार घर बनाना चाहती है। घर के चारों ओर फुलवारी
लगवानी है। उसे फुलवारी लगाने में 40 रु. प्रति वर्गमीटर की दर से कितने रुपये
खर्च करने होंगे?
उत्तर― प्लॉट का कुल क्षे. = 80×60 = 4800 m²
घर का क्षे. = (40)² = 1600 m²
बची हुई जगह = 4800—1600 = 3200 m²
फुलवारी की जगह = 3200 m²
कीमत 3200×40 = 128000 m²
3. अमरेश अपने घर के आंगन में ईंट बिछवाना चाहता है। यदि आँगन की लम्बाई 20
मीटर और चौड़ाई 15 मीटर हो तो एक ईंट की लम्बाई 25 सेमी. और 80 सेमी. हो
तो उस आँगन में कितने ईंटें लगेंगी? (कच्चा चित्र बिना हल करें)।
उत्तर—

आँगन का कुल क्षे. = 20 × 15 = 300 m²
ईंट का क्षे० = 25×80 = 2000 cm
= 2 m
ईंटों की सं. = 300m²/2m = 150 ईटें
4. एक त्रिभुजाकार खेत का क्षेत्रफल 600 वर्गमीटर तथा ऊंँचाई 60 मीटर है तो उस खेत
का आधार ज्ञात करें।
उत्तर― क्षे. = 600 m²
ऊँ = 60 m
∆ का क्षे• = 1/2×आ•×ऊँ•
600 = 1/2×x×60
600×2/60 = x
x = 20m
5. एक धावक को कम से कम दूरी तय करने के लिए निम्न में से किस आकृति पर
चक्कर लगाना चाहिए? आप जानते हैं कि सम्पूर्ण वृत्त की परिधि का सूत्र c=2πr
जहाँ r वृत्त की त्रिज्या है।
उत्तर―(a) अर्धवृत्त की परिधि =πr
= 22/7×42×2 = 44m
(b) ∆ की परिधि =3× भु.
= 14×3= 42 m
(c) वृत्त की परिधि =2πr
= 2× 22/7 ×14 = 88m
सबसे कम क्षे० =b
विभिन्न आकृतियों का क्षे.
समलम्ब चतुर्भुज का क्षे. = 1/2×h(b1+b2)
= 1/2× ऊँचाई (समान्तर भुजाओं का योग)
समचतुर्भुज का क्षे.= 1/2× d1×d2
= 1/2× विकर्ण1 × विकर्ण2
प्रश्नावली-13.2
1. एक समलम्ब चतुर्भुज PQRS के P और S समकोण है। इसकी भुजाओं की माप
चित्र में दर्शाई गई है, समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
उत्तर― समलम्ब □ का क्षे० = 1/2×h×(b1+b2)
= 1/2×13 cm × (20+25)
= 1/2×12×45 = 270 m²
2. एक समलम्ब चतुर्भुज ABCD में AB, CD का समान्तर है AB = 30 सेमी., BC=
15 सेमी., DC = 44 सेमी. और AD = 13 सेमी.। समलम्ब चतुर्भुज का क्षेत्रफल
ज्ञात कीजिए।
उत्तर—
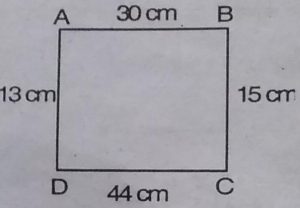
समलम्ब चतुर्भुज का क्षे. = 1/2×h× (b1 + b2)
= 1/2×13× (30+44)
= 1/2×13×37=841 m²
3. किसी समलम्ब चतुर्भुज की समानान्तर भुजाएँ 52 सेमी. और 27 सेमी. है तथा अन्य
दो भुजाएँ 25 सेमी. और 30 सेमी. की हैं। समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
उत्तर—
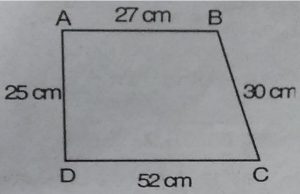
ABCD□ का क्षे. = 1/2×25×(27+52)
= 1/2×25×79
= 1975/2 =987.5 = 988
4. किसी समलम्ब चतुर्भुज का क्षेत्रफल 200 मी.² है और इसकी ऊंँचाई 8 मी. है। यदि
समान्तर भुजाओं में एक भुजा दूसरी भुजा से 6 मी. अधिक है तो समान्तर भुजाओं की
लम्बाई ज्ञात कीजिए।
उत्तर― माना एक भुजा = x
दूसरी भुजा = 6 +x
x=8m
समलंब का क्षे. = 1/2×h×(b1+b2)
200 = 1/2×8×(x+x+6)
200×2/8 = 2x+6
50 = 2x+6
50―6 = 2x
= 2x = 44
x = 44/2
x = 22
एक भुजा = 22 m
दूसरी भुजा =x+6= 22+6=28 m
5. किसी समलम्ब चतुर्भुज की समान्तर भुजाएँ क्रमशः 24 सेमी. और 20 सेमी. हैं तथा
दोनों भुजाओं के बीच की दूरी 15 सेमी. है, इसका क्षेत्रफल ज्ञात कीजिए।
उत्तर― h=15m
b1 =24cm
b2 =20m
□ का क्षे• = 1/2×h×(b1+b2)
= 1/2×15× (24+20)
= 1/2×15×44 = 330 cm²
6. किसी समलम्ब चतुर्भुज का क्षेत्रफल 384 सेमी.² है। यदि समान्तर भुजाओं का
अनुपात 3:5 हो और दोनों की लम्बात्मक दूरी 12 सेमी. हो तो प्रत्येक समान्तर भुजाओं
की माप ज्ञात कीजिए।
उत्तर— h = 12 cm
b1 = 3x
b2 = 5x
□ का क्षे•= 1/2×h× (b1 + b2)
384 = 1/2×12× (3x+5x)
384×2/12=8x
64 = 8x
64/8 = x
x = 8
पहली भुजा =3x= 8×3 = 24 m
दूसरी भुजा =5x=5×8= 40 m
7. एक समचतुर्भुज की प्रत्येक भुजा 8 सेमी. है और इसका क्षेत्रफल 11.2 सेमी² है तो
इस चतुर्भुज का शीर्ष लम्ब ज्ञात करें।
उत्तर— □ का क्षे० = 1/2×d1×d2 or, b ×h
h = 6 cm
b=10cm
=6cm × 10 cm = 60 m²
8. एक समचतुर्भुज की प्रत्येक भुजा 8 सेमी. है और इसका क्षेत्रफल 11.2 सेमी² है तो
इस चतुर्भुज का शीर्ष लम्ब ज्ञात करें।
उत्तर— समचतुर्भुज का क्षे = b×h
11.2 = 8×h
11.2/8 = h
h = 1.4 cm
9. किसी समचतुर्भुज का क्षेत्रफल 64 सेमी.² है और इसकी परिमाप 64 सेमी. है।
समचतुर्भुज का शीर्ष लम्ब ज्ञात कीजिए।
उत्तर— □ की परिमाप =4×भुजा
=4×x
4/64 =16 = x
x = 16 cm
□ की क्षे० = b×h
64 =16×h
64/16 = h
h = 4 cm
10. एक समचतुर्भुजाकार पार्क की प्रत्येक भुजा की लम्बाई 72 मीटर तथा शीर्ष लम्ब 18
मीटर है। उस वर्गाकार खेल के मैदान का भुजा क्या होगी जिसका क्षेत्रफल इस
समचतुर्भुज के क्षेत्रफल के बराबर है ?
उत्तर― □ का क्षे० = b×h
=72×18 = 1296 m²
समचतुर्भुज का क्षे• = वर्ग का क्षे• = 1296 m²
भुजा² = 1296 m²
√1296 = 36 m
11. किसी चतुर्भुज का एक विकर्ण 30 मीटर और सम्मुख शीर्षों से डाले गए लम्ब 10
मी. और 8 मी. हैं तो चतुर्भुज का क्षेत्रफल निकालिए।
उत्तर— □ का क्षे० = ∆ACB+∆+CDB
= 1/2×30×10+1/2×30×8
= 150 + 120 = 270 cm²
12. निम्न आकृति का क्षेत्रफल तथा शीर्ष लम्ब ज्ञात कीजिए।
उत्तर— ∆ PCB का क्षे. = 1/2×आ•×ऊँ•
= 1/2×12×10 = 60 cm²
□ DCPA का क्षे० = भुजा²
= (10)² = 100 cm²
.: आकृति का क्षे = 100 + 60 = 160 cm²
∆ PCB में,
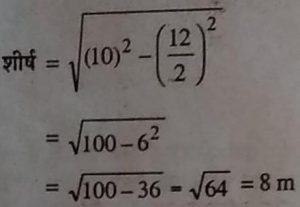
(पाइथागोरस प्रमेय)
ठोस आकार
घन—घन छह पृष्ठों से घिरी हुई आकृति होती है।
घन का क्षेत्रफल =6× भुजा²
= 6h²
घनाभ— घनाभ की आकृति साबुन के डब्बे या ईंट की तरह होती है।
घनाभ का क्षे० = 2(hb + lh + bh)
=2 (लम्बाई × चौ• + चौ• × ऊँ• + ऊँ•× ल•)
बेलन–बेलन की आकृति में एक वक्रपृष्ठ और दो वृत्ताकार सतह होते हैं। यह एक टिन
के बेलनाकार डब्बे की तरह दिखती है।
बेलन का वक्रपृष्ठीय क्षे• =2πrh
बेलन का सम्पूर्ण क्षे• =2πr(r+h)
प्रश्नावली-13.3
1. दिए गए दोनों घनों को जोड़कर एक घनाभ बनाया गया, तो घनाभ के सम्पूर्ण पृष्ठ
का क्षेत्रफल ज्ञात कीजिए।
उत्तर― पहले घन का क्षे =6× भुजा²
=6×8²
=6×64cm² = 384 cm²
दूसरे घन का क्षे• =6×8²cm
=6×64 cm²=384 cm²
.: घनाभ का क्षे• = (384+ 38.4) cm²
= 768 cm²
2. एक धन की एक भुजा 12 सेन्टीमीटर है तो घन का सम्पूर्ण पृष्ठ क्षेत्रफल ज्ञात कीजिए।
उत्तर— घन की भुजा = 12 cm
घन का सम्पूर्ण पृष्ठ क्षे• = 6× भुजा²
=6× (12)²
=6×144=864 cm²
3. एक घनाभाकार पिंड की लम्बाई 15 सेमी., चौड़ाई 14 सेमी. एवं ऊँचाई 13 सेमी. है,
पिंड का पृष्ठ क्षेत्रफल ज्ञात कीजिए।
उत्तर— ल• (l) = 15cm
चौ. (b) = 14cm
ऊँ•(h) = 13 cm
क्षे• = 2(lb + bh + lh)
= 2(15×14+14×13 + 13×15)
= 2 (210+ 182 + 195)
= 2(587)=1174 m²
4. ऐसे घनाभाकार पिंड की भुजा ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 2400 वर्ग मीटर है।
उत्तर— कुल पृष्ठीय क्षे• =6× भुजा²
2400 =6×x²
2400/6 = x²
400 = x²
x = √400 = 20m
5. एक घनाभाकार साबुन की लम्बाई 6 सेमी., चौड़ाई 5 सेमी. एवं सम्पूर्ण पृष्ठ का
क्षेत्रफल 148 वर्ग सेमी. है तो उसकी ऊंँचाई ज्ञात कीजिए।
उत्तर―घनाभाकार साबुन की लं० = 2 (lb + bh+lh)
l= 6cm
b = 5 cm
h = x cm
or, 148 m² = 2(6×5+5×x+6×x)
148 = 2(30+ 5x + 6x)
148 = 2(30+ 11x)
148 = 60+ 22x
148—60 = 22x
88 = 22x
88/22 = x
x =4 cm (ऊंँचाई)
6. एक घनाकार लकड़ी के टुकड़े की एक किनारे की लम्बाई 10 सेमी. है । उसमें से 3
सेमी,×2 सेमी.×1 सेमी. आकार का घनाभ एक कोने से काटकर निकाल दिया गया
तो शेष क्षेत्रफल कितना होगा?
उत्तर―घनाभाकार लकड़ी के टुकड़े का क्षे• =6 × l²
=6×10²
=6×100
=6×100 cm²
घनाभ का क्षे• = 2(1b+ bh + lh)
= 2(3×2+2×1+1×3)
= 2(6+2+3)
=2×11= 22 cm²
शेष क्षे•= (600–22) cm²
= 578 cm²
7. एक बेलन की ऊंँचाई 25 सेमी. है और आधार का क्षेत्रफल 154 वर्ग सेमी. है तो बेलन
के वक्रपृष्ठ का क्षेत्रफल ज्ञात करें।
उत्तर― h=25cm
बेलन का आधार वृत्त का क्षे•= 154 m²
πr² = 154
r² = 154× 7/22
r²=√7×√7
r=7cm
बेलन का सम्पूर्ण पृष्ठीय क्षे•=2πr(r+h)
= 2×22/7×7(7+25)
=2×22/7×7×32 = 1408 m²
8. एक बेलनाकार लकड़ी की लम्बाई 50 सेमी. है तथा आधार की त्रिज्या 14 सेमी. है।
इसके सम्पूर्ण पृष्ठ का क्षेत्रफल ज्ञात करें।
उत्तर— h = 50 cm
r =14cm
सम्पूर्ण पृष्ठ का क्षे• =2πr(r+h)
=2×22/7 × 14 (14+ 50)
=2×22/7×14×64 = 5632 cm²
9. यदि आपको इन आकृतियों को कागज से पूरा-पूरा ढंकना हो तो कम से कम कितने
कागज की आवश्यकता होगी?
उत्तर—(i)
बेलन का क्षे•=2πr(r+h)
h=15cm
r = 7 cm
क्षे• = 2× 22/7×7(15+7)
=2×22/7×7×22 = 968 m²
(ii) घनाभ का क्षे = 2(1b + bh + lh)
= 2(4×6+6×3+3×4)
= 2(24+ 18+ 12)
= 2×54 = 108 m²
10. एक भवन में 20 बेलनाकार खंभे लगे हैं जिसकी ऊँचाई 4 मीटर है तथा त्रिज्या 14
सेमी. है।4 रुपये प्रति वर्गमीटर की दर से वक्रपृष्ठीय क्षेत्रफल में रँगाई करने का खर्च
ज्ञात कीजिए।
उत्तर— h = 4 m
r=14cm
एक बेलन का क्षे• =2πr(r+h)
= 2×22/7 ×14 (14+4)
= 2×22/7×14×18=1584
20 बेलनों का क्षे• = 20 × 1584 = 31680
4 वर्गमीटर की दर से रंगाई का खर्च = 31680/100×4
= 1267.20
घन, घनाभ और बेलन का आयतन
घन का आयतन =l×l×l=l³
घनाभ का आयतन =l×b×h
बेलन का आयतन = आधार का क्षे•×ऊँ•
=πr²×h=πr²h
प्रश्नावली-13.4
1. अ. एक घन में कितनी सतहें होती हैं ?
ब. किसी घनाभ में किनारों की कुल संख्या कितनी है ?
स. घन और घनाभ के सतहों में क्या अंतर है?
द. घन में कितने शीर्ष होते हैं?
उत्तर—(अ) 6 (ब) 12
(स)घन की सतहे सर्वांगसम होती हैं जबकि घनाभ की नहीं होती। (द) 8
2. नीचे घनाभ के किनारों की लम्बाइयाँ दी हुई हैं, उनके—
अ, कुल पृष्ठ का क्षेत्रफल एवं ब. आयतन निकालिए।
(1) 10 मी.,5 मी., 6 मी. (ii) 17 सेमी., 12 सेमी., 10 सेमी.
उत्तर—(i) कुल पृष्ठ का आयतन =l×b×h
= 10m×5m×6m = 300m³
(ii) कुल पृष्ठ का क्षे = 2(lb+ bh + hl)
=2(10×5+5×6+6×10)
= 2 (50+ 30+60)
2(140) = 280m³
(iii) कुल पृष्ठ का क्षे. =2(lb + bh + hl)
= 2(17×12+ 12×10+ 10×17)
= 2(204 + 120+ 170)
=2(494) = 988 m²
आयतन =l×b×h
= 17×12× 10=2040 cm³
3. 5 सेमी. किनारेवाले एक घन से 1 सेमी. किनारेवाले कितने घन काटे जा सकते हैं?
उत्तर—
घनों की सं• = 5 cm dysłu dkv kru/1cm dysłu dkv kru
= 5×5×5/1×1×1 = 125 cm²
4. एक घनाभ का आयतन 576 घनमीटर है और आधार वर्गाकार है जिसकी एक भुजा
6 मीटर है तो घनाभ की ऊँचाई ज्ञात कीजिए।
उत्तर— घनाभ का आयतन = lbh = 576
b=6m
l= 6m (आधार वर्गाकार है)
.: lbh =576
6×6×h =576
h= 576/6×6 = 16 m
5. 12 सेमी. किनारेवाले दो घन बराबर से जोड़ दिए जाएँ तो नए घनाभ का पृष्ठ क्षेत्रफल
ज्ञात कीजिए।
उत्तर—
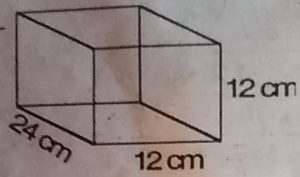
नए घनाभ में
h = 12 cm
b = 12 cm
l=24cm
पृष्ठ क्षे• = 2(lb + bh + lh)
=2 (24×12 + 12×12×24×12)
= 2 (288 + 144 +288)
=2×720 = 1440 m³
6. एक लड़का 2 लीटर दूध खरीदने गया। दुकानदार ने उसे एक आयताकार आधार वाले
बरतन से जो 20 सेमी. लम्बा, 15 सेमी. चौड़ा और 5 सेमी. गहरा था एक बार मापकर
दे दिया। बताइए उस लड़के को कितना कम या अधिक दूध मिला। (यदि 1 लीटर
= 1000 घन सेमी.)।
उत्तर— बरतन का आयतन =l×b×h
l= 20 cm
b = 15 cm
h = 5 cm
आयतन =20cm×15cm×5cm
=1500cm³
1 लीटर = 1000 cm³
दूध दिया = 1500 cm³
2 लीटर = 2000 cm³
दूध कम दिया = 2000—1500
=500 cm³ (आधा लीटर)
7. एक तालाब की लम्बाई 20 मीटर, चौड़ाई 12 मीटर और गहराई 8 मीटर है तथा एक
दूसरे तालाब की लम्बाई और चौड़ाई 20 मीटर के बराबर है तथा गहराई पहले तालाब
के बराबर है। किस तालाब में अधिक पानी अंटेगा?
उत्तर—पहले तालाब का आयतन = 20m × 12m × 8m = 1920 m³
दूसरे तालाब का आयतन = 20m²×8m = 160 m³
पहले तालाब में अधिक पानी अँटेगा।
8. एक खाली डिब्बा जिसमें साबुन रखा जाना है, डिब्बों की लम्बाई 0.40 मीटर, चौड़ाई
0.25 मीटर तथा ऊँचाई 0.25 मीटर है। साबुन 5 सेमी. × 4 सेमी. × 2 सेमी. साइज
का है। डिब्बा में कितने साबून रखे जा सकते हैं ?
उत्तर—डब्बों की l=0.40 m, b=0.25 m, h = 0.25 m
साबुन की l=5 cm, b =4cm, h = 2 cm
साबुनों की सं = 0.40 m × 0.25 m × 0.25 m/5 cm × 4 cm × 2 cm
= 40 cm × 25cm × 25cm/5cm × 4cm × 2cm
= 40×5×25/4×2 = 1000/8 = 125 साबुन
9. 30 मीटर लम्बा, 20 सेमी. चौड़ा तथा 4 मीटर ऊँची दीवार बनवानी है। यदि एक
ईंट की लम्बाई 25 सेमी., चौड़ाई 12.5 सेमी. तथा ऊँचाई 7.5 सेमी. हो तो उस दीवार
के बनवाने में कितने ईंट लगेंगी। (सीमेंट व बालू का आयतन नगण्य माना गया है।)
उत्तर—
दीवार का क्षे० =30m × 0.20 cm × 4m
ईंट की क्षे• = 25 cm × 12.5 cm × 7.5cm
= 30 ×.20 × 4/25 × 12.5 × 7.5
= 24m/2343.75cm
= 2400 m/234375cm
= 2400000/234375
= 10240 ईंटें।
10. एक कमरे की लम्बाई 15 मीटर, चौड़ाई 10 मीटर तथा ऊँचाई 8 मीटर है। उस घर
में कितनी हवा भरेगा?
उत्तर―
कमरे की लं० = 15 m
चौ• = 10 m
ऊँ• = 8m
कमरे का आयतन =l × b × h
= 15 m × 10 m × 8m = 1200 m³
■