BIHAR BOARD CLASS 9TH MATH | यक्लिड की ज्यामिति का परिचय
BIHAR BOARD CLASS 9TH MATH | यक्लिड की ज्यामिति का परिचय
Bihar Board Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry (युक्लिड के ज्यामिति का परिचय)
यक्लिड की ज्यामिति का परिचय
प्रश्नावली 5.1
1. निम्नलिखित कथनों में से कौन-से कथन सत्य हैं और कौन-से कञ्चन असत्य हैं? अपने उतारों के लिए कारण दीजिए।
(i) एक बिंदु से होकर केवल एक ही रेखा खींची जा सकती है।
(ii) दो भिन्न बिंदुओं से होकर जाने वाली असंख्य रेखाएँ हैं।
(iii) एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है।
(iv) यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
(v) आकृति 5.1 में, यदि AB = PQ और PQ= XY है, तो AB = XY होगा।
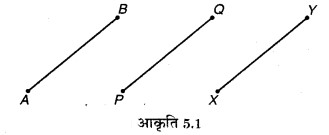
उत्तर:
(i) असत्य, हम एक बिन्दु से अनन्त रेखाएं लांच सकते है।
(ii) असत्य, दो भिन बिन्दुओं से केवल एक ही रेखा खींनी जा सकती है।
(iii) सत्य, बढ़ाई जा सकती है।
(iv) सत्य. दो बराबर चूतों की त्रिज्यार हमेश बराबर होती
(v) सत्य,
∴ AB = PQ = XY
अत: AB = XY
(ii) दो भिन्न बिंदुओं से होकर जाने वाली असंख्य रेखाएँ हैं।
(iii) एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है।
(iv) यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
(v) आकृति 5.1 में, यदि AB = PQ और PQ= XY है, तो AB = XY होगा।

उत्तर:
(i) असत्य, हम एक बिन्दु से अनन्त रेखाएं लांच सकते है।
(ii) असत्य, दो भिन बिन्दुओं से केवल एक ही रेखा खींनी जा सकती है।
(iii) सत्य, बढ़ाई जा सकती है।
(iv) सत्य. दो बराबर चूतों की त्रिज्यार हमेश बराबर होती
(v) सत्य,
∴ AB = PQ = XY
अत: AB = XY
2. निम्नलिखित पदों में से प्रत्येक की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद है, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इनें कैसे परिभाषित कर पाएंगे?
(i) समांतर रेखाएँ
(ii) लम्ब रेखाएँ
(i) रेखाखंड
(iv) वृत्त की त्रिज्या
(v) वर्ग।
उत्तर:
(i) यदि दो रेखाएँ आपस में कभी प्रतिच्छेद न करें तो वह समांतर रेखार होती हैं।
(ii) यदि दो रेखाएँ एक दूसरे को केवल एक ही समकोण पर प्रतिक्छेद करती है तो वे लम्ब रेखाएँ होती हैं।
(iii) यदि हम एक रेखा पर दो बिन्दु लेते हैं तो दोनों बिन्दुओं के मध्य भाग को रेखाखंड कहते हैं।
(iv) वृत्त के केन्द्र से उसकी परिधि के बीच की दूरी त्रिज्या कहलाती है।
(v) वह चतुर्भुज जिसकी चारों भुजाएँ बराबर हों तथा प्रत्येक कोण समकोण हो, वर्ग कहलाता है।
इनमें प्रयोग हुए पद हम पहले ही पड़ चुके है अतः इन्हें परिभाषित करने की आवश्यकता नहीं है। यदि किसी विद्यार्थी को कोई पद नहाँ जात है तो वह अपने सहपाठी से चर्चा करके जात करे।
(ii) लम्ब रेखाएँ
(i) रेखाखंड
(iv) वृत्त की त्रिज्या
(v) वर्ग।
उत्तर:
(i) यदि दो रेखाएँ आपस में कभी प्रतिच्छेद न करें तो वह समांतर रेखार होती हैं।
(ii) यदि दो रेखाएँ एक दूसरे को केवल एक ही समकोण पर प्रतिक्छेद करती है तो वे लम्ब रेखाएँ होती हैं।
(iii) यदि हम एक रेखा पर दो बिन्दु लेते हैं तो दोनों बिन्दुओं के मध्य भाग को रेखाखंड कहते हैं।
(iv) वृत्त के केन्द्र से उसकी परिधि के बीच की दूरी त्रिज्या कहलाती है।
(v) वह चतुर्भुज जिसकी चारों भुजाएँ बराबर हों तथा प्रत्येक कोण समकोण हो, वर्ग कहलाता है।
इनमें प्रयोग हुए पद हम पहले ही पड़ चुके है अतः इन्हें परिभाषित करने की आवश्यकता नहीं है। यदि किसी विद्यार्थी को कोई पद नहाँ जात है तो वह अपने सहपाठी से चर्चा करके जात करे।
3. नीचे दी गई दो अभिधारणाओं पर विचार कीजिए :
(i) दो भिन्न बिंदु A बिंदु B दिए रहने पर, एक तीसरा बिंदु C ऐसा विद्यमान है
जो A और B के बीच स्थित होता है।
(ii) यहाँ कम-से-कम ऐसे तीन बिंदु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं।
क्या इन अभिधारणाओं में कोई अपरिभाषित शब्द हैं ? क्या ये अभिधारणाएँ
अविरोधी हैं ? क्या ये यक्लिड की अभिधारणाओं से प्राप्त होती हैं ? स्पष्ट कीजिए।
हल : यहाँ पर बहुत सारे अपरिभाषित पद हैं जिनको विद्यार्थी स्वयं लिखें। ये संगत हैं
क्योंकि ये दो विभिन्न परिस्थितियों में Deal करते हैं।
(i) कहें, दो बिंदु A तथा B दिए गए हैं, वहाँ पर C एक बिंदु है जो उनके बीच रेखा
पर स्थित है।
(ii) कहें, A तथा B दिए गए हैं, हम एक बिंदु C ले सकते हैं, जो A तथा B से होकर
गुजरती हुई रेखा पर स्थित नहीं हैं।
यह अभिगृहीत यूक्लिड के अभिगृहीतों पर आधारित नहीं है। हालांकि ये अभिगृहीतों का
अनुसरण करते हैं । क्योंक दो दिए हुए विभिन्न बिंदुओं से केवल एक ही रेखा गुजर सकती है।
4. यदि दो बिंदुओं A और B के बीच एक बिंदु C एसा स्थित है कि AC = BC है, तो सिद्ध कीजिए कि AC= 1/2 AB है। एक आकृति खींच कर इसे स्पष्ट कीजिए ।
हल : हमारे पास एक बिंदु C है जो कि दो बिंदुओं A तथा B के बीच में इस प्रकार स्थित
है कि AC = BC

दोनों ओर AC जोड़ने पर, AC+ AC = AC+ BC.
या, 2AC = AB[चूंकि AC+CB, AB के सम्पाती हैं]
.: AC =1/2AB
5. प्रश्न 4 में, रेखाखंड AB का मध्य-बिंदु कहलाता है। सिद्ध कीजिए कि एक
रेखाखंड का एक और केवल एक ही मध्य-बिंदु होता है।
हल : माना कि AB का D एक ओर मध्य बिंदु है।
.: AD = DB …..(1)
लेकिन दिया गया है कि C,AB का मध्य बिंदु है।
.: AC = CB …..(2)
(1) को (2) में से घटाने पर, AC-AD=CB – DB
या, DC = – DC
या, 2DC = 0 या, DC = 0

C तथा D सम्पाती हैं।
इस प्रकार, हर एक रेखाखंड का केवल एक ही मध्य बिंदु होता है।
6. आकृति में यदि AC = BD है,
तो सिद्ध कीजिए कि AB = CD है।
हल: AC = BD ….(1)
[दिया है]
तथा AC=AB+ BC …(2)
[बिंदु B,A तथा C के बीच में स्थित है।
और BD = BC+CD….(3) [बिंदु C, B तथा D के बीच में स्थित है।

AC और BD का मान समीकरण (2) और (3) से समीकरण (1) में प्रतिष्ठापित करने पर,
AB + BC = BC + CD या, AB + BC – BC = BC + CD – BC
या, AB = CD
7. यूक्लिड की अभिगृहीतों की सूची में दिया हुआ अभिगृहीत 5 एक सर्वव्यापी सत्य क्यों माना जाता है ? (ध्यान दीजिए कि यह प्रश्न पाँचवीं अभिधारणा से संबंधित नहीं है।)
हल : यूक्लिड की अभिगृहीतों की सूची में दिया हुआ अभिगृहीत 5 ब्रह्मांड की किसी भी चीज के लिए सत्य है। अतः यह सदैव सत्य है।
प्रश्नावली 5.2
1. आप यूक्लिड की पांचवीं अभिधारणा को किस प्रकार लिखेंगे ताकि वह सरलता से समझी जा सके?
हल : अभिगृहीत 2 तथ्यों का प्रयास:
(i) P से गुजरती हुई एक रेखा है जो कि l के समांतर है।
(ii) ऐसी केवल एक ही रेखा है।
2. क्या यूक्लिड की पांचवीं अभिधारणा से समांतर रेखाओं के अस्तित्व का औचित्य निर्धारित होता है ? स्पष्ट कीजिए।
हल : यदि एक सीधी रेखा l, दो सीधी रेखाओं m तथा n पर इस प्रकार मिलती हैं कि आंतरिक कोणों का योग दो समकोण, l भुजा के एक ओर हो तो यूक्लिड के पाँचवें अभिगृहीत के अनुसार रेखाएँ l के इस ओर नहीं मिलेंगी।
हम जानते हैं कि l के दूसरी और आंतरिक कोणों का योग भी दो समकोण होगा। इसलिए वे रेखाएँ इस ओर भी वहीं मिलेंगी। अतः ये कभी भी नहीं मिलेंगी। इसलिए ये समांतर हैं।
●
