bseb class 11 economics | आँकड़ों का प्रस्तुतीकरण

                 ( Presentation of Data )

पाठ्यक्रम (Syllabus)

• सारणी के द्वारा अंकों का प्रस्तुतीकरण ।

•विभिन्न चित्रों के माध्यम से आँकड़ों का प्रदर्शन ।

” याद रखने योग्य बातें (Points to Remember):-

1. आँकड़ों का वर्णनात्मक प्रस्तुतीकरण (Textual or Descriptive Presentation)- आँकड़ों का वर्णनात्मक प्रस्तुतीकरण तब किया जाता है जब आँकड़ों की मात्रा बहुत अधिक नहीं होनी । उदाहरण के लिये 5 मार्च, 2007 को तेल वह डीजल की बढ़ती हुई कीमतों के विरुद्ध बंद का आह्वान किया गया। इस दिन 17 पेट्रोल पम्प बंद तथा 5 खुले पाए गए।

2. आँकड़ों का तालिका के रूप में प्रस्तुतीकरण (Tabular Presentation of Data)-तालिका में आँकड़ों को पक्तियों (Rows) तथा स्तभों में व्यवस्थित रूप से क्रमबद्ध किया जाता है। तालिका में जो वर्गीकरण प्रयोग में लाया जाता है, वह चार प्रकार का होता है-

(i) गुणात्मक, (ii) परिमाणात्मक, (iii) समायानुसार तथा, (iv) स्थानानुसार ।

(i) गुणात्मक वर्गीकरण (Qualitative Classification)- इस विधि में मात्रा या माप के आधार पर आँकड़ों का वर्गीकरण किया जाता है।

(ii) परिमाणात्मक वर्गीकरण-इस विधि में मात्रा या माप के आधार पर आंकड़ों के वर्गीकरण किया जाता है।

(iii) समायानुसार वर्गीकरण (Temporial Classification)- इस विधि में चरों या आँकड़ों का वर्गीकरण समयानुसार किया जाता है। समय घंटों, दिनों, सप्ताहों, महीनों, वर्षों आदि में हो सकता है।

(iv) स्थान संबंधी या स्थानिक वर्गीकरण-गाँवों, शहरों, जिलों आदि के आधार पर आँकड़ों के वर्गीकरण को स्थान संबंधी वर्गीकरण कहते हैं।

आँकड़ों का सारणीयन तथा सारणी के भाग (Tabulation of Data and parts of a table)-आँकड़ों को पंक्तियों तथा स्तम्भों में व्यवस्थित रूप से क्रमबद्ध करने की क्रिया को सारणीयन कहते हैं। एक अच्छी सारणी के मुख्य भाग निम्नलिखित हैं-

(i) सारणी संख्या (Table Number)-सारणी की पहचान के लिए उसे एक संख्या दी जाती है। यह संख्या शीर्षक के ऊपर या सारणी के आरंभ में दी जाती है।

(ii) शीर्षक (Title)-हर सारणी के ऊपर शीर्षक लिखा जाना चाहिए। यह शीर्षक सरल, संक्षिप्त और स्पष्ट होना चाहिये । शीर्षक सारणी संख्या के नीचे लिखा जाना चाहिए।

(iii) उपशीर्षक और स्तंभ शीर्षक (Caption and Stubs)-खाने के शीर्षक को उपशीर्षक और स्तंभों के शीर्ष को स्तंभशीर्षक (Stubs) कहते हैं।

(iv) सारणी का मुख्य भाग या कलेवर (Body)-कलेवर सारणी का एक महत्त्वपूर्ण भाग है। सारी सूचनाएँ इस भाग में प्रस्तुत की जाती हैं।

(v) स्त्रोत (Source)-सारणी के अंत में नीचे बाईं ओर आँकड़ों के स्रोत का उल्लेख किया जाता है।

(vi) पाद टिप्पणियाँ (Foot Notes)-सारणी में दिए गए समंकों और शब्दों को स्पष्ट करेन के लिए कभी-कभी पाद टिप्पणियाँ आवश्यक होती हैं

(3) आँकड़ों का आरेखीय प्रस्तुतीकरण (Diagrammatic Presentatioin of Data)-यह आँकड़ों के प्रस्तुतीकरण करने की तीसरी विधि है । रेखा आरेख किसी जटिल स्थिति के स्वरूप को दिखाने में हमारी सहायता करते हैं। आंकड़ों के रेखीय प्रदर्शन से आँकड़ों के विश्लेषण और तुलना में बहुत सहायता मिलती है । रेखा आरेख कई प्रकार के होते हैं। उनमें तीन मुख्य हैं-

(i) ज्यामितीय रेखा आरेख, (ii) आवृत्ति रेखा आरेख तथा (iii) गणितीय रेखा आरेख ।

ज्यामितीय रेखा आरेखों में दंड आरेख (Bar diagram) तथा वृत्त आरेख (Pie-diagram) आते हैं । दंड आरेख तीन प्रकार के होते हैं-(i) साधारण दंड आरेख तथा

(ii) बहुदण्ड आरेख तथा (iii) घटक दंड आरेख ।

(i) साधारण दंड आरेख (Simple Bar Diagram)-सरल दण्ड द्वारा केवल एक ही चर को प्रदर्शित किया जा सकता है। जैसे विभिन्न वर्षों का चीनी उत्पादन, सार्वजनिक व्यय की राशि आदि । किसी चर के मूल्यों को आयत (जिन्हें दण्ड कहते हैं) के माध्यम से व्यक्त किया जाता है। आयत की लम्बाई मद के मूल्य को व्यक्त करती है। आयत या दंड की चौड़ाई केवल आरेख की सुंदरता के लिए होती है। सरल दंड आरेख आवृत्ति वाले तथा न आवृत्ति वाले दोनों आँकड़ों तथा गुणों के लिए उपयुक्त है।

(ii) बहुदंड आरेख (Multiple Bar Diagram)-विभिन्न वर्षों के एक से अधिक चरों के मूल्यों को बहुदंड आरेख द्वारा प्रदर्शित किया जाता है जैसे-स्त्रियों और पुरुषों की

संख्या, आयात और निर्यात मूल्य आदि ।

(iii) घटक दंड आरेख (Component Bar Diagram)- तथ्यों के जोड़ और उसके विभिन्न विभागों (जैसे खाद्यान्नों का उत्पादन और उसके विभिन्न भागों का उत्पादन जैसे-चावल, गेहूँ, दालें आदि) का प्रदर्शन करना होता है तो घटक दंड आरेख का प्रयोग किया जाता है। इसी प्रकार यदि विभिन्न वर्षों में एक कॉलेज में लड़के और लड़कियों की संख्या अलग-अलग करके दिखानी है तो घटक दंड आरेख का प्रयोग किया जाता है। घट दंड आरेखों में उपयुक्त रंग या छाया भरे जाते हैं।

वृत्त आरेख (Pie-Diagram)-वृत्त आरेख किसी भी तथ्य को जोड़ के विभिन्न भागों की सापेक्षिक स्थिति (प्रतिशत भाग) को प्रस्तुत करने का एक बहुत सरल और आकर्षक तरीका है। इसके अंतर्गत एक वृत्त के विभिन्न खंडों की सहायता से किसी भी तथ्य के विभिन्न मूल्यों का सापेक्षिक भाग को प्रदर्शित किया जाता है। इसे वृत्त आरेख इसलिए कहते हैं, क्योंकि सारा आरेख एक वृत्त की तरह लगता है और इसके घटक वृत्त के टुकड़ों के अनुरूप होते हैं।

आवृत्ति या बारंबारता आरेख (Frequency Diagram)- बारम्बारता वितरण के रूप में प्रस्तुत आँकड़ों में आयत चित्र, आवृत्ति बहुभुज, आवृत्ति वक्र तथा तोरण (Ogive) आते हैं।

(i) आयत चित्र (Histogram)-आयत चित्र अखंडित श्रृंखला को प्रस्तुत करने का सबसे उत्तम व प्रचलित तरीका है। आयत चित्र के अन्तर्गत वितरण की वर्ग

आवृत्तियों को खड़े हुए आयतों की पंक्तियों के रूप में प्रस्तुत किया जाता है । ये आयत आपस में जुड़े होते हैं।

(ii) आवृत्ति बहुभुज (Frequency Polygon)-आवृत्ति बहुभुज आयत चित्र का वैकिल्पक रूप है और यह प्राय: आयत चित्र की सहायता से बनाया जाता है। आवृत्ति

बहुभुज बनाने का सरल तरीका आयत चित्र को बंधी हुई आयतों के ऊपरी मध्य बिन्दुओं को मिलना है।

(iii) आवृत्ति वक्र (Frequency Curve)-यह आवृत्ति बहुभुज का सरल रूप है । मुक्त हस्त (Free hand) द्वारा आवृत्ति बहुभुज की कोणीयता को इस ढंग से समाप्त किया जाता है कि इसका क्षेत्रफल पहले जितना ही रहे । वक्र के दोनों सिरे भुजाक्ष से मिला दिए जाते हैं।

(iv) तोरण (Ogive)-तोरण को संचयी आवृत्ति वक्र भी कहते हैं । तोरण दो प्रकार की होते हैं-‘से कम’ तथा ‘से अधिक’ | ‘से कम’ तोरण नीचे से ऊपर दाईं ओर उठता

है और ‘से अधिक’ तोरण ऊपर से नीचे दाईं ओर ढालू होता है। संचयी आवृत्ति वक्रों की सहायता से हम विभिन्न मूल्यों को ज्ञात कर सकते हैं-जैसे माध्यिका, चतुर्थक, दशमे, शतमक।

गणितीय रेखा आरेख (Arithmatic Line Graph)-इसे काल श्रेणी आलेख भी कहते हैं। इस चित्र में समय (घंटे, दिन/तिथि, सप्ताह, मास, वर्ष इत्यादि) को x-अक्ष पर दिखाया जाता है और चरों के मानों को y-अक्ष पर दिखाया जाता है।

पाठ्यपुस्तक एवं परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्नोत्तर

(Textbook and Other Important Questions for Examination)

                     अति लघु उत्तरीय प्रश्न

         (Very Short Answer Type Questions)

प्रश्न 1. सारणीयन में प्रयोग किया जाने वाला वर्गीकरण कितने प्रकार का होता हैं ?

उत्तर-चार प्रकार का-(i) परिमाणात्मक, (ii) गुणात्मक, (ii) समय संबंधी तथा (iv) स्थान संबंधी।

प्रश्न 2. परिमाणात्मक या मात्रात्मक वर्गीकरण किसे कहते हैं?

उत्तर-परिमाणात्मक वर्गीकरण उस वर्गीकरण को कहते हैं, जिसमें वर्गीकरण का आधार परिमाणात्मक विशेषताएँ हैं। दूसरे शब्दों में इन विशेषताओं को मात्रा में मापा जा सकता है। उदाहरण के लिए आयु, ऊँचाई, उत्पादन, आय आदि मात्रात्मक विशेषताएँ हैं।

प्रश्न 3. सारणी का मुख्य भाग कौन-सा है ?

उत्तर-सारणी का मुख्य भाग कलेवर (Body) है।

प्रश्न 4. आँकड़ों को दर्शाने के लिए मुख्य आरेख निम्नलिखित हैं-

उत्तर-(i) ज्यामितीय आरेख (Geometric diagram)। जैसे-दंडभुज ।

(ii) आवृत्ति आरेख (Frequency diagram) |

(iii) गणितीय रेखा आरेख (Arithmatic Line graph) |

प्रश्न 5. सांख्यिकीय सारणी क्या है?

उत्तर-सांख्यिकीय सारणी एक संयंत्र है जिसमें आँकड़ों को पंक्तियों और स्तम्भों में व्यवस्थित ढंग से प्रस्तुत किया जाता है।

प्रश्न 6. सारणीयन किसे कहते हैं?

उत्तर-सांख्यिकीय आँकड़ों को सारणी के रूप में अर्थात् पंक्तियों तथा स्तंभों के रूप में प्रकट करने को सारणीयन कहते हैं।

प्रश्न 7. सारणीयन के कोई दो उद्देश्य लिखिए।

उत्तर-(i) आँकड़ों को क्रमबद्ध और सुव्यवस्थित ढंग से प्रस्तुत करना ।

(ii) आंकड़ों का सरलीकरण करना ।

प्रश्न 8. वर्गीकरण तथा सारणीयन में कोई एक अंतर बताएँ।

उत्तर-वर्गीकरण सांख्यिकी विश्लेषण की एक विधि है जब कि सारणीयन समंकों को प्रस्तुत करने की एक विधि है।

प्रश्न 9. सारणी के कोई पाँच प्रमुख अंग लिखें।

उत्तर-(i) सारणीयन संख्या, (ii) शीर्षक, (iii) शीर्ष टिप्पणी, (iv) उप-शीर्षक व पंक्तिशीर्षक,

(iv) सारणी का मुख्य भाग । (v) सारणी का मुख्य भाग ।

प्रश्न 10. यदि सारणी में एक निश्चित संख्या को महत्त्व दिया जाना है तो क्या करना चाहिए?

उत्तर-विशेष महत्त्व वाले समंकों को मोटे अंकों में लिखा जाना चाहिए।

प्रश्न 11. सरल सारणी से क्या अभिप्राय है?

उत्तर-सरल सारणी वह सारणी है जो सांख्यिकीय आँकड़ों की किसी एक विशेषता अथवा गुण को प्रदर्शित करती है।

प्रश्न 12. जटिल सारणी किसे कहते हैं ?

उत्तर-जटिल सारणी उस सारणी को कहते हैं जो कि एक से अधिक विशेषताओं को दर्शाती है।

प्रश्न 13. स्तंभों के शीर्षक को क्या कहा जाता है?

उत्तर-स्तंभों के शीर्षक को उप-शीर्षक कहते हैं।

प्रश्न 14. आरेखीय प्रदर्शन से क्या अभिप्राय है ?

उत्तर-आरेखीय प्रदर्शन वह विधि है जिसके द्वारा आँकड़ों को आरेखों (दंड आरेख, आयत चित्र, वृत्तीय आरेख) द्वारा प्रस्तुत किया जाता है।

प्रश्न 15. आरेखों की कोई दो सीमाएँ लिखो।

उत्तर-(i) आरेख अनुमानों पर आधारित होते हैं।

(ii) ये विस्तृत जानकारी नहीं देते ।

प्रश्न 16. आरेखों के कोई दो लाभ लिखें।

उत्तर-(i) आरेखों द्वारा आँकड़ों की प्रस्तुति मितव्ययी होती है।

(ii) इनका व्यापक प्रयोग होता है।

प्रश्न 17. सरल दंड आरेख पर टिप्पणी लिखें।

उत्तर-सरज दंड आरेखों में मूल्यों को दंडों की ऊंचाई द्वारा दिखाया जाता है। दण्डों की पीटाई तथा उनके बीच की दूरी एक समान रखी जाती है। ये आरेख जनसंख्या, उत्पादन तथा भौगोलिक आँकड़ों को प्रदर्शित करने में उपयोगी होते हैं।

प्रश्न 18. सूचना के स्रोत से क्या अभिप्राय है?

उत्तर-सूचना के स्रोत से अभिप्राय उस स्रोत से है जिससे आँकड़े लिए गए हैं।

प्रश्न 19. बहुभुजी सारणी किसे कहते हैं ?

उत्तर-दो गुणों से अधिक विशेषताओं के आधार पर निर्मित की गई सारणी को बहुभुजी सारणी कहते हैं।

प्रश्न 20. एक अच्छी सांख्यिकीय सारणी की कोई तीन विशेषताएँ लिखें।

“उत्तर-(i) यह सरल तथा संक्षिप्त होनी चाहिए, (ii) स्पष्ट तथा देखने में आकर्षक होनी चाहिए, (ii) विश्वसनीय होनी चाहिए।

प्रश्न 21. निम्नलिखित को प्रस्तुत करने के लिए किस प्रकार का आरेख अधिक प्रभावशाली है?

(i) वर्ष विशेष की मासिक वर्षा ।

(ii) धर्म के अनुसार दिल्ली की जनसंख्या का संघटन।

(iii) एक कारखाने में लागत-घटक

उत्तर-(i) काल श्रेणी आरेख । (ii) सरल दण्ड आरेख तथा (iii) वृत्त आरेख ।

प्रश्न 22. जब वर्गान्तर असमान हैं तो आयत चित्र की ऊंचाई कैसे निर्धारित की जाती है?

उत्तर-सबसे कम वर्गान्तर से वर्गान्तर जितना अधिक होगा, आयत की ऊंचाई के लिए उस वर्गान्तर की आवृत्ति उसी अनुपात से कम कर दी जाती है। मान लो एक वर्गान्तर न्यूनतम वर्गान्तर का दोगुना है तो ऐसी अवस्था में उसके आयत की ऊंचाई आधी कर दी जाएगी। अर्थात् उसकी आवृत्तियाँ 6 हैं तो वह 3 (6 +2) होंगी।

प्रश्न 23. संचयी आवृत्ति के कितने रूप हो सकते हैं ?

उत्तर-संचयी आवृत्ति के दो रूप हो सकते हैं-(i) ‘ से कम’ तथा ‘से अधिक’ । ‘से कम’ ओजाइन नीचे से ऊपर दाईं ओर उठती है और ‘से अधिक’ ओजाइब ऊपर से नीचे की ओर दाई ओर ढालू होती है।

प्रश्न 24. आयत चित्र बनाने के लिए समावेशी पर आधारित श्रृंखला को अपवर्जी वर्ग पर आधारित श्रृंखला में क्यों परिवर्तित करते हैं ?

उत्तर-समावेशी वर्ग पर आधारित श्रृंखला में अंतर होता है और आवृत्ति चित्र बनाने के लिये निरन्तरता चाहिए। अतः निरन्तरता प्राप्त करने के लिए हम समावेशी वर्ग पर आधारित श्रृंखला को अपवर्जी वर्ग पर आधारित श्रृंखला में परिवर्तित करते हैं।

प्रश्न 25. ओजाइब का दूसरा नाम क्या है ?

उत्तर-ओजाइब का दूसरा नाम संचयी आवृत्ति वक्र या तोरण है।

प्रश्न 26. दोनों ओजाइब की विशेष विशेषता क्या है?

उत्तर-दोनों ओजाइब जिस बिन्दु पर एक दूसरे को काटते हैं उस बिन्दु से हमें माध्यिका प्राप्त होती है।

प्रश्न 27.सरल दंड आरेख द्वारा कितने चरों को प्रदर्शित किया जा सकता है?

उत्तर-सरल दंड आरेख द्वारा केवल एक ही चर को प्रदर्शित किया जा सकता है।

प्रश्न 28. किस प्रकार के दंड आरेख का हमें प्रयोग करना होगा, यदि हमें विभिन्न वर्षों के एक से अधिक चरों के मूल को प्रदर्शित करना हो तो?

उत्तर-बहुदंड आरेख को।

प्रश्न 29. हमें एक देश के आयात तथा निर्यात के मूल्यों को दंड आरेख द्वारा प्रदर्शित करना है। इसके लिये हम किस प्रकार के दंड आरेख का प्रयोग करेंगे?

उत्तर-बहुदंड आरेख का।

प्रश्न 30.एक उदाहरण दीजिए जहाँ सरल दंड आरेख का प्रयोग किया जा सकता है।

उत्तर-जब विभिन्न जनगणना वर्षों में एक ही राज्य की जनसंख्या प्रदर्शित करनी हो।

प्रश्न 31. सरल दंड आरेख तथा बहुदंड आरेख में एक अन्तर बताएँ।

उत्तर-सरल दंड आरेख में एक ही चर के मूल्यों को विभिन्न वर्षों में व्यक्त किया जाता है। जबकि बहु दंड आरेख में एक से अधिक चर के मूल्यों को प्रदर्शित किया जाता है।

प्रश्न 32. समय कालिक श्रृंखला किसे कहते हैं ?

उत्तर-समय कालिकशृंखला वह श्रृंखला है जहाँ किसी चर का मूल्य समयानुसार दिया हो, जैसे विभिन्न वर्षों के कृषि उत्पादन के आंकड़े।

प्रश्न 33. आयत चित्र का अर्थ बताएं।

उत्तर-यह वह चित्र है जो अखंडित श्रृंखलाओं से जुड़ी हुई आयतों (adjacent rectangles) द्वारा प्रदर्शित करता है।

प्रश्न 34. यदि सभी वर्ग अंतराल (Class Intervals) समान हैं तो आयत चित्र की चौड़ाई समान होगी या असमान?

उत्तर-समान होगी।

प्रश्न 35. आवृत्ति बहुभुज कैसे बनाया जाता है ?

उत्तर-आवृत्ति बहुभुज को आयत चित्र के सिरे के मध्य बिन्दुओं को जोड़कर बनाया जाता है।

प्रश्न 36. श्रम पर खर्च कुल खर्चे का 30% है । इसकी कोण की डिग्री बताएँ।

उत्तर-कोण की डिग्री = 30×3.6 = 108⁰

प्रश्न 37. 102 मजदूरों में मुख्य मजदूर 31 हैं । मुख्य मजदूरों की कोण की डिग्री बताएँ।

उत्तर-कोण की डिग्री = 31/102 x360 = 1090

प्रश्न 38. दो तोरण (ogive) से कम और ‘से अधिक’ एक दूसरे को M बिन्दु पर काटते हैं । माध्यिका (Median) निकालने के लिए क्या करना चाहिए?

उत्तर-माध्यिका निकालने के लिए Mबिन्दु से आधार रेखा पर लंब डालना चाहिए। आधार बिन्दु आधार रेखा को जिस बिन्दु पर काटेगा, वह बिन्दु माध्यिका प्रदर्शित करेगा।

                    लघु उत्तरीय प्रश्न

        (Short Answer Type Questions)

प्रश्न 1. वृत्त आरेख बनाने की विधि लिखें।

(Write down the method of constructing pie diagram.)

उत्तर-वृत्त आरेख बनाने की विधि (Method of constructing a pie diagram)-

(i) प्रत्येक दिए गए मूल्य को कुल मूल्य के प्रतिशत रूप में परिवर्तित किया जाता है। यदि मूल्य पहले से ही प्रतिशत में दिया गया है तो यह चरण छोड़ दिया जाता है

(ii) प्रतिशत मूल्य को 3.6 से गुणा करके उस मूल्य का कोण ज्ञात किया जाता है। ।

(iii) पेंसिल और परकार की सहाययता से एक उचित वृत बनाया जाता है।

(iv) वृत्त में प्रत्येक मद का कोण बनाया जाता है।

(v) वृत्त आरेख के प्रत्येक खंड में अलग-अलग रंग भरे जाते हैं।

(vi) वृत्त आरेख के प्रत्येक खंड में अलग-अलग रंग भरा जाता है।

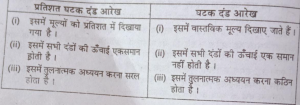
प्रश्न 2. प्रतिशत घटक दंड आरेख तथा घटक दंड आरेख में अन्तर बताएँ।

(Differentiate between percentage component bar digram and diagram.)

उत्तर-प्रतिशत घटक दंडआरेख तथा घटक दंड आरेख में अंतर

प्रश्न 3. आँकड़ों के आरेखीय प्रस्तुतीकरण के लाभ लिखें।

(Write down the advantages of diagrammatic presentation of data)-

उत्तर – आंकड़ों के आरेखीय प्रस्तुतीकरण के लाभ (Advantages of diagrammatic presentation of data)

(i) आरेख आँकड़ों को प्रस्तुत करने का एक प्रभावशाली साधन हैं, क्योंकि आरेख रोचक तथा आकर्षक होते हैं।

(ii) आरेख आंकड़ों को सरल तथा बोधगम्य बनाते हैं।

(iii) ये समकों के तुलनात्मक अध्ययन में सहायक होते हैं।

(iv) इनका प्रयोग उत्पादन, व्यापार, वाणिज्य, परिवहन आदि के क्षेत्र में बहुत उपयोगी है।

प्रश्न 4. दंड आरेख की विशेषताएं लिखें।

(Write down the features of bar-diagram.)

उत्तर – विशेषताएं (Features)-

(i) दंड आरेख एकपक्षीय (One Dimensional) होते हैं।

(ii) दंड क्षैतिज (Horizontal) तथा शीर्ष (Vertical) दोनों रूप में हो सकते हैं।

(iii) दंड आरेखों को आकर्षक बनाने के लिए सभी दंडों में रंग भर दिया जाता है।

(iv) दंड आरेख कई प्रकार के होते हैं-जैसे सरल एंड आरेख, बहु दंड आरेख, घटक दंड आरेख, प्रतिशत घटक दंड आरेख आदि।

प्रश्न 5. परिमाणात्मक वर्गीकरण का एक उदाहरण दें।

(Give an example of quantitative classification.)

उत्तर-

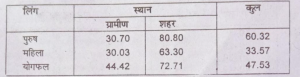
प्रश्न 6. गुणात्मक वर्गीकरण का एक उदाहरण दें।

(Give an example of quantitative classification.)

उत्तर – बिहार में साक्षरता (प्रतिशत में) (Literacy in Bihar in Percentage)

प्रश्न 7. समयानुसार या कालिक वर्गीकरण का एक उदाहरण दें।

(Give an example of temporal classification.)

उत्तर – 1995-2000 में एक चाय की दुकान की वार्षिक विक्री-

प्रश्न 8. स्थानिक वर्गीकरण का एक उदाहरण दें।

(Give an example of the spatial classification.)

प्रश्न 9. घटक दण्ड आरेख का प्रयोग कब किया जाता है ? इस आरेख को बनाने की विधि लिखें।

(When is component bar diagram prepared ? Write down the method of preparing it.)

उत्तर-जब तथ्यों के जोड़ और उसके विभिन्न विभागों (जैसे-कॉलेज के विद्यार्थियों और उसके विभिन्न घटकों की संख्या जैसे लड़के तथा लड़कियों आदि) का प्रदर्शन करना हो तो घटक दण्ड आरेख का प्रयोग किया जाता है।

बनाने की विधि (Method of preparing)-पहले समय अथवा स्थान के आधार पर, तथ्यों के जोड़ के आधार दंड बनाए जाते हैं। बाद में प्रत्येक खंड के विभिन्न भागों में अलग-अलग रंग भरा जाता है परन्तु एक वस्तु से संबंधित सभी दंडों के भागों में एक ही रंग भरा जाता है।

प्रश्न 10. निम्नलिखित आवृत्ति वितरण से हम एक आयत चित्र बनाना चाहते हैं । ऐसा करने के लिए हम वर्गान्तर में क्या परिवर्तन करेंगे?

(We have to draw a histogram with the help of following data. What amendment will we make in class intervals for doing so ?)

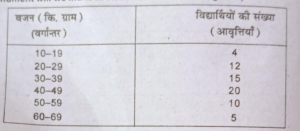
उत्तर-

प्रश्न 11. प्रतिशत घटक दंड आरेख बनाने की विधि में निहित चरण लिखें।

(Write down the steps involved in the construction of percentage component bar diagram.)

उत्तर – प्रतिशत घटक दंड आरेख बनाने की विधि में निम्नलिखित चरण होते हैं-

(i) इन्हें बनाने के लिए पहले सभी समय (वर्षों आदि) से सम्बन्धित जोड़ को 100 मान लिया जाता है।

(ii) दूसरे, सभी विभागों को प्रतिशत रूप में बदल दिया जाता है।

(iii) चौथे, अलग-अलग समय (वर्षों) के अलग-अलग दंड बनाए जाते हैं, जिनकी ऊंचाई समान अथवा 100 होती है। फिर बाद में संचयी प्रतिशत के बराबर विभिन्न विभागों को काट दिया जाता है और उनमें अलग-अलग रंग भर दिया जाता है।

प्रश्न 12. वृत्त आरेख बनाने की विधि लिखें।

(Write down the method of constructing pie diagram.)

उत्तर – वृत्त आरेख की विधि के चरण इस प्रकार हैं-

(i) प्रत्येक दिए गए मूल्य को कुल मूल्य के प्रतिशत में परिवर्तित किया जाता है। यदि मूल्य पहले से ही प्रतिशत में हो तब यह चरण छोड़ दिया जाता है।

(ii) प्रतिशत मूल्य को 36 से गुण करके उस मूल्य का कोण ज्ञात किया जाता है ।

(iii) पंसिल और परकार की सहायता से एक उचित वृत्त का निर्माण किया जाता है।

(iv) वृत्त में प्रत्येक मद का कोण बनाया जाता है।

(v) वृत्त आरेख के प्रत्येक खंड में अलग-अलग रंग भरे जाते हैं।

प्रश्न 13. सामान्य प्रयोग में लाए जाने वाले आरेखों के विभिन्न रूप लिखें।

(Write down the various kinds of diagrams in common use.)

उत्तर – सामान्य प्रयोग में लाए जानेवाले आरेखों के विभिन्न रूप निम्नलिखित हैं-

(i) ज्यामितीय आरेख (Geometric diagrams)-(i) दंड आरेख, (ii) बहुदंड आरेख, (iii) वृत्तीय आरेख।

(ii) आवृत्ति आरेख (Frequency diagrams)-(i) आयत चित्र, (ii) आवृत्ति बहुभुज,(iii) आवृत्ति वक्र तथा  (iv) तोरण ।

(iii) गणितीय समय ग्राफ (Arithmetic Time Graph)-काल श्रेणी आरेख ।

प्रश्न 14. सामान्य उद्देश्य सारणी तथा विशेष उद्देश्य सारणी में अन्तर बताएँ।

(Differentiate between general purpose table and special purpose table.)

उत्तर-सामान्य उद्देश्य सारणी का कोई महत्त्व नहीं होता। ये सामान्यत: प्रकाशित प्रतिवेदनों (Report) के पीछे दी जाती है। विभिन्न व्यक्ति इसका प्रयोग अपने ढंग से करते हैं। इसके *******विशेष उद्देश्य सारणी किसी विशेष उद्देश्य की पूर्ति के लिए बनाई गई होती है। यह प्राय: ****** होती है।

प्रश्न 15 अविछिन्न तथा खंडित (विछिन्न ) चरों में अन्तर बताएँ । उदाहरण देकर समझएं।

(Distinguish between : (a) Continuous and (b) Discrete variables. Explain with examples.)

उत्तर – अविछिन्न तथा विछिन्न चरों में अन्तर (Difference between Continuous Series)- एक चर को विभिन्न चर उस समय कहा जाता है जब वह विस्तार में कोई भी मूल्य ले सकता है। उसका मूल्य 1.2, 3 भी हो सकता है और

1/2, 1/3, 3/4, 7/8 अथवा √2 या 1- 414…..।

उदाहरण के लिए वस्तुओं की कीमतों, व्यक्तियों की ऊँचाई व भार तथा उनकी आय को अविछिन्न चर कहा जा सकता है तो इसे विछिन्न चर कहेंगे जैसे पूर्ण संख्या (whole number) को विछिन्न चर कहते हैं। जैसे-एक श्रेणी में विद्यार्थियों की संख्या आदि।

प्रश्न 16. एक आदर्श वर्गीकरण के आवश्यक तत्त्वों का उल्लेख कीजिए।

(Enumerate the essential elements of a good classification.)

उत्तर-एक आदर्श वर्गीकरण के आवश्यक तत्त्व निम्नलिखित हैं-

(i) वर्गीकरण निरन्तर का आकार उचित होना चाहिए। (ii) वर्गीकरण सरल होना चाहिए।

(iii) उसमें निरन्तरता का गुण होना चाहिए। (iv) वह शुद्ध होना चाहिए। (iv) वह उद्देश्य के अनुकूल होना चाहिए। (vi) वह लोचदार होना चाहिए। (vii) उसमें व्यापकता का गुण होना चाहिए। (viii) उसमें सजातीयता का गुण होना चाहिए।

प्रश्न 17. सांख्यिकी में जनसंख्या (समग्र) का क्या अभिप्राय है ? एकल, द्वि तथा बहु जनसंख्या समझाएँ।

(Explain the term population as used in statistics. Define : (a) univariate,(b) bivariate and (c) multivariate population. Give examples.)

उत्तर-सांख्यिकी में जनसंख्या (समग्र) से अभिप्राय अनुसंधान क्षेत्र की सभी इकाइयों से होता है। उदाहरण के लिए यदि किसी पाठशाला में पढ़ने वाले विद्यार्थियों के मानसिक स्तर का अध्ययन करना चाहते हैं तो पाठशाला के सभी विद्यार्थी सांख्यिकी की दृष्टि से ‘जनसंख्या’ कहलाते हैं। जनसंख्या को समग्र भी कहते हैं। रोसन्दर (Rosander) के अनुसार, “समग्र विचाराधीन

विषय इकाइयों का योग होता है।”

एकल समग्र से अभिप्राय है समग्र से सम्बन्धित केवल एक चर । जैसे जनसंख्या की केवल आय । द्वि-समग्र से अभिप्राय है समग्र से सम्बन्धित दो चर । उदाहरण के लिए एक कक्षा के सभी छात्रों की ऊंचाई तथा वजन ।

बहु जनसंख्या से अभिप्राय समग्र के विषय से सम्बन्धित बहुत सारी जानकारी के आँकड़े। उदाहरण के लिए सभी परिवारों के उपभोग की सभी मदों का व्यय ।

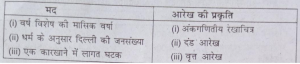
प्रश्न 18. निम्नलिखित को प्रस्तुत करने के लिए किस प्रकार का आरेख प्रभावी होता है?

(क) वर्ष विशेष की मासिक वर्षा,

(ख) धर्म के अनुसार दिल्ली की जनसंख्या का संघटन,

(ग) एक कारखाने में लागत घटक ।

(What kind of diagram are more effective in representing the following ?)

(a) Monthly rainfall in a year

(b) Composition of population of Delhi by region

(c) Composition of cost in a factory

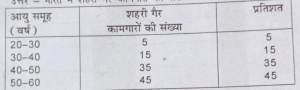
प्रश्न 19. मान लिजिए आप भारत में शहरी गैर-कामगारों की संख्या में वृद्धि तथा भारत में शहरीकरण के निम्न स्तर पर बल देना चाहते हैं, जैसा कि उदाहरण 4.2 में दिखाया गया है, आप उसका सारणीयन कैसे करेंगे?

(Suppose you want to emphasise the increase in the share of urban non-workers and lower level of urbanisation in India as shown in example

4.2. How would you do in the tabular form ?)

उत्तर – भारत में शहरी गैर-कामगारों की संख्या-

                          दीर्घ उत्तरीय प्रश्न

                  (Long Answer Type Questions)

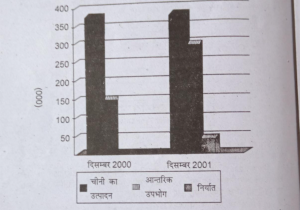
प्रश्न 1. भारतीय चीनी उद्योग संघ ने बताया कि दिसम्बर 2001 से पहले 15 दिन चीनी का उत्पादन लगभग 3,87,000 टन था जबकि पिछले वर्ष 2000 में उन्हीं 15 दिनों का उत्पादन 3,78,000 टन था।

दिसम्बर 2001 के पहले 15 दिनों में आन्तरिक उपभोग के लिये 2,83,000 टन चीनी खरीदी गई और निर्यात के लिए 41,000 टन जबकि पिछले वर्ष इन्हीं दिनों में 1,54,000 टन चीनी आन्तरिक उपभोग के लिए ली गई थी।

(i) आँकड़ों को तालिका में प्रस्तुत करें।

(ii) यदि अपने इन आँकड़ों को आरेख में प्रदर्शित करना है तो आप किस प्रकार का आरेख प्रयोग करेंगे और क्यों?

(iii) इन आंकड़ों को आरेख में प्रकट करें।

The Indian Sugar Mills Association reported that a sugar production during the first fort night of December 2001 was about 3,87,000 tonnes as

against 3,78,000 tonners during the same fortnight last year (2000). The sugar from factories during the first fortnight of December 2001 was 2,83,000 tonnes for internal consumption and 41,000 tonnes for exports as against 1,54,000 tonnes for inte nal consumption and not for exports during the same fortnight lase season.

(i) Present the data in tabular form.

(ii) Suppose you were to present these data in diagram which form of the diagram would you use and why?

(iii) Present those diagram diagrammatically.

उत्तर-(i) भारत में चीनी उत्पादन (Production of Sugar in India)-

(ii) यदि हमें इनको आँकड़ों में प्रदर्शित करना है तो बहु दंड आरेख में प्रदर्शित करेंगे, क्योंकि यह आरेख दो या दो से अधिक तथ्यों का तुलनात्मक अध्ययन करने के लिए सबसे अधिक उपयोगी है।

प्रश्न 2. निम्नलिखित तालिका अनुमानित क्षेत्रीय वास्तविक वृद्धि दरों को प्रतिशत में प्रदर्शित करती है । इन आँकड़ों को बहु समय शृंखला ग्राफ में प्रदर्शित करें।

(The Following table shown the estimated sectoral real growth rates (percentage change over the previous year) in GDP at the factor cost. Represent the data as multiple time series graph.)

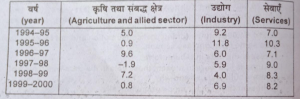
उपर्युक्त आँकड़ों को बहु काल-श्रेणी आरेख द्वारा प्रस्तुत करें।

उत्तर-

प्रश्न 3. निम्नलिखित आँकड़ों का आयत आरेख बनाएँ तथा बहुलक ज्ञात करें।

(Draw histogram with the help of the data given below and determine mode.)

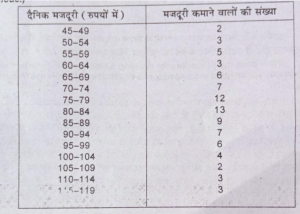
उत्तर – आँकड़ों का आवृत्ति आरेख बनाने से पहले हम संशोधित वर्ग बनाएँगे।

प्रश्न 4. यदि किसी बारम्बारता सारणी में समान वर्ग अन्तरालों की तुलना में वर्ग अंतराल असमान हों, तो आयत चित्र बनाने की प्रक्रिया किस प्रकार भिन्न होगी?

(How does the procedure for drawing a histogram differ when class intervals are unequal in comparison to equal class intervals in a frequency

table?)

उत्तर-आवृत्ति तालिका में वर्गान्तर समान भी हो सकते हैं और असमान भी। दोनों प्रकार के वर्गान्तर से आयत चित्र बनाने के विधि कुछ भिन्न है। जब सभी वर्गान्तर समान हैं तो सभी आयतों की चौड़ाई समान रहती है, परन्तु आयतों की ऊँचाई वर्गों की आवृत्तियों पर निर्भर करती है। जितनी आवृत्तियाँ अधिक होंगी आयतों की ऊँचाई भी उतनी ही अधिक होगी। इसके अतिरिक्त वर्गान्तर समान होने पर आवृत्तियों में कोई फेरबदल नहीं हो जाती, आवृत्तियों को मौलिक रूप में प्रस्तुत किया जाता है। इसके विपरीत जब वर्गान्तर समान नहीं होते तो वर्गान्तरों की ऊँचाई करने के लिए, आवृत्तियों का संशोधन किया जाता है। मान लो न्यूनतम वर्गान्तर 10 है और वर्ग.20-40 का वर्गान्तर 20 है जो न्यूनतम वर्गान्तर का दोगुना है। अत: इस वर्ग को संशोधित आवृति 20 के स्थान पर 10 (20 – 2) होगी। मान लो 40-70 वर्गान्तर की आवृत्तियाँ 15 हैं। यह वर्गान्तर न्यूनतम वर्गान्तर का तीन गुना है। अत: इसकी संशोधित आवृत्ति 5 (15 + 2) होगी ।

प्रश्न 5. नीचे दी गई आवृत्ति वितरण के आधार पर ‘से कम’ संचयी आवृत्ति वक्र बनाएं।

(Draw less than cumulative frequency curve with the help of following frequency distribution.)

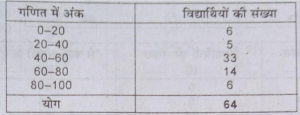
उत्तर-

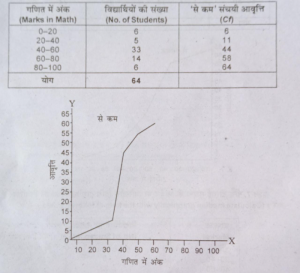
गणित में अंक

प्रश्न 6. नीचे दी गई आवृत्ति वितरण के आधार पेर ‘से अधिक’ संचयी आवृत्ति वक्र बनाएँ। (Draw-more than cumulative frequency curve with the help of following distribution)

गणित में अंक

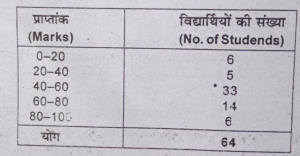
प्रश्न 7. नीचे दी गई सूचना के आधार पर आरेखीय विधि द्वारा माध्यिका का निर्धारण करें। (Calculate median graphically with the help of following data.)

उत्तर-

प्रश्न 8. निम्नलिखित सूचना को एक वृत्त आरेख में दिखाएँ-

(Show the following data in pie-diagram.)

उत्तर-

प्रश्न 9. एक सारणी के मुख्य भागों का वर्णन करें।

(Explain the main parts of a table.)

उत्तर-एक सारणी के मुख्य भाग (Main parts of a Table)-एक सांख्यिकी सारणी के मुख्य भाग इस प्रकार हैं-

(i) सारणी की संख्या (Table Number)-सारणी को सबसे पहले एक संख्या (सारणी संख्या) अर्थात 1.2, 3… आदि दी जानी चाहिए । एक अध्ययन में तालिकाएँ जिस क्रम में बनाई जाती हैं उसी के अनुसार उनकी संख्या दी जानी चाहिए । सारणी संख्या से उन्हें ढूँढ़ने में सहायता मिलती है तथा उनका उल्लेख सरलता से किया जा सकता ।

(ii) शीर्षक (Title)-प्रत्येक सारणी में संख्या के बाद सबसे ऊपर उसका शीर्षक दिया जाना चाहिए । शीर्षक मोटे अक्षरों में लिखा जाना चाहिए ताकि तुरन्त ही ध्यान आकर्षित कर सके। शीर्षक सरल, स्पष्ट और छोटा होना चाहिए। शीर्षक इतना स्पष्ट होना चाहिए कि उसे पढ़ते ही ज्ञात हो जाए कि-(i) आँकड़े किस समस्या (What) से संबंधित हैं। (ii) आँकड़े किस समय (When) से संबंधित हैं। (iii) आँकड़े किस स्थान (Where) से संबंर्बोधत हैं । (iv) आँकड़ों का वर्गीकरण किस प्रकार किया गया है। एक अच्छा शीर्षक छोटा, परन्तु पूर्ण होता है।

(iii) शीर्ष टिप्पणी (Head Note)-यदि शीर्षक से पूरी सूचना प्रकट नहीं होती तो उसके तुरन्त नीचे शीर्ष टिप्पणी (Head Note) दी जाती है। इसमें एक अतिरिक्त सूचना दी जाती है जो शीर्षक में नहीं दी जा सकी। उदाहरण के लिए शीर्षक टिप्पणी में यह बताया जाता है कि आँकड़े किस इकाई में व्यक्त किए गए हैं। उन्हें कोष्ठक (Brackets) में लिखा जाना चाहिए।

(iv) पंक्ति शीर्षक (Stubs)-सारणी की पंक्तियों (Rows) के शीर्षक को पंक्ति शीर्षक कहा जाता है। इसके द्वारा सरल भाषा में ज्ञात होता है कि पंक्तियों द्वारा क्या दिखाया जा रहा है।

(v) उपशीर्षक (Caption)-सारणी के स्तंभों (Columns) के शीर्षक को उपशीर्षक कहा जाता है । इसके शीर्षक से यह ज्ञात होता है कि कॉलम मद की किस विशेषता को बता रहे हैं।

प्रश्न 10. अन्तर बताएँ।

(Distinguish between.)

(i) दंड आरेख तथा (Bar diagram), (ii) आयत चित्र (Histogram)

उत्तर-दंड आरेख तथा आयत चित्र में अन्तर (Difference between bar diagram and histogram)- दंड आरेख वह आरेख है जिसमें आँकड़ों को दंडों के रूप में प्रस्तुत किया जाता है। दंडों की ऊंचाई चरों के मूल्यों पर निर्भर करती है जबकि इनकी चौड़ाई केवल आरेख को आकर्षक बनाने के लिए ली जाती है। दंडों के बीच दूरी समान होती है। ये समानान्यतः व्यक्तिगत मूल्यों, कालश्रेणियों, भौगोलिक श्रेणियों को प्रदर्शित करने में प्रयोग में लाई जाती हैं। इसके विपरीत आयत चित्र आवृत्ति वितरण को प्रस्तुत करता है। इसमें वर्ग अन्तरालों को आवृत्तियों के समीपवर्ती (Adjacent) आयतों में प्रकट किया जाता है । इसमें वर्ग अन्तरालों को x अक्ष पर लेते हैं तथा आवृत्तियों को Y अक्ष पर लेते हैं।

प्रश्न 11. आरेखों द्वारा सांख्यिकीय आँकड़ों के प्रदर्शन लाभों का वर्णन कीजिए।

(Give merits of statistical data presentation by diagram.)

उत्तर – आरेखों के लाभ (Advantages of Diagrams)- यह सर्वविदित है कि जैसे-जैसे समंकों का जमघट अधिक होता जाता है, उन्हें समझने में असुविधा होती है तथा समय लगता है। जनसाधारण अंकों में रुचि नहीं रखते हैं। यदि हम अपनी बातों को अंकों के द्वारा समझाने की बजाय किसी अन्य सरल साधन द्वारा समझाने का प्रयल करें, जहाँ अंकों का कम-से-कम

प्रयोग किया गया हो, तो हमारी बात जनसाधारण के लिए सरल, समझने तथा बाद करने के योग्य हो जाती है। आरेखों के प्रमुख लाभ निम्नलिखित है-

(i) सरल (Simple)-आरेखों की सहायता से जटिल आंकड़ों को सरल तथा सुबोध बनाया जा सकता है।

(ii) समझने में सुगमता (Easy to understand)-आरेखों को समझने के लिए विशेष शिक्षा या ज्ञान की आवश्यकता नहीं होती।

(iii) समय व श्रम की बचत (Saving of time and labour)-आरेखों की सहायता से आँकड़ों समझने में बहुत कम समय लगता है।

(iv) अधिक समय तक स्मरणीय (Memorable for a long time)-अकों को कुछ समय बाद भूल जाना स्वाभाविक है, लेकिन आरेखों द्वारा आंकड़ों की एक ऐसी छाप मस्तिष्क पर पड़ जाती है कि ऑकई बहुत दिनों तक याद रहते हैं।

(v) आरेख आकर्षक होते हैं (Diagrams are attractive)-अंकों को अपेक्षा रेखाचित्र अधिक आकर्षक होते हैं। इसलिए मेलों, प्रदर्शनियों आदि में जनता को प्रभावित करने के आरेखों का प्रयोग अधिक उपयोगी होता है।

(vi) तुलना में सहायक (Easy to comparison)-रेखाचित्रों की सहायता से सांख्यिकी सामग्री में तुलना बहुत सरल हो जाती है। उदाहरणार्थ दिल्ली विश्वविद्यालय के पिछले वर्ष और इस वर्ष के परीक्षा परिणामों की तुलना रेखाचित्रों द्वारा बड़े सुचारु रूप से की जा सकती है।

(vii) सूचना प्रसार में सहायक (Publicity)-रेखाचित्रों द्वारा सूचना प्रसार आसानी से किया जा सकता है।

(viii) सृजनात्मक मनोरंजन (Creative entertainment) -रेखाचित्र सूचना प्रदान करने के साथ-साथ मनोरंजन भी करते हैं। अंकों को देखने से जहाँ आँखें तिलमिला जाती हैं, वहाँ आरेखों को देखने से रुचि बढ़ती है और मनोरंजन भी हो जाता है।

(ix) सार्वभौमिक उपयोगिता (Universal Utility)- विभिन्न लाभों के कारण अनेक क्षेत्रों में सांख्यिकीय रेखाचित्रों का बहुत प्रयोग होता है। व्यापार, वाणिज्य

विज्ञापन के क्षेत्र में ये बहुत उपयोगी और महत्वपूर्ण होते हैं । इस प्रकार रेखाचित्रों की उपयोगिता सार्वभौमिक है। ये सभी क्षेत्रों में नवजीवन प्रदान करते हैं।

प्रश्न 12. सारणीयन के लाभ लिखें।

(Write down the advantages of tabulation)

उत्तर – सारणीयन के लाभ (Advantages of tabulation)

(i) समझने में सरलता (Easy to understand)-सारणी से आँकड़ों को सरलता से समझा जा सकता है, क्योंकि सारणी आंकड़ों को व्यवस्थित रूप में प्रस्तुत करती है।

(ii) संक्षिप्त (Simple)-सारणी द्वारा अव्यवस्थित आँकड़ें कम-से-कम स्थान में इस प्रकार संक्षिप्त रूप में प्रस्तुत किए जाते हैं कि उनसे अधिक-से-अधिक सूचना प्राप्त हो सके।

(iii) तुलना में सुविधा (Convenient in comparision)- सारणी द्वारा आंकड़ों को विभिन्न वर्गों में प्रस्तुत किया जाता है। अतः उनकी तुलना करना सुविधाजनक हो जाता है।

(iv) प्रस्तुतीकरण में सहायक (Helpful in Presentation)-सारणी की सहायता से ही आँकड़ों को आरेखों तथा रेखा-आरेखों द्वारा आकर्षक ढंग से प्रस्तुत करना संभव हो जाता है।

(v) विश्लेषण में सहायक (Helpful in Analysis)-सारणी द्वारा आंकड़ों के विश्लेषण में सहायता मिलती है। आंकड़ों को सारणी के रूप में व्यवस्थित करके ही माध्य (Mean), उपकिरण (Dispersion) आदि ज्ञात किए जाते हैं।

(vi) आंकड़ों की मुख्य विशेषताएँ स्पष्ट हो जाती हैं (Clarifies the Chief Characteristic of Data) -सारणी द्वारा आँकड़ों की मुख्य विशेषताएँ स्पष्ट हो जाती हैं। आँकड़ों को याद रखना भी सरल हो जाता है।

(vii) बचत (Economic)-सारणी द्वारा आँकड़ों को कम स्थान में प्रस्तुत किया जा सकता है। इसके फलस्वरूप समय तथा कागंज की बचत होती है। आवश्यक आँकड़ों को आसानी से ज्ञात किया जा सकता है।

प्रश्न 13. आँकड़ों के प्रस्तुतीकरण में विवरणात्मक तथा सारणीयन विधियों की तुलना करें।

(Compare the descriptive and tabular methods of presenting data.)

उत्तर – आंकड़ों का प्रस्तुतीकरण कई विधियों से किया जा सकता है। उनमें दो विधियाँ विवरणात्मक विधि तथा सारणीयन विधि है। विवरणात्मक विधि से आँकड़ों का विवरण दिया जाता है जैसा कि आर्थिक सर्वेक्षण 2002 के अनुसार भारत में 2000-2001 में खाद्यान्नों का

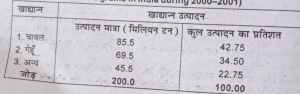
उत्पादन 2000 मिलियन टन था। जिसमें चावल, गेहूँ और अन्य फसलों का उत्पादन क्रमश:85.5.690 और 45.5 मिलियन टन था। कुल उत्पादन में इनका प्रतिशत योगदान क्रमशः मिलियन टन था। कुल उत्पादन में इनका प्रतिशत योगदान क्रमश: 42.75%, 34.50% और 22.75% था।

सारणीयन विधि में ऊपर दिए आँकड़ों को एक सारणी में प्रस्तुत किया जाता है ताकि आँकड़ों को सरलता से समझे जा सके । ऊपर दिए गए तथ्यों को सारणी में निम्न प्रकार प्रस्तुत कर सकते हैं-

2000-2001 में भारत में खाद्यान्नों का उत्पादन

(Production of food grains in India during 2000-2001)

प्रश्न 14. निम्नलिखित को संक्षेप में समझाइए (Write short notes on)-

(अ) विवर्तमुखी वर्ग (Open end Classes), (ब) असमान वर्गान्तर (Unequal Class Interval), (स) संचयी आवृत्ति वितरण (Cumulative Frequency Distribution) |

उत्तर-(अ) विवर्तमुखी वर्ग-विर्वतमुखी वर्ग वह है जिसमें या तो निम्नतम वर्ग की निम्न सीमा या उच्चतम वर्ग की ऊपरी सीमा को छोड़ा है। इस प्रकार के वर्गों का प्रयोग बहुत कम होता है, क्योंकि विवर्तमुखी वर्ग का मध्य मूल्य नहीं ज्ञात कर सकते । उदाहरणार्थ-10 से कम,

10-20, 20-30, 30-40, 40 और अधिक ।

(ब) असमान वर्गान्तर-असमान वर्गान्तर से अभिप्राय ऐसी अखंडित श्रृंखला से है जिसमें वर्गों के बीच का अन्तर एक समान नहीं होता। हम ऐसे वर्गों की आवृत्ति की तुलना नहीं कर सकते । आवृत्तियों की तुलना करने के लिए हम वर्गान्तरों को समान मानकर आवृत्तियों की

पुनर्गणना द्वारा प्रत्येक वर्ग की आवृत्तियाँ ज्ञात करके तुलना करते हैं।

(स) संचयी आवृत्ति वितरण-जब विभिन्न मूल्यों की आवृत्तियों को क्रमशः जोड़कर रखा जाता है तो उसे संचयी आवृत्ति वितरण कहते हैं। स्पष्ट है कि अन्तिम वर्ग की संचयी आवृत्ति सब वर्गों की आवृत्तियों का योगफल होता है। संचयी आवृत्ति वितरण को दो रूपों में व्यक्त किया जाता है-(i) ‘से कम’ (Less than type) (ii) ‘से अधिक’ (More than type) |

प्रश्न 15. संचयी आवृत्ति वितरण किसे कहते हैं ? इसका क्या महत्त्व है ?

(What do you mean by cumulative frequency distribution ? What is its importance ?)

उत्तर-संचयी आवृत्ति वितरण (Cumulative frequency distribution)-संचयी आवृत्ति वितरण उस आवृत्ति वितरण को कहते हैं, जिसमें आवृत्तियों को सरल विधि से वर्गानुसार अलग-अलग न लिखकर संचयी रूप में लिखा जाता है। इस प्रकार के आवृत्ति वितरण के

अन्तर्गत केवल एक सीमा (निचली, ऊपरी) दी जाती है। यदि वर्ग समूह में निचली सीमा के आधार पर संचयी आवृत्ति दी गई है तो ‘से कम’ शब्दों का प्रयोग लिख कर किया जाता है। दोनों पर की गई संचयो आवृत्तियों के उदाहरण नीचे दिए गए हैं।

‘से कम’ संचयी आवृत्ति श्रेणी-

‘से अधिक’ संचयी आवृत्ति श्रेणी

संचयी आवृत्ति वितरण का महत्त्व (Importance of cumulative frequency distribution)-संचयी आवृत्ति वितरण का महत्त्व निम्नलिखित बातों से स्पष्ट हो जाता है-

(i) संचयी आवृत्ति वितरण की सहायता से हम किसी दिए गए चर से कम या अधिक मूल्य ज्ञात कर सकते हैं।

(ii) विभाजन मूल्यों को ज्ञात करने के लिए इसका प्रयोग किया जा सकता है।

(iii) किसी वर्गान्तर विशेष में सम्मिलित मदों की संख्या भी ज्ञात की जा सकती है।

प्रश्न 16, आयत बहुभुज बनाने के लिए असमान वर्गान्तर पर आवृत्तियों का संशोधन क्यों किया जाता है ? आवृत्तियों को संशोधित करने की विधि लिखो।

(Why are frequency of unequal class intervals modified for drawing polygon ? Write down the methods of modifying the frequency)

उत्तर-बई वानर को न्यूनतम वर्गान्तर के बराबर लाने के लिए आवृत्तियों में संशोधन किया जाता है। मान लो न्यूनतम वर्गान्तर 10 है और उच्च वर्ग (40-70) म वान्तर 30 है और उसकी आवृत्ति 15 है। अत: 40-70 वर्ग के तीन वर्ग 40-50,50-60 तथा 60-70 बनते हैं और उनको आवृत्तियाँ 15 तीन वर्षों में बँट जाती हैं और प्रत्येक वर्ग की आवृत्ति 5(5+5+5) होती है।

आवृनियों में संशोधन करने के लिए न्यूनतम वर्गान्तर लेते हैं। कोई वर्गान्तर न्यूनतम वर्गान्तर से जितना गुणा होता है उसी अनुपात में उसकी आवृत्ति कम कर दी जाती है । संशोधित आवृत्ति निकालने के लिए निम्न सूत्र प्रयोग किया जाता है-

संशोधित आवृत्ति =न्यूनतम वर्गान्तर /दिया गया वर्गान्तर× दिए गए वर्ग की आवृत्ति

प्रश्न 17. निम्नलिखित आँकड़ों को एक आयत चित्र द्वारा प्रस्तुत कीजिए-

(Present following data in the form of a histogram.)

उत्तर-

प्रश्न 18. निम्नलिखित आंकड़ों से एक आयत चित्र बनाइए।

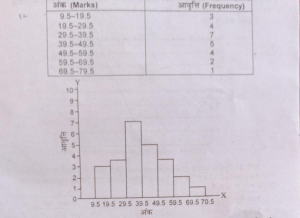
(Prepare a Histogram from the following data.)

उत्तर – प्रश्न में वर्गान्तर समावेशी विधि (Inclusive method) द्वारा दिए गए हैं। अतः इनमें पहले संशोधन करना आवश्यक होगा ताकि समीपवर्ती आयतें बन जाएँ।

संशोधित वर्गान्तर (Adjested Class Intervals)

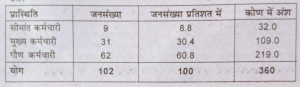
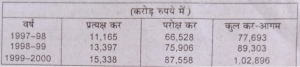
प्रश्न 24. भारत सरकार को पिछली तीन वर्षों के दौरान करों से प्राप्त आगम के बारे में निम्न जानकारी उपलब्ध है-

वर्ष 1997-98 में सरकार को कर-आगम के रूप में कुल 77,693 करोड़ रुपए की प्राप्ति हुई। इसमें से 11,165 करोड़ रुपए प्रत्यक्ष करों तथा 66,528 करोड़ रुपए परोक्ष करों के रूप में प्राप्त हुए । वर्ष 1998-99 में यह राशि क्रमश: 89,303 करोड़ रुपए, 13,397 करोड़ रुपए तथा 75,906 करोड़ रुपए थी। 1999-2000 में कुल राशि । 1.02,896 करोड़ रुपए तथा प्रत्यक्ष तथा परोक्ष करों का योगदान क्रमश: 15,338 करोड़ रुपए तथा 87,558 करोड़ रुपए था।

उत्तर – भारत सरकार को करों से प्राप्त आगम

प्रश्न 20. भारत में चीनी निर्यात से आय के आंकड़े नीचे दिए गए हैं। इन्हें निरपेक्ष कालिक आरेख में प्रस्तुत कीजिए-

उत्तर-X अक्ष पर वर्ष और Y अक्ष पर आय (करोड़ रुपए में) प्रस्तुत करते हुए प्रत्येक वर्ष के सामने आय के चिह्नों को लगाइए, फिर चिह्नों को छूती हुई रेखा बनाइए। इस आरेख को निरपेक्ष कालिक आरेख कहते हैं, जैसा कि नीचे आरेख में दिखलाया गया है।

निरपेक्ष कालिक चित्र

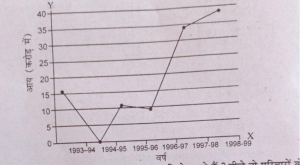
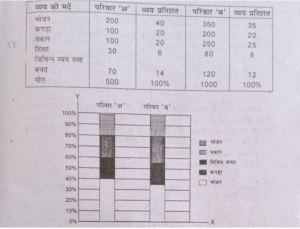
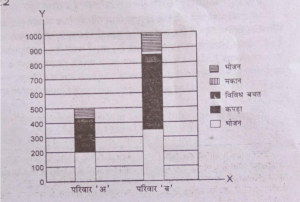
प्रश्न 21. द्विवीम आरेख (Two dimentional) किसे कहते हैं ? नीचे दो परिवारों के आय-व्यय सम्बन्धी आँकड़ें दिए गए हैं। उन्हें द्विविम आरेख द्वारा निरपेक्ष (Absolute) तथा सापेक्ष रूप में दिखाएँ।

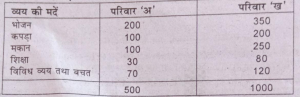
उत्तर-द्वितीय आरेख उस रेखाचित्र को कहते हैं जिसमें लम्बाई के साथ-साथ चौड़ाई को भी दिखाया जाता है। चौड़ाई कुल मूल्यों के अनुपात में होती है। इन्हें निरपेक्ष (Absolute) तथा सापेक्ष (Relative) दो रूपों में दिखाया जा सकता है। निरपेक्ष में दिए गए मूल्यों को आरेख में प्रदर्शित करते हैं जबकि सापेक्ष द्विविमं आरेख के मूल्यों को प्रतिशत में बदलकर प्रतिशत खड़ों में काटकर लिखते हैं।

सापेक्ष द्विविम आरेख (Relative Two Dimensional)- तुलनात्मक अध्ययन के लिए मूल्यों को प्रतिशत में बदल लेते हैं। इस प्रकार ऊंचाई समान हो जाती है और चौड़ाई कुल व्यय के अनुपात में रखी जाती है।

निरपेक्ष द्विविम आरेख (Absolute Two Dimensional)-आय का अनुपात 500:1000=1:2

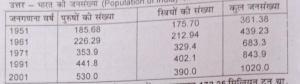
प्रश्न 22. भारत में 1951, 1961, 1971, 1981 और 1991 तथा 2001 की जनगणना में कुल जनसंख्या क्रमश: 361,38, 439,23, 548,16, 683.3, 843.9 तथा 1020 मिलयिन थी। कुल जनसंख्या में पुरुषों की संख्या क्रमश: 185.68, 226.29, 284.05, 353.9, 441.8

तथा 530 मिलियन थी तथा स्त्रियों की संख्या क्रमश: 175.70,212.94,264.11, 329,4,402.1 तथा 490 मिलियन थी। इन आंकड़ों को उपयुक्त सारणी में प्रस्तुत करें।

उत्तर – भारत की जनसंख्या (Population of India) दस लाख में।

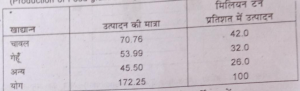
प्रश्न 23. भारत में 2004-2005 में खाद्यान्नों का उत्पादन 172.25 मिलियन टन था, जिसमें चावल, गेहूँ और अन्य फसलों का उत्पादन क्रमश: 70,76, 53.99 और 45.0 मिलियन टन था। कुल उत्पादन में इनका प्रतिशत योगदान क्रमश: 42,0, 32.0 तथा 26.0 था। दी गई सूचना को एक उपयुक्त सारणी में प्रस्तुत कीजिए।

उत्तर-2004-2005 में खाद्यान्नों का उत्पादन

(Production of Food-grain during 2004-2005)

प्रश्न 24. निम्नलिखित विवरण को एक तालिका में प्रदर्शित करें-

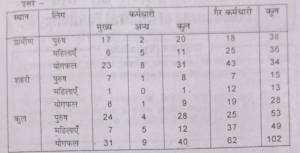
भारत की जनगणना 2001 के अनुसार भारत की जनसंख्या बढ़कर 102 करोड़ हो गई, जिसमें 49 करोड़ महिलाएँ हैं और 53 करोड़ पुरुष हैं । 74 करोड़ लोग ग्रामीण भारत में रहते हैं और केवल 28 करोड़ लोग शहरों में रहते हैं । सम्पूर्ण भारत में 62 करोड़ लोग काम करने वाले व्यक्ति नहीं हैं और 47 करोड़ लोग काम करने वाले हैं। शहरी जनसंख्या में 19 करोड़ काम करने वाले कर्मचारी नहीं हैं और 9 करोड़ काम करने वाले कर्मचारी हैं, जबकि ग्रामीण क्षेत्र में 74 करोड़ लोगों में 31 करोड़ काम पर लगे हुए हैं । इस सूचना को एक तालिका द्वारा दिखाएँ।

(Census of India 2001 reported that India population and risen to 102 crore of which only 49 crore were females against 53 crore males, 74 crore people reside in rural India only 28 crore lived in town or cities. While there 62 crore non-worker population against 47 crore worker in the entire country Urban population had in enen higher share of non-workers 19 crores against the workers 9 crore as compared to the rural pupulation where there were 31 crore workers out of 74 crore population.)

Show above text intabular form.

उत्तर-

                    वस्तुनिष्ठ प्रश्न

           (Objective Type Questions)

प्रश्न 1. निम्नलिखित 1 से 10 तक के प्रश्नों के सही उत्तर चुनें-

(i) दंड-आरेख-

(क) एक विमीय आरेख है।

(ख) द्विवमीय आरेख है।

(ग) विम रहित आरेख है।

(घ) इनमें से कोई नहीं।

(ii) आयत चित्र के माध्यम से प्रस्तुत किए गए आंकड़ों द्वारा हम आलेखी रूप में निम्नलिखित जानकारी प्राप्त कर सकते हैं-

(क) माध्य

(ख) बहुलक

(ग) मध्यिका

(घ) इनमें से कोई नहीं।

(iii) तोरणों के द्वारा आलेखी रूप में निम्न की स्थिति जानी जा सकती है-

(क) बहुलक

(ख) माध्य

(ग) माध्यिका

(घ) उपर्युक्त कोई भी नहीं।

(iv) अंकगणितीय रेखाचित्र के द्वारा प्रस्तुत आंकड़ों से निम्न को समझने में मदद मिलती है-

(क) दीर्घकालिक प्रवृत्ति

(ख) आँकड़ों में चक्रीयता

(ग) आँकड़ों में कालिकता

(घ) उपर्युक्त सभी।

(v) दंड-आरेख के दंडों की चौड़ाई का एक समान होना जरूरी नहीं है । (सही/गलत)

(vi) आयत चित्र में आयतों की चौड़ाई अवश्य एक समान होनी चाहिए । (सही/गलत)

(vii) आयत चित्र की रचना केवल आँकड़ों के सतत वर्गीकरण के लिए की जा सकती है।(सही/गलत)

(viii) आयत चित्र एवं स्तंभ आरेख आँकड़ों को प्रस्तुत करने के लिए एक जैसी विधियाँ है।(सही/गलत)

(ix) आयत चित्र की मदद से बारंबारता वितरण के बहुलक को आलेखी रूप में चलाया जा सकता है ‌।

(सही गलत)

(x) तोरणों में बारम्बारता वितरण को माध्यिका को नहीं बाला जा सकता है (सही गलत)