bihar board class 11 economics | सहसम्बन्ध
bihar board class 11 economics | सहसम्बन्ध
( Correlation)
पाठ्यक्रम (Syllabus)
सहसम्बन्ध शब्द का अर्थ, विभिन्न चरों के बीच में सम्बन्य, सहसम्बन्ध के विभिन मापों की गणना, सम्बन्धों की कोटि तथा दिशा का विवेचन ।
इस अध्याय में आप जानेंगे-:• सहसम्बन्ध शब्द का अर्थ । • दो विभिन चरों के सम्बन्धों की प्रकृति । • चरों के विभिन्न मापों की गणना । • सम्बन्धों की कोटि तथा दिशा का विश्लेषण ।
” याद रखने योग्य बातें (Points to Remember):-
1. सहसम्बन्ध (Correlation) – दो चरों का एक दूसरे से सहानुभूतिपूर्ण एक दिशा में या विपरीत दिशा में बढ़ने या घटने से है।
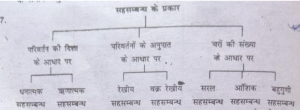
2. सहसम्बन्ध के प्रकार (Types of Correlation)- (i) धनात्मक सह-सम्बन्ध, तथा (ii) ऋणात्मक सहसम्बन्ध।
3. धनात्मक सहसम्बन्ध (Positive Correlation)- दो चरों का एक ही दिशा में बढ़ना या घटना।
4. ऋणात्मक सहसम्बन्ध (Negative Correlation) – दो चरों का एक दूसरे के विपरीत दिशा में चलना।
5. रेखीय सहसम्बन्ध (Linear Correlation)-जो दो श्रेणियों के मूल्यों में परिवर्तन का स्थायी अनुपात होता है, तो इस प्रकार का सहसम्बन्ध रेखीय (Linear) सहसम्बन्ध कहलाता
6. आरेखीय सहसम्बन्ध (Non-LinearCorrelation)- जब एक घर में परिवर्तन अन्य चर के समान अनुपात में नहीं होता तो इसे अरेखीय सहसम्बन्ध कहा जाता है।
8. सहसम्बन्ध की सीमित मात्रा (Limited Quantity of Corelation)-0 से अधिक तथा से कम अर्थात् सहसम्बन्ध की मात्रा (Degree) हमेशा (-1) और (+2) के बीच होती है।
9. सहसम्बन्ध की श्रेणियाँ (Degree of Correlation)-

10. सहसम्बन्ध मापने की विधियाँ (Method of Measuring Correlation)-

11. विक्षेप या प्रकीर्ण चित्र (Scatter Diagram) – यह एक प्रकार का बिन्दु चार्ट होता है।
12. विक्षेप चित्र के प्रकार (Types of Scatter Diagram)-
विक्षेप चित्र के लाभ (Types of Scatter Diagram)- (i) विक्षेप चित्र खींचना सरल है। (ii) x तथा y में रेखीय सम्बन्ध होने की अवस्था में हमें पता चलता है कि x चर में परिवर्तन होने से चर में किस प्रकार परिवर्तन होंगे।
विक्षेप चित्र के दोष (Demerits of Scatter Diagram)- (i) विक्षेप चित्र की सहायता से दो चरों में सम्बन्धों की मात्रा को संख्यात्मक रूप से निश्चित नहीं किया जा सकता।
(ii) विक्षेप चित्रों से हमें कारणों की दिशा का ज्ञान नहीं होता । हमें इस बात का ज्ञान नहीं होता कि x के कारण y में परिवर्तन हुए हैं या y के कारण x में परिवर्तन हुए हैं । (ii) यदि दो से अधिक चर हैं तो उन्हें ग्राफ पेपर पर नहीं दिखाया जा सकता है।
13. कार्ल पियर्सन का सहसम्बन्ध गुणांक (Karl-Pearson’s co-efficient of correlation) – यदि दो चरों x तथा y में रेखीय सम्बन्ध है, तो हम दोनों सहसम्बन्धों को कार्ल पियर्सन के सह-सम्बन्ध गुणांक के द्वारा जान सकते हैं।
14. स्पीयरमैन का कोटि सह-सम्बन्ध (Spearman’s Rank Correlation)-कई बार चरों को संख्या के रूप में नहीं मापा जा सकता। इन चरों को गुण कहा जाता है । अत: उनका सहसम्बन्ध गुणांक स्पीयर में कोटि सहसम्बन्ध से ज्ञात किया जाता है। इस विधि के अंतर्गत
चरों का कोटि क्रम दिया जाता । इसके बाद दो श्रेणियों के क्रमों का अन्तर निकाला जाता है और निम्न सूत्र का प्रयोग किया जाता है :
Rk=1-(£D²)/N(N²-1)
पाठ्यपुस्तक एवं परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्नोत्तर
(Textbook and Other Important Questions for Examination)
अति लघु उत्तरीय प्रश्न
(Very Short Answer Type Questions
प्रश्न 1. सहसम्बन्ध से क्या अभिप्राय है?
उत्तर-दो या अधिक चरों में सम्बन्ध की मात्रा के मापन को सहसम्बन्ध कहते हैं।
प्रश्न 2. सहसम्बन्ध गुणांक सदैव – (ii) तथा +1 के बीच होता है । गणित की भाषा में इसे आप किस प्रकार व्यक्त करेंगे?
उत्तर-1≤r≤+1
प्रश्न 3. धनात्मक (Positive) सहसम्बन्ध से क्या अभिप्राय है?
उत्तर-जब दो चर x तथा y एक ही दिशा में विचरित (परिवर्तित) होते हैं, तो उनके बीच सम्बन्ध धनात्मक सह-सम्बन्ध कहलाता है।
प्रश्न 4. विलोम (Negative) सहसम्बन्ध से क्या अभिप्राय है?
उत्तर-जब एक चर में परिवर्तन दूसरे चर के विपरीत होता है तो उनके बीच सम्बन्ध विलोम सहसम्बन्ध कहलाता है।
प्रश्न 5. धनात्मक सहसम्बन्ध का एक उदाहरण दीजिए।
उत्तर-किसी वस्तु की कीमत तथा पूर्ति के बीच धनात्मक सहसम्बन्ध पाया जाता है।
प्रश्न 6. विलोम सहसम्बन्ध का एक उदाहरण दीजिए।
उत्तर-किसी वस्तु की मांगी गई मात्रा तथा उसके मूल्य के बीच विलोम सहसम्बन्ध पाया जाता है।
प्रश्न 7. यदि x तथा y स्वतंत्र चर हों, उनके बीच सहसम्बन्ध गुणांक (r)(Coefficient of Correlation) का क्या मूल्य होगा?
उत्तर-सहसम्बन्ध गुणांक (r) = 0
प्रश्न 8. यदि दो श्रेणियों में पूर्ण सहसम्बन्ध (Perfect Correlation) है तो ऐसी स्थिति में सहसम्बन्ध गुणांक (r) का मूल्य क्या होगा?
उत्तर-सहसम्बन्ध गुणांक (r) = + 1
प्रश्न 9. सहसम्बन्ध ज्ञात करने की तीन प्रमुख विधियों के नाम लिखिए।
उत्तर-(i) विक्षेप चित्र (ii) काल पियर्सन का सहसम्बन्ध गुणांक तथा (iii) कोटि अन्तर विधि। ।
प्रश्न 10. विक्षेप चित्र का प्रमुख दोष क्या है ?
उत्तर-विक्षेप चित्र सहसम्बन्ध की मात्रा का संख्यात्मक माप नहीं देता।
प्रश्न 11. सहसम्बन्ध गुणांक क्या है ?
उत्तर-सहसम्बन्ध गुणांक दो चरों के बीच सहसम्बन्ध की मात्रा का संख्यात्मक माप (Numerical Measurement) है।
प्रश्न 12. यदि r= + 1, तो इसका क्या अर्थ है ?
उत्तर-यदि r = + 1 तो इसका अर्थ पूर्ण धनात्मक यसा ऋणात्मक सहसम्बन्ध है।
प्रश्न 13. सहसम्बन्ध गुणांक (r)की सीमाएँ लिखिए।
उत्तर-सहसम्बन्ध गुणांक (r) प्रायः – 1 तथा +1 के बीच होता है। गणित की भाषा में –
प्रश्न 14. यदि r=0 तो इसका क्या अर्थ है ?
उत्तर-यदि r= 0 तो इसका अर्थ सहसम्बन्ध का अभाव है।
प्रश्न 15. सहसम्बन्ध गुणांक को ज्ञात करने का कार्ल पियरसन द्वारा दिया गया सूत्र
लिखिए।
उत्तर-r= £(x-X)(Y-Y)/√£(X-X)²[√£(Y-Y)²]
प्रश्न 16. कोटि सहसम्बन्ध गुणांक का प्रतिपादन किसने किया ?
उत्तर-स्पियरमैन ने।
प्रश्न 17. कोटि सहसम्बन्ध विधि का प्रयोग कहाँ उपयुक्त होता है ?
उत्तर-कोटि सहसम्बन्ध विधि का प्रयोग वहाँ उपयुक्त होता है जहाँ तथ्यों का प्रत्यक्ष संख्यात्मक माप संभव न हो तथा उन्हें क्रम के अनुसार रखा जा सकता हो ।
प्रश्न 18. सहसम्बन्ध को मापने के लिये स्पियरमैन का सूत्र लिखो।
उत्तर-r=6£D²/ N(N²-1)
प्रश्न 19. सहसम्बन्ध को रेखीय कब कहा जाता है?
उत्तर-जब दो श्रेणियों के मूल्यों में परिवर्तन का अनुपात स्थायी होता है तो उसे रेखीय सहसम्बन्ध कहते हैं।
प्रश्न 20. सहसम्बन्ध की अनुपस्थिति से क्या अभिप्राय है ?
उत्तर-जब दो श्रेणियों के मूल्यों में किसी प्रकार का सम्बन्ध नहीं होता तो ऐसी स्थिति में सहसम्बन्ध की अनुपस्थिति होती है अर्थात् सहसम्बन्ध का अभाव होता है । सहसम्बन्ध गुणांक का मूल्य शून्य होता है।
प्रश्न 21. यदि विक्षेप रेखा का झुकाव ऊपर से नीचे दाहिनी ओर हो तो वर्गों में किस प्रकार सहसम्बन्ध होगा?
उत्तर-दो चरों में ऋणात्मक सम्बन्ध होगा।
प्रश्न 22. निम्नलिखित आंकड़ों में सहसम्बन्ध गुणांक ज्ञात कीजिए।
X 1 2. 3 4 5 6
Y 46 43 40 37 34 31
उत्तर-%r =-1 क्योंकि चरों का विपरीत सम्बन्ध है
प्रश्न 23. जब कोटियाँ (Ranks) समान होती हैं तो ऐसी अवस्था में Rk की गणना करने के लिये कौन सा सूत्र लगाया जाता है ? वह सूत्र लिखें।
उत्तर-कोटियाँ समान होने का अवस्थ में Rk की गणना के लिये निम्नलिखित सूत्र का प्रयोग किया जाता है-
rk=1-6[D²+(m²-m1)/12 ( m³2-m2)/12+…..]\n(n²-1)
24.r को सह के माप का सहचर क्यों कहा जाता है?
उत्तर-क्योंकि r सहवर को मापता है न कि कारणों को।
प्रश्न 25. क्या आंकड़ों के प्रकार के आधार पर ,-1 तथा +1 के बाहर स्थित हो सकता है?
उत्तर-नहीं।
प्रश्न 26. सरल सहसम्बन्ध गुणांक की तुलना में कोटि सहसम्बन्ध गुणांक कय अधिक परिशुद्ध होता है?
उत्तर-कोटि सहसम्बन्ध साधारण सहसम्बन्ध गुणांक से इस अवस्था में अच्छा है जब चरों का मापन सही ढंग से किया जा सके।
प्रश्न 27. क्या सहसम्बन्ध के द्वारा कार्यकारण संबंध की जानकारी मिलती है ?
उत्तर-नहीं।
प्रश्न 28. क्या शून्य सहसम्बन्ध का अर्थ स्वतंत्रता है?
उत्तर-हाँ।
प्रश्न 29. क्या सरल सहसम्बन्ध गुणांक किसी भी प्रकार के सम्बन्ध को माप सकता है?
उत्तर-नहीं।
प्रश्न 30. साहचर्य के माप के लिए । को सहप्रसरण से अधिक प्राथमिकता क्यों दी जाती है?
उत्तर-साहचर्य के माप के लिए। को तब अधिक प्राथमिकता दी जाती है जब चरम मान दिए गए हों। सामान्यतःrk का मान r से कम या इसके बराबर होता है।
प्रश्न 31. क्या शून्य सहसम्बन्ध का अर्थ स्वतंत्रता है?
उत्तर-नहीं। किन्तु स्वतंत्रता की संभावना बनी रहती है।
प्रश्न 32. कुछ ऐसे घरों की सूची बनाएँ जिनका परिशुद्ध मापन कठिन हो।
उत्तर-निष्पक्षता, धर्मनिरपेक्षता, ईमानदारी, सत्यता, देशभक्ति, सद्भावना, परोपकार, नि:वार्थता
आदि कुछ ऐसे चर हैं जिनका परिशुद्ध मापन कठिन है।
लघु उत्तरात्मक प्रश्न
(Short Answer Type Questions
प्रश्न 1. सहसम्बन्ध की परिभाषा दीजिए । सहसम्बन्ध के निम्न मानों से आपका क्या अभिप्राय है?
Give the definition of Correlation. Give Meanings of the following value:
r=0, r= + 1, f=-1
उत्तर-दो या दो से अधिक चरों में सम्बन्ध की मात्रा मापने को सहसम्बन्ध कहते हैं। सहसम्बन्ध द्वारा विभिन्न चरों में पाये जाने वाले परस्पर सम्बन्धों व मात्रा को दिशा का ज्ञान होता है।
(i) जब r=0, तो इसका अभिप्राय है वि चरों में सहसम्बन्ध का अभाव पाया जाता है।
(ii) जब r=1, तो इसका अभिप्राय है कि दो चरों में पूर्ण धनात्मक सहसम्बन्ध पाया जाता है।
(iii) जब r=1, तो इसका अभिप्राय है कि दो चरों में पूर्ण ऋणात्मक सहसम्यग पाया जाता है।
प्रश्न 2. निम्न अवस्था में सहसम्बन्ध का मूल्य बताओ
(क) सहसम्बन्ध ऋणात्मक तथा पूर्ण ।
(ख)सहसम्बन्ध धनात्मक तथा पूर्ण ।
(ग) कोई सहसम्बन्ध नहीं।
Give the value of Correlation under following position:
(a) Perfect Correlation and Negative.
(b) Perfect Correlation and Positive.
(c) No Correlation.
उत्तर-(a) जब सहसम्बन्ध पूर्ण ऋणात्मक तथा पूर्ण होता है, तो सहसम्बन्ध गुणांक r = -1
(b) जब सहसम्बन्ध गुणांक धनात्मक तथा पूर्ण होता है, तो सहसम्बन्ध गुणांक r= +1
(c) जब कोई सहसम्बन्ध नहीं पाया जाता है तो सहसम्बन्ध गुणांक r=0
प्रश्न 3. धनात्मक तथा ऋणात्मक सहसम्बन्ध की परिभाषा दीजिए तथा प्रत्येक का एक-एक उदाहरण दीजिये।
(Define Positive and Negative correlation and give the example.)
उत्तर-धनात्मक सहसम्बन्ध : जब दो चरों x तथा y में परिवर्तन एक ही दिशा की ओर होता है, तो उनमें धनात्मक सहसम्बन्ध होगा। उदाहरण के लिए यदि आय में वृद्धि के साथ उपभोग में भी वृद्धि होती है तो उपभोग और आय में धनात्मक सहसम्बन्ध है।
ऋणात्मक सहसम्बन्ध : जब दो चरों x तथा y में परिवर्तन विभिन्न दिशाओं में होते हैं अर्थात् जब x चर में वृद्धि होने से y चर में कमी होती है तो उनमें ऋणात्मक सहसम्बन्ध होगा।
प्रश्न 4. पूर्ण सहसम्बन्ध से क्या अभिप्राय है ? इसके दो उदाहरण दीजिए।
(What is Perfect Correlation ? Give two examples.)
उत्तर-यदि दो चरों में मूल्यों के परिवर्तन की मात्रा बिल्कुल समान है, तो उनमें पूर्ण धनात्मक या ऋणात्मक सहसम्बन्ध होता है । ऐसी स्थिति में सहसम्बन्ध का गुणांक (r) का मूल्य +1 होगा।
उदाहरण : (a) कीमत 1 2 3 4 5
पूर्ति 10 20 30 40 50
अत: कीमत तथा पूर्ति में पूर्ण धनात्मक सहसम्बन्ध है।
(b) कीमत : 1 2 3 4 5
50 40 30 20. 10
अत: कीमत और मांग में पूर्ण ऋणात्मक सहसम्बन्ध होगा।
प्रश्न 5. सरल बहुगुणी एवं आंशिक सहसम्बन्ध की परिभाषा दीजिए।
(Defins Simple, Multi Correlation, Partly Correlation.)
उत्तर-सरल सहसम्बन्ध दो चरों में सम्बन्ध की मात्रा का मापन करता है। बहुगुणी सहसम्बन्ध दो से अधिक चरों में सम्बन्ध की मात्रा का मापन करता है। आशिक सहसम्बन्ध भी दो से अधिक चरों का अध्ययन करता है, परन्तु अन्य चरों के प्रभाव को स्थिर रखकर केवल दो चरों का पारस्परिक सम्बन्ध निकलता है।
प्रश्न 6. कार्ल पियरसन का सह-सम्बन्ध गुणांक क्या है ? इसकी गणना का सूत्र दीजिए । इसकी सीमाएँ कौन सी हैं ?
(What is Coefficient of Correlation of Karl Pearson ? Give its formula and limited degree of Correlation.)
उत्तर-कार्ल पियरसन का सहसम्बन्ध गुणांक दो चरों में सम्बन्ध की मात्रा का संख्यात्मक माप है। इसकी गणना का सूत्र निम्नलिखित है-
r= £(X-X)(Y-Y)/√£(X-X)²(Y-Y)²
r = सहसम्बन्ध गुणांक।
सीमाएँ (Limited degree of correlation cd-efficient)-सहसम्बन्ध गुणांक का मान सदैव ही-1 तथा +1 के बीच में होगा। गणित की भाषा में इसे निम्न प्रकार से व्यक्त किया जाता है-
-1 ≤ r ≤+ 1
प्रश्न 7. सहसम्बन्ध ज्ञात करने की कोटि क्रम विधि की विवेचना करो।
(Explain the Ranking Correlation.)
उत्तर-कोटि क्रम विधि के अन्तर्गत सर्वप्रथम x तथा y पद मूल्यों को अलग-अलग कोटि प्रदान किये जाते हैं। सबसे अधिक आकार वाले मूल्य को 1, उससे कम आकार वाले को 2 और इसी प्रकार क्रम निश्चित किये जाते हैं । द्वितीय x के क्रमों में से y के तत्सम्बन्धी क्रम घटाए जाते हैं और कोटि अन्तर निकाले जाते हैं। तृतीय कोटि क्रम वर्ग करके उन वर्गों का जोड़ निकाला जाता है। अन्त में निम्न सूत्र प्रयोग किया जाता है-
R=1-6£D²/N(N²-1)
R= कोटि सहसम्बन्ध गुणांक
£D²= क्रम अन्तर में वर्गों का जोड़
N=पद युग्मों की संख्या।
प्रश्न 8. निम्नलिखित आंकड़ों में विक्षेप चित्र (Scatter Diagram) द्वारा सहसम्बन्ध (Correlation) बताइये:
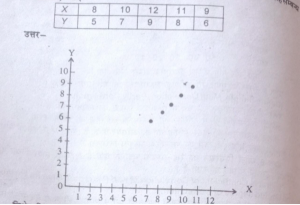
विक्षेप चित्र में स्पष्ट है कि X तथा Y में पूर्ण धनात्मक (Perfect positive) सहसम्बन्ध पाया जाता है।
प्रश्न 9.10 विद्यार्थियों के अंग्रेजी और अर्थशास्त्र के प्राप्तांकों की कोटियों के अन्तर में वर्गों का योग 33 है । कोटि सम्बन्ध गुणांक (Bank Correlation.coefficient) ज्ञात कीजिए।
उत्तर-चिह्नों के रूप में निम्नलिखित दिया हुआ है-
R = 10,£D² = 33
R= 1-6£D²/(N²-1)=1-6×33/10⁰(10-1⁰
=1-198/990=990-198/990=8
प्रश्न 10. पियरसन सहसम्बन्ध गुणांक से कोटि सहसम्बन्ध गुणांक क्यों भिन्न होता है ?
(How does rank correlation differ from correlation co-efficient ?)
उत्तर-पियरसन का सहसम्बन्ध गुणांक दो चरों x एवं Y के बीच रेखीय संबंधों के सही संख्यात्मक मान की कोटि दर्शाता है। जबकि कोटि सहसम्बन्ध जब चरों का सार्थक रूप से मापन नहीं किया जा सकता, जैसे कीमत, आय, वजन आदि । कोटि निर्धारण तब अधिक होता है जब चरों की माप भ्रामक हो।
प्रश्न 11.एक सप्ताह तक अपने स्थानीय बाजार से 5 प्रकार की सब्जियों की कीमतें प्रतिदिन एकत्र करें । उनका सहसम्बन्ध गुणांक परिकलित कीजिए । परिणाम की व्याख्या कीजिए।
(Collect the prices of vegetables from your local market every day for a week. Calculate their correlation co-efficient of these two variable.
Interpret the results.) )
उत्तर-विद्यार्थी स्वयं प्रयत्न करें।
प्रश्न 12. अपनी कक्षा के सहपाठियों के कद मापिए । उनसे उनके बेंच पर बैठे सहपाठी का कद पूछिए । इन दो चरों का सहसम्बन्ध गुणांक परिकलित कीजिए और परिणाम का निर्वचन कीजिए।
(Measure the height of your classmates. Ask them the height of their benchmate calculate the correlation coefficient of these two variables.
Interpret the result.)
उत्तर-विद्यार्थी स्वयं प्रयत्न करें।
प्रश्न 13.rके विभिन्न मानों +1,-1 तथा 0 की व्याख्या करें।
(Interpret the value of r as 1,-1and 0.)
उत्तर-(i) यदि r का मूल्य 1 है तो इसका तात्पर्य यह है कि दो चरों x तथा Y में पूर्णत: धनात्मक सम्बन्ध है।
(ii) यदि r का मूल्य -1 है तो इसका तात्पर्य यह है कि दो चरों X तथा Y में पूर्णत: ऋणात्मक सम्बन्ध है।
(iii) यदि r का मूल्य 0 है तो इसका तात्पर्य यह है कि X तथा Y चरों में कोई सहसम्बन्ध नहीं है।
प्रश्न 14. यदि विक्षेप चित्र में बिन्दु उस सरल रेखा पर जमघट लगाते हैं जो रेखा X अक्ष पर 30° का कोण बनाती है तो आप तथा Yचरों में किस प्रकार का सम्बन्ध पायेंगे?
उत्तर-इससे पता घलता है कि X तथा V में कम मात्रा में सहसम्बन्ध है । दूसरे शब्दों में Y में उसी अनुपात में परिवर्तन नहीं होता जिस अनुपात में X में!
प्रश्न 15. निम्न X और / युग्मों को विक्षेप चित्र में प्रस्तुत कीजिए-

प्रश्न 16. कार्ल पियरसन के सहसम्बन्ध के गुणांक को कैसे परिभाषित किया गया?
(How is Karl Pearson to coefficient of correlation defined ?)
उत्तर-सहसम्बन्ध के ज्ञान को गणितीय विधि से प्रतिपादित करने का श्रेय प्रो. कार्ल पियरसन को है । कार्ल पियरसन का सहसम्बन्ध गुणांक समान्तर माध्य तथा प्रमाप विचलन पर आधारित है। इस गुणांक को गुण परिघात सहसम्बन्ध (Product, moment correlation) कहते हैं। इस सहसंबंध को । कहते हैं। यदि X तथा Y दो चरों का सम्बन्ध रेखिक (Linear) है तो हम उनमें कार्ल पियरसन के सहसम्बन्ध गुणांक की सहायता से सम्बन्ध की मात्रा का ज्ञान प्राप्त कर
सकते हैं।
प्रश्न 17.(क) सहसम्बन्ध गुणांक () की क्या सीमायें हैं ?
(ख) यदि r=+1 या r=-1 है तो दो चरों और Yमें किस प्रकार का सम्बन्ध है ?
(a) What the limits of the correlation co-efficient r?
(b) If r= +1 or r= -1, what kind of relation exists between X and Y?
उत्तर-(क) सह-सम्बन्ध गुणांक हमेशा -1 और +1 की सीमा में होगा।
(ख) यदि r= +1 या r=-1 है तो उसका अभिप्राय है कि दो चरों x तथा Y में सम्बन्ध निश्चित (Exact) है।
यदि r= +1 है तो दोनों चरों में पूर्णतः धनात्मक सम्बन्ध होगा और यदिr=-1 है तो दोनों चरों (x, y) में पूर्णतः ऋणात्मक सम्बन्ध होगा।
दीर्घ उत्तरात्मक प्रश्न
(Long Answer Type Questions)
प्रश्न 1. सहसम्बन्ध गुणांक की विशेषताएँ लिखें।
(Write down the characteristics of correlation coefficient.)
उत्तर-सहसम्बन्ध गुणांक की विशेषताएँ (Properties of correlation coefficient)-
सहसम्बन्ध गुणांक की विशेषताएँ अग्रलिखित हैं-
(i) rकी कोई इकाई (unit) नहीं है। यह एक शुद्ध संख्या है। इसका तात्पर्य यह है कि माप की इकाइयाँ इसका भाग नहीं हैं। दूसरे शब्दों में फुटों में ऊँचाई तथा किलोग्राम में वजन का r 0.7 है।
(ii)r के ऋणात्मक मूल्य का अर्थ है कि दो चरों x तथा Y में विपरीत सम्बन्ध है। एक चर में परिवर्तन होने से दूसरे चर में विपरीत दिशा में परिवर्तन होता है। उदाहरण के लिये जब एक वस्तु की कीमत में वृद्धि होती है तो उसकी मांग में कमी आती है !
(iii) यदि r धनात्मक है तो इसका अभिप्राय है कि x तथा yचर एक ही दिशा की ओर चलते हैं। जब कॉफी (चाय का प्रतिस्थापन) की कीमत में वृद्धि होती है, चाय की मांग में वृद्धि होती है, जब तापक्रम में वृद्धि होती है, आइसक्रीम की बिक्री में वृद्धि होती है।
(iv) यदि r=0 तो x तथा Yचरों में सहसम्बन्ध का अभाव होता है। उनके बीच कोई रैखीय सम्बन्ध नहीं होता।
(v) यदि r = 1 अथवा r=-1 है तो सहसम्बन्ध पूर्णता है। उन दो चरों में सम्बन्ध निश्चित है।
(vi) rका अधिक मूल्य इस बात का संकेत देता है कि दो चरों X तथा Y में दृढ़ रैखीय सम्बन्ध है। इसका मूल्य तभी ऊँचा कहा जायेगा जब यह +1 अथवा -1 के समीप होगा।
(vii) rका कम मूल्य इस बात को इंगित करता है कि दो चरों x तथा Y में कमजोर रेखीय सम्बन्ध है। इसका मूल्य तभी नीचा कहा जायेगा जब वह शून्य के समीप होगा।
(vii) सहसम्बन्ध गुणांक का मूल्य -1 तथा +1 के बीच में होता है। दूसरे शब्दों में
1 ≤ r ≤ 1
यदि किसी प्रश्न में । का मूल्य इस सीमा के बाहर आता है, इसका तात्पर्य यह है कि r की गणना करने में कोई त्रुटि हुई है।
(ix) मूल में परिवर्तन से या पैमाने के परिवर्तन से । के मूल्य पर कोई प्रभाव नहीं रहता।
मान लो. दो चर X तथा Y दिये गये हैं। इन दो चरों को निम्न प्रकार परिभाषित करें-
rxy = ruv
A तथा B क्रमश: X और Y के काल्पनिक औसत (A M.) हैं। B तथा D कॉमन फैक्टर (Common factors) हैं।
प्रश्न 2. विक्षेप चित्र से क्या अभिप्राय है ? इस विधि के द्वारा सहसम्बन्ध कैसे मापा जाता है?
(What do you mean by seatter diagram ? How is correlation measured by this method ?)
उत्तर-विक्षेप चित्र (Scatter Diagram)-विक्षेप चित्र दो चरों के बीच सहसम्बन्ध मापने की एक विधि है। इस विधि के द्वारा सहसम्बन्ध की दिशा के बारे में ज्ञान प्राप्त किया जाता है। विक्षेप चित्र बनाने की प्रक्रिया में निम्नलिखित चरण निहित है-
(i) स्वतंत्र चरों को X अक्ष पर लिया जाता है।
(ii) आश्रित चरों को Y अक्ष पर प्रदर्शित किया जाता है
(iii) बिन्दु अकित समंक से एक मूल्य स्वतंत्र चर कर लिया जाता है तथा एक मूल्य आश्रित चर । इन मूल्यों की सहायता से ग्राफ पेपर पर एक बिन्दु अंकित किया जाता है।
(iv) श्रेणी में जितने जोड़े होते हैं, उतने ही बिन्दु अंकित किये जाते हैं।
(v) बिन्दु जितने एक दूसरे के पास होगे, सहसम्बन्ध को डिग्री उतनी ही अधिक होगी और बिन्दु जितने अधिक बिखरे होंगे, सहसम्बन्धों की डिग्री उतनी ही कम होगी। बिन्दुओं की दिशा को देखकर यह अनुमान लगाया जा सकता है।
विक्षेप चित्र में प्रदर्शित बिन्दुओं की प्रवृत्ति यदि एक निश्चित दिशा में जाने की हो तो दोनों चरों में सहसम्बन्ध होगा। यदि बिन्दु सारे चित्र में फैले हुए हैं तो सहसम्बन्ध की अनुपस्थिति होगी।
यदि बिन्दुओं को छूती हुई सरल रेखा का झुकाव नीचे से ऊपर दहिनी ओर हो तो चरों में धनात्मक सम्बन्ध होगा। यदि बिन्दु सारे चित्र में फैले हुए हैं तो सहसम्बन्ध की अनुपस्थिति होगी।
यदि बिन्दुओं की छूती हुई सरल रेखा का झुकाव नीचे से ऊपर दाहिनी ओर हो तो चरों में धनात्मक सम्बन्ध होगा। इसके विपरीत यदि रेखा का झुकाव ऊपर से नीचे दाहिनी ओर है तो चरों में ऋणात्मक सम्बन्ध होगा।
प्रश्न 3. विक्षेप चित्र के गुण तथा दोष लिखिए।
(Write down the merits and demerits of scatter diagram.)
उत्तर-गुण (Merits)-(i) दो चरों में सम्बन्ध जानने की यह बहुत ही सरल विधि है।
(ii) चित्र पर नजर डालते ही पता चल जाता है कि दो चरों के बीच कोई सम्बन्ध है या नहीं।
(iii) विक्षेप चित्रों की सहायता से इस बात का भी ज्ञान होता है कि सहसम्बन्ध धनात्मक है या ऋणात्मक।
दोष (Demerits)-(i) विक्षेप चित्र सहसम्बन्ध के गुणांक का पूरा माप नहीं है।
(ii) यह सम्बन्धों के बारे में अनुमानतः ज्ञान देता है।
(iii) यह संख्यात्मक परिवर्तन को संख्या में ही प्रदर्शित करता है।
प्रश्न 4. पद विचलन विधि से । ज्ञात कीजिये।
(Calculater by using step deviation method.)

उत्तर-माना A = 100, h = 10. B = 1700 तथा k = 100

प्रश्न 5. कार्ल पियरसन के सहसम्बन्ध गुणांक की प्रत्यक्ष विधि से गणना करने की प्रक्रिया में कौन-कौन से चरण निहित हैं ?
(What steps are involved in the procedure of calculating Karl Pearson’s co-effecient of correlation by direct methods ?)
उत्तर-(i) सबसे पहले x और Y श्रेणी का माध्य मूल्य ज्ञात करें।
(ii) फिर X श्रेणी के मूल्यों का उसी श्रेणी के समान्तर माध्य से विचलन लें और विचलनों को x से प्रकट करें।
(iii) इसके बाद Y श्रेणी के मूल्यों का उसी श्रेणी से समान्तर माध्य से विचलन लें और विचलनों को Yसे प्रकट करें।
(iv) अब इन विचलनों का वर्ग लें।
(v) X तथा Y का गुणनफल लें और गुणनफल को XY से प्रकट करें।
(vi) सहसम्बन्ध गुणांक करने के लिये निम्न सूत्र का प्रयोग करें :
r=ΣΧΥ/√Σχ².£y²
अथवा, r=ΣΧΥ/NÓX × ÓY
x=X-X
y=Y-Y
ax = x श्रेणी का प्रमाप विचलन
Óy = y श्रेणी का प्रमाप विचलन
N= मदों की
प्रश्न 6. पिताओं (X) और उनके पुत्रों (Y) के कदों का माप नीचे इंचों में दिया गया है। इन दोनों के बीच सहसम्बन्ध गुणांक को परिकलित कीजिए।
उत्तर-सहसम्बन्ध की गणना

Rk=1-6£D²/N(N²-1)=. 1-6×22.50/8(64-1)
=1-6×22.50/8×6.3
=1-135/504=1-0.305=0.695
प्रश्न 7. वास्तविक समान्तर माध्य से कार्ल पियरसन के सहसम्बन्ध के गुणांक की गणना करें।
(Calculate the Karl Person’s coefficient correlation by the actual mean method.)

उत्तर-
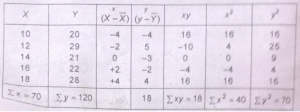
X=£X/N=70/5=14
Y= ΣY/N =120/5 =24
r=£XY/√£X²£Y²
=18/√40×70
=18/291
=34
सहसम्बन्ध निम्न धनात्मक है।
प्रश्न 8. दो शृंखलाएँ हैं। प्रत्येक के 50 पद हैं । उनका प्रमाप विचलन क्रमश: 4.5 और 3.5 है । दोनों श्रृंखलाओं के वास्तविक माध्य से विचलनों का गुणनफल 420 है । X और Y सहसम्बन्ध गुणांक ज्ञात कीजिये। 1
उत्तर-दिया है N = 50
ÓX= 4.5
Óу = 3.5
£dxdy= 420
r =£dxdy/NÓX ×ÓY
=420/50×4.5×3.5
=420×10×10/50×45×35= 533
प्रश्न 9.xऔर Y के बीच में निम्नलिखित समंकों से सह-सम्बन्ध गुणांक ज्ञात करें-
(i) X श्रेणी का समान्तर माध्य = 15
(ii) Y श्रेणी का समान्तर माध्य = 28
(iii) X श्रेणी के समान्तर माध्य से विचलनों के वर्गों का योग = 144
(iv) Y श्रेणी के समान्तर माध्य से विचलनों के वर्गों का योग = 225
(v) x वY श्रेणियों के समान्तर माध्य से विचलनों के गुणनफल का योग = 20
(vi) मदों की संख्या
उत्तर-दिया हुआ है।
x = 15
y = 28
£X² = 144
£Y²= 225
XY=20
N=10
r=£XY/√£X²×Y³
=20/√144×√225
=20/12×15=20/180=1/9=0.111
प्रश्न 10. निम्न समंको से कार्ल पियरसन का सहसम्बन्ध गुणांक ज्ञात कीजिए-
(Calculating Kari Person’s co-efficient of correlation with the help of following data)
उत्तर-कार्ल पियरसन के सहसम्बन्ध गुणांक की गणनाः
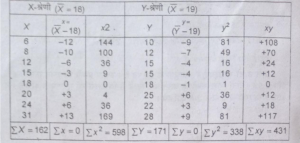
X =£X/N =162/9=18
Y=£XY/N
r=£xy/√£x² × £y²
=√431/598×338
=431/449.582
=0.050
प्रश्न 11. वास्तविक समान्तर माध्य से कार्ल पियरसन के सहसम्बन्ध के गुणांक की गणना करें।
(Calculate the Karl Person’s co-efficient of correlation by the actual mena method.)
उत्तर-
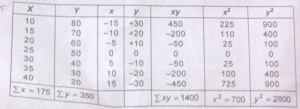
X=£X/N=175/N =25
Y=£Y/N=350/7= 50
r=£xy/£x² ×£y²=-1400/1400=-1
सहसम्बन्ध पूर्णतया ऋणात्मक है।
प्रश्न 12. कल्पित माध्य से कार्ल पियरसन के सहसम्बन्ध गुणांक की गणना करें।
(Calculate the Karl Pearson’ correlation coefficient by the assumed mean method.)
उत्तर-कार्ल पियरसन सहसम्बन्ध गुणांक
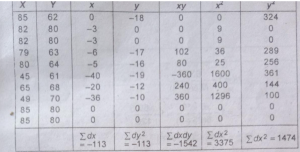
x का कल्पित माध्य = 85
yका कल्पित माध्य =80
dx dy-£dx dy/N
r = √£dx²-(£dx)²/N ×√£dy²-(£dy)²/N
r=1542-113×92/10/√£dx²-(113/
=1542-1039.6/√3247.3√1389.4
=502.4/56.9×37.2= 502.4/2116.7=2
प्रश्न 13.A तथा 8 में कोटि सहसम्बन्ध ज्ञात करें।

उत्तर-

rk=1-6£D²/N(N²-1)
= 1-6×10/5(25-1)= 1-60/120
=1-05-0.5 उत्तर ।
प्रश्न 14.A तथा B के बीच कोटि सहसम्बन्ध ज्ञात करें।

उत्तर-यहाँ पर A तथा B के कोटि क्रम दिये गये हैं। अत: हम सीधे ही कोटि क्रम का अन्तर निकालेंगे और सूत्र की सहायता से A तथा B के बीच कोटि सहसम्बन्ध की गणना करेंगे।

rk=1-6£D²/N(N²-1) =1-6×14/5(25-1) =1-84/120
=1-07 उत्तर
प्रश्न 15. X तथा Y के बीच सहसम्बन्ध गुणांक को परिकलित कीजिए तथा उनके संबंध पर टिप्पणी कीजिए।
उत्तर-

rk=1=6£D²/N(N²-1)
=1-6×14/5(25-1)
=1-6×14/5×24
=-1(84/120)=0.3
प्रश्न 16.5 विद्यार्थियों को गणित तथा अर्थशास्त्र में योग्यता के अनुसार दर्जा (Rank) दिया गया है।
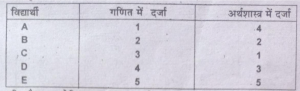
स्पीयरमैन का कोटि सहसम्बन्ध ज्ञात करें।।
उत्तर-

r=1-6£D²/N(N²-1)=1-6×0/6(36-1)
प्रश्न 17.X और Y के बीच सहसम्बन्ध गुणांक को परिकलित कीजिए और उसके सम्बन्धों पर टिप्पणी कीजिए।
उत्तर-
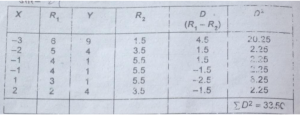
Rk=1-6£D²/N(N²-1)=1-6×33.50/6×
= 1-201/210=9/210=0.04
प्रश्न 18. दो जजों द्वारा 5 व्यक्तियों को सौंदर्य में निम्नलिखित कोटियाँ दी गई हैं। कोटि सहसम्बन्ध ज्ञात करें।
उत्तर-कोटि सहसम्बन्ध की गणना-

rk=1-6£D²/N(N²-1) =1-6×14/5(25-1)=1-84/120=1-.
प्रश्न 19.A तथा C द्वारा 5 व्यक्तियों को निम्न कोटियाँ दी गई हैं । कोटि सहसम्बन्ध की गणना करें।
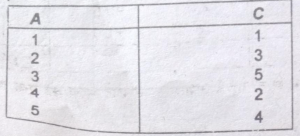
उत्तर-कोटि सहसम्बन्ध की गणना-
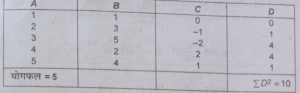
rk=1-6£D²/N(N²-1)=1-6×10/5(25-
प्रश्न 20. यदि D² = 39.50 और N = 10 हो तो Rका मूल्य ज्ञात करें।
उत्तर-r=1-6£D²/N(N²-1)
=1-6×39.50/10(10²-1)=1-6×39.5/
=1-2370/990=1-237/990=753/990=
प्रश्न 21. निम्नलिखित आंकड़ों से कोटि सहसम्बन्ध गुणांक की गणना करें-
(Calculate the co-efficient of rank correlation from the following data.).
उत्तर-
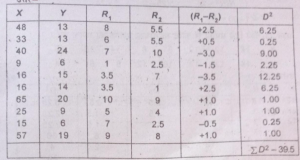
(नोट : कोटि बढ़ते हुए क्रम से दी गई है अर्थात् सबसे छोटे मूल्य को एक तथा सबसे बड़े मूल्य को दस।)

प्रश्न 22. नीचे 5 विद्यार्थियों के द्वारा अर्थशास्त्र और सांख्यिकी में प्राप्त अंक प्रतिशत में दिये गये हैं। कोटि सहसम्बन्ध ज्ञात करें।
(Below are given the percentage of marks secured by 5 students in Economics and Statics. Calculate rank correlation.)
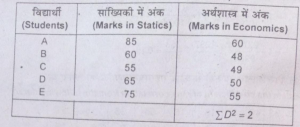
rk=1-6£D²/N(N²-1)
=1-6×12/5(25-1)
=1-6×12/5×24
=1-.06=.06
प्रश्न 23. नीचे दिये सर्पकों से कोटि सहसम्बन्ध गुणांक की गणना करें ।
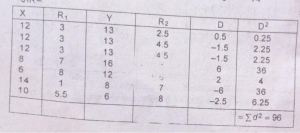
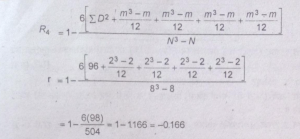
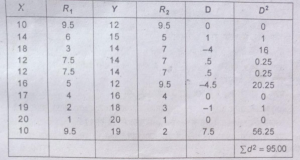
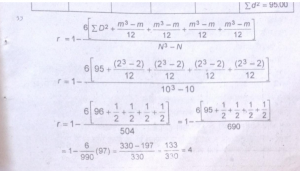
प्रश्न 24. कोटि सहसम्बन्ध गुणांक की गणना करें।
उत्तर-
वस्तुनिष्ठ प्रश्न
(Objectiver Type Questions)
प्रश्न 1. कद (फूटों में ) तथा वजन (कि० ग्राम) के बीच सहसम्बन्ध गुणांक की इकाई है-
(क) कि. ग्राम/पुट
(ख) प्रतिशत
(ग) अविद्यमान
उत्तर-कद (फूटों में) तथा वजन (किग्रा०) के बीच सहसम्बन्ध गुणांक की इकाई अविद्यमान है।
प्रश्न 2. सरल सहसम्बन्ध गुणांक का परास निम्नलिखित होगा-
(क) 0 से अनन्त तक
(ख)-1 से +1 तक
(ग) ऋणात्मक अनन्त से धनात्मक अनन्त तक
उत्तर-सरल सहसम्बन्ध गुणांक का परास -1 तथा +1 के बीच है।
प्रश्न 3. यदि rv धनात्मक है तो x और y के बीच का संबंध इस प्रकार का होता है-
(क) जब y में बढ़ता है, तो x बढ़ता है
(ख) जब y में घटता है, तो x बढ़ता है
(ग) जब y में बढ़ता है, तो x नहीं बदलता
उत्तर-यदि ru धनात्मक है तो x और y के बीच का सम्बन्ध इस प्रकार का होता है जब y में बढ़ता है, तो x बढ़ता है।
प्रश्न 4. यदिrxy= 0 है तब चर x तथा y के बीच :
(क) रैखिके संबंध होगा
(ख) रैखीय संबंध नहीं होगा
(ग) स्वतंत्र संबंध होगा
उत्तर-यदि rsy = 0 है तब चर x तथा y के बीच स्वतंत्र होगा।
प्रश्न 5. निम्नलिखित तीन मापों में, कौन सा माप किसी भी प्रकार के संबंध की माप सकता है-
(क) कार्ल पियरसन सहसम्बन्ध
(ख) स्पीयरमैन का कोटि सहसम्बन्ध
(ग) प्रकीर्ण आरेख
उत्तर- प्रकीर्ण आरेख सभी प्रकार के सम्बन्धों को माप सकता है।
प्रश्न 6. यदि परिशुद्ध रूप से मापित आँकड़े उपलब्ध हों तो सरल महासंबंध गुणांक-
(क) कोटि सहसम्बन्ध गुणांक से अधिक सही होता है।
(ख) कोटि सहसम्बन्ध गुणांक से कम सही होता है।
(ग) कोटि सहसम्बन्ध की ही भाँति सही होता है।
उत्तर-यदि परिशुद्ध रूप से मापित आँकड़े उपलब्ध हों, तो सरल सहसम्बन्ध गुणांक कोटि सहसम्बन्ध गुणांक से अधिक सही होता है।
