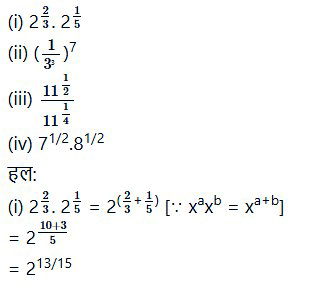BIHAR BOARD CLASS 9TH MATH | संख्या पद्धति
BIHAR BOARD CLASS 9TH MATH | संख्या पद्धति
Bihar Board Solutions for Class 9 Maths Chapter 1 Number systems (संख्या पद्धति)
प्रश्नावली 1.1
प्रश्न 1.
क्या शून्य एक परिमेय संख्या है? क्या इसे आप के रूप में लिख सकते हैं, जहाँ p और q पूर्णांक है और q ≠ 0 है?
उत्तर:

प्रश्न 2.
3 और 4 के बीच में छ: परिमेय संख्याएँ ज्ञात कीजिए।
उत्तर:
3 और 4 के बीच में छः परिमेय संख्याएँ जात करने के लिए हमें संख्याओं को, (6 + 1) अर्थात् 7 हर लेकर लिखना होगा।

प्रश्न 3.
और
के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिए।
उत्तर:

प्रश्न 4.
नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए :
(i) प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।
(ii) प्रत्येक पूर्णाक एक पूर्ण संख्या होती है।
(iii) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती है।
हल :
(i) क्योंकि सभी प्राकृत संख्याएँ {1, 2, 3, 4, ….}, पूर्ण संख्याओं {0, 1, 2, 3, 4, ….} में समाहित हैं। अतः कथन सत्य है।
(ii) क्योंकि ऋणात्मक पूर्णाक, पूर्ण संख्याओं में समाहित नहीं है। अतः कथन असत्य है।
(iii) क्योंकि परिमेय संख्याओं के संग्रह में भिन्ने एवं दशमलव संख्याएँ होती हैं जो पूर्ण संख्याओं के संग्रह में समाहित नहीं हैं। अतः कथन असत्य है।
प्रश्नावली 1.2
प्रश्न 1.
नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए :
(i) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
(ii) संख्या रेखा का प्रत्येक बिन्दु √m के रूप का होता है जहाँ m एक प्राकृत संख्या है।
(iii) प्रत्येक वास्तविक संख्या एक अपरिमेय होती है।
हल :
(i) क्योंकि वास्तविक संख्याओं का संग्रह परिमेय और अपरिमेय संख्याओं से मिलकर बना है अतः प्रत्येक अपरिमेय संख्या वास्तविक होती है। अत: कथन सत्य है।
(ii) यदि m एक प्राकृतिक संख्या है तो संख्या रेखा पर केवल 1, 2, 3, 4,……. बिन्दु ही स्थित होने चाहिए।
जबकि संख्या रेखा पर दो क्रमिक संख्याओं के मध्य अनन्त “संख्याएँ होती हैं। अत: कथन असत्य है।
(iii) क्योंकि वास्तविक संख्याओं के संग्रह में परिमेय और अपरिमेय दोनों प्रकार की संख्याएँ होती हैं। अत: प्रत्येक वास्तविक संख्या का अपरिमेय होना आवश्यक नहीं है। अतः कथन असत्य है।
प्रश्न 2.
क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं? यदि नहीं, तो एक ऐसी संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या है।
हल :
नहीं, सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय नहीं होते हैं।
उदाहरणार्थ : √9 = 3 एक परिमेय संख्या है।
प्रश्न 3.
दिखाइए कि संख्या रेखा पर √5 को किस प्रकार निरूपित किया जा सकता है?
उत्तर:
∵ “हम जानते हैं.
![]()
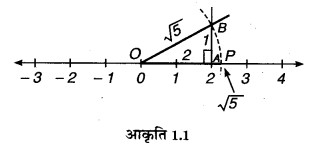
समकोण ΔOAD इस प्रकार बनाते हैं कि
OA = 2 इकाई, AB = 1 इकाई तथा ∠OAR = 90° पाइथागोरस प्रमेय से,
OB² = OA² + AB²
= 2² + 1²
= 4 + 1 = 5
⇒ OB = √5
अब, O को केन्द्र मानकर तथा OB = √5 की त्रिज्या लेकर एक चाप बनाते हैं जो संख्या रेखा को बिन्दु पर प्रतिच्छेद करता है।
अतः बिन्दु P. √5 को प्रदर्शित करता है।
प्रश्न 4.
कक्षा के लिए क्रियाकलाप (वर्गमूल सर्पिल की रचना) कीजिए।
उत्तर:
कागज की एक बड़ी शीट लीजिए और नीचे दी गई विधि से “वर्गमूल सर्पिल’ (square root spiral) की रचना कीजिए।

सबसे पहले एक बिन्दु O लीजिए और एकक सम्बाई का रेखाखण्ड (line segment) OP1 खौथिए। एकक सम्बाई वाले OP1 पर लम्ब रेखाखण्ड P1P1 खोचिए (देखिए आकृति 1.2)। अब OP1 पर साम्ब रेखाखण्ड P2P3 खोचिए। तब OP3 पर लाग्य रेखाखण्ड P3P4 खाँचिए।
इस प्रक्रिया को जारी रखते हुए 0Pn-1 पर एकक लम्बाई वाला लम्ब रेखाखण्ड खाँचकर आप रेखाखण्ड Pn-1Pn प्राप्त कर सकते हैं। इस प्रकार आप बिन्दु O, P1, P2, P3……, Pn….. प्राप्त कर लेंगे और उन्हें मिलाकर √2, √3, √4… को दर्शाने वाला एक सुन्दर सर्पिल प्राप्त कर लेंगे।
प्रश्नावली 1.3
प्रश्न 1.
निम्नलिखित भिन्नों को दशमलव रूप में लिखिए और बताइए कि प्रत्येक का दशमलव प्रसार किस प्रकार का है-




प्रश्न 2.

प्रश्न 3.


प्रश्न 4.
0.99999…. को के रूप में व्यक्त कीजिए। क्या आप अपने उत्तर से आश्चर्यचकित हैं? अपने अध्यापक और कक्षा के सहयोगियों के साथ उत्तर की सार्थकता पर चर्चा कीजिए।
हल:
माना
x = 0.99999
वहाँ एक अंक को पुनरावृत्ति है अत: 10 से गुणा करने पर,
10x = 99999
इसलिए 10 = 9 + 0-999…… 9 + x
अतः 9x = 9
अर्थात् x = 9/9 = 1
हाँ, हम अपने उत्तर से आश्चर्यचकित है।
प्रश्न 5.
के दशमलव प्रसार में अंकों के पुनरावृत्ति खण्ड में अंकों की अधिकतम संख्या क्या हो सकती है? अपने उत्तर की जाँच करने के लिए विभाजन-क्रिया कीजिए।
हल:
में हर 17 है। अत: भाग करने पर 1 से 16 तक की कोई भी संख्याएँ शेषफल के रूप में प्राप्त हो सकती है। उसके उपरान्त अंकों की पुनरावृत्ति अवश्य होगी।
अतः के दशमलव प्रसार के पुनरावृत्ति खण्ड में अधिकतम अंक = 16

16 अंकों का पुनरावृत्ति खण्ड है।
प्रश्न 6.
, q ≠ 0 के रूप में परिमेय संख्याओं के अनेक उदाहरण लीजिए, जहाँ p और q पूर्णांक हैं, जिनका 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखण्ड नहीं है और जिसका सांत दशमलव निरूपण (प्रसार) है। क्या आप यह अनुमान लगा सकते हैं कि q को कौन-सा गुण अवश्य सन्तुष्ट करना चाहिए?
हल :
के रूप में परिमेय संख्याओं का दशमलव प्रसार सांत तभी होगा जब p को qसे भाग देने पर शेषफल शून्य हो। जबकि p और g में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड न हो जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।
किसी संख्या को भाग करने पर शेषफल शून्य तभी होगा जबकि
(1) भाजक 2 या 2 की कोई घात हो।
(2) भाजक 5 या 6 की कोई घात हो।
(3) भाजक 2 की किसी घात और 5 की किसी घात का गुणनफल हो।
अतः q को 2 अथवा 5 अथवा इनकी किसी घात के बराबर होना चाहिए अथवा 2 की किसी घात और 5 की किसी घात के गुणन के बराबर होना चाहिए।
अर्थात q = 2m x 5n जहाँ m और n पूर्ण संख्याएँ हैं।
प्रश्न 7.
ऐसी तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हो।
हल :
सभी अपरिमेय संख्याओं के दशमलव प्रसार अनवसानी अनावर्ती होते हैं।
ऐसी तीन संख्याएँ √2, √3, √5 हैं।
प्रश्न 8.
परिमेय संख्याओं और
के बीच की तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।
उत्तर:
अपरिमेय संख्या ज्ञात करने के लिए सर्वप्रथम तथा
का दशमलव रूप ज्ञात करना पड़ेगा।

अपरिमेय संख्याएँ होगी।
0.7407404074000740000…
0.781078100781000…
0.803800380003800003…
प्रश्न 9.
बताइए कि निम्नलिखित संख्याओं में कौन-कौन सी संख्याएँ परिमेय और कौन-कौन भी संख्याएँ अपरिमेय हैं :

प्रश्नावली 1.4
प्रश्न 1.
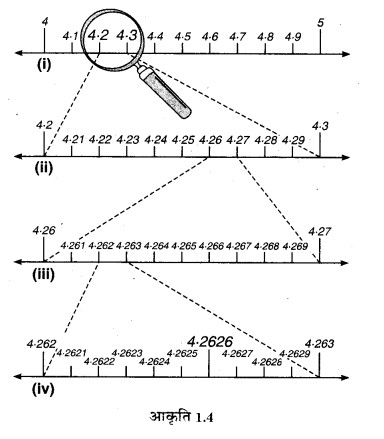
उत्तरोत्तर आवर्धन करके संख्या रेखा पर 3.765 को देखिए।
हल:
हम जानते है कि 3.765 संख्या और 4 के बीच स्थित है। आतः हम और 4 के बीच संख्या रेखा को 10 बराबर भागों में नौटते है और इस भाग के प्रत्येक बिन्दुको अंकित करते है, जैसा आकृति 1.30 में दिखाया गया है। अब 3.765 संख्या 3.7 और 3.8 के बीच स्थित है। अत: हम 3.7 और 3.8 के बीच संख्या रेखा को आवर्धन शीशे का प्रयोग करके पनः 10 बराबर भागों में बाँटते और इस भाग के प्रत्येक बिन्दु को अंकित करते है.जय पाना चिहको निरूपित करेगा दसरा चिड1.72 को निरूपित करेगा, आदि-आदि, जैसा आकृति 1.3 (ii) में दिखाया गया है। आय 3.765 पुन: 3.76 और 3.77 के बीच स्थित है। इसलिए अब संख्या रेखा के इस भाग पर अपना ध्यान केन्द्रित करते हैं आकृरि 1.3 (ii) में और कल्पना करें कि यह भाग 10 बराबर भागों में बाँटा गया है। इसे स्पष्ट रूप से देखने के लिए आवधित करते है, जैसा अकृति 1.3 (iii) में दिखाया गया है, जहाँ पहला चिह्न 3.761 को निरूपित करेगा, दूसरा चिह्न 3.762 को निरूपित करेगा, आदि-आदि। अत: 3.765 इस उपविभाजन का पांचवा चिह्न है। एक आवर्धन शीशे की सहायता से हम इसे देख सकते हैं।
इस तरह हमने यह देखा कि पर्याप्त रूप से उत्तरोत्तर आवर्धन द्वारा सांन दशमलव वाले प्रसार बाली वास्तविक संख्या को संख्या रेखा र स्थिति (या निरूपण) को स्पष्ट रूप से देखा जा सकता है।

प्रश्न 2.

प्रश्नावली 1.5
प्रश्न 1.
बाइए नीचे दी गई संख्याओं में कौन-कौन परिमेय है और कौन-कौन अपरिमेय हैं?

प्रश्न 2.
निम्नलिखित व्यंजकों में से प्रत्येक व्यंजक को सरल कीजिए
(i) (3 +√3) (2 + √2)
(ii) (3 + √3) (3 – √3)
(iii) (√5 + √2)²
(iv) (√5 – √2) (√5 + √2).
हल:
(i) (3 +√3) (2 + √2)
= 3 × 2 + 2 × √3 + √2 × 3 + √3 × √2
= 6 + 2√3 + 3√2 + √6.
(ii) (3 + √3) (3 – √3)
= 3² – (√3)²
= 9 – 3 = 6.
(iii) (√5 + √2)²
= (√5)² + (√2)² + 2 × √5 × √2
= 5 + 2 – 2√10 = 7 + 2√10.
(iv) (√5 – √2) (√5 + √2) = (√5)² – (√2)²
= 5 – 2 = 3.
प्रश्न 3.
आपको याद हगा कि। को एक वृत्त की परिधि (मान लीजिए और उसके व्यास (मान लीजिए d) के अनुपात से परिभाषित किया जाता है, अर्थात् π = c/d है। यह इस तथ्य का अंतर्विरोध करता हुआ प्रतीत होता है कि अपरिमेय है। इस अंतर्विरोध का निराकरण आप किम प्रकार करेंगे?
उत्तर:
स्पष्ट है कि c/d = c/d , π का एक निकटतम मान है, जो कि दो संख्याओं के अनुपात से प्राप्त हुआ है।
तथा पूँकि π एक अपरिमेय संख्या है।
अत: यह इस तथ्य का विरोध नहीं है।
प्रश्न 4.
संख्या रेखा पर √9.3 को निरूपित कीजिए।
हल:
एक दो हुई रेला पर एक स्थिर विन्दु A से 9.3 एकक की दरी पर चिर लगएँ तथा उस विन्द को B मान लें, जिससे कि AB = 9.3 एकक B से। एकक की दूरी पर चिड़ लगाइए और इस नए बिन्दूको मान लीजिए। AC का मध्य बिन्द ज्ञात कीजिए और उसे 0 मान लीजिए। अब०को केन्द्र और.cकोत्रिज्या मानकर एकअर्धवनचनाहएI AC केबिन्द B पर एक लम्ब रेखा खींची जो अर्डवत को D पर काटती हो, तर BD = √9.3 है।

अब बिन्दु B को केन्द्र व BD को त्रिज्या मानकर एक चाप खींचिए जो रेखा AB को आगे बढ़ाने पर E पर काटती है. अतः अब BE संख्या रेला परा √9.3 को निरुपित करेगा और यदि B का मान शून्य लें तो E = √9.3 निरूपित होगा।
प्रश्न 5.
निम्नलिखित केहरों का परियकरण कीजिए
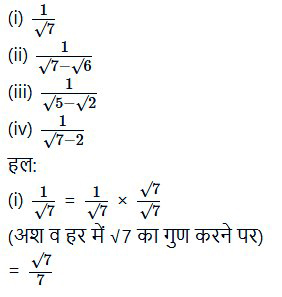

प्रश्नावली 1.6
प्रश्न 1.
ज्ञात कीजिए :


प्रश्न 2.
ज्ञात कीजिए।


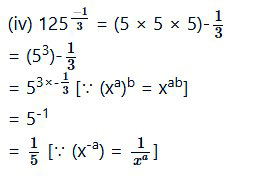
प्रश्न 3.
सरल कीजिए :