BIHAR BOARD CLASS 9TH MATH | समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
BIHAR BOARD CLASS 9TH MATH | समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
Bihar Board Solutions for Class 9 Maths Chapter 9 Area of Parallelograms and Triangles (समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल)
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
प्रश्नावली 9.1
1. निम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समांतर
रेखाओं के बीच स्थित हैं ? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समांतर रेखाएँ
लिखिए।
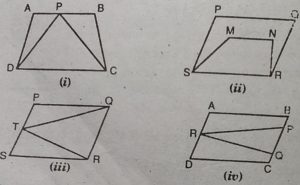
हल : दी गई आकृतियाँ समान आधार और समान समांतर रेखाओं के मध्य, जैसा कि उनके प्रति संकेत किया गया है, पर स्थित हैं:
(i) आधार DC, समांतर रेखाएँ DC और AB
(iii) आधार QR, समांतर रेखाएँ QR और PS.
(v) आधार AD, समांतर रेखाएँ AD और BQ.
प्रश्नावली 9.2
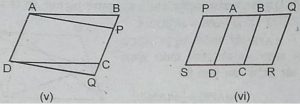
1. आकृति में, ABCD एक समांतर चतुर्भुज है,
AE⊥DC और CF⊥AD है। यदि AB = 16
cm, AE=8 cm और CF = 10 cm है, तो AD
ज्ञात कीजिए ।
हल : हम जानते हैं,
समांतर चतुर्भुज का क्षेत्रफल = आधार x ऊँचाई
.: समांतर चतुर्भुज ABCD का क्षेत्रफल = ABX AE=(16×8) cm²
= 128 cm² …(1)
साथ ही, समांतर चतुर्भुज ABCD का क्षेत्रफल = ADx CF
= (ADx 10) cm² …(2)
समी. (1) व (2) से, 128 = ADx 10
⇨ AD = 128/10 cm = 12.8cm
2. यदि E, F, G और H क्रमशः समांतर चतुर्भुज ABCD की भुजाओं के मध्य-बिंदु हैं, तो दर्शाइए कि ar (EFGH) = 1/2 ar (ABCD) है।
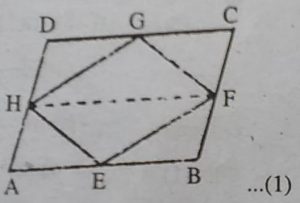
हल : ∆ HGF और समांतर चतुर्भुज HDCF
समान आधार HF और समान समांतर रेखाओं
HF और DC के मध्य स्थित हैं।
ar(HGF)=1/2 ar(HDCF) ….(1)
इसी प्रकार, ∆ HEF और समांतर चतुर्भुज ABFH समान आधार HF और समान समांतर रेखाओं HF और AB के मध्य स्थित हैं।
.: ar(HEF) = 1/2 ar(ABFH) ….(2)
.: समी. (1) व (2) को जोड़ने पर,
ar(HGF)+ ar(∆HEF) =1/2[ar(HDCF)+ ar(ABFH)]
⇨ ar(EFGH) = 1/2 ar(ABCD).
3. Pऔर Q क्रमशः समांतर चतुर्भुज ABCD की भुजाओं DC तथा AD पर स्थित बिन्दु हैं। दर्शाइए कि ar (APB) = ar(BQC) है।

हल : ∆APB और समांतर चतुर्भुज ABCD
समान आधार AB और समान समांतर रेखाओं
AB और DC के मध्य स्थित हैं।
.: ar(APB) = 1/2 ar(ABCD) …(1)
इसी प्रकार, A BQC और समांतर चतुर्भुज ABCD समान आधार BC और समान समांतर रेखाओं BC तथा AD के मध्य स्थित हैं।
.: ar(BQC)= 1/2 ar(ABCD) …(2)
समी. (1) व (2) से,
ar (APB) = ar (BQC).
4. आकृति में, Pसमांतर चतुर्भुज ABCD के अभ्यंतर
में स्थित कोई बिन्दु है । दर्शाइए कि
(i) ar (APB) + ar(PCD)= 1/2 ar(ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)


हल : EPF रेखा को AB या DC के समांतर
खींचिए और GPH को AD या BC के समांतर
खींचिए।
अब AGHD एक समांतर चतुर्भुज है
[चूँकि GH||DA और AG || DH]
इसी प्रकार, HCBG, EFCD तथा ABFE समांतर
चतुर्भुज हैं।
(i) ∆APB और समांतर चतुर्भुज ABFE समान आधार AB पर और समान समांतर रेखाओं AB और DC के मध्य स्थित हैं।
.: ar(APB) = 1/2 ar(ABFE) ….(1)
इसी प्रकार, ar(PCD) = 1/2 ar(EFCD) …(2)
समी. (1) व (2) को जोड़ने पर,
ar(APB) + ar(PCD) = 1/2[ar(ABFE) + ar(EFCD)]
= 1/2 ar(ABCD) …(3)
(ii) ∆APD और समांतर चतुर्भुज AGHD समान आधार AD पर और समान समांतर रेखाओं AD और HG के मध्य स्थित हैं।
.: ar(APD) = 1/2 ar(AGHD) ….(4)
इसी प्रकार, ar(PCD) = 1/2 ar(GBCH) …(5)
समी. (4) व (5) को जोड़ने पर,
ar(APD) + ar(APCD) = 1/2[ar(AGHD)+ar(GBCH)]
= 1/2 ar(ABCD) …(6)
समी. (5) व (6) से,
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
5. आकृति में, PQRS और ABRS समांतर चतुर्भुज हैं तथा X भुजा BR पर स्थित कोई बिन्दु है। दर्शाइए कि
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2 ar (PQRS)

हल : (i) समांतर चतुर्भुज PQRS और समांतर
चतुर्भुज ABRS समान आधार RS और समान
समांतर रेखाओं SR और PAQB के बीच स्थित हैं।
.: ar (PQRS) = ar (ABRS) ….(1)
(ii) ∆AXS और समांतर चतुर्भुज ABRS समान आधार AS और समान समांतर रेखाओं AS और RB के मध्य स्थित हैं।
.: ar(AXS)= 1/2 ar(ABRS)
⇨ ar(AXS) = 1/2 ar(PQRS) [सेमी. (1) के प्रयोग से]
6. एक किसान के पास समांतर चतुर्भुज PQRS के रूप का एक खेत था। उसके RS पर स्थित कोई बिन्दु A लिया और उसे PऔरQ से मिला दिया। खेत कितने भागों में विभाजित हो गया है ? इन भागों के आकार क्या हैं ? वह किसान खेत में गेहूँ और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहता है। वह ऐसा कैसे करे?

हल : स्पष्टतः, खेत अर्थात समांतर चतुर्भुज PQRS तीन भागों में विभाजित हो गया है। प्रत्येक भाग त्रिभुजाकार है।
चूँकि ∆APQ और समांतर चतुर्भुज PQRS समान
आधार PQ और समान समांतर रेखाओं PQ और
SR के मध्य स्थित हैं।
.: ar(APQ) = 1/2 ar(PQRS) ….(1)
स्पष्ट रूप से,
ar(APS) + ar(AQR) = ar (PQRS) – ar(APQ)
= ar(PQRS) – 1/2 ar(PORS) [समी. (1) के प्रयोग से]
= 1/2 ar(PQRS) ….(2)
समी. (1) व (2) से, ar (APS) + ar(AQR) = ar(APQ).
अत: किसान गेहूँ और दालों को या तो [(∆S APS तथा AQR) या ∆APQ या ∆APQ या ∆APS तथा ∆AQR की भांति बोए।
प्रश्नावली 9.3
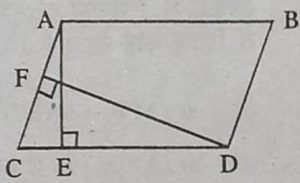
1. आकृति में, ∆ABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है। दर्शाइए कि
ar(ABE) = ar(ACE) है।
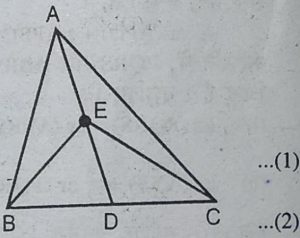
हलः दिया है : AD त्रिभुज ABC की माध्यिका
है और E भुजा AD पर स्थित कोई बिंदु है।
सिद्ध करना है : ar(ABE) = ar(ACE)
प्रमाण : चूँकि AD त्रिभुज ABC की माध्यिका है
.: ar(ABD) = ar(ACD) …(1)
साथ ही, ED त्रिभुज EBC की माध्यिका है
.: ar (BED) = ar(CED) ….(2)
समी. (2) से सेमी. (1) घटाने पर,
ar(ABD)-ar(BED) = ar(ACD)-ar(CED)
⇨ ar(ABE) = ar(ACE).
2. ∆ABC में, E माध्यिका AD का मध्य-बिंदु है । दर्शाइए कि ar(BED)
= 1/4ar(ABC) है।
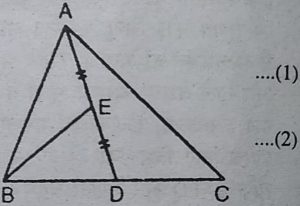
हल : दिया है : एक ∆ABC है, E माध्यिका AD का मध्य-बिंदु है।
सिद्ध करना है : ar(BED) = 1/4ar(ABC).
प्रमाण : चूँकि AD त्रिभुज ABC की माध्यिका है और माध्यिका एक त्रिभुज को दो समान क्षेत्रफलों वाले त्रिभुजों में विभाजित करती है।
.: ar(ABD) = ar(ADC)
⇨ ar(ABD) = Par(ABC) ….(1)
∆ABD में, BE माध्यिका है
.: ar(BED) = ar(BAE) ….(2)
⇨ ar(BED) = 1/2 ar(ABD)
⇨ ar(BED) = 1/2×1/2ar(ABC) [समी. (1) के प्रयोग द्वारा]
⇨ ar(BED)= 1/4 ar(ABC).
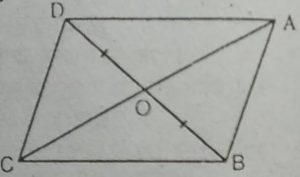
3. दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
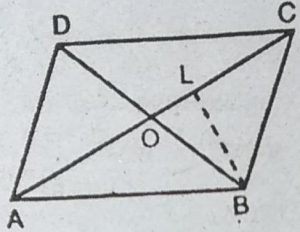
हल : समांतर चतुर्भुज ABCD दिया है।
सिद्ध करना है : विकर्ण AC और BD समांतर चतुर्भुज ABCD को समान क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
रचना : BL⊥AC खींचें।
सिद्ध प्रमाण : चूँकि ABCD एक समांतर चतुर्भुज है, अत: इसके विकर्ण AC और BD एक-दूसरे को O बिंदु पर काटते हैं।
AO = OC और BO = OD
अब, ar(AOB) = 1/2 ×AO× BL
ar(OBC)= 1/2 OC× BL
परंतु AO = OC
.: ar(AOB) = ar(OBC)
इसी प्रकार, हम दर्शा सकते हैं कि
ar(OBC) = ar(OCD); ar(OCD) = ar(ODA):
ar(ODA) = ar(OAB) ; ar(OAB) = ar(OBC)
ar(OCD) = ar(ODA)
इस प्रकार ar(OAB) = ar(OBC) = ar(OCD) = ar(OAD).
4. आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं । यदि रेखाखंड CD रेखाखंड AB से बिन्दु 0 पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD) है।
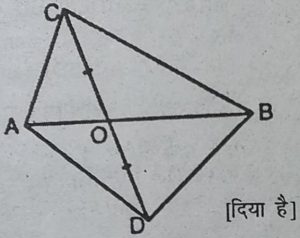
हल : दिया है : दो त्रिभुज ABC और ABD एक
ही आधार AB पर स्थित हैं। रेखाखंड CD को AB
बिंदु O पर समद्विभाजित करती है, अर्थात OC = OD है।
सिद्ध करना है : ar(ABC) = ar(ABD).
प्रमाण : ∆ACD में,
OC = OD [दिया है।]
.: AO एक माध्यिका है
.: ar(AOC) = ar(AOD)
[चूँकि माध्यिका किसी त्रिभुज को दो समान क्षेत्रफलों वाले त्रिभुजों में बाँटती है]
इसी प्रकार, ∆BCD में BO माध्यिका है
ar(BOC) = ar(BOD) …(2)
समी. (1) व (2) को जोड़ने पर,
ar(AOC)+ ar(BOC) = ar(AOD) + ar(BOD)
⇨ ar(ABC) = ar(ABD).
5. D,E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु हैं। दर्शाइए कि
(i) BDEF एक समांतर चतर्भुज है
(ii) ar(DEF) = 1/4 ar(ABC)
(iii) ar(BDEF) = 1/2ar(ABC)
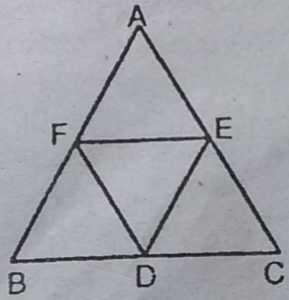
हल : दिया है : D,E और F क्रमश: ∆ABC की
भुजाओं BC, CA और AB के मध्य-बिन्दु हैं।
सिद्ध करना है : (i) BDEF एक समांतर चतुर्भुज है।
(ii) ar(DEF) =1/4ar(ABC)
(iii) ar(BDEF) =1/2ar(ABC)
प्रमाण (i) ∆ABC में,
EF || BC [मध्य-बिंदु प्रमेय द्वारा, चूँकि E और F
क्रमश: AC और AB के मध्य बिंदु हैं।]
.: EF || BD … (1)
साथ ही ED || AB [मध्य-बिंदु प्रमेय द्वारा, चूँकि E और D
क्रमश: AC और BC के मध्य-बिदु हैं।]
ED || AF …(2)
समी. (1) और (2) से, BDEF एक समांतर चतुर्भुज है।
(ii) इसी प्रकार, FDCE और AFDE समांतर चतुर्भुज हैं
.: ar(FBD) = ar(DEF) [चूँकि FD समांतर चतुर्भुज BDEF का एक विकर्ण है]
ar(DEC) = ar(DEF) [ED समांतर चतुर्भुज FDCE का विकर्ण है।]
और ar(AFE) = ar(DEF) [चूँकि FE समांतर चतुर्भुज AFDE का एक विकर्ण है।]
.: ar(FBD) = ar(DEC) = ar(AFE) = ar(DEF) …(3)
⇨ ar(DEF) = 1/4ar(ABC)
(iii) साथ ही,
ar(BDEF) = 2 ar(DEF)
=2×1/4 ar(ABC) = 1/2ar(ABC).
6. आकृति में, चतुर्भुज ABCD के विकर्ण AC
और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद
करते हैं कि OB=OD है । यदि AD = CD है,
तो दर्शाइए कि
(i) ar(DOC) = ar(AOB)
(ii) ar(DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है।
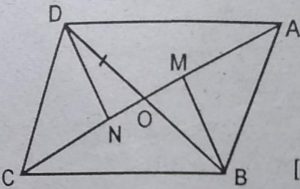
हल : (i) DN⊥AC और BM⊥AC की रचना कीजिए।
∆DON और ∆BOM में,
∠DNO = ∠BMO [प्रत्येक = 90°]
∠DON=∠BOM [उर्ध्वाधर सम्मुख कोण]
OD = OB [दिया है।]
सर्वांगसम की AAS रचना द्वारा
∆DON ≈ ∆BOM …(1)
DCN और ∆BAM में,
∠DNC = ∠BMA [प्रत्येक = 90°]
DC = AB [दिया है।]
DN = BM [चूँकि ∆DON = BOM DDN = BM]
.: सर्वांगसम की RHS रचना द्वारा
∆DCN ∆BAM …(2)
समी. (1) व (2) से,
ar(DON) + ar (DCN) = ar(BOM) + ar(BAM)
ar(DOC) = ar(AOB)
(ii) चूँकि ar (DOC) = ar(ABO)
.: ar(DOC+ ar(BOC) = ar(AOB) + ar(BOC)
⇨ ar(DCB) = ar(ACB).
(iii) ∆DCB और ∆ACB के क्षेत्रफल और आधार समान हैं। अत: उनके त्रिभुज समान
समांतर रेखाओं के मध्य स्थित होंगे।
⇨ DA || CB अर्थात्, ABCD एक समांतर चतुर्भुज है।
7. बिन्दु D और E क्रमश:∆ABC की भुजाओं AB
और AC पर इस प्रकार स्थित हैं कि ar(DBC)
= ar(EBC) है। दर्शाइए कि DE || BC है।
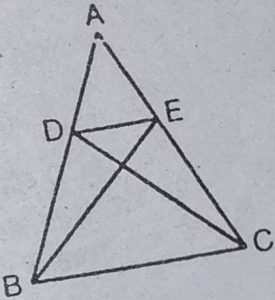
हल : चूँकि ∆DBC और ∆EBC के क्षेत्रफल समान
हैं और दोनों के आधार भी समान हैं।
.: ∆DBC की D से ऊँचाई = ∆EBC की E से ऊँचाई
⇨ ∆DBC और ∆EBC समान समांतर रेखाओं के मध्य स्थित हैं।
⇨ DE || BC.
8. XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है। यदि BE || AC और CF || AB रेखा XY से क्रमशः E और F पर मिलती हैं, तो दर्शाइए कि : ar(ABE) = ar(ACF)
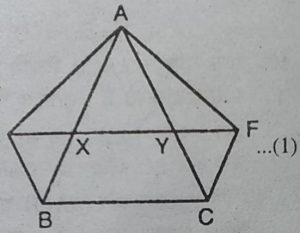
हल : चूँकि XY || BC और BE||CY
.: BCYE एक समांतर चतुर्भुज है।
चूँकि ∆ABE और समांतर चतुर्भुज BCYE समान
आधार BE और समान समांतर रेखाओं BE और
AC के मध्य स्थित हैं।
.: ar(ABE) =1/2ar(BCYE) …(1)
अब, CF || AB तथा XY || BC
⇨ CF ||AB तथा XF || BC
⇨ BCFX एक समांतर चतुर्भुज है।
चूंकि ∆ACF और समांतर चतुर्भुज BCFX समान आधार CF
और समान समांतर रेखाओं AB और FC के मध्य स्थित हैं।
.: ar(ACF) = 1/2 ar(BCFX) …(2)
लेकिन समांतर चतुर्भुज BCFX और समांतर चतुर्भुज BCYE समान आधार BC पर और
समान समांतर रेखाओं BC और EF के मध्य स्थित हैं।
.: ar(BCFX) = ar(BCYE) …(3)
समी. (1), (2) और (3) से,
ar(∆ABE) = ar(∆ACF)
9. समांतर चतुर्भुज ABCD की एक भुजा AB को
एक बिन्दु P तक बढ़ाया गया है। A से होकर
CP के समांतर खींची गई रेखा बढ़ाई गई CB को
Q पर मिलाती है और फिर समांतर चतुर्भुज
PBQR को पूरा किया गया है (देखिए आकृति)।
दर्शाइए कि ar(ABCD) = ar(PBQR) है।


हल : AC और PQ को मिलाइए। चूँकि AC और
PQ क्रमशः समांतर चतुर्भुज ABCD और समांतर
चतुर्भुज PBQR के विकर्ण हैं।
.: ar(ABC) = 1/2ar(ABCD) …..(1)
और, ar(PBQ) = 1/2ar(PBRQ) …..(2)
अब, ∆ACQ और ∆AQP समान आधार AQ
पर और समान समांतर रेखाओं AQ और CP
के मध्य स्थित हैं।
.: ar(ACQ) = ar(AQP)
⇨ar(ACQ)-ar(ABQ) = ar(AQP)-ar(ABQ) ar(ABQ)
को दोनों और से घटाने पर
⇨ ar(ABC) = ar(BPQ)
⇨ 1/2 ar(ABCD) = 1/2 ar(PBRQ) [समी. (1) व (2) के प्रयोग से]
⇨ ar(ABCD) = ar(PBRQ)
10. एक समलंब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ar(AOD) = ar (BOC) है।
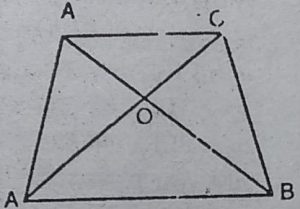
हल : समलंब ABCD में AB || DC है, के विकर्ण
AC और BC परस्पर O पर प्रतिच्छेद करते हैं।
.: ∆ABC और ∆ABD समान आधार और
समान समांतर रेखाओं के मध्य स्थित हैं।
.: ar(ABD) = ar(ABC)
⇨ ar(ABD)- ar(AOB) = ar(ABC)- ar(AOB)
[ar(AOB) को दोनों पक्षों से घटाने पर]
⇨ ar(AOD) = ar(BOC)
11. आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समांतर खींची गई रेखा बढ़ाई गई DC को F पर मिलाती है। दशाईए कि
(i) ar(ACB) = ar(ACF)
(ii) ar (AEDF) = ar (ABCDE)
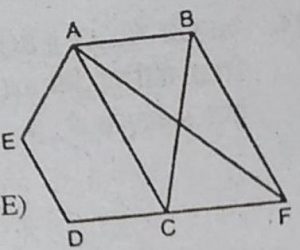
हल : (i) चूँकि ∆ACB और ∆ACF समान
आधार AC और समान समांतर रेखाओं AC
और BF के मध्य स्थित हैं।
.: ar(ACB) = ar(ACF).
(ii) ar (ACDE) को दोनों पक्षों में जोड़ने पर,
ar(ACF) + ar(ACDE) = ar(ACB) + ar(ACDE)
⇨ ar(AEDF) = ar(ABCDE).
12. गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम
पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि
वहाँ एक स्वास्थ्य केन्द का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस
प्रतिबन्ध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के
संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए । स्पष्ट
कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है ?

हल : माना ABCD एक चतुर्भुजाकार भूखंड है।
DE को E पर CA के समांतर मिलाने के लिए BA
को आगे बढ़ाएँ।
इस प्रकार, ∆EAC और ∆ADC समान समांतर
रेखाओं DE और CA के बीच स्थिति में आ जाती
हैं।
.: ar(EAC) = ar(ADC)
अब, ar(ABCD) = ar(ABC) + ar(ACD)
= ar(ABC) + ar(ADC)
= ar(ABC) + ar(EAC)
=ar(EBC)
अर्थात् चतुर्भुज ABCD=AEBC
जिसकी प्रस्तावित सुझाव की व्याख्या आवश्यक है।
13. ABCD एक समलंब है, जिसमें AB || DC है।
AC के समांतर एक रेखा AB को x पर और
BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए
कि ar(ADX) = ar(ACY) है।
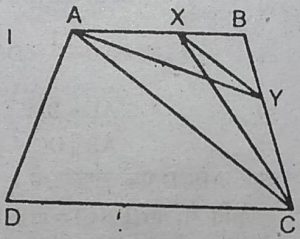
हल : ABCD एक समलंब है, जिसमें AB || DC
और XY || AC है। XC को मिलाइए।
ar(ACX) = ar(ACY) …(1)
[चूँकि ∆ACX और ACY का
आधार समान है और समान समांतर रेखाओं AC और XY के मध्य स्थित हैं।
परन्तु ar(ACX) = ar(ADX)
[चूँकि ∆ACX और ∆ADX का आधार AX समान है और दोनों
समान समांतर रेखाओं AB और DC के मध्य स्थित हैं।]
समी. (1) व (2) से,
ar(ADX) = ar(ACY).
14. आकृति में, AP || BQ || CR है।
सिद्ध कीजिए कि ar(AQC) = ar(PBR) है।
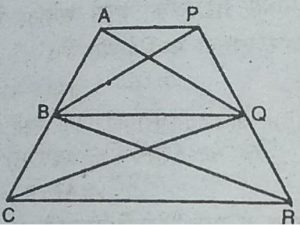
हल : आकृति से,
ar(AQC) = ar(AQB) + ar(BQC) ….(1)
और, ar(PBR) = ar(PBQ) + ar(QBR) ….(2)
लेकिन ar(AQB) = ar(PBQ) ….(3)
[ ये त्रिभुज समान आधार BQ पर और समान
समांतर रेखाओं AP और BQ के बीच स्थित हैं।]
साथ ही, ar(BQC) = ar(QBR) ….(4)
[ ये त्रिभुज समान आधार BQ पर और समान समांतर
रेखाओं BQ और CR के बीच स्थित हैं।]
समी. (3) और (4) को समी. (1) और (2) में प्रयोग करने पर, हम प्राप्त करते हैं
ar(AQC) = ar(PBR)
15. चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद
करते हैं कि ar(AOD) = ar(BOC) है । सिद्ध कीजिए कि ABCD एक समलंब है।

हल: चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते
हैं कि
ar(AOD) = ar(BOC) …(1)
ar(ODC) को दोनों पक्षों में जोड़ने पर,
ar(AOD) + ar(ODC) = ar(BOC) + ar(ODC)
ar(ADC) = ar(BDC)
1/2×DC× AL = 1/2×DC×BM
AL = BM
AB ||DC
अत: ABCD एक समलंब है।
16. आकृति में, ar(DRC) = ar(DPC) है और ar(BDP) = ar(ARC) है । दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब हैं।
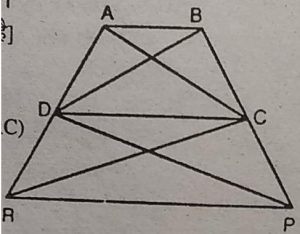
हल : आकृति में, ar(BDP) = ar(ARC) [दिया है।]
और ar(DPC) = ar(DRC) [दिया है।]
घटाने पर हम प्राप्त करते हैं
ar(BDP) -ar(DPC) = ar(ARC) – ar(DRC)
ar(BDC) = ar(ADC)
DC||AB
अत: ABCD एक समलंब है।
ar(DRC) = ar(DPC) [दिया है।]
ar(DLC) को दोनों पक्षों से घटाने पर,
ar(DRC)-ar(DLC)= ar(DPC)-ar(DLC)
⇨ ar(DLR) = ar(CLP)
ar(RLP) को दोनों पक्षों में जोड़ने पर प्राप्त होता है
ar(DLR)+ ar(RLP) = ar(CLP) + ar(RLP)
⇨ ar(DRP) = ar(CRP)
⇨ RP || DC
अत: DCPR एक समलंब है।
प्रश्नावली 9.4 (ऐच्छिक)
1. समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके
क्षेत्रफल बराबर हैं । दर्शाइए कि समांतर चतुर्भुज का परिमाप आयत के परिमाप से
अधिक है।
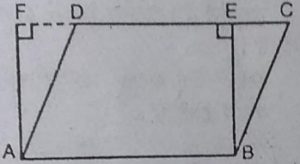
हल : दिया है : एक समांतर चतुर्भुज ABCD
और एक आयत ABEF समान आधार पर स्थित
हैं और उनके क्षेत्रफल भी समान हैं।
सिद्ध करना है : समांतर चतुर्भुज ABCD का
परिमाप > आयत ABEF का परिमाप ।
प्रमाण : चूँकि समांतर चतुर्भुज और आयत की
सम्मुख भुजाएँ बराबर होती हैं।
.: AB = DC [चूँकि ABCD एक समांतर चतुर्भुज है।]
और AB = EF [चूँकि ABEF एक आयत है]
.: DC = EF …(1)
⇨ AB + DC = AB + EF ….(2)
चूंकि दी गई रेखा के किसी बिदु से खींचे जा सकने वाले सभी खंड इस पर स्थित नहीं
हैं, अत: लंब खंड सबसे छोटा है।
.: BE<BC तथा AF <AD
⇨ BC>BE तथा AD>AF
⇨ BC + AD > BE + AF ….(3)
समी. (2) व (3) को जोड़ने पर,
AB + DC + BC + AD > AB + EF + BE + AF
⇨ AB + BC + CD + DA > AB + BE + EF+ FA
अतः समांतर चतुर्भुज ABCD का परिमाप > आयत ABEF का परिमाप ।
2. आकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित हैं कि BD = DE =
EC है। दर्शाइए कि ar(ABD) = ar(ADE) = ar(AEC) है।
क्या आप अब उस प्रश्न का उत्तर दे सकते हैं,
जो आपने इस अध्याय की ‘भूमिका’ में छोड़
दिया था कि “क्या बुधिया का खेत वास्तव में
बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो
गया है?
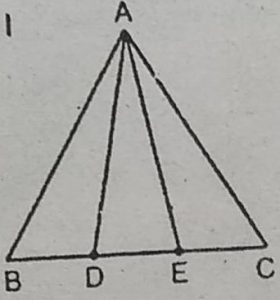
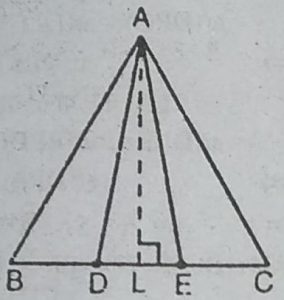
हल : माना AL रेखा BC पर लंब है, अत: AL
त्रिभुज ABD, ∆ADE और ∆AEC की ऊँचाई है।
.: ar(ABD) = 1/2×BD×AL
ar(ADE)= 1/2× DE×AL
और, ar(AEC) = 1/2× EC × AL
चूँकि BD = DE = EC
.: ar(ABD) = ar(ADE) = ar(AEC)
हाँ, सभी त्रिभुजों की ऊँचाई समान है। बुधिया इस प्रश्न के उत्तर द्वारा अपने खेत को तीन
बराबर भागों बाँट सकती है।
3. आकृति में, ABCD,DCFE और ABFE समांतर
चतुर्भुज हैं । दर्शाइए कि ar(ADE) = ar(BCF)
है।

हल : चूँकि समांतर चतुर्भुज की सम्मुख भुजाएँ
बराबर होती हैं।
.: AD = BC [ चूँकि ABCD एक समांतर चतुर्भुज है]
DE = CF [चूँकि DCFE एक समांतर चतुर्भुज है।]
और, AE = BF [चूँकि ABFE एक समांतर चतुर्भुज है]
∆ADE और ∆BCF पर विचार कीजिए, जिनमें AE = BE, AD = BC और DE = CF
.: सर्वांगसम की SSS रचना द्वारा
∆ADE ∆BCF
⇨ ar(ADE) = ar(BCF)
4. आकृति में, ABCD एक समांतर चतुर्भुज है और
BC को एक बिन्दु तक इस प्रकार बढ़ाया गया
है कि AD=CQ है । यदि AQ भुजा DC को P
पर प्रतिच्छेद करती है, तो दर्शाइए कि ar(BPC)
= ar(DPQ) है।

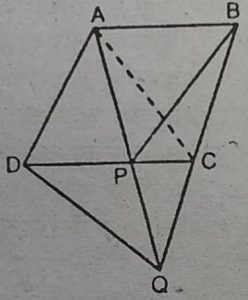
हल : AC को मिलाइए।
चूंकि ∆APC और ∆BPC एक ही आधार PC पर तथा समान समांतर रेखाओं PC और AB
के मध्य स्थित हैं।
.: ar(APC) = ar(BPC) ….(1)
चूंकि AD =CQ
और AD||CQ [दिया है।]
.: चतुर्भुज ADQC में, सम्मुख भुजाओं का
एक युग्म बराबर और समांतर है।
.: ADQC एक समांतर चतुर्भुज है।
⇨ AP = PQ और CP = DP
[चूँकि समांतर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।]
∆APC और ∆DPQ में,
AP = PQ [ऊपर सिद्ध है।]
∠APC = ∠DPQ [उर्ध्वाधर सम्मुख कोण]
और, PC = PD [ऊपर सिद्ध है।]
.: सर्वांगसम की SAS रचना द्वारा
∆APC≈∆DPQ
⇨ ar(APC) = ar(DPQ) [चूँकि सर्वांगसम त्रिभुजों का क्षेत्रफल समान होता है]
.: ar(BPC) = ar(DPQ)
5. आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का
मध्य बिन्दु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि
(i) ar(BDE) = 1/2ar(ABC)
(ii) ar(BDE)= 1/2ar(BAE)
(iii) ar(ABC) = 2 ar(BEC)
(iv) ar(BFE) = ar(AFD).
(v) ar(BFE) = 2 ar(FED)
(vi) ar(FED)= 1/8ar(AFC)

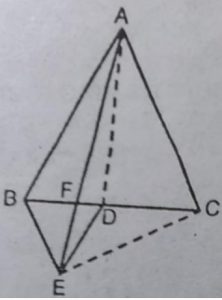
हल : EC और AD को मिलाइए।
माना ∆ABC की भुजा a है। तब,
ar(ABC) = √3/4a²=∆
(i) ar(BDE) = √3/4(a/2)²
[ BD= 1/2 BC=a/2] = √3/16 a² = ∆/4
⇨ ar(BDE) = 1/4 ar(ABC).
(ii) हमें ज्ञात है,
ar(BDE) = 1/2ar(BEC) …. (i)
[चूँकि DE,∆BEC की माध्यिका है और प्रत्येक माध्यिका
किसी त्रिभुज को दो समान क्षेत्रफल के त्रिभुजों में बाँटती है]
अब, ∠EBC=60°
और ∠BCA=60°
⇨ ∠EBC=∠BCA.
लेकिन ये रेखाखंड BE और CA तथा उनकी तिर्यक रेखा BC से संबद्ध एकांतर कोण हैं।
अतः BE||AC.
अब ∆ BEC और ∆ BAE समान आधार BE और समान समांतर रेखाओं BE और AC
के मध्य स्थित हैं।
.: ar(BEC) = ar(BAE)
.: समी. (1) से,
ar(ABDE)= 1/2ar(BAE).
(iii) चूँकि ED त्रिभुज BEC की एक माध्यिका है और हम जानते हैं कि प्रत्येक माध्यिका किसी त्रिभुज को दो समान क्षेत्रफल वाले त्रिभुजों में बाँटती है।
.: ar(BDE) = 1/2ar(BEC)
भाग (i) से, ar(BDE) = 1/4ar(ABC)
इन परिणामों को जोड़ने पर, हम प्राप्त करते हैं
1/4ar(ABC)= 1/2ar(BEC)
⇨ ar(ABC) = 2ar(BEC).
(iv) अब, ∠ABD=∠BDE= 60° [दिया है।]
लेकिन ∠ABD तथा ∠BDE रेखा खण्ड BA तथा DE उनका तिर्यक रेखा BD से संबद्ध एकातर कोण हैं।
अत: BA|| ED.
अब, ∆BDE तथा ∆AED समान आधार ED पर तथा समान समांतर रेखाओं BA तथा DE के बीच स्थित हैं।
.: ar(BDE) = ar(AED)
⇨ ar(BDE) – ar(FED) = ar(AED) – ar(FED)
⇨ ar(BEF) = ar(AFD)
(v) In∆ABC, AD² = AB²-BD²
= a²-a²/4=3a²/4
⇨ AD = √3/2a
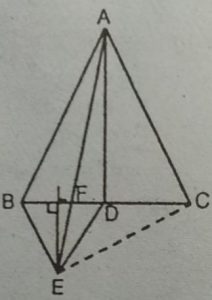
∆ BED में, EL² = DE² -DL²
⇨ EL = √3a/4
.: ar(AFD) =1/2× FD×AD
= 1/2 ×FD × √3/2a ….(1)
और ar(EFD) = 1/2×FD×EL
= 1/2× FD = √3/4a …(2)
(1) तथा (2) से, हमें ar(AFD) = 2ar (EFD) प्राप्त होता है
इस परिणाम को भाग (iv) में प्रयोग करने पर हमें
ar (BFE) = ar (AFD)
= 2ar (EFD) प्राप्त होता है
(iv) भाग (i) से ar (BDE) = 1/4ar(ABC)
⇨ ar (BEF) + ar (FED) = 1/4×2ar (ADC)
⇨ 2ar (FED) + ar(FED) = 1/2ar (AFC) -ar (AFD))
[भाग (v) का प्रयोग करने पर]
⇨ 3ar (FED) = 1/2ar(AFC)-1/2×2ar(FED)
⇨ 4ar (FED) = 1/2ar (AFC)
⇨ ar(FED) = 1/8ar(AFC)
6. चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते हैं। दर्शाइए कि ar(APB) × ar(CPD) = ar(APD) ×ar(BPC) है।
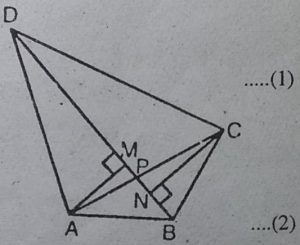
हल : चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु P पर प्रतिच्छेद करते हैं।
AM ⊥ BD और CN ⊥ BD खींचिए ।
अब, ar(APB) × ar(CPD)
=(1/2 ×BP×AMr)×(1/2×DP×CN)
= 1/4×BP×DP×AM×CN ….(1)
और, ar(APD) × ar(BPC)
=(1/2×DP×AM)×(1/2×BP×CN)
= 1/4×BP×DP×AM×CN …..(2)
समी. (1) और (2) से,
ar(APB)×ar(CPD) = ar(APD) × ar(BPC)
7. P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु हैं तथा
बिंदु R रेखाखंड AP का मध्य-बिन्दु है । दर्शाइए कि :
(1) ar(PRO) = 1/2 ar(ARC)
(ii) ar(RQC) = 3/8 ar(ABC)
(iii) ar(PBQ) = ar(ARC)
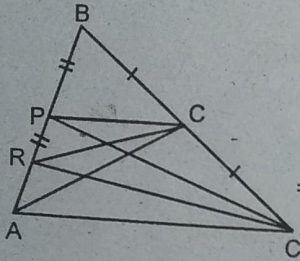
हल : P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु हैं।
AQ और PC को मिलाइए।।
(i) हमारे पास है,
ar(PQR) = 1/2ar(APQ)
[चूँकि QR त्रिभुज APQ की माध्यिका है और यह त्रिभुज को दो
समान क्षेत्रफलों वाले त्रिभुजों में बाँटती है]
= 1/2 ar(ABQ)
[चूँकि QP त्रिभुज ABQ की माध्यिका है।]
= 1/4ar(ABQ)=1/4×1/2 ar(ABC)
[चूँकि AQ त्रिभुज ABC की माध्यिका है।]
= 1/8ar(ABC) ….(1)
पुनः ar(ARC) = 1/2ar(APC)
[चूँकि CR त्रिभुज APC की माध्यिका है।]
= 1/2×1/2ar(ABC)
[चूँकि CP त्रिभुज ABC की माध्यिका है।]
= 1/4ar(ABC ) …. (2)
समी. (1) और (2) से,
ar(PQR) = 1/8ar(ABC)
=1/2×1/4ar(ABC) = 1/2ar(ARC).
(ii) हमारे पास है,
ar(RQC) = ar(RQA) + ar(AQC)- ar(ARC) ….(3)
अब, ar(∆RQA) = 1/2ar(PQA)
[चूँकि RQ,∆PQA की माध्यिका है।]
= 1/2×1/2(AQB)
[चूँकि AQ त्रिभुज AQB की माध्यिका है।]
= 1/4ar(AQB) = 1/4×1/2ar(ABC)
[चूँकि AQ, ∆ABC की माध्यिका है।]
= 1/8ar(ABC) ….(4)
ar(AQC) = 1/2ar(ABC) ….(5)
[चूँकि AQ, ∆ABC की माध्यिका है]
अथवा, (∆ ARC = 1/2ar(APC) [चूँकि CR,∆APC की माध्यिका है]
= 1/2×1/2 ar(ABC) [चूँकि CP,∆ABC की माध्यिका है]
= 1/4ar(ABC) ….(6)
समी. (3), (4), (5) और (6) से,
ar (RQC) = 1/8ar(ABC) + 1/2ar(ABC) – 1/4ar(ABC)
= (1/8+1/2-1/4)ar(ABC) = 3/8ar(ABC).
(iii) हमारे पास है,
ar(PBQ) = 1/2ar(ABQ) [ चूँकि PQ, त्रिभुज ABQ की माध्यिका है]
= 1/2×1/2ar(ABC) [चूँकि AQ, त्रिभुज ABC की माध्यिका है]
= 1/4ar(ABC) = ar(ARC). [समी. (6) से]
8. आकृति में, ABC एक समकोण त्रिभुज है
जिसका कोण A समकोण है। BCED,
ACFG और ABMN क्रमशः भुजाओं BC,
CA और AB पर बने वर्ग हैं। रेखाखंड AX ⊥DE
भुजा BC को बिन्दु Y पर मिलाता है।
दर्शाइए कि:
(i) ∆MBC ≈∆ABD
(ii) ar(BYXD)=2 ar(MBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) ∆ FCB≈∆ACE
(v) ar(CYXE) = 2ar(FCB)
(vi) ar(CYXE) = ar(ACFG)
(vii)ar(BCED)=ar(ABMN) + ar(ACFG)
टिप्पणी : परिणाम (vii) प्रसिद्ध (सुपरिचित) पाइथागोरस प्रमेय है। इस प्रमेय की एक सरलतम उपपत्ति आप कक्षा X में पढ़ेंगे।
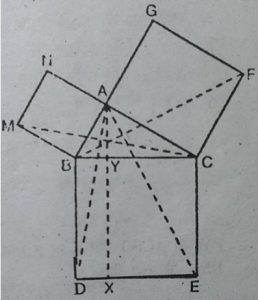
हल : (i)∆MBC और ∆ABD में,
BC = BD [वर्ग BCED की भुजाएँ।]
MB = AB [वर्ग ABMN की भुजाएँ।]
∠MBC = ∠ABD [चूँकि प्रत्येक = 90° + ∠ABC]
.: सर्वांगसम की SAS रचना द्वारा,
∆MBC≈ ∆ABD
(ii) ∆ABD और वर्ग BYXD समान आधार BD और समान समांतर रेखाओं BD और
AX के मध्य स्थित है।
.: ar(ABD) = 1/2ar(BYXD)
लेकिन ∆MBC ∆ABD [भाग (i) में सिद्ध]
⇨ ar(MBC) = ar(ABD)
.: ar(MBC) = ar(ABD) = 1/2ar(BYXD)
⇨ ar(BYXD) = 2 ar(MBC)
(iii) वर्ग ABMN और MBC समान आधार MB और समान समांतर रेखाओं MB
और NAC के बीच स्थित हैं।
.: ar(MBC) =1/2ar(ABMN)
⇨ ar(ABMN) = 2ar(MBC)
= ar(BYXD) [भाग (ii) के प्रयोग से]
(iv) ∆ACE और ∆ BCF में,
CE = BC [वर्ग BCED की भुजाएँ।]
AC = CF [वर्ग ACFG की भुजाएँ।]
और ∠ACE = ∠BCF [चूँकि प्रत्येक = 90° + ∠BCA]
.: सर्वांगसम की SAS रचना द्वारा,
∆ACEE ∆BCF
(v) ∆ACE और वर्ग CYXE समान आधार CE और समान समांतर रेखाओं CE और
AYX बीच स्थित हैं।
.: ar(ACE) = 1/2ar(CYXE)
⇨ ar(FCB) = 1/2ar(CYXE) ) [चूँकि ∆AC≈ ∆BCF, भाग (iv)]
⇨ ar(CYXE) =2ar(FCB).
(vi) वर्ग ACFG और ∆BCF सामान आधार CF और समान समांतर रेखाओं CF और BAG के मध्य स्थित हैं।
.: ar(BCF) = 1/2ar(ACFG)
⇨ 1/2ar(CYXE) = 1/2ar(ACFG) [भाग (v) के प्रयोग से]
⇨ ar(,CYXE)= ar(ACFG)
(vii) भाग (iii) और (vi) से,
ar(BYXD) = ar(ABMN)
और, ar(CYXE) = ar(ACFG)
जोड़ने पर,
ar(BYXD) + ar(CYXE) = ar(ABMN) + ar(ACFG)
ar(BCED) = ar(ABMN) + ar(ACFG).
***
