BIHAR BOARD CLASS 9TH MATH | त्रिभुज
BIHAR BOARD CLASS 9TH MATH | त्रिभुज
Bihar Board Solutions for Class 9 Maths Chapter 7 Triangles (त्रिभुज)
त्रिभुज
प्रश्नावली 7.1
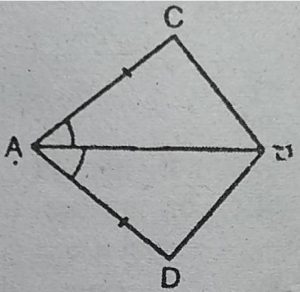
1. चतुर्भुज ACBD में, AC=AD है और AB कोण A
को समद्विभाजित करता है (देखिए आकृति)।
दर्शाइए कि ∆ABC ≈ ∆ABD है।
BC और BD के बारे में आप क्या कह सकते हैं ?
हल : अब ∆ABC और ∆ABD में,
AC = AD [दिया है।]
∠CAB = ∠BAD [ चूंँकि AB कोण A को समद्विभाजित करता है।]
और AB = AB [उभयनिष्ठ है।]
.: भुजा कोण भुजा सर्वांगसमता गुण धर्म से
∆ABC≈∆ABD
⇨ BC = BD
[चूंँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।]
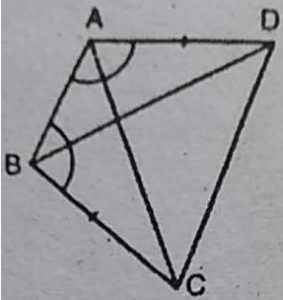
2. ABCD एक चतुर्भुज है, जिसमें AD = BC
और ∠DAB = ∠CBA है (आकृति देखें)।
सिद्ध कीजिए कि
(i) ∆ABD≈∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
हल : त्रिभुज ∆ABD तथा ∆BAC में,
AD = BC [दिया है।]
∠DAB = ∠CBA [दिया है।]
AB = AB [उभयनिष्ठ]
.: भुजा कोण भुजा सर्वांगसमता गुणधर्म से,
∆ABD≈∆BAC [जिससे सिद्ध होता है।
⇨ BD = AC
और, ∠ABD =∠BAC
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।]
3. एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दर्शाइए कि CD, रेखाखंड AB को समद्विभाजित करता है।

हल : क्योंकि AB और CD, O पर प्रतिच्छेद करते हैं। इसलिए,
∠AOD = ∠BOC ….(1) [शीर्षाभिमुख कोण]
∆AOD और ∆BOC में,
∠AOD = ∠BOC [1 से]
∠DAO = ∠OBC [प्रत्येक 90°]
और AD = BC [दिया है।
अब कोण, कोण, भुजा सर्वांगसम गुणधर्म से,
∆AOD≈ ∆BOC
⇨ OA = OB
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।]
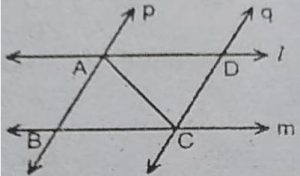
4. l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है ( देखिए आकृति)।
दर्शाइए कि ∆ARC ≈∆CDA है।
हल : चूँकि l तथा m समांतर रेखाएँ दूसरी समांतर
रेखाओं p और q द्वारा प्रतिच्छेदित की जाती हैं। अत:
AD || BC तथा AB ||CD
⇨ ABCD समांतर चतुर्भुज हैं।
अत: AB = CD और BC = AD
अब ∆ABC और ∆CDA में,
AB = CD [ऊपर प्रमाणित किया गया है।]
BC = AD [ऊपर प्रमाणित किया गया है।]
तथा AC = AC [उभयनिष्ठ]
.: भुजा, भुजा, भुजा सर्वांगसमता गुणधर्म से,
∆ABC≈∆CDA.
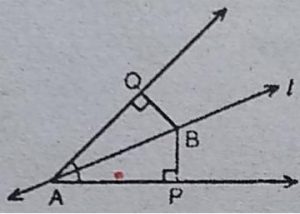
5. रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिन्दु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लम्ब हैं
(देखिए आकृति)।
दर्शाइए कि:
(i) ∆APB ≈ ∆AQB
(ii) BP = BQ है, अर्थात् बिन्दु B कोण की भुजाओं से समदूरस्थ है।
हल : ∆APB तथा ∆AQB में,
∠APB = ∠AQB [चूँकि प्रत्येक = 90°]
∠PAB = ∠QAB [चूँकि AB, LPAQ को समद्विभाजित करती है।]
AB = AB [उभयनिष्ठ]
कोण, कोण-भुजा सर्वांगसमता गुणधर्म से,
∆APB≈∆AQB [जो कि प्रमाणित करता है।]
⇨ BP = PQ
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं]
अत: B, ∠A की भुजाओं से समदूरस्थ है।
6. आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है।
दर्शाइए कि BC = DE है।

हल : ∆ABC तथा ∆ADE में,
AB = AD [दिया है।]
∠BAC = ∠DAE
चूँकि ∠BAD = ∠EAC
⇨ ∠BAD + ∠DAC = ∠EAC + ∠DAC
और ∠BAC = ∠DAE [दिया है।]
.: भुजा कोण भुजा सर्वांगसम गुणधर्म से,
∆BAC≈ ∆DAE
और AC= AE [दिया है।]
भुजा कोण भुजा सर्वांगसम गुणधर्म से,
∆ABC ≈∆ADE ⇨BC = DE
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।]
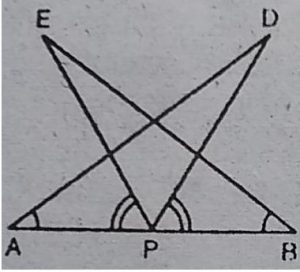
7. AB एक रेखाखंड है और P इसका मध्य-बिन्दु है । D और E रेखाखंड AB के एक ही ओर स्थित दो बिन्दु इस प्रकार हैं कि ∠BAD = ∠ABE
और ∠EPA = ∠DPB हैं। (देखिए आकृति)। दर्शाइए कि
(i) ∆DAP≈ ∆EPB (ii) AD = BE
हल: ∠EPA = ∠DPB
⇨ ∠EPA+ ∠DPE = ∠DPB+ ∠DPE
⇨ ∠DPA = ∠EPB …..(1)
अब, ∆EBP तथा ∆DAP में,
∠EPB =∠DPA [1 से]
BP = AP [दिया है।]
और ∠EBP = ∠DAP [दिया है।]
अतः कोण भुजा कोण सर्वांगसमता गुणधर्म से
∆EBP≈ ∆DAP
⇨ BE = AD अत: AD = BE
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।]
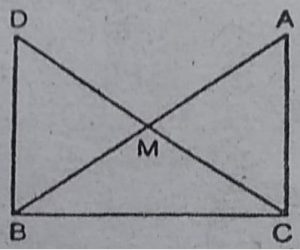
8. एक समकोण त्रिभुज ABC में कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर बिन्दु D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है ( देखिए आकृति)। दर्शाइए कि
(i) ∆MCE ∆BMD
(ii) ∠DBC एक समकोण है
(iii) ∆DBC = ∆ACB
(iv) CM = 1/2 AB
हल : (i) ∆AMC तथा ∆BMD में,
AM = BM [ चूँकि M, AB का मध्य बिन्दु है]
∠AMC = ∠BMD [शीर्षाभिमुख कोण है]
और, CM = MD [दिया गया है]
.: भुजा कोण भुजा सर्वांगसमता गुणधर्म से
∆AMC ≈ ∆BMD
(ii) अब, ∆AMC≈ ∆BMD ⇨ BD = CA
और ∠BDM = ∠ACM …..(1)
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं]
इसीलिए, तिर्यक रेखा CD,CA तथा BD को C तथा D पर क्रमशः इस प्रकार काटती
है कि एकान्तर कोण ∠BDM = ∠ACM | अत: BD || CA.
⇨ ∠CBD+ ∠BCA = 180°
[चूँकि तिर्यक रेखा के एक ही ओर के आंतरिक कोणों का योग 180° होता है।]
⇨ ∠CBD+ 90° = 180° [चूँकि ∠BCA = 90°]
⇨ ∠DBC = 90°
(iii) अब ∆DBC तथा ∆ACB में,
BD = CA [1 से]
∠DBC = ∠ACB [प्रत्येक = 90°]
BC = BC [उभयनिष्ठ]
.: भुजा कोण भुजा सर्वांगसम गुणधर्म से,
∆DBC≈ ∆ACB
(iv) CD = AB
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।
⇨1/2CDA = 1/2 AB ⇨ CM = 1/2 AB
प्रश्नावली 7.2
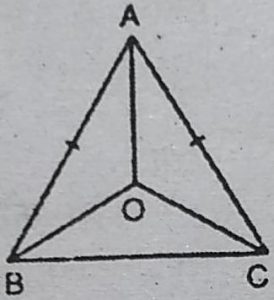
1. एक समद्विबाहु त्रिभुज ABC जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेद करते हैं। A और O को जोड़िए । दर्शाइए कि
(i) OB= OC (ii)AO कोण A को समद्विभाजित करता है।
हल: (i) ∆ABC में, AB = AC
⇨ ∠B= ∠C
[चूँकि बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
⇨ 1/2 ∠B = 1/2 ∠C
⇨ ∠OBC = ∠OCB ….(1)
[चूँकि OB तथा OC क्रमशः ∠B तथा ∠C को काटते हैं।]
.: ∠OBC = 1/2 ∠B और ∠OCB = 1/2 ∠C
⇨ OB = OC …..(2)
[चूँकि समान कोणों के सम्मुख भुजाएँ समान होती है।]
(ii) अब ∆ABO तथा ∆ACO में,
AB = AC [दिया है।]
∠OBC = ∠OCB [समीकरण 1 से]
OB = OC [समीकरण 2 से]
.: भुजा कोण भुजा सर्वांगसमता गुणधर्म से,
∆ABO ≈∆ACO
⇨ ∠BAO = ∠CAO
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।]
⇨ AO, ∠BAC को समद्विभाजित करता है।
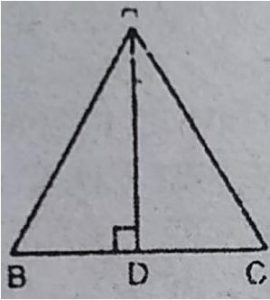
2. ∆ABC में AD भुजा BC का लम्ब समद्विभाजक है। (देखिए आकृति)। दर्शाइए
कि ∆ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
हल : ∆ABD तथा ∆ACD में,
DB = DC [दिया है।]
∠ADB = ∠ADC [ चूँकि AD⊥ BC]
AD = AD [उभयनिष्ठा]
.: भुजा कोण भुजा सर्वांगसमता गुणधर्म से,
∆ABD ≈ ∆ACD
⇨ AB = AC [चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।]
अत: ∆ABC समद्विबाहु त्रिभुज है।
3. ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर शीर्षलम्ब
क्रमशः BE और CF खींचे गए हैं। (देखिए आकृति)। दर्शाइए कि ये शीर्षलम्ब
बराबर हैं।
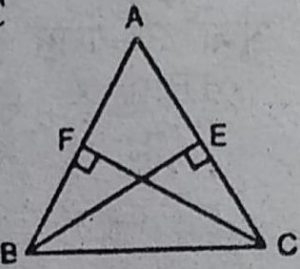
हल : माना कि BE ⊥ AC तथा CF ⊥ AB
∆ABE तथा ∆ACF में, ∠AEB = ∠AFC [चूँकि प्रत्येक =90°]
∠A = ∠A [उभयनिष्ठ]
तथा AB = AC [दिया है।]
.: कोण कोण भुजा सर्वांगसमता गुणधर्म से,
∆ABE≈ ∆ACF
⇨ BE = CF
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।
अत: शीर्षलम्ब बराबर हैं।
4. ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलम्ब BE और CF
बराबर हैं (देखिए आकृति)। दर्शाइए कि
(i) ∆ABE ≈ ∆ACF (ii) AB = AC, अर्थात् ∆ ABC समद्विबाहु त्रिभुज है।
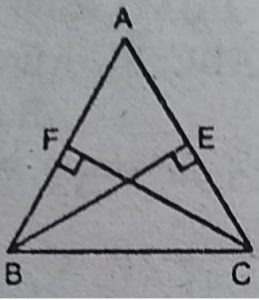
हल : ∆ABE तथा ∆ACF में,
∠AEB = ∠ACF [चूँकि प्रत्येक = 90°]
∠BAE = ∠CAF [उभयनिष्ठ]
तथा BE = CF [दिया है।]
.: कोण-कोण-भुजा सर्वांगसमता गुणधर्म से,
(i) ∆ABE≈ ∆ACF
⇨ AB = AC [चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।]
(i) अत: ∆ABC एक समद्विबाहु त्रिभुज है।
5. ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु
त्रिभुज हैं ( देखिए आकृति)। दर्शाइए कि :
∠ABD = ∠ACD है।
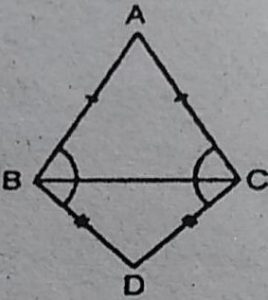
हल : ∆ ABC में, AB = AC
⇨ ∠ABC = ∠ACB ….(1)
[चूँकि समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
∆BCD में, BD = CD
⇨ ∠DBC = ∠DCB ….(2)
[चूँकि समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
समीकरण (1) तथा (2) को जोड़ने पर,
∠ABC + ∠DBC = ∠ACB + ∠DCB
⇨ ∠ABD = ∠ACD
6. ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिंदु D तक इस प्रकार बढ़ाई गई है कि AD = AB है ( देखिए आकृति)। दर्शाइए कि ∠BCD एक समकोण है।

हल : ∆ABC में, AB = AC [दिया है।]
∠ACB = ∠ABC …. (1)
[चूँकि समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
अब, AB = AD [दिया है।]
.: AD = AC [चूँकि AB = AC]
इसीलिए, ∆ADC में, AD = AC
⇨ ∠ACD = ∠ADC ….(2) [चूँकि समान भुजाओं के सम्मुख
कोण बराबर होते हैं।]
समीकरण (1) तथा (2) को जोड़ने पर,
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇨ ∠BCD = ∠ABC+ ∠BDC [चूँकि ∠ADC = ∠BDC]
⇨ ∠BCD+∠BCD = ∠ABC + ∠BDC + ∠BCD
[∠BCD को दोनों ओर जोड़ने पर]
⇨ 2∠BCD = 180° ⇨∠BCD = 90°
अत: ∠BCD एक समकोण है।
7. ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और
AB = AC है। ∠B और ∠C ज्ञात कीजिए।

हल : ∆ABC में, ∠A = 90°
AB = AC
⇨ ∠B = ∠C
[चूँकि समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
[कोणों के योग के नियम से]
और ∠A+∠B+∠C =180°
⇨90° +22B = 180° [चूँकि ∠C=∠B]
⇨ 2∠B = 180°-90° = 90°
⇨ ∠B = 90°/2 = 45°
.: ∠C=∠B =45°
8. दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक
कोण 60° होता है।
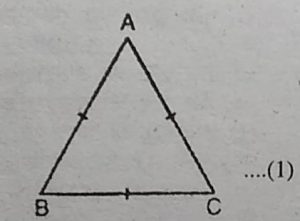
हल : माना ∆ABC एक समबाहु त्रिभुज है।
अत: AB = AC = BC
अब AB = AC
⇨ ∠B = ∠C ….(1)
[चूँकि समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
तथा CB = CA
⇨ ∠A = ∠B ….(2)
[चूँकि समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
समीकरण (1) तथा (2) से,
∠A=∠B=∠C
तथा ∠A+ ∠B+∠C = 180° [कोण-योगधर्म के अनुसार]
.: ∠A+ ∠A+∠A = 180°
⇨ 3∠A = 180°
⇨ ∠A = 60°
.: ∠A = ∠B = ∠C = 60°
अतः समबाहु त्रिभुज के सभी कोण 60° के होते हैं।
प्रश्नावली 7.3
1. ∆ABC और ∆DRC एक ही आधार पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि
A और D भुजा BC के एक ही तरफ स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने
पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि
(i) ∆ABD ≈ ∆ACD (ii) ∆ABP≈ ∆ACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखंड BC का लम्ब समद्विभाजक है।
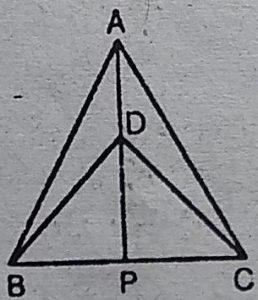
हल : (i)∆ABD तथा ∆DBC में,
AB = AC [दिया है।]
BD = DC [दिया है।]
तथा AD = AD [उभयनिष्ठ]
.: भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से,
∆ABD ≈∆ACD
(ii) ∆ABP तथा ∆ACP में,
AB= AC [दिया है।]
∠BAP = ∠PAC [ चूँकि ∆ABD ≈ ∆ACD
⇨ ∠BAD = ∠DAC
⇨∠BAP = ZPAC]
तथा AP = AP [उभयनिष्ठ]
.: भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से,
∆ABP ≈∆ACP
(iii) चूँकि ∆ABD ≈∆ACD इसलिए
∠BAD = ∠DAC
⇨ AD, ∠A को समद्विभाजित करता है।
⇨ AP, ∠A को समद्विभाजित करता है।
∆ BDP तथा ∆CDP में, ….(1)
BD = CD [दिया है।]
BP = PC [चूँकि ∆ABP ≈∆ACP ⇨ BP = PC]
तथा DP = DP [उभयनिष्ठ]
.: भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से
∆BDP ≈ ∆ PDC
⇨ DP,∠D को समद्विभाजित करता है
⇨AP, ∠A को समद्विभाजित करता है ….(2)
(1) तथा (2) को जोड़ने पर, AP, ∠A तथा ∠D को समद्विभाजित करता है
(iv) चूँकि AP, BC पर स्थित है
.: ∠APB+ ∠APC = 180° [समांतर युग्म]
लेकिन ∠APB = ∠APC [ऊपर सिद्ध किया गया है।]
.: ∠APB = ∠APC = 180°/2 = 90°
एवम् BP = PC [ऊपर सिद्ध किया गया है।]
⇨ AP, BC का लम्ब समद्विभाजक है।
2. AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB= AC है । दर्शाइए कि
(i) AD रेखाखंड BC को समद्विभाजित करता है।
(ii) AD कोण A को समद्विभाजित करता है।

हल : AD, शीर्ष A से डाला हुआ लम्ब है जो कि समद्विबाहु ∆ABC के आधार BC के सम्मुख है। AB = AC, ∠ADC = ∠ADB = 90°
अब ∆ADB तथा ∆ADC में,
कर्ण AB = कर्ण AC [दिया है।]
AD = AD [उभयनिष्ठ]
तथा ∠ADC = ∠ADB [ चूँकि प्रत्येक = 90°]
.: समकोण, कर्ण, भुजा सर्वांगसमता गुणधर्म से,
∆ADB ≈∆ADC
⇨ BD = DC तथा ∠BAC=∠DAC
[चूँकि सर्वांगसमता त्रिभुजों के संगत भाग बराबर होते हैं]
अत: AD, BC को समद्विभाजित करता है जो कि सिद्ध करता है (i) को तथा AD, ∠A को समद्विभाजित करता है जो कि (ii) को सिद्ध करता है।
3. एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः एक-दूसरे की भुजाओं PQ और QR तथा माध्यिका PN के बराबर हैं (देखिए आकृति)। दर्शाइए कि:
(i) Δ ΑΒΜ≈ Δ ΡQN
(ii) ∆ABC≈∆PQR
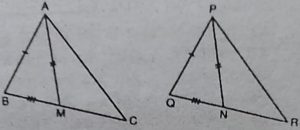
हल : ∆ABC तथा ∆PQR में,
AB = PQ
BC = QR
तथा AM = PN
चूँकि AM तथा PN क्रमश: ∆ ABC तथा ∆ PQR की माध्यिकाएँ हैं।
अब, BC = QR [दिया है।]
⇨ 1/2 BC= 1/2 QR
⇨ BM = QN ….(1)
अब, ∆ABM तथा ∆PQN में,
AB = PQ [दिया है।]
BM = QN [1 से]
तथा AM = PN [दिया है।]
.: भुजा-भुजा-भुजा सर्वांगसम गुणधर्म से,
∆ABM≈∆PQN, जो कि सिद्ध करता है (i) भाग को
⇨ ∠B = ∠Q ….(2)
[चूँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।]
अब ∆ABC तथा ∆PQR में,
AB = PQ [दिया है।]
∠B = ∠Q [(2) से]
BC = QR [दिया है।]
.: भुजा कोण भुजा सर्वांगसमता गुणधर्म से,
∆ABC ≈ ∆PQR, जो कि (ii) भाग को सिद्ध करता है।
4. BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ∆ABC समद्विबाहु त्रिभुज है।
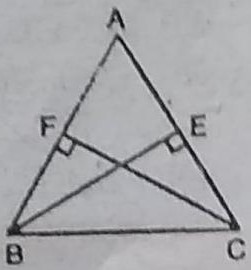
हल : ∆BCF तथा ∆CBE में,
∠BFC=∠CEB [चूँकि प्रत्येक = 90°]
कर्ण BC = कर्ण BC [उभयनिष्ठ]
FC = EB
.: समकोण, कर्ण भुजा सर्वांगसमता गुणधर्म से,
∆ BCF ∆CBE
⇨ ∠FBC = ∠ECB [चूँँकि सर्वांगसम त्रिभुज के संगत भाग बराबर होते हैं।]
.: ∆ABC एक समद्विबाहु त्रिभुज है।
5. ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है । AP ⊥ BC खींच कर दर्शाइए
कि∠B=∠C है।
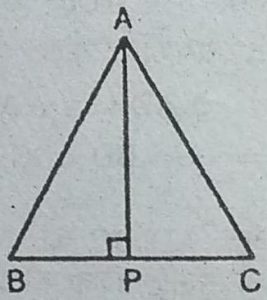
हल : ∆ABP तथा ∆ACP में,
AB = AC [दिया है।]
AP = AP [उभयनिष्ठ]
तथा ∠APB = ∠APC [चूंकि प्रत्येक = 90°]
.: समकोण, कर्ण, भुजा सर्वांगसम गुणधर्म से,
∆ABP ≈∆ACP
⇨ ∠B =∠C
[चूँँकि सर्वांगसम त्रिभुजों के संगत भाग बराबर होते हैं।
प्रश्नावली 7.4
1. दर्शाइए कि समकोण त्रिभुज में कर्ण की सबसे लंबी भुजा होती है।
हल : माना कि ∆ABC समकोण त्रिभुज है जिसमें ∠ABC = 90°
लेकिन ∠ABC+ ∠BCA + ∠CAB = 180°
⇨ 90° + ∠BCA + ∠CAB = 180°
⇨ ∠BCA+ ∠CAB = 90°
∠BCA तथा ∠CAB न्यून कोण हैं।
⇨ ∠BCA <90° तथा ∠CAB< 90°
⇨ AC>AB तथा AC> BC
[चूँँकि बड़े कोण के सम्मुख की भुजा बड़ी होती है]

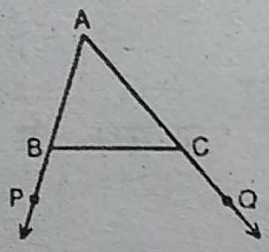
2. आकृति में ∆ABC की भुजाओं AB और AC को क्रमशः बिन्दुओं P और Q तक बढ़ाया गया है। साथ ही ∠PBC <∠QCB है। दर्शाइए कि AC>AB है।
हल : चूँँकि ∠PBC < ∠QCB
⇨ -∠PBC > -∠QCB
⇨ 180° -ZPBC > -2QCB
⇨ ∠ABC > ∠ACB
⇨ AC> AB
[चूंँकि बड़े कोण की सम्मुख भुजा बड़ी होती है।]
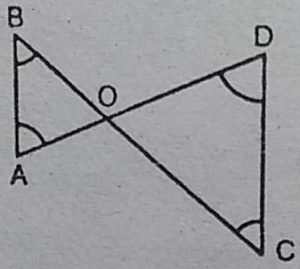
3. आकृति में, ∠B < ∠A और ∠C < ∠D है।
दर्शाइए कि AD < BC है।
हल : चूँँकि ∠B < ∠A तथा ∠C < ∠D
AO < BO तथा OD < OC
[.: बड़े कोण की सम्मुख भुजा बड़ी होती है।]
इन परिणामों को जोड़ने पर,
AO + OD < BO + OC
⇨ AD < BC
4. AB और CD क्रमशः एक चर्तुभुज ABCD की सबसे छोटी
और सबसे बड़ी भुजाएँ हैं। (देखिए आकृति)।
दर्शाइए कि ∠A > ∠C और ∠B >∠D है।

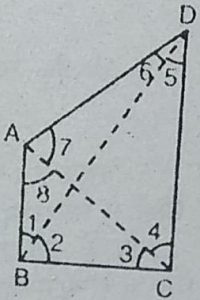
हल : ABCD एक चतुर्भुज है जिसमें AB सबसे छोटी
भुजा है तथा CD सबसे बड़ी भुजा है।
AC तथा BD को मिलाया।
चूंँकि AB, चतुर्भुज ABCD की सबसे छोटी भुजा है।
.: ∆ABC में, BC > AB
⇨ 28 > 23 …(1)
[चूंँकि बड़ी भुजा के विपरीत कोण बहा होता है।]
चूँकि CD चतुर्भुज ABCD की सबसे बड़ी भुजा है।
.: ∆ACD में, CD > AD
⇨ ∠7 > ∠4 ….(2)
[चूंँकि बड़ी भुजा की सम्मुख कोण बड़ा होता है।]
(1) तथा (2) को जोड़ने पर,
∠8+∠7 > ∠3 +∠4
⇨ ∠A > ∠C ….(3)
पुन: ∆ABD में, AD > AB [ चूंँकि AB सबसे छोटी भुजा है।]
⇨ ∠A> ∠6 …..(4)
(3) और (4) को जोड़ने पर,
∠1+∠2 > ∠5+∠6 ⇨ ∠B > ∠D
इसीलिए ∠A > ∠C और ∠B > ∠D
5. आकृति में, PR> PQ है और PS कोण QPR
को समद्विभाजित करता है। सिद्ध कीजिए कि
∠PSR > ∠PSQ है।

हल : ∆PQR में, PR > PQ [दिया है।]
⇨ ∠PQR > ∠PRQ
[चूंँकि बड़ी भुजा की सम्मुख कोण बड़ा होता है।]
⇨ ∠PQR+∠1 > ∠PRQ+∠1 [दोनों ओर 21 जोड़ने पर]
⇨ ∠PQR + ∠1 > ∠PRQ+∠2 ….(1)
[चूंँकि PS, ∠P का कोण समद्विभाजक है, .: ∠1 = ∠2]
अब ∆PQS तथा ∆PSR, में,
∠PQR+∠1+ ∠PSQ = 180°
⇨ ∠PQR+∠1 = 180° – ∠PSQ
तथा ∠PRQ+∠2 = 180° – ∠PSQ
.: 180° – ∠PSQ > 180°- ∠PSR [(1) से]
⇨ – ∠PSQ > ∠PSR
⇨ ∠PSQ > ∠PSR अर्थात् ∠PSR > ∠PSQ
6. दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने
रेखाखंड खींचे जा सकते हैं उनमें लम्ब सबसे छोटा होता है।
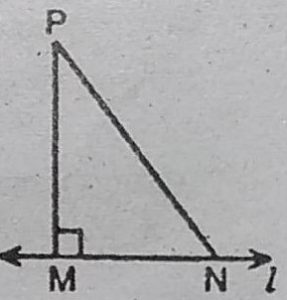
हल : माना कि P कोई बिंदु है, जो कि सीधी रेखा l पर नहीं है
तथा PM ⊥ l, M के अलावा रेखा l पर N कोई बिंदु है।
∆PMN में, ∠M = 90°
⇨ ∠N < 90°
[चूंँकि ∠M = 90° ⇨∠MPN+ ∠PNM = 90°]
⇨∠P + ∠N= 90° ⇨ ∠N < 90°]
⇨ ∠N < ∠M
⇨ PM < PN
[चूँकि बड़े कोण के सम्मुख भुजा बड़ी होती है।]
अत: P से AP तक रेखाखंडों में से PM सबसे छोटा रेखाखंड है।
प्रश्नावली 7.5 (ऐच्छिक)
1. ABC एक त्रिभुज है । इसके अभ्यंतर एक ऐसा बिंदु ज्ञात कीजिए जो ∆ABC के
तीनों शीर्षों से समदूरस्थ है।
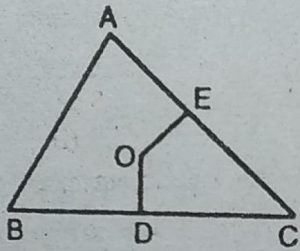
हल : ∆ABC में माना OD तथा OE, क्रमशः भुजा BC
तथा CA के लम्ब समद्विभाजक है।
.: O रेखाखंड BC के दोनों छोरों B तथा C से समान
दूरी पर है। क्योंकि O, BC के लम्ब समद्विभाजक पर
स्थित है। इसी प्रकार O,C तथा A से भी समान दूरी पर है।
इसीलिए, भुजा BC,CA तथा AB के लम्ब समद्विभाजकों का प्रतिच्छेदन बिंदु O, आवश्यक बिंदु है जो ∆ ARC के शीर्षों से समदूरस्थ है।
2. किसी त्रिभुज के अभ्यंतर एक ऐसा बिंदु ज्ञात कीजिए जो त्रिभुज की सभी भुजाओं से समदूरस्थ है।

हल : माना कि BE तथा CF क्रमश: ∠ABC
तथा ∠ACB के कोण समद्विभाजक हैं। ये AC
तथा AB को क्रमश: E तथा F पर काटते हैं।
चूँकि O, ∠ABC के कोण समद्विभाजक BE पर
स्थित है। इसलिए O, AB तथा BC से समान दूरी पर है।
3. एक बड़े पार्क में, लोग तीन बिंदुओं (स्थानों) पर केन्द्रित हैं (देखिए आकृति):
A : जहाँ बच्चों के लिए फिसल पट्टी और
झूले हैं।
B: जिसके पास मानव-निर्मित एक झील है।
C: जो एक बड़े पार्किंग स्थल और बाहर
निकलने के रास्ते के निकट है।
एक आइसक्रीम का स्टॉल कहाँ लगाना चाहिए
ताकि वहाँ लोगों की अधिकतम संख्या पहुँच
सके?
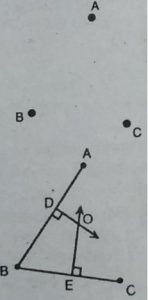
हल : आइसक्रीम का स्टॉल A, B तथा C से
समान दूरी पर होना चाहिए जिसके लिए लम्ब
समद्विभाजकों का प्रतिच्छेदन बिंदु स्थापित करना
पड़ेगा।
इसीलिए O आवश्यक बिंदु है जो कि A, B तथा
C से समान दूरी पर होगा।
4. षडभुजीय और तारे के आकार की रंगोलियों (देखिए आकृति (i) और (ii)] को 1cm भुजा वाले समबाहु त्रिभुजों से भर कर पूरा कीजिए । प्रत्येक स्थिति में, त्रिभुजों की संख्या गिनिए । किसमें अधिक त्रिभुज हैं ?
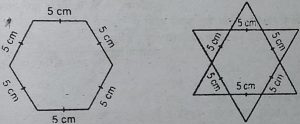
हल : प्रत्येक आकृति को 1 cm के समबाहु
त्रिभुजों के साथ भरने पर हमें प्राप्त हुआ कि
आकृति (i) में इस प्रकार के त्रिभुजों की
संख्या = 150 तथा आकृति (ii) में इस प्रकार
के त्रिभुजों की संख्या 300 है।

●
