BIHAR BOARD CLASS 9TH MATH | रेखाएँ और कोण
BIHAR BOARD CLASS 9TH MATH | रेखाएँ और कोण
Bihar Board Solutions for Class 9 Maths Chapter 6 Lines and Angles (रेखाएँ और कोण)
रेखाएँ और कोण
प्रश्नावली 6.1
1. आकृति में, रेखाएँ ABऔर CD बिंदु O पर प्रतिच्छेद
करती हैं। यदि ∠AOC+∠BOE = 70° है और
∠BOD=40° है, तो ∠BOE और प्रतिवर्ती
∠COE ज्ञात कीजिए।
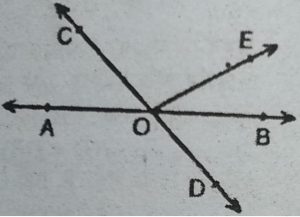
[रैखिक युग्म]
हल : चूँकि OA तथा OB विपरीत किरणें हैं। इसलिए
AB एक रेखा है। चूँकि किरण OC,AB पर आधारित
है। इसलिए,
∠AOC+ZCOB = 180°
⇨ ∠AOC+∠COE+ ∠BOE = 180° [चूँकि∠COB = ∠COE+∠BOE]
⇨ (∠AOC+∠BOE)+∠COE = 180°
⇨ 70°+ZCOE = 180° [ चूँकि AOC + ZBOE = 70° (दिया है।]
⇨ ∠COE= 180°-70°=110°
.: प्रतिवर्ती ∠COE = 360°-110° = 250°
चूँकि OC तथा OD विपरीत किरणें हैं इसलिए
∠COE+∠EOD= 180° [रैखिक युग्म]
⇨ ∠COE+∠BOE+ ∠BOD= 180°
⇨ 110°+∠BOE+40°= 180°
[चूँकि∠COE = 110° (ऊपर सिद्ध किया गया है), ∠BOD = 40° (दिया है)]
⇨ ∠BOE= 180°-110°-40°= 30°
अत: ∠BOE = 30° तथा प्रतिवर्ती ∠COE = 250°
2. आकृति में, रेखाएँ XY और MN बिंदु O पर
प्रतिच्छेद करती हैं। यदि ∠POY = 90° और
a:b=2:3 है, तो c ज्ञात कीजिए।

हल : चूँकि a: b = 2:3 तथा a+b = ∠POX =
∠POY = 90° तथा अनुपातों का योग 2 + 3 = 5
.: a=2/5×90° = 2×18° = 36° तथा
b= 3/5×90°=3×18°= 54°
चूँकि OM और ON विपरीत किरणें हैं। इसलिए MN एक रेखा है।
चूँकि किरण OX, MN पर स्थित है, इसलिए
∠MOX+ ∠XON = 180° [ रैखिक युग्म]
⇨ c+ b = 180° ⇨ c+54° = 180°
⇨ c= 180°-54° = 126°
अत: c=126°
3. आकृति में, यदि ∠PQR = ∠PRQ है, तो सिद्ध
कीजिए कि ∠PQS = ∠PRT है।
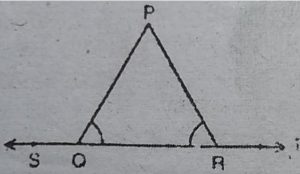
हल : चूँकि QS और QR विपरीत किरणें हैं, इसलिए
SR एक रेखा है चूँकि QP, SR पर स्थित है।
.: ∠PQS+∠PQR = 180° रैखिक युग्म …(1)
पुन: RQ और RT विपरीत किरणें हैं। इसलिए QT एक रेखा है ।
चूँकि PR, QT पर स्थित है।
.: ∠PRQ+ ∠PRT = 180° रैखिक युग्म …(2)
(1) तथा (2) से
∠PQR + ∠PQR=∠PRQ+ ∠PTR [चूँकि प्रत्येक भुजा = 180°] ….(3)
तथा ∠PQR = ∠PRQ [दिया है| ….(4)
(4) को (3) में से घटाने पर ∠PQS = ∠PRT.
4. आकृति में, यदि x+y = w+z है, तो सिद्ध कीजिए कि AOB एक रेखा है।
हल : चूँकि एक बिन्दु के चारों ओर के कोणों का योग 360° होता है।
.: (∠BOC+∠COA) + (∠BOD+ ∠AOD) = 360°
(x+y) + (w+z)= 360°
लेकिन x+y = w+z [दिया है।
x+y=w+z =360°/2 = 180°
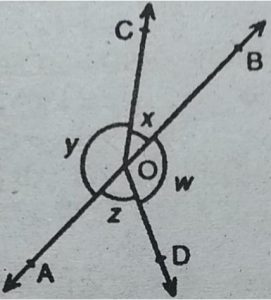
इसलिए ∠BOC तथा ∠COA, ∠BOD तथा ∠AOD
रैखिक युग्म बनाते हैं। परिणामस्वरूप OA और OB
दो विपरीत किरणें हैं। इसलिए AOB एक सीधी रेखा
है।
5. आकृति में, POQ एक रेखा है। किरण OR रेखा
PQ पर लम्ब है। किरणों OPऔर OR के बीच में
OS एक अन्य किरण है। सिद्ध कीजिए :
∠ROS = 1/2(∠QOS – ∠POS)
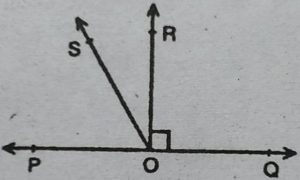
हल : चूँकि OR रेखा PQ पर लम्ब है।
.: ∠POR= ∠ROQ [ चूँकि प्रत्येक = 90°]
⇨ ∠POS + ∠ROS = ∠QOS = – ∠ROS
⇨ 2∠ROS = ∠QOS – ∠POS
⇨ ∠ROS=1/2( ∠QOS-∠POS)
6. यह दिया है कि ∠XYZ = 64° है और XY को बिंदु P तक बढ़ाया गया है। दी हुई
सूचना से यह एक आकृति खींचिए। यदि किरण YQ, ∠ZYP को समद्विभाजित
करती है, तो ∠XYQ और प्रतिवर्ती ∠QYP का मान ज्ञात कीजिए।
हल : चूँकि XY को बिन्दु P तक बढ़ाया। इसलिए XP एक सीधी रेखा है।
चूँकि YZ,XP पर स्थित होती है।
.: ∠XYZ+∠ZYP= 180° [रैखिक युग्म]
⇨ 64°+∠ZYP= 180° [चूँकि 2XYZ = 64°]
⇨ ∠ZYP=180°-64°=116°
चूँकि किरण YQ, ∠ZYP को समद्विभाजित करती है।
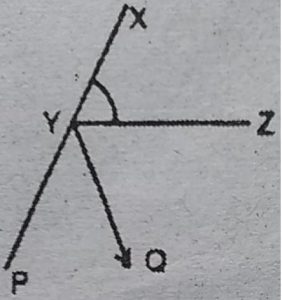
इसलिए ∠QYP= ∠ZYQ = 116°/2 = 58°
अब ∠XYQ = ∠XYZ + ∠ZYQ
⇨ ∠XYQ= 64°+58° = 122°
तथा प्रतिवर्ती ∠QYP = 360° – ∠QYP = 360° – 58° = 302°
प्रश्नावली 6.2
1. आकृति में, x और y के मान ज्ञात कीजिए और
फिर दर्शाइए कि AB || CD है।
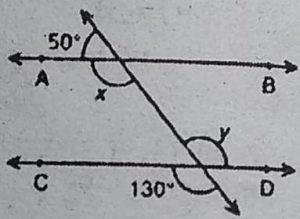
हल : चूँकि AB ∥ CD तथा तिर्यक रेखा PQ
उनको क्रमशः R तथा S पर काटती है।
.: ∠ARS = ∠RSD [एकान्तर कोण]
⇨ x=y
लेकिन ∠RSD = ∠CSQ [शीर्षाभिमुख कोण]
⇨ y= 130° [चूंकि ∠CSQ=130°]
अतः x= y= 130
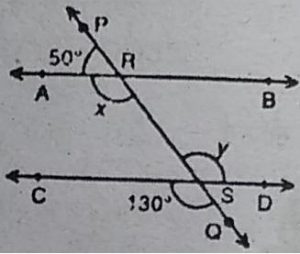
2 आकृति में, यदि AB || CD, CD || EF और
y:z=3:7 है, तो x का मान ज्ञात कीजिए।
हल : चूंकि CD∥EF तथा तिर्यक रेखा PQ उनको
क्रमशः S तथा T पर काटती है।
.: ∠CST = ∠STF [एकान्तर कोण]
⇨ 180°-y=z [ चूँकि ∠y+ ∠CST = 180° रैखिक युग्म]
⇨ y+2= 180°
दिया है y:z=3:7, अतः
अनुपातों का योग =3+7= 10 है।
.: y = 3/10 x180° =3×18° = 54°
तथा z=7/10×180° =7×18° = 126°
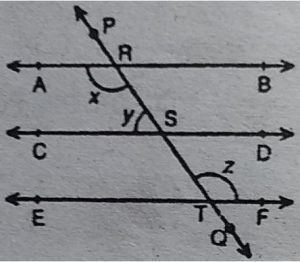
चूँकि AB ∥ CD तथा तिर्यक रेखा PQ उनको
क्रमश: R तथा S पर काटती है।
.: ∠ARS + ∠RSC = 180° [लगातार अभ्यंतर कोण सम्पूरक होते हैं]
⇨ x+y =180°
⇨ x= 180° -y= 180° -54° = 126° [चूँकि y=54°]
अतः x =126°
3. आकृति में, यदि AB || CD, EF⊥CD और ∠GED = 126° है, तो ∠AGE, ∠GEF
और ∠FGE ज्ञात कीजिए।
हल : चूँकि AB || CD तथा तिर्यक रेखा GE
उनको क्रमश: G तथा E पर काटती है।
.: ∠AGE = ∠GED
[एकान्तर कोण]
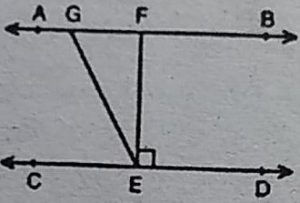
⇨ ∠AGE = 126° [चूँकि ∠GED = 126° (दिया है)]
∠GEF = ∠GED-∠FED = 126°-90° =36°
तथा ∠FGE =∠GEC [एकान्तर कोण]
⇨ ∠FGE = 90° -∠GEF= 90°-36° = 54°
अत: ∠AGE = 126°, ∠GEF=36°
और ∠FGE = 54°
4. आकृति में, यदि PQ ||ST, ∠PQR= 110° और ∠RST = 130° है, तो ∠QRS ज्ञात
कीजिए।
हल : PQ को M बिन्दु पर काटने के लिए SR
तक बढ़ाया।
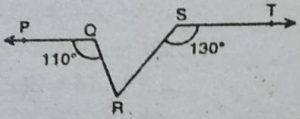
अब PM || ST तथा तिर्यक रेखा SM क्रमशः
उनको M तथा R पर काटती है।
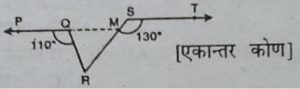
∠SMQ = ∠TSM [एकान्तर कोण]
∠SMQ = 130°
∠QMR = 180° – 130° = 50° [ चूँकि ∠SMQ + ∠QMR= 180° (एकांतर युग्म)
चूँकि किरण RQ, PM को Q पर काटती है।
.: ∠PQR + ∠RQM = 180°
⇨ 110° +∠RQM = 180° =∠RQM = 70°
.: ∠QRS = 180° -(70° + 50°) = 60°
[चूँकि एक त्रिभुज के तीनों कोणों का योग 180° होता है।
5. आकृति में, यदि AB || CD,∠APQ = 50° और
∠PRD = 127° है, तो x और y ज्ञात कीजिए।
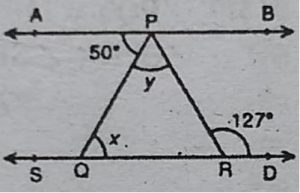
हल: चूँकि AB || CD तथा तिर्यक रेखा PQ उनको
क्रमशः P और Q पर काटती है।
.: ∠PQR =∠APQ [एकान्तर कोण]
⇨ x =50° [चूँकि ∠APQ = 50° (दिया है)]
चूँकि AB || CD तथा तिर्यक रेखा PR उनको क्रमशः P तथा R पर काटती है।
.: ∠APR = ∠PRD [एकान्तर कोण]
⇨ ∠APQ + ∠QPR = 127° [चूँकि ∠PRD = 127°]
⇨ 50° + y = 127° [चूँकि ∠APQ= 50°]
⇨ y= 127°-50° = 77°
अत: x=50° तथा y= 77°
6. आकृति में, PQ और RS दो दर्पण हैं जो एक दूसरे के समांतर रखे गए हैं। एक
आपतन किरण (incident ray) AB, दर्पण PQ से B पर टकराती है और परावर्तित
किरण (reflected ray) पथ BC पर चलकर दर्पण RS से C पर टकराती है तथा पुनः
CD के अनुदिश परावर्तित हो जाती है। सिद्ध कीजिए कि AB || CD है।
हल : दो समतल दर्पण PQ तथा RS एक-दूसरे के
समांतर स्थित हैं।
अर्थात् PQ || RS
एक आपतित किरण AB परावर्तित होने के बाद रास्ता
BC और CD से होकर जाती है।
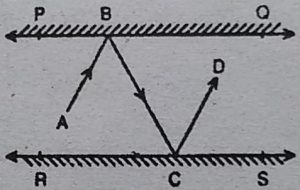
BN तथा CM क्रमशः समतल दर्पण PQ तथा
RS के अभिलम्ब हैं।
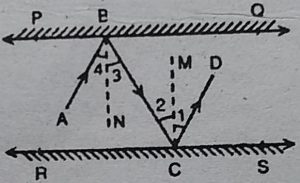
चूंकि BN⊥PQ,CM⊥RS तथा PQ|| RS
.: BN⊥RS⇨ BN ∥ CM
इसलिए BN तथा CM दो समांतर रेखाएँ हैं तथा
तिर्यक रेखा BC उनको क्रमश: B तथा C पर
काटती है।
.: ∠2 = ∠3 [एकान्तर अन्त:कोण]
लेकिन, ∠1 = ∠2 और ∠3 = ∠4 [परावर्तन के नियम के अनुसार]
.: ∠1 + ∠2 = ∠2+ ∠2
और ∠3 + ∠4 = ∠3 + ∠3
⇨ ∠1 + ∠2 = 2 (∠2)
और ∠3 + ∠4 = 2(∠3)
⇨ ∠1 + ∠2 = ∠3 + ∠4 [ चूँकि ∠2 = ∠3 = 2(∠2) = 2 (∠3)]
⇨ ∠ABC = ∠BCD
इसलिए रेखा AB और CD तिर्यक रेखा BC द्वारा इस प्रकार काटी जाती है कि
∠ABC = ∠BCD
अर्थात् एकान्तर अन्तः कोण बराबर होते हैं।
इसलिए AB || CD
प्रश्नावली 6.3
1. आकृति में, ∆PQR की भुजाओं QP और RQ को क्रमशः
बिंदुओं S तथा T तक बढ़ाया गया है। यदि ∠SPR= 135°
है और ∠PQT = 110° है, तो ∠PRQ ज्ञात कीजिए।
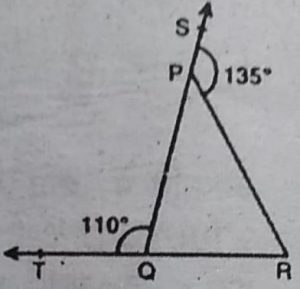
हल : ∠QPR + ∠SPR = 180° [रैखिक युग्म]
⇨ ∠QPR + 135° = 130°
⇨ ∠QPR = 180° -135° = 45°
अब ∠TQP = ∠QPR + ∠PRQ [बाह्य कोण प्रमेय से)
⇨ 110° = 45° + ∠PRQ
⇨ ∠PRQ = 110°-45° 3D65°
अतः ∠PRQ = 65°
2. आकृति में, ∠x = 62° और ∠XYZ=54° है। यदि YO
और ZO क्रमश: ∆XYZ के ∠XYZ और ∠XZY के
समद्विभाजक हैं, तो ∠OZY और ∠YOZ ज्ञात कीजिए।
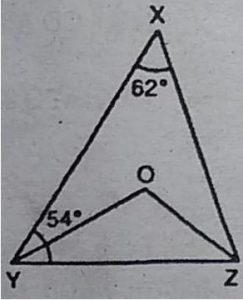
हल : ∆XYZ को लेने पर
∠YXZ+ ∠XYZ+ ∠XZY = 180°
[कोणों के योग का गुण)
⇨ 62° +54° + ∠XZY = 180° [चूँकि ∠YXZ = 62°, ∠XYZ = 54°]
⇨ ∠XZY= 180°-62°-54° = 64°
चूँकि YO तथा ZO, ∠XYZ तथा ∠XZY के कोण समद्विभाजक हैं, इसलिए
∠OYZ = 1/2×∠XYZ = 1/2×54°=27°
तथा ∠OZY = 1/2 ∠XZY=1/2×64°=32°
∆OYZ में,
∠YOZ+ ZOYZ+ ∠OZY = 180° [कोणों के योग का गुण]
⇨ ∠YOZ+27° + 32° = 180°
⇨ ∠YOZ = 180° – 27°-32° = 121°
अत: ∠OZY = 32° तथा ∠YOZ = 121°
3. आकृति में, यदि AB || DE,∠BAC = 35°
और ∠CDE = 53° है, तो ∠DCE ज्ञात
कीजिए।

हल: चूंकि AB || DE तथा तिर्यक रेखा AE
उनको क्रमशः A तथा E पर काटती है।
.: ∠DEA = ∠BAE [एकान्तर कोण]
⇨ ∠DEC=35° [चूँकि ZDEA तथा ZDEC = 35°]
∆ DEC में,
∠DCE+ ∠DEC+ ∠CDE = 180° [कोणों के योग का गुण]
⇨ ∠DCE+35° +53° = 180°
⇨ ∠DCE=180°-35°-53°=92°
अत: ∠DCE=92°
4. आकृति में, यदि रेखाएँ PQ और RS बिन्दु T पर
इस प्रकार प्रतिच्छेद करती हैं कि ∠PRT = 40°,
∠RPT = 95° और ∠TSQ = 75° है, तो ∠SQT
ज्ञात कीजिए।
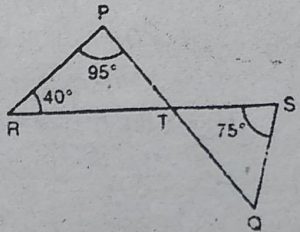
हल : ∆ PRT में,
∠PRT + ∠RTP+ ∠TPR = 180° [कोणों के योग का गुण]
⇨ 40°+∠RTP +95° =180°
⇨ ∠RTP =180° – 40°- 95°= 45° ∠STQ =∠RTP [शीर्षाभिमुख कोण]
⇨ ∠STQ=45° [चूँकि ∠RTP = 45° (सिद्ध हुआ)]
∆TQS में,
∠SQT+∠STQ+∠TSQ=180° [कोणों के योग का गुण)
⇨ ∠SQT + 45°+75°=180° [चूँकि STQ = 45° (सिद्ध हुआ)
अत: ∠SQT=60°
5. आकृति में, यदि PQ⊥PS, PQ∥SR, ∠SQR = 28° और ∠QRT = 65° है, तो xऔर y का मान ज्ञात कीजिए।
हल : ∆SRQ में बाह्य कोण गुण का उपयोग करते
∠QRT = ∠RQS + ∠QSR
⇨ 65° =28° + 2QSR
[चूँकि ∠QRT = 65°, ∠RQS = 28°]
⇨ ∠QSR = 65°-28° = 37°
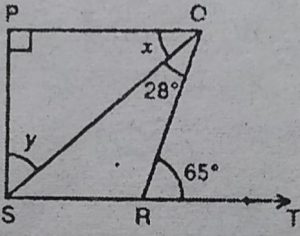
चूँकि PQ|| SR तथा तिर्यक रेखा PS उनको क्रमश: P तथा S पर काटती है।
.: ∠PSR+ ∠SPQ = 180° [चूँकि त्रिभुज के अन्तः कोणों का योग 180°]
⇨ (∠PSQ+ ZQSR)+ 90° = 180°
⇨ y+37°+90° = 180°
⇨ y=180°-90°-37° =53°
समकोण ∆ SPQ में, ∠PQS + ∠PSQ = 90°
⇨ x + 53° =90°
⇨ x= 90° – 53°=37°
अतः x=37° तथा y=53°
6. आकृति में, ∆ PQR की भुजा QR को बिंदु
तक बढ़ाया गया है। यदि ∠PQR और ∠PRS
के समद्विभाजक बिंदु T पर मिलते हैं, तो सिद्ध
कीजिए कि ∠QTR=1/2∠QPR है।

हल : ∆ PQR में, बाह्य ∠PRS = ∠P + ∠Q
⇨ 1/2 बाह्य ∠PRS = 1/2 ∠P+1/2 ∠Q
⇨ ∠TRS =1/2 ∠P+∠TQR …..(1)
[चूंँकि QT तथा RT क्रमश: ∠Q तथा ∠PRS के कोण समद्विभाजक हैं।]
.: ∠Q = 2∠TQR तथा बाह्य ∠PRS = 2 ∠TRS
∆QRT में, बाह्य ∠TRS = ∠TQR + ∠T ……(2)
(1) तथा (2) से, 1/2 ∠P+ ∠TQR = ∠TQR + ∠T 1/2 ∠P = ∠T
⇨ ∠QTR = 1/2 ∠QPR
●
