BIHAR BOARD CLASS 9TH MATH | वृत्त
BIHAR BOARD CLASS 9TH MATH | वृत्त
Bihar Board Solutions for Class 9 Maths Chapter 10 Circle (वृत्त)
वृत्त
प्रश्नावली 10.1
1. खाली स्थान भरिए:
(i) वृत्त का केन्द्र वृत्त के …………में स्थित है (बहिर्भाग/अभ्यंतर)।
(ii) एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के……..में
स्थित होता है (बहिर्भाग/अभ्यंतर)।
(iii) वृत्त की सबसे बड़ी जीवा वृत्त का ……….होता है।
(iv) एक चाप ………. होता है, जब इसके सिरे एक व्यास के सिरे हों।
(v) वृत्तखंड एक चाप तथा …….. के बीच का भाग होता है।
(vi) एक वृत्त, जिस तल पर स्थित है, उसे ……. भागों में विभाजित करता है।
हल : (i) अभ्यंतर (ii) बहिर्भाग (iii) व्यास (iv) अर्ध गोला (v) एक जीवा (vi) तीन ।
2. लिखिए, सत्य या असत्य । अपने उत्तर के कारण दीजिए।
(i) केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखंड वृत्त की त्रिज्या होती है।
(ii) एक वृत्त में समान लंबाई की परिमित जीवाएँ होती हैं।
(iii) यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भाग दीर्घ चाप
होता है।
(iv) वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दो गुनी हो, वृत्त का व्यास है।
(v) त्रिज्यखंड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
(vi) वृत्त एक समतल आकृति है।
हल : (i) सत्य : क्योंकि त्रिज्या को दो तरीके से उपयोग किया जाता है-एक रेखाखंड
के रूप में तथा एक लंबाई के रूप में।
(ii) असत्य : क्योंकि वृत्त पर अनन्त बिन्दु स्थित होते हैं। अतः हम अनन्त जीवाएँ किन्हीं
भी दो बिन्दुओं को मिलाने पर प्राप्त करते हैं।
(iii) असत्य : चूँकि ये चाप लम्बाई में बराबर हैं इसलिए ये बराबर चाप कहलाती हैं।
(iv) सत्य : क्योंकि व्यास सबसे बड़ी जीवा होती है तथा इसकी लंबाई वृत्त की त्रिज्या
से दोगुनी होती है।
(v) असत्य : क्योंकि चाप तथा दो त्रिज्याओं के बीच का क्षेत्र, केन्द्र को चाप के अन्तः
बिन्दु से मिलाने वाला त्रिज्यखंड कहलाता है। ।
(vi) सत्य : क्योंकि वृत्त एक बिन्दु का बिन्दुपथ होता है जो एक तल में इस प्रकार घूमे
कि एक तल में स्थिर बिन्दु से उसकी दूरी नियत रहे । इसलिए वृत्त एक तल में स्थित
है।
प्रश्नावली 10.2
1. याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों, सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
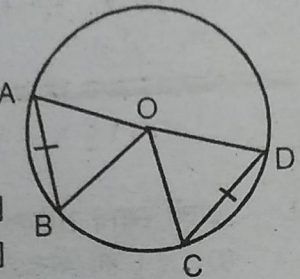
हल : दिया है : AB तथा CD,O केन्द्र
वाले वृत्त की दो बराबर जीवाएँ हैं।
सिद्ध करना है: ∠AOB = ∠COD.
उपपत्ति: ∆AOB तथा ∆COD में,
AO = CO [एक ही वृत्त की क्रियाएँ।]
BO = DO [एक ही वृत्त की क्रियाएँ।]
तथा, AB = CD [दिया है।]
.: SSS सर्वांगसम गुणधर्म से
∆AOB≈∆COD
⇨ ∠AOB =∠COD [सर्वांगसम त्रिभुजों के संगत भाग]
2. सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करें, तो जीवाएं बराबर होती हैं।
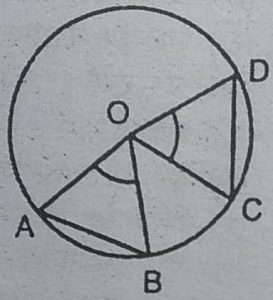
हल : दिया है : AB तथा CD दो इस प्रकार को जीवाएँ हैं कि इसके द्वारा वृत्त के केन्द्र पर अंतरित कोण बराबर है।
अर्थात् ∠AOB = ∠COD
सिद्ध करना है: AB = CD
उपपत्ति: ∆AOB तथा ∆COD में,
AO = CO
[एक ही वृत्त की त्रिज्याएँ।]
BO = DO
[एक ही वृत्त की त्रिज्याएँ]
तथा ∠AOB = ∠COD
.: SAS सर्वांगसमता गुणधर्म से,
∆AOB≈ ∆COD
⇨ AB = CD [सर्वांगसम त्रिभुजों के संगत भाग]
प्रश्नावली 10.3
1. वृत्तों के कई जोड़े (युग्म) खींचिए । प्रत्येक जोड़े में कितने बिन्दु उभयनिष्ठ हैं ? उभयनिष्ठ बिन्दुओं की अधिकतम संख्या क्या है?
हल : वृत्त के विभिन्न जोड़े खींचने पर, हम पाते हैं कि उनके दो उभयनिष्ठ बिन्दु हैं। अब हम यह सिद्ध करेंगे कि वृत्तों के जोड़े एक-दूसरे को दो से अधिक बिन्दुओं पर प्रतिच्छेद नहीं कर सकते।
माना कि दो वृत्त एक-दूसरे को तीन बिन्दुओं पर काटते हैं। लेकिन तीन बिन्दुओं से केवल एक ही वृत्त गुजर सकता है। अतः यदि वृत्त एक-दूसरे को प्रतिच्छेद करते हैं तो वे केवल दो बिन्दुओं पर प्रतिच्छेद करते हैं। ये दोनों बिन्दु उनकी उभयनिष्ठ जीवा के अन्त: बिन्दु होते हैं। यह जीवा, उन सभी वृत्तों की उभयनिष्ठ जीवा हो सकती है जो कि इस उभयनिष्ठ जीवा के अन्तः बिन्दुओं से होकर गुजरते हैं।
2. मान लीजिए आपको एक वृत्त दिया है। एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।
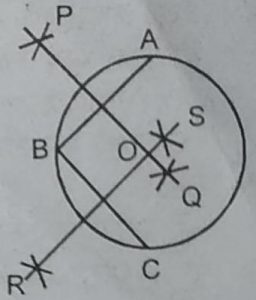
हल : रचना के पद :
1. तीन बिन्दु A, B तथा C (वृत्त की परिधि पर) लें।
2. AB तथा BC को मिलाएँ।
3. AB तथा BC के लम्ब समद्विभाजक PQ तथा
PS खींचे जो कि एक-दूसरे को O पर प्रतिच्छेद
करते हैं। तब, O वृत्त का केन्द्र है।
3. यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब समद्विभाजक पर स्थित हैं।
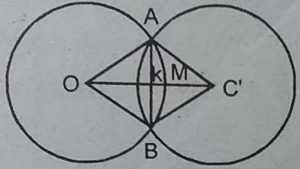
हल : दिया है : दो वृत्त जिनके केन्द्र O तथा O’
हैं। दो बिन्दुओं A तथा B पर इस प्रकार प्रतिच्छेद
करते हैं कि AB दोनों वृत्तों की उभयनिष्ठ जीवा
है तथा OO’ एक रेखाखंड है जो कि वृत्तों के
केन्द्र को मिलाती है।
माना कि OO’, AB को M पर प्रतिच्छेद करती है।
सिद्ध करना है: OO’ AB का लम्ब समद्विभाजक है।
रचना : रेखाखंड OA, OB, O’A तथा O’B खींचें।
उपपत्ति: ∆OAO’ तथा ∆OBO’ में,
OA = OB [एक ही वृत्त की त्रिज्याएँ।]
O’A = O’B [एक ही वृत्त की त्रिज्याएँ।]
तथा, OO’ = OO’ [उभयनिष्ठ]
SSS सर्वांगसमता गुणधर्म से,
∆OAO’ ≈ ∆OBO’
⇨ ∠AOO’ = ∠BOO’
⇨ ∠AOM = ∠BOM ….(1)
[चूँकि∠AOO’ = ∠AOM तथा ∠BOM = ∠BOO’]
∆AOM तथा ∆BOM में,
OA = OB [एक वृत्त की त्रिज्या]
∠AOM = ∠BOM [उभयनिष्ठ]
तथा OM = OM [समीकरण 1 से]
.: सर्वांगसम गुणधर्म SAS से,
∆AOM = ∆BOM
⇨ AM = BM तथा ∠AMO =∠BMO
लेकिन ∠AMO + ∠BMO = 180°
.: 2∠AMO = 180°
⇨ ∠AMO = 90°
इसलिए AM = BM तथा ∠AMO = ∠BMO = 90°
अत: OO’AB का लम्ब समद्विभाजक है।
प्रश्नावली 10.4
1. 5 cm तथा 3cm त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके
केन्द्रों के बीच की दूरी 4 cm है । उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
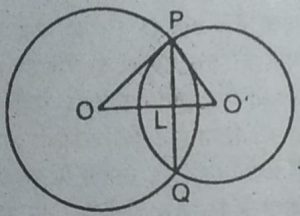
हल : माना O तथा O’ क्रमशः 5 cm तथा 3 cm त्रिज्याओं वाले वृत्तों के केन्द्र हैं तथा
PQ उनकी उभयनिष्ठ जीवा है जिसमें OP = 5 cm, O’P = 3 cm तथा OO’ = 4 cm हैं।
चूँकि OP² = PO’²+O’O² [चूँकि 5² = 3² + 4²]
OO’P एक समकोण त्रिभुज है।
∆OO’P का क्षेत्रफल = 1/2×O’P×OO’
=1/2×3×4
=6 वर्ग मात्रक ….(1)
तथा क्षेत्रफल ∆OO’P = 1/2×OO’×PL
=1/2×4× PL = 2PL …..(2)
समी. (1) तथा (2) को जोड़ने पर,
2× PL=6 ⇨ PL=3
हम जानते हैं कि जब दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तब उनका केन्द्र उनकी
उभयनिष्ठ जीवा का लम्ब समद्विभाजक होता है। अर्थात् 00′ रेखा PQ का लम्ब
समद्विभाजक है।
PQ = 2× PL= (2×3) cm =6cm
2. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए
कि एक जीवा के दोनों खंड दूसरी जीवा के संगत खंडों के बराबर हैं।
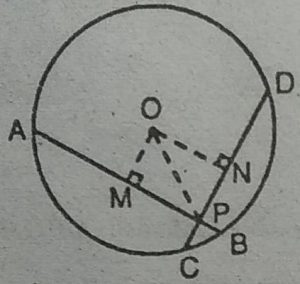
हल : दिया है : AB तथा CD वृत्त की जीवाएँ हैं,O
वृत्त का केन्द्र है। AB तथा CD,P पर प्रतिच्छेद करते
हैं और AB = CD ।
सिद्ध करना है : (i) AP = PD (ii) PB = CP
रचना : OM ⊥AB, ON⊥CD खींचें।
OP को मिलाया
प्रमाण: AM = MB = 1/2 [केन्द्र से खींचा गया लम्बा जीवा
को समद्विभाजित करता है।]
CN = ND = 1/2 CD केन्द्र से खींचा गया लम्ब जीवा को
समद्विभाजित करता है।]
AM = ND तथा MB = CN …..(1)
[चूँकि AB = CD (दिया है)]
∆OMP तथा ∆ONP में,
OM = ON [एक वृत्त की समान जीवाएँ केन्द्र से
एक समान दूरी पर स्थित होती हैं।]
∠OMP = ∠ONP [ प्रत्येक = 90°]
OP = OP [उभयनिष्ठ]
सर्वांगसम गुणधर्म RHS से,
Δ ΟΜΡ ≈ ΔΟΝΡ
⇨ MP = PN …..(2) [सर्वांगसम त्रिभुजों के संगत भाग]
समी. (1) तथा (2) को जोड़ने पर,
AM + MP = ND + PN ⇨ AP = PD
समी. (1) में से समी. (2) को घटाने पर,
MP-MP = CN-PN PB ⇨ PB=CP
अत: (i) AP = PD और (ii) PB = CP.
3. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अदर प्रतिच्छेद करें, तो सिद्ध कीजिए कि
प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
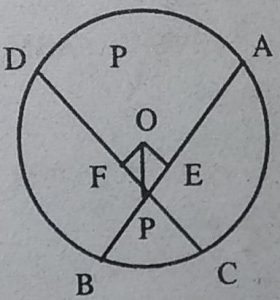
हल : दिया है : AB तथा CD वृत्त की जीवाएँ हैं, O वृत्त का केन्द्र है। AB तथा CD,
P पर प्रतिच्छेद करते हैं तथा AB = CD I
सिद्ध करना है: ∠OPE = ∠OPF
रचना : OE ⊥AB तथा OF ⊥CD खींचें OP को मिलाया।
प्रमाण : ΔOEP तथा ΔOFP में,
∠OEP = ∠OFP [चूँकि प्रत्येक = 90°]
OP = OP [उभयनिष्ठ]
OE = OF [एक वृत्त की समान
जीवाएँ केन्द्र से समान दूरी पर स्थित होती हैं।]
.: समकोण कर्ण भुजा सर्वांगसमता गुणधर्म से
ΔOEP ≈ΔOFP
⇨ ∠OPE = ∠OPF [सर्वांगसम त्रिभुजों के संगत भाग]
4. यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र
वाले वृत्त) को, जिनका केन्द्र O है, A,B,C
और D पर प्रतिच्छेद करें, तो सिद्ध कीजिए AB
= CD है ( देखिए आकृति)।
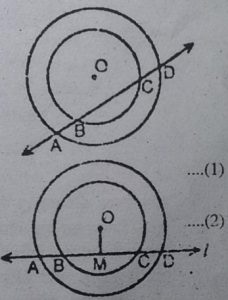
हल : माना कि O से OM रेखा l पर लम्ब है।
हम जानते हैं कि केन्द्र से जीवा पर खींचा गया लम्ब,
जीवा को समद्विभाजित करता है।
चूँकि BC छोटे वृत्त की जीवा है तथा OM⊥BC
.: BM = CM …. (1)
पुनः, AD बड़े वृत्त की जीवा है तथा OM ⊥ AD
.: AM = DM …..(2)
समी. (2) में से (1) को घटाने पर,
AM- BM = DM-CM
⇨ AB = CD
5. एक पार्क में बने 5m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं
मनदीप खेल रही हैं । रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा
मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा
मनदीप के बीच की प्रत्येक दूरी 6m हो, तो रेशमा और मनदीप के बीच की दूरी क्या
है?
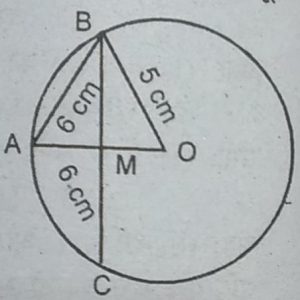
हल : माना कि तीनों लड़कियाँ रेशमा, सलमा और
मनदीप क्रमश: 5 cm की त्रिज्या वाले वृत्त पर बिन्दु
B,A तथा C पर खड़ी हैं।
हम जानते हैं कि AB तथा AC एक वृत्त की दो
समान जीवाएँ हैं तब वृत्त का केन्द्र ∠BAC के
समद्विभाजक पर स्थित होगा।
यहाँ AB =AC=6 cm. इसलिए ∠BAC का समद्विभाजक केन्द्र O से होकर गुजरता
है। अर्थात्, OA ∠BAC का समद्विभाजक है।
चूँकि कोण का आंतरिक कोण समद्विभाजक सम्मुख रेखा को कोण बनाने वाली रेखाओं
के अनुपात में बाँटता है।
.: M,BC को 6:6=1:1 के अनुपात में बाँटता है अर्थात् M, BC का मध्य बिन्दु है।
⇨ OM ⊥ BC
समकोण ∆ABM में, AB² = AM² + BM²
⇨ 36 = AM²+ BM²
⇨ BM² = 36-AM² ….(1)
समकोण ∆OEM में, OB²= OM² + BM²
⇨ 25 = (OA-AM)² + BM²
⇨ BM² = 25-(OA – AM)² ….(2)
⇨ BM² = 25-(5-AM)²
समी. (1) तथा (2) से,
36- AM² = 25-(5-AM)²
⇨ 11-AM² + (5-AM)² = 0
⇨ 11-AM² + 25-10AM + AM² = 0
⇨ 10AM – 36 ⇨ AM =3.6
समी. (1) में AM = 3.6 रखने पर,
BM² = 36-(3.6)² = 36-12.96
⇨ BM = √36 – √12.96 = √123.04 = 4.8 cm
⇨ BC = 2BM = 2×4.8 =9.6 cm
अतः रेशमा और मनदीप के बीच की दूरी = 9.6 cm
6. 20m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है। तीन लड़के
अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के
हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है । प्रत्येक फोन की डोरी
की लम्बाई ज्ञात कीजिए।
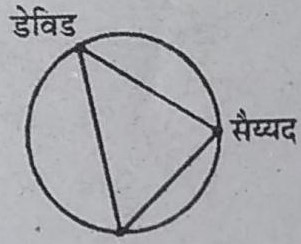
हल : माना कि ABC एक 2xm की भुजा का समबाहु त्रिभुज है।
स्पष्ट रूप से BM = BC/2 =2x/2=xm
समकोण ∆ABM में,
AM² = AB² – BM² = (2x)² -x²=4x² – x²=3x²
⇨ AM = √3x
अब OM = AM-OA = (√3x-20)m
समकोण ∆OBM में,
OB² = BM² + OM²
⇨ 20² = x²+(√3-20)²
⇨ 400 = x² +3x²-40√3x+400
⇨ 4x² – 40√3x=0
⇨ 4x (x -10√3) = 0
चूंकि x≠0,
.: x-10√3 = 0
⇨ x = 10√3
अब BC = 2BM = 2x = 20√3
अतः प्रत्येक फोन की डोरी की लम्बाई = 20-5m
प्रश्नावली 10.5
1. आकृति में, केन्द्र O वाले एक वृत्त पर तीन बिन्दु
A, B और C इस प्रकार है कि ∠BOC = 30°
तथा ∠AOB = 60° है। यदि चाप ABC के
अतिरिक्त वृत्त पर D एक बिन्दु है, तो ∠ADC
ज्ञात कीजिए।
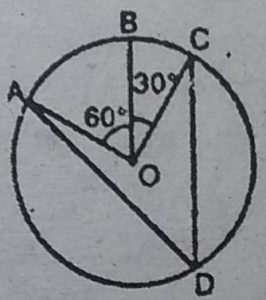
हल : चूँकि एक वृत्त के केन्द्र पर चाप ABC
∠AOC = ∠AOB+ ∠AOC = 60° + 30° = 90°
तथा ∠ADC वृत्त के बचे हुए भाग के एक बिन्दु
पर बनाती है।
.: ∠ADC = 1/2(∠AOC)=1/2×90° = 45°
2. किसी वृत्त की एक जीवा वृत्ते की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी
बिन्दु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिन्दु पर भी अतंरित
कोण ज्ञात कीजिए।
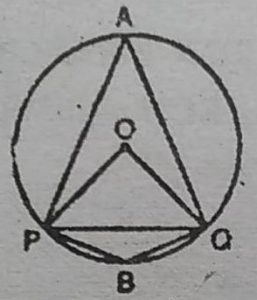
हल : माना PQ एक जीवा है। OP तथा OQ को
मिलाया।
दिया है : PQ = OP=OQ (चूँकि जीवा =त्रिज्या)
.: ∆OPQ एक समबाहु त्रिभुज है।
⇨ ∠POQ=60°
चूँकि चाप PBQ वृत्त के केन्द पर परावर्तन ∠POQ
=360°-60° = 300° बनाती है तथा ∠PBQ वृत्त के
लघु चाप पर बनाती है।
.: ∠PBC = 1/2 (परावर्तन ∠POQ) =1/2×300°=150°
इसी प्रकार, ∠PAB = 1/2(∠POQ)=1/2(60°)=30°
अतः जीवा द्वारा लघु चाप पर बनाया गया कोण 150° तथा दीर्घ चाप पर बनाया गया
कोण = 30°.
3. आकृति में, ∠PQR= 100° है । P, Q तथा R, केन्द्र O वाले एक वृत्त पर स्थित बिन्दु
हैं। ∠OPR ज्ञात कीजिए।
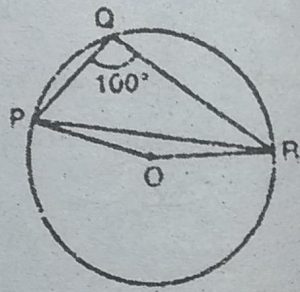
हल : चूँकि एक चाप द्वारा केन्द्र पर बनाया गया
कोण, उसी चाप द्वारा बनाई गई परिधि के बिन्दु पर
कोण का दुगना होता है।
.: परावर्तन ∠POR =2∠PQR
परावर्तन ∠POR = 2×100° = 200°
⇨ ∠POR = 360°-200° = 160°
∆OPR में, OP = OR [एक वृत्त की त्रिज्याएँ।]
⇨ ∠OPR= ∠ORP
[बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।]
तथा ∠POR = 160° [ऊपर सिद्ध किया गया है]
.: ∠OPR =∠ORP = 1/2 (180° – 160°) = 1/2×20°= 10°
अत: ∠OPR = 10°
4. आकृति में, ∠ABC = 69°और ∠ACB = 31°
हो, तो ∠BDC ज्ञात कीजिए।

हल : ∆ABC में,
∠BAC+∠ABC+ ∠BCA = 180°
⇨ ∠BAC+69° +31° = 180°
⇨ ∠BAC = 180° -(69° + 31°)= 180° -100° = 80°
चूँकि एक ही वृत्तखंड में कोण बराबर होते हैं।
.: ∠BDC=∠BAC= 80°
5. आकृति में, एक वृत्त पर A,B, C और D चार
बिन्दु हैं। AC और BD एक बिन्दुE पर इस
प्रकार प्रतिच्छेद करते हैं कि ∠BEC= 130° तथा
∠ECD = 20° है। ∠BAC ज्ञात कीजिए।
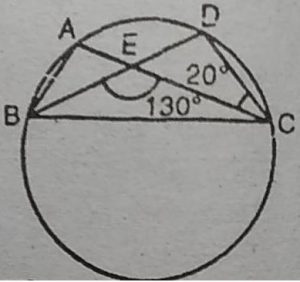
हल: ∠CED + ∠CEB = 180° [रैखिक युग्म]
⇨ ∠CED+ 130° = 180°
⇨ ∠CED = 180° – 130º = 50°
∆ECD में,
∠EDC + ∠CED + ∠ECD =180°
⇨ ∠EDC+50° +20° = 180°
⇨ ∠EDC = 180°-50° -20° = 110°
⇨ ∠BDC = ∠EDC = 110°
चूँकि एक ही वृत्तखंड में कोण बराबर होते हैं।
.: ∠BAC = ∠BDC= 110°
6. ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं।
यदि ∠DBC = 70° और ∠BAC=30° हो, तो ∠BCD ज्ञात कीजिए । पुनः यदि AB
= BC हो, तो ∠ECD ज्ञात कीजिए।
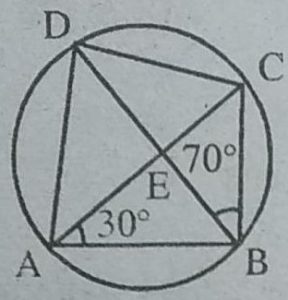
हल: ∠BDC = ∠BAC [एक ही वृत्तखंड के कोण]
⇨ ∠BDC = 30° [चूँकि ZBAC = 30° (दिया है)।]
∆BCD में,
∠BDC+∠DBC+∠BCD = 180° [त्रिभुज के तीनों कोणों का
योग 180° होता है।]
⇨ 30° +70° +∠BCD = 180° [ चूँकि ∠DBC = 70°, ∠BDC = 30°]
⇨ ∠BCD = 180°-30°-70° = 80°
यदि AB = BC, तब ∠BCA = ∠BAC=30°
[त्रिभुज में बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
अब, ∠ECD = ∠BCD-∠BCE= 80°-30° = 50°
[ चूँकि ∠BCD = 80° (ऊपर पाया है) तथा ∠BCE = ∠BCA = 30°]
अत: ∠BCD = 80° और ∠ECD=50°.
7. यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से होकर जाने वाले वृत्त के व्यास
हों, तो सिद्ध कीजिए कि वह एक आयत है।
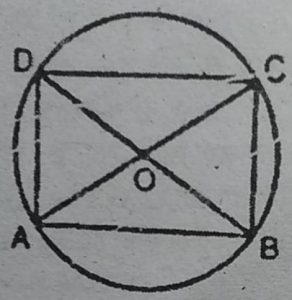
हल : एक चक्रीय चतुर्भुज के विकर्ण AC तथा BD
एक ही वृत्त के व्यास हैं जो चतुर्भुज ABCD के
शीर्ष A,B,C तथा D हैं।
सिद्ध करना है : चतुर्भुज ABCD एक आयत है।
प्रमाण : चूँकि एक वृत्त की सभी त्रिज्याएँ बराबर
होती हैं।
.: OA =OB = OC = OD
⇨ OA = OC = 1/2 AC
तथा OB = OD = 1/2 BD
⇨ AC = BD
.: चतुर्भुज ABCD के विकर्ण बराबर हैं तथा एक-दूसरे को समद्विभाजित करते हैं।
⇨ चतुर्भुज ABCD एक आयत है।
8. यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय
है।
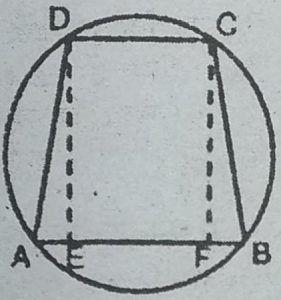
हल : दिया है : एक समलम्ब की असमान्तर
रेखाएँ AD तथा BC बराबर हैं।
सिद्ध करना है : ABCD एक चक्रीय समलम्ब है।
रचना : DE ⊥ AB तथा CF ⊥ AB खींचें।
प्रमाण : यह सिद्ध करने के लिए कि ABCD एक
चक्रीय समलम्ब है, यह पर्याप्त है कि ∠B+ ∠D =180° सिद्ध किया जाए।
∆DEA तथा ∆CFB में,
AD = BC (दिया है)
∠DEA = ∠CFB [प्रत्येक = 90°]
तथा DE = CF
[दो समानांतर रेखाओं के बीच की दूरी बराबर होती है।]
.: RHS सर्वांगसम गुणधर्म से,
∆DEA≈∆CFB
⇨ ∠A = ∠B तथा ∠ADE= ∠BCF
अब ∠ADE = ∠BCF
⇨ 90° + ∠ADE = 90° + ∠BCF
⇨ ∠EDC + ∠ADE = ∠FCD + ∠BCF
[चूँकि ∠EDC = 90° तथा ∠FCD = 90°]
⇨ ∠ADC = ∠BCD
⇨ ∠D = ∠C
इसलिए, ∠A = ∠B तथा ∠C= ∠D
.: ∠A+ ∠B+ ∠C+ ∠D= 360°
[चूँकि एक चतुर्भुज के कोणों का योग 360° होता है।]
⇨ 2∠B+2∠D = 360°
⇨ ∠B+ ∠D = 180°
अत: ABCD एक चक्रीय समलम्ब है।
9. दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते
हैं। B से जाने वाले दो रेखाखंड ABD और PBQ
वृत्तों को A,D और P, Q पर क्रमशः प्रतिच्छेद
करते हुए खींचे गए हैं (देखिए आकृति)। सिद्ध
कीजिए कि ∠ACP = ∠QCD हैं।
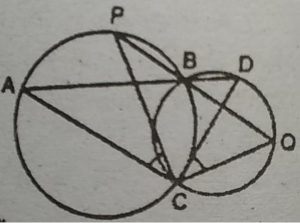
हल : चूँकि एक ही वृत्तखंड के कोण बराबर होते हैं।
.: ∠ACP = ∠ABP …..(1)
तथा ∠QCD = ∠QBD ….(2)
और ∠ABP = ∠QBD …..(3) [शीर्षाभिमुख कोण]
.: समी. (1),(2) तथा (3) से,
∠ACP = ∠QCD.
10. यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचा जाए, तो सिद्ध
कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
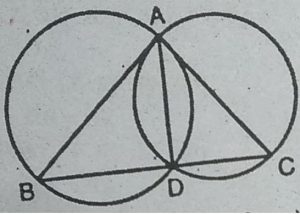
हल : दिया है : ∆ABC की भुजाएँ AB तथा
AC को व्यास लेते हुए दो वृत्त बनाए गए हैं। वृत्त
एक-दूसरे को A तथा D बिन्दु पर प्रतिच्छेदित
करते हैं।
सिद्ध करना है : D, BC पर स्थित है।
रचना : A तथा D को मिलाया।
प्रमाण : चूँकि AB तथा AC दो वृत्तों के व्यास है। [दिया है।]
.: ∠ADB = 90° [अर्धवृत्त में बने कोण]
तथा ∠ADC = 90° [अर्धवृत्त में बने कोण]
जोड़ने पर, ∠ADB+ ∠ADC = 90° + 90° = 180°
⇨ BDC एक सीधी रेखा है।
अत: D, EC पर स्थित है।
11. उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं । सिद्ध कीजिए
कि ∠CAD = ∠CBD है।
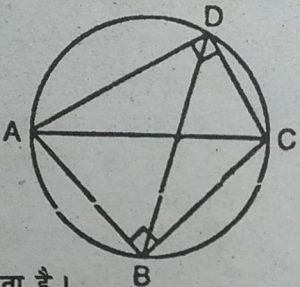
हल : उभयनिष्ठ कर्ण AC को व्यास लेकर खींचा
गया वृत्त, बिन्दु B तथा D दोनों से गुजरता है।
[चूँकि ZABC = LADC = 90° है।]
स्पष्ट रूप से ∠CAD = ∠CBD
[चूँकि एक ही खंड में स्थित कोण समान होते हैं।]
12. सिद्ध कीजिए कि चक्रीय समांतर चतुर्भुज आयत होता है।
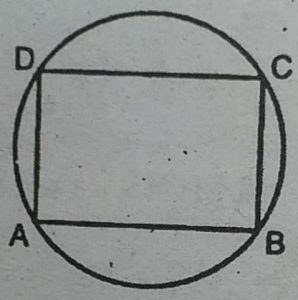
हल : दिया है : ABCD एक समान्तर चतुर्भुज है जो कि एक वृत्त के अन्दर है।
सिद्ध करना है : ABCD एक आयत है।
प्रमाण : चूँकि ABCD एक चक्रीय चतुर्भुज है।
.: ∠A+∠C= 180° ….(1)
लेकिन ∠A=∠C …(2)
समी. (1) तथा (2) से,
∠A = ∠C=90°
इसी प्रकार,
∠B+∠D=90°
.: ABCD का प्रत्येक कोण 90° है।
अत: ABCD एक आयत है।
प्रश्नावली 10.6 (ऐच्छिक)
1. सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों की केन्द्रों की रेखा दोनों प्रतिच्छेद
बिन्दुओं पर समान कोण अंतरित करती है।
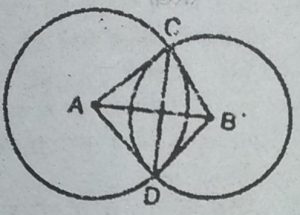
हल : दिया है : दो वृत्त, केन्द्र A तथा केन्द्र B के साथ जो कि एक-दूसरे को C तथा
D पर काटते हैं।
सिद्ध करना है : ∠ACB = ∠ADB
रचना : AC,AD, BD तथा BC को मिलाया।
उपपत्ति: ∆ACB तथा ∆ADB में
AC = AD
[एक ही वृत्त की त्रिज्याएँ]
BC = BD
[एक ही वृत्त की त्रिज्याएँ।]
AB = AB [उभयनिष्ठ]
.: SSS सर्वांगसम गुणधर्म से,
∆ ACB = ∆ ADB
⇨ ∠ACB = ∠ADB [सर्वांगसम त्रिभुजों के संगत भाग]
2. एक वृत्त की 5cm तथा 11 cm लम्बी दो जीवाएँ AB और CD समांतर हैं और केन्द्र
की विपरीत दिशा में स्थित हैं। यदि AB तथा CD के बीच की दूरी 6 cm हो, तो
वृत्त की त्रिज्या ज्ञात कीजिए।
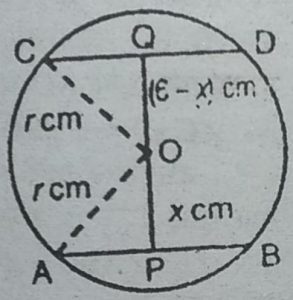
हल : माना O दिए गए वृत्त का केन्द्र है तथा इसकी
त्रिज्या rcm है। OP ⊥AB तथा OQ⊥CD
डाला। चूंकि OP ⊥ AB, OQ ⊥ CD तथा AB ||
CD है, इसलिए बिन्दु P,O तथा Q संरेखी हैं।
इसलिए PQ=65 cm.
माना OP = x. तब OQ= (6-x) cm
OA तथा OC को मिलाया।
तब OA =OC=r
चूँकि केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।
.: AP= PB = 2.5 cm तथा CQ = QD = 5.5 cm.
समकोण ∆OAP तथा ∆OCQ में,
OA² = OP² + AP² तथा OC² = OQ² + CQ²
⇨ r² = x² + (2.5)² …..(1)
तथा r² = (6-x)² + (5.5)² …(2)
⇨ x² + (2.5)² = (6 – x)² + (5.5)²
⇨ x²+ 6.25 = 36 – 12x + x² + 30.25
⇨ 12x = 60 ⇨ x= 5
समी. (1) में x=5 रखने पर,
r² = 5²+ (2.5)² = 25+ 6.25 = 31.25
⇨ r = √31.25 = 5.6 (लगभग)
अतः वृत्त की त्रिज्या 5.6 cm (लगभग)
3. किसी वृत्त की दो समांतर जीवाओं की लम्बाइयाँ 6 cm और 8cm हैं। यदि छोटी जीवा
केन्द्र से 4 cm की दूरी पर हो, तो दूसरी जीवा केन्द्र से कितनी दूर है ?

हल : माना केन्द्र O वाले वृत्त की AB तथा CD दो समांतर जीवाएँ इस प्रकार हैं कि
AB = 6cm तथा CD=8cm
माना वृत्त की त्रिज्या = r cm है।
OP ⊥ AB तथा OQ⊥CD डाला । चूँकि AB ||CD
तथा OP ⊥ AB, OQ ⊥CD. इसलिए बिन्दु O,Q
तथा P संरेखी हैं। स्पष्ट रूप से OP=4 cm तथा P,
Q क्रमशः AB तथा CD के मध्य बिन्दु है।
.: AD = PB = 1/2 AB = 3 cm
तथा, CQ = QD = 1/2 CD = 4cm
समकोण ∆OAP में, OA² = OP² + AP²
⇨ r² = 4²+3²= 16+ 9 = 25
⇨ r = 5
समकोण ∆OCQ में, OC² = OQ² + CQ²
⇨ r²= OQ² +4²
⇨ 25 = OQ² +16
⇨ OQ² = 9
⇨ OQ = 3
अतः केन्द्र से जीवा की दूरी 3 cm है।
4. मान लीजिए कि कोण ABC का शीर्ष एक वृत्त के दूर स्थित है और कोण की भुजाएँ
वृत्त से बराबर जीवाएँ AD और DE काटती हैं। सिद्ध कीजिए कि ∠ABC जीवाओं
AC तथा DE द्वारा केन्द्र पर अंतरित कोणों के अंतर का आधा है।

हल : चूंकि त्रिभुज के बहिकोण का योग अभ्यन्तर अन्तः कोणों के बराबर होता है।
∠ABC में, ∠ADC = ∠DBC + ∠DCB ….(1)
चूंकि केन्द्र पर बना कोण वृत्त के बाकी बचे हुए किसी भी हिस्से में बने कोण का दो गुना
होता है।
.: ∠ADC= 1/2 ∠AOC तथा ∠DCB = 1/2 ∠DOE ….(2)
समी. (1) और (2) से, 1/2 ∠AOC = ∠ABC + 1/2 ∠DOE [चूंकि ∠DBC = ∠ABC]
⇨ ∠ABC = 1/2(∠AOC – ∠DOE)
अत: ∠ABC जीवाओं AC तथा DE द्वारा केन्द्र पर अंतरित कोणों के अन्तर का आधा है।
5. सिद्ध कीजिए कि किसी समचतुर्भुज की किसी भुजा
को व्यास मानकर खींचा गया वृत्त उसके विकर्णों के
प्रतिच्छेद बिन्दु से होकर जाता है।
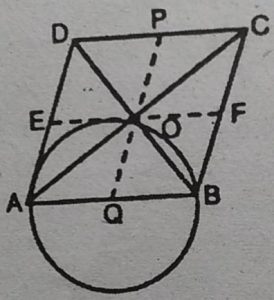
हल : दिया है : ABCD एक समचतुर्भुज है।
AC तथा BD इसके दो विकर्ण हैं जो कि एक
दूसरे को समकोण पर काटते हैं।
सिद्ध करना है : AB को व्यास लेते हुए बनाया
गया वृत्त O से होकर गुजरेगा।
रचना : O से PQ ||AD तथा EF ||AB खींचा।
उपपत्ति: .: AB = DC
⇨ 1/2 AB = 1/2 DC
⇨ AQ = DP [चूंकि Q तथा P, AB तथा CD के मध्य बिन्दु हैं।]
इसी प्रकार से, AE = QQ
⇨ AQ = OQ = QB
⇨ Q को केन्द्र लेते हुए बनाया गया वृत्त A, O तथा B से होकर गुजरता है और इसकी
त्रिज्या AQ है।
इसीलिए प्राप्त किया गया वृत्त ही अभीष्ट वृत्त है।
6. ABCD एक समांतर चतुर्भुज है। A, B और C से जाने वाला वृत्त CD (यदि
आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE
= AD है।
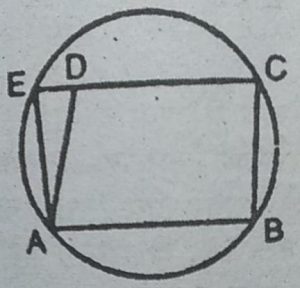
हल : यह सिद्ध करने के लिए कि AE = AD
अर्थात् ∆ AED एक समद्विबाहु त्रिभुज है। यह
पर्याप्त है कि सिद्ध किया जाए कि ∠AED =
∠ADE चूंकि ABCE एक चक्रीय चतुर्भुज है।
.: ∠AED+ ∠ABC = 180° …(1)
अब, CDE एक सीधी रेखा है।
⇨ ∠ADE + ∠ADC =180° ….(2)
[चूंकि LADC और ZABC समांतर चतुर्भुज के सम्मुख
कोण हैं अर्थात् ∠ADC = ∠ABC]
समी. (1) और (2) से,
∠AED + ∠ABC = ∠ADE + ∠ABC
⇨ ∠AED = ∠ADE
.: ∆ AED में, ∠AED = ∠ADE
⇨ AD = AE.
7. AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित करती हैं। सिद्ध
कीजिए
(i) AC और BD व्यास हैं।
(ii) ACBD एक आयत है।
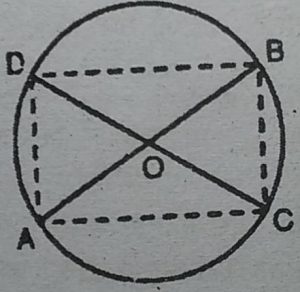
हल : (i) माना केन्द्र O वाले एक वृत्त की AB तथा
CD दो जीवाएँ हैं।
माना कि वह एक-दूसरे को O पर काटती हैं।
AC, ED, AD तथा BC को मिलाया।
∆AOC तथा ∆BOD में,
AD = OB [चूंकि O,AB का मध्य बिन्दु है।]
∠AOC = ∠BOD [शीर्षाभिमुख कोण]
तथा OC = OD [चूंकि O,CD का मध्य बिन्दु है।]
.: SAS सर्वांगसमता गुणधर्म से,
∆AOC≈∆BOD
⇨ AC = BD
⇨ AC = BD ….(1)
इसी प्रकार,∆AOD तथा ∆ BOC से
AD = BC ….(2)
समी. (1) तथा (2) से,
AC+AD = BD+ BC
⇨ CAD = CBD
⇨ CD वृत्त को दो भागों में बाँटती है।
⇨ CD एक व्यास है।
इसी प्रकार, AB एक व्यास है।
(ii) चूँकि ∆AOC ≈ ∆BOD [ऊपर सिद्ध किया गया है।]
⇨ ∠OAC अर्थात् ∠BAC = ∠OBD अर्थात् ∠ABD
⇨ AC∥ BD
पुनः, ∆ AOD ≈∆COB
⇨ AD∥ CB
⇨ ACBD एक चक्रीय समांतर चतुर्भुज है।
⇨ ∠DAC = ∠DBA ….(3)
[समांतर चतुर्भुज के सम्मुख कोण समान होते हैं।]
ACBD एक चक्रीय चतुर्भुज है।
.: ∠DAC+∠DBA = 180° …..(4)
(3) तथा (4) से, ∠DAC= ∠DBA = 90°
अत: ACBD एक आयत है।
8. एक त्रिभुज ABC में कोणों A, B और C के समद्विभाजक इसके परिवृत्त को क्रमशः
D,E और F पर प्रतिच्छेद करते हैं । सिद्ध कीजिए कि त्रिभुज DEF के कोण 90°
-1/2A, 90° -1/2B तथा 90° – 1/2C हैं।
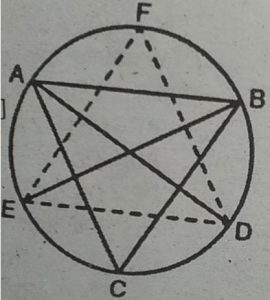
हल : ∠D=∠EDF= ∠EDA + ∠ADF
=∠EBA + ∠FCA
[चूँकि ∠EDA और ∠EBA एक ही वृत्तखंड में कोण हैं।]
.: ∠EDA =∠EBA
इसी प्रकार से ∠ADF तथा ∠FCA भी वृत्त के
एक ही वृत्तखंड के कोण हैं। अतः
∠ADF = ∠FCA
= 1/2 ∠B+1/2 ∠C
[चूँकि BC, ∠B का अभ्यंतर कोण समद्विभाजक है तथा CF, ∠C का अभ्यंतर कोण
समद्विभाजक है।]
= ∠B+∠C/2
इसी प्रकार से,
∠E =∠C+∠A/2 तथा ∠F = ∠A+∠B/2
⇨ ∠D =180°-∠A/2, ∠E=180°-∠B/2
तथा ∠F =180° – ∠C/2 [ चूँकि ∠A+ ∠B+ ∠C= 180°]
⇨∠D = 90° – ∠A/2,
∠E = 90°- ∠B/2 तथा ∠F= 90° – ∠C/2
⇨∆DEF के कोण 90° – 1/2 A,90° – 1/2B तथा 90°- 1/2C हैं।
9. दो सर्वांगसम वृत्त परस्पर को बिन्दुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई
रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं। सिद्ध
कीजिए कि BP = BQ है।
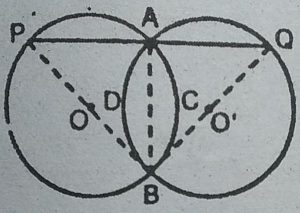
हल : माना 0 तथा O’ दो सर्वांगसम वृत्तों के केन्द्र हैं।
चूँकि AB इन वृत्तों की उभयनिष्ठ जीवा है।
.: चाप ACB= चाप ADB
⇨ ∠BPA = ∠BQA
⇨ BP = BQ.
10. किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लम्ब समद्विभाजक
प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
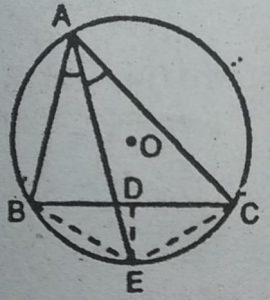
हल : दिया है : O केन्द्र वाले एक वृत्त के अन्दर
ABC एक त्रिभुज है। E वृत्त पर एक बिन्दु इस
प्रकार है कि AE, ∠BAC का अभ्यंतर कोण
समद्विभाजक है तथा D, EC का मध्य बिन्दु है।
सिद्ध करना है : DE, BC का कोण समद्विभाजक है।
अर्थात् ∠BDE= ∠CDE = 90°.
रचना :BE तथा EC को मिलाया।
उपपत्ति: ∆BDE तथा ∆CDE में,
BE=CE [ चूँकि ∠BAE= ∠CAE, .: चाप BE= चाप. CE ⇨ जीवा BE= जीवा CE]
BD = CD [दिया है।]
DE = DE [उभयनिष्ठ]
.: SSS सर्वांगसमता गुणधर्म से,
∆ BDE ≈ ∆ CDE
⇨ ∠BDE = ∠CDE [C.P.C.T.]
तथा ∠BDE+∠CDE = 180° [रैखिक युग्म]
.: ∠BDE = ∠CDE= 90°
अत: DE, BC का समकोण समद्विभाजक है।
◆◆◆
