BIHAR BOARD CLASS 8TH MATH | घन और घनमूल
BIHAR BOARD CLASS 8TH MATH | घन और घनमूल
घन सं० = जब हम किसी सं० को स्वयं से तीन बार गुणा करते हैं तो प्राप्त सं० को हम
घन संख्या कहते हैं।
अर्थात् a का घन सं० = a×a×a = a³
जैसे 2 का घन =2×2×2 =8
3 का घन = 3×3×3=27
4 का घन =4×4×4 = 64
स्वयं करके देखिए-
(i) 543 =7×7×7 = 3√7
729 =9×9×9= 3√9
निम्नलिखित में से कौन-सी सं. पूर्ण घन हैं-
(i) 216 (ii) 8000


=2×2×2×3×3×3. = 2×2×2×2×2×2×5×5×5
= 2×3=6 (पूर्ण घन है) =2×2×5 = 20 (पूर्ण घन है)
(iii) 800 (iv) 15625


= 2×2×2×2×2×5×5 = 5×5×5×5×5×5
(पूर्ण घन है) = 25 (पूर्ण घन है)
प्रश्नावली-6.1
1. निम्नलिखित में से कौन-सी संख्याएँ पूर्ण घान नहीं हैं-
(i) 400 (ii) 342 (iii) 68600 (iv)2744
(v) 800 (vi)46656 (vi)408375 (viii) 9000
उत्तर- (i)400 (ii) 342


=2×2×2×2×5×5 =7×7×7
= पूर्ण घन नहीं है। = यह एक पूर्ण घन है।
(iii) 68600 (iv) 2744


= 2×2×2×5×5×7×7×7 = 2×2×3×5×5×5×11×11
(यह एक पूर्ण घन नहीं है।) (एक पूर्ण घन नहीं है।)
(v) 800 (vi)46656


= 2×2×2×2×2×5×5 = 2×2×2×3×3×5×5×5
(यह एक पूर्ण घन नहीं है।) (यह एक पूर्ण घन नहीं है।)
(vii)800 (viii) 9000


= 3×3×3×5×5×11×11 = 2×2×2×3×3×5×5×5
(यह एक पूर्ण घन नहीं है।) (यह एक पूर्ण घन नहीं है।)
2. वह सबसे छोटी संख्या ज्ञात करें जिसे निम्नलिखित संख्याओं से गुणा करने पर पूर्ण
घन प्राप्त हो जाए―
(i) 320 (ii) 243 (iii) 675 (iv)432
उत्तर―
(i) 320 (ii) 243
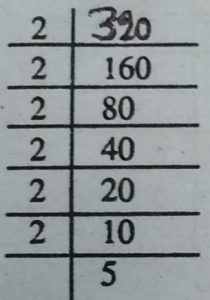
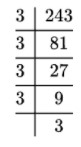
= 2×2×2×2×2×2×5×2×2 = 3×3×3×3×3×?
.: 5×5 = 3
(iii) 675 (iv) 432
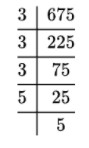

= 3×3×3×5×5×?=5 = 2×2×2×3×3×3×2×2×?
= 2 = 11×2=22
3. वह छोटी सी छोटी संख्या ज्ञात करें जिसे निम्नलिखित संख्याओं से भाग देने पर भागफल एक पूर्ण घन प्राप्त हो जाए-
(i) 256 (ii) 3125 (iii) 1408 (iv) 192
उत्तर―
(i) 256 (ii) 3125

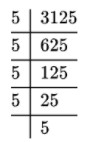
=2×2×2×2×2×2×2×2 = 2×2×2×2×2×2×2×11
=2×2=4 = 23
(iii) 1408 (iv) 192

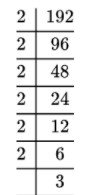
=5×5×5×5×5= 2×2=4 =2×2×2×2×2×2×3=3
4. निम्नलिखित घन संख्या को उसके क्रमागत विषम संख्याओं के योग के रूप में लिखें-
(i) 2³ (ii) 4³ (iii) 5³ (iv) 8³
उत्तर—
(i) 2³ =2×2×2 = 8 = 3+5=8
(ii) 4³=4×4×4= 64
= 13 + 15 + 17 + 19 = 64
(iii)5³ =5×5×5= 125
= 21 +23+25+27 +29 = 125
(iv) 8³ =8×8×8 = 164
= 57 +59 +61 +63 +65 +67+ 69 + 71 = 164
घनमूल (Cuberoot)—एक ऐसी संख्या जिसका घन ज्ञात हो घनमूल कहलाता है।
जैसे-5³ = 125
अर्थात् 125 का घनमूल 5 है।
सांकेतिक रूप में हमें 3√ लिखते हैं।
प्रश्नावली-6.2
1. निम्नलिखित में से प्रत्येक संख्या का घनमूल अभाज्य गुणनखंडन विधि से ज्ञात करें ।
(i) 125 (ii) 729 (iii) 512 (iv) 1331
(v) 5832. (vi) 421875 (vii) 157464 (viii) 74088
(ix) 175616 (x) 35937
उत्तर—
(i) 125 (ii) 729
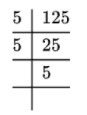

=5×5×5=5³ =3×3×3×3×3×3
(iii) 512 (iv) 1331

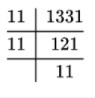
= 2×2×2×2×2×2×2×2×2. ³√11³ = 11
= 2³x2³x2³
= 2×2×2=8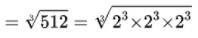
(v) 5832 (vi) 421875


=2×2×2×3×3×3×3×3×3 = 3×3×3×5×5×5×5×5×5
=2³×3³×3³ =3³×5³×5³
= ³√5832. = ³√421875 = ³√3³ × ³√5³ × ³√5³
= ²√2³×²√3³×²√3³. =3×5×5= 75
= 2×3×3=18
(vii) 157464
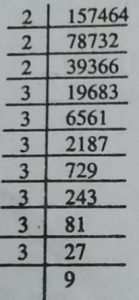
=2×2×2×3×3×3×3×3×3×3×3×3
= ³√157464 =³√2³×³√3³ ׳√3³ ׳√3³
= 2×3×3×3=54
(viii) 175616

= 2×2×2×2×2×2×2×2×2×7×7×7
= ³√175616 =√2³×√2³×√2³×√7³
(ix) 35937
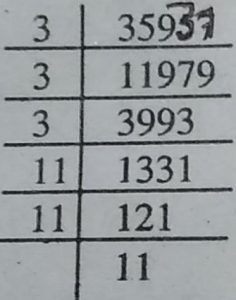
√35937 = √3³×√11³ = 3 ×11 = 33
2. निम्नलिखित में से प्रत्येक संख्या के लिए वह छोटी-से-छोटी संख्या बताएँ जिससे इस
संख्या को गुणा करने पर वह एक पूर्ण घन बन जाए। इस प्रकार से प्राप्त पूर्ण धन
संख्या का घनमूल भी ज्ञात करें।
(i) 320 (ii) 1352 (iii) 243 (iv) 675 (v) 432
उत्तर―
(i) 320

= 2×2×2×2×2×2×5
प्राप्त छोटी सं० = 5
प्राप्त पूर्ण घन सं० = 320×5×5 = 8000
प्राप्त पूर्ण सं० का घनमूल

= 2×2×2×2×2×2×5×5×5
=2×2×5= 20
(ii) 1352

=2×2×2×13×13
प्राप्त छोटी सं. = 13
प्राप्त पूर्ण घन सं. = 1352×13 = 17576
(iii) 243
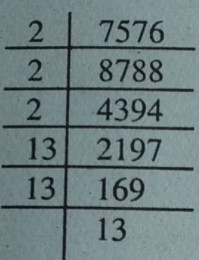
= 2×2×2×13×13×13
=2×13 =26
(iv) 675


3×3×3×5×5 =3×3×3×5×5×5
.: प्राप्त छोटी सं० =5 =3×5= 15
पूर्ण घन सं. = 675×5 = 3375
3. वह छोटी सी छोटी संख्या ज्ञात करें जिससे निम्नलिखित संख्याओं को भाग देने पर
वह एक पूर्ण घन बन जाए । इस प्रकार से प्राप्त पूर्ण घन संख्या का घनमूल भी ज्ञात करें।
(i) 256 (ii) 3125 (iii) 8019 (iv)1408 (v) 192
उत्तर―
(i) 256


2×2×2×2×2×2×2×2×2 2×2×2×2×2×2=2×2=4
उक्त सं० = 2
प्राप्त पूर्ण सं० = 256÷ 4 = 64
(ii) 3125

5×5×5×5×5
उक्त सं० = 3125÷5 = 625
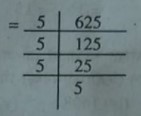
=5×3=15
(iii) 8019


=3×3×3×3×3×3×11 3×3×3×3×3×3=3×3
उक्त सं० =11
अतः प्राप्त पूर्ण सं० = 8019÷11 = 729
(iv) 1408
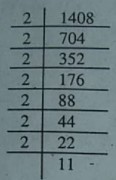
=2×2×2×2×2×2×2×11
उपर्युक्त सं० = 11×2 = 22
1408 ÷ 22 = 64

2×2×2×2×2×2=2×2=4
(v) 192

= 2×2×2×2×2×2×3
उपर्युक्त सं० = 3 = 192÷3 = 64

=2×2×2×2×2×2=2×2
4. अनुमान द्वारा निम्नलिखित घन संख्या का घनमूल ज्ञात करें।
(i) 5832 (ii) 74088 (iii) 421875 (iv) 157464
(v)4913 (vi) 12167 (vii) 32768
उत्तर―छात्र स्वयं करें।
5. निम्नलिखित में सत्य और असत्य को बताएँ।
क. किसी भी विषम संख्या का घन सम होता है।
ख. एक पूर्ण घन दो शून्यों पर समाप्त नहीं होता है।
ग. यदि किसी संख्या का वर्ग 5 पर समाप्त होता है तो उसका घन 25 पर समाप्त
होता है।
घ. ऐसा कोई पूर्ण घन नहीं है जो 8 पर समाप्त होता है।
ङ. दो अंकों की संख्या का घन तीन अंकों वाली संख्या हो सकती है।
च. दो अंकों की संख्या के घन में सात या अधिक अंक हो सकते हैं।
छ. एक अंक वाली संख्या का घन एक अंक वाली संख्या हो सकती है।
उत्तर-(क) असत्य, (ख) सत्य, (ग) असत्य, (घ) असत्य, (ङ) असत्य,
(च) असत्य, (छ) सत्य।
■