BIHAR BOARD CLASS 8TH MATH | वर्ग और वर्गमूल
BIHAR BOARD CLASS 8TH MATH | वर्ग और वर्गमूल
वे संख्याएँ जो समान पंक्ति व स्तम्भ के रूप में जगाई जा सकती है पूर्ण वर्ग संख्याएँ
कहलाती हैं।
जैसे 9–

पूर्ण वर्ग संख्याएँ पहचानने का एक और तरीका अभाज्य गुणनखड विधि है।
किसी संख्या का अभाज्य गुणनखंड तरीके से गुणनखंडन करने से अगर गुणनखंडों के
पूरे–पूरे जोड़े बन जाएँ तो वह संख्या पूर्ण वर्ग संख्या होती है।
जैसे–256

= 2×2×2×2×2×2×2×2
=2×2×2×2
=2×2×2×2 = 16
अर्थात् 256, 16 का वर्ग है।
स्वयं करके देखिए-
1. क्या निम्नलिखित संख्याएँ पूर्ण वर्ग हैं ?
(i) 400
उत्तर–

=2×2×2×25×5
=2×2×5=20
हाँ ये पूर्ण वर्ग है।
(ii) 600
2x2x2x3x5x5
यहाँ पूर्ण जोड़े नहीं बन रहे हैं
.: यह पूर्ण वर्ग नहीं है।
दी गई संख्याओं के बीच की पूर्ण वर्ग संख्याएँ ज्ञात करें।
(i) 20 और 30
उत्तर-

20=2×2×5
30=2×3×5

21=3×7
22=2×11
23=23×1

24= 2×2×3×2
25 = 5×5
26 =2×13

27 = 3×3×3
28 =2×2×7
29=29×1
20 और 30 के बीच की पूर्ण वर्ग सं० = 25
(ii) 50 और 60
उत्तर–50 और 60 के बीच की पूर्ण वर्ग संख्याएँ-

50 =2×5×5
60= 2×2×3×5
51=1×51

52 = 2×2×13
53 =1×53
54 = 2×3×3×3
55=11×5
56 =2×2×2×7
58=2×29
59=1×59

50 और 60 के बीच कोई भी पूर्ण वर्ग संख्या नहीं है।
3. रिक्त स्थानों की पूर्ति कीजिए–
क्र.सं. संख्या अ•गु• क्या जोड़े बन रहे हैं पूर्ण वर्ग है/नहीं
1. 36 2×2×3×3 हाँ हाँ
2. 32 2×2×2×2×2 नहीं नहीं
3. 16 2×2×2×2 हाँ हाँ
4. 39 3×13 नहीं नहीं
5. 40 2×2×2×5 नहीं नहीं
6. 49 7×7 हाँ हाँ
7. 56 2×2×2×7 नहीं नहीं
8. 64 2×2×2×2×2×2 हाँ हाँ
वर्ग संख्याओं के गुणधर्म– जिस संख्या के इकाई के स्थान पर 2, 3,7 तथा 8 है वह संख्या कभी भी पूर्ण वर्ग नहीं हो सकती है।
जैसे–52, 12,22, 32
सम संख्याओं के वर्ग सम तथा विषम संख्याओं के वर्ग विषम होते हैं।
किसी संख्या में शून्य की संख्या जितनी हो उसके वर्ग में शून्य की संख्या दुगुनी
होती है। जैसे–
10² = 100
100² = 10000
नियम= (n5)² = (10n +5)² = 100n+ 100n + 25
= 100n (n+1)+25 =n (n+ 1) 100+25
पाइथागोरस त्रिक–ऐसी संख्याएँ जिनमें दो संख्याओं के वर्गों का जोड़ तीसरी वर्ग संख्या के बराबर हो, पाइथागोरस त्रिक कहलाते हैं।
अर्थात् a²+b² = c²
3² +4² = 5²
9+16 = 25
25 = 25
[प्रश्नावली-5.1]
1. निम्नलिखित सं• का वर्ग ज्ञात करें।
(i) 42 (ii) 46 (iii) 58 (iv) 98 (v) 94 (vi) 45
उत्तर-


8836 2025
2. निम्नलिखित का वर्ग निकालें।
(i) 25 (ii) 55 (iii) 95 (iv) 105 (v) 115
उत्तर-


3. निम्नलिखित संख्याओं में से कौन-सी संख्याएँ पूर्ण वर्ग हैं ? जाँच कीजिए।
(i) 256 (ii) 360 (iii) 324 (iv) 400
उत्तर-
(i) 256 (ii) 360


=2×2×2×2×2×2×2×2 =2×2×2×3×3×5
=2×2×2×2 = 16 = पूर्ण सं• नहीं है।
(iii) 32 (iv) 400


=2×2×9×9 = 2×2×2×2×5×5
=2×9 = 18 (पूर्ण वर्ग है) =2×2×5 = 20 (पूर्ण वर्ग है)
4. निम्नलिखित संख्याओं में से कौन-कौन पूर्ण वर्ग हैं ?
13, 16, 17, 48, 49, 64, 72, 343, 373758
उत्तर–
13 = 13×1 (पूर्ण वर्ग नहीं है)
16 = 2×2×2×2 = 2×2 = 4 (पूर्ण वर्ग है)
17 = 1×17 (पूर्ण वर्ग नहीं है)
48 = 2×2×2×2×3 (पूर्ण वर्ग नहीं है)
49 = 7×7 (पूर्ण वर्ग है)
64 = 2×2×2×2×2 = 2×2×2 (पूर्ण वर्ग है)
72 = 2×2×2×3×3 (पूर्ण वर्ग नहीं है)
343 =7×7×7 (पूर्ण वर्ग नहीं है)
337358 =2×3×7×11× 809 (पूर्ण वर्ग नहीं है)
5. निम्नलिखित में कौन सम संख्या के वर्ग हैं?
169, 196, 256, 1296, 6561
उत्तर– दिए गए संख्याओं में 196,256 तथा 1296 के इकाई स्थान पर सम सं० है।
.: ये सम संख्या के वर्ग हैं।
6. निम्नलिखित संख्याओं में से कौन-सी पूर्ण वर्ग है ?
400, 4000, 330550, 12345600000
उत्तर–
(i) 400 (ii) 4000


=2×2×2×2×5×5 =2×2×2×2×5×5×5
= 2×2×5 = 20 (पूर्ण वर्ग है) = पूर्ण वर्ग नहीं है।
(iii) 330550 (iv) 12345600000

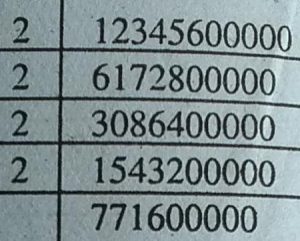
पूर्ण वर्ग नहीं है। इनके अंत में शून्य की सं.
विषम है। यह पूर्ण वर्ग नहीं है।
7. कोष्ठक में सही संख्या लिखें:
(a) 24²-23² = [ ] (b) 102² – 101² = [ ]
(c) 501² – 500² = [ ] (d) 400²-399² = [ ]
उत्तर-
(a) 24²-23² (b) 12²-101²
= (24 +23) (24-23) = (102 + 101) (102 – 101)
=47×1=47 =203×1=203
(c) 501²-500² (d) 400-399
= (501 +500) (501 – 500) = (400 + 399) (400 – 399)
= 1001×1= 1001 =799×1 =799
8. निम्नलिखित में कौन-सा त्रिक पाइथागोरस त्रिक है?
(1,2,3), (3,4,5), (6, 8, 10), (1, 1, 1), (2,2,3), (15, 36, 39)
उत्तर–पाइथागोरस त्रिक =a²+b²=c²
(1,2,3) = 1²+2=3² = 1+4≠9(पाइथोगरस त्रिक नहीं है)
(3,4,5) =3²+4² = 5² =9+ 16 = 25 = 25 = 25 (पाइथोगोरस त्रिक है)
(6,8,10) = 6² +8² = 10² = 36 + 64 = 100
= 100 = 100 (पाइथागोरस त्रिक है)
(1,1,1) = 1² + 1² = 1² = 1 + 1 = 1
= 2≠1 (पाइथागोरस त्रिक नहीं है)
(2,2,3) = 2² +2² = 3² = 4+4= 9
=8≠9(पाइथागोरस एक त्रिक नहीं है)
(15, 36, 39) = 15² + 36² = 39² = 225 + 1296 = 1521
= 1521 = 1521 (पाइथागोरस त्रिक है)
9. निम्नलिखित प्रतिरूप का प्रेक्षण करके छुटी हुई संख्याओं को ज्ञात करें :
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + …..² + …..² = 21²
5² + 6² + …..² = 31²
6² + 7² + ….. = …….
उत्तर-
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + 5² + 20² = 21²
5² + 6² + 30² = 31²
6² + 7² + 42² = 43²
10. विषम संख्याओं के क्रमिक घटाव की क्रिया द्वारा निम्नलिखित संख्याओं की जाँच करें
कि कौन-सी संख्या पूर्ण वर्ग संख्या है ?
(i) 81 (ii) 121 (iii) 144 (iv)36
उत्तर-
(i) 81 (ii) 121
81 -1 = 80 121 – 1 = 120 यह पूर्ण
वर्ग संख्या है।
80-3 = 77 120 – 3 = 117
77-5= 72 117 – 5 = 112
72-7= 65 यह पूर्ण वर्ग संख्या है। 112-7= 105
105 -9 = 96
65-9 = 56 96 – 11 = 85
56 – 11 = 45 85 – 13 = 72
45 – 13 = 32 72-15 = 57
32 – 15 = 17 57 – 17 = 40
40 – 19 = 21
21-21 = 0
(iii) 144 (iv) 36
36-1 = 35 144 – 1 = 143
35 – 3 = 32 143-3 = 140
32-5= 27 140 – 5 = 135
27-7 = 20 135 – 7 = 128
20-9 = 11 128 -9 = 119
11-11 = 0 119-11 = 108
यह भी एक पूर्ण वर्ग है। 108 – 13 = 95
95 – 15 = 80
80 – 17 = 63
63 – 19 = 44
44-21 = 23
23-23 = 0
यह भी एक पूर्ण वर्ग है।
11. निम्नलिखित संख्याओं में से किन-किन संख्या का वर्ग विषम संख्या होगा?
(i) 531 (ii) 5436 (iii) 3249 (iv) 82004
उत्तर-
531 – वर्ग विषम होगा
5436 – वर्ग सम होगा
3249 – वर्ग विषम होगा
2004 – वर्ग सम होगा
12. योग संक्रिया किये बिना योगफल ज्ञात कीजिए:
(i) 1+3+5+7+9+11
(ii) 1+3+5+ …………+ 51
(iii) 1+3+5+ 7 + ………. + 101
(iv) 7+9+11+13+ …… + 21
उत्तर-
(i) 1+3+5+ 7 + 9 + 11 = 36
(ii) 1+3+5+ ……. + 51 = (26)² = 676
(iii) 1 + 3 + 5 + 7+ …….. 101 = (51)² = 2601
(iv) 7+9+11+13+ …….. +21 = 112
13. निम्नलिखित संख्याओं के वर्गों के इकाई के अंक क्या होंगे?
(i) 25 (ii) 64 (iii) 272 (iv) 799 (v)5423
(vi) 2467 (vii)5438 (viii) 99880 (ix) 43546
उत्तर-
(i) 25 के वर्ग का इकाई का अंक =5
(ii) 64 के वर्ग का इकाई का अंक =6
(iii) 272 के वर्ग का इकाई का अंक =4
(iv) 799 के वर्ग का इकाई का अंक = 1
(v) 5423 के वर्ग का इकाई का अंक =9
(vi) 2467 के वर्ग का इकाई का अंक =9
(vii) 5438 के वर्ग का इकाई का अंक =4
(viii) 99880 के वर्ग का इकाई का अंक =0
(ix) 43546 के वर्ग का इकाई का अंक =6
14. निम्नलिखित संख्याएँ स्पष्ट रूप से पूर्ण वर्ग संख्याएँ नहीं हैं, इसका कारण दीजिए।
(i) 1052 (ii) 23457 (iii) 54328 (iv) 325473
(v) 25000 (vi)743522 (vii)543000 (vii)56430
उत्तर-निम्नलिखित सं० पूर्ण रूप से वर्ग संख्याएँ नहीं है क्योंकि-
(1) 1052– जिन संख्याओं के इकाई स्थान पर 2 हो वो कभी पूर्ण संख्या
नहीं कहलाती।
(ii) 23457– जिन संख्याओं के अंत में 7 होता है वो कभी पूर्ण वर्ग संख्या
नहीं कहलाती।
(iii) 54328– जिन संख्याओं के अंत में 54328 होता है वो कभी पूर्ण वर्ग सं.
नहीं कहलाती।
(iv) 325473–जिन संख्याओं की इकाई की सं० 3 हो वे पूर्ण वर्ग संख्याएँ नहीं होती।
(v) 25000– जिन संख्याओं के अंत में शून्य की संख्या विषम हो वे कभी पूर्ण
वर्ग सं. नहीं होती।
(vi) 743522–जिन संख्याओं के अंत में 2 होता है वे कभी पूर्ण वर्ग सं॰ नहीं होता ।
(vii)543000–जिन संख्याओं के अंत में विषम शून्य संख्याएँ होती हैं वे कभी पूर्ण
वर्ग संख्याएँ नहीं होती हैं।
(viii) 56430–जिन संख्याओं के अंत में विषम शून्य संख्या होती है वे कभी पूर्ण
वर्ग सं नहीं होती है।
भागविधि से वर्गमूल ज्ञात करना–जब संख्याएँ बड़ी होती हैं तब अभाज्य गुणनखंड विधि
द्वारा वर्गमूल ज्ञात करना कठिन होता है। तब हम एक अन्य विधि से गुणनखंड ज्ञान ज्ञात करते
हैं जिसे दीर्घ विभाजन विधि कहते हैं।
यहाँ एक पूर्ण वर्ग सं० में यदि अंक है तो उसके वर्गमूल में n/2 अंक होंगे जब n= सम
सं० हो तथा जब n= विषम हो तब n= n+1/2
उदाहरण के लिए–
144/256 का वर्गमूल ज्ञात करें–


प्रश्नावली-5.2
(i) 625 (ii) 900


(iii) 1444 (iv) 3249


(v) 5776 (vi) 10404


(vii) 19600

2. निम्नलिखित संख्याओं में से प्रत्येक के वर्गमूल में अंकों की संख्या बिना गणना के ज्ञात करें।
(i) 81 (ii) 121 (iii) 256 (iv)4489
(v) 361 (vi)27225 (vii) 390625
उत्तर–81 के वर्गमूल में अंक की सं. =1
121 के वर्गमूल में अंकों की सं० = 42
256 के वर्गमूल में अंकों की सं० = 2
4489 के वर्गमूल में अंकों की सं० =2
361 के वर्गमूल में अंकों की सं० = 2
27225 के वर्गमूल में अंकों की सं० =3
390625 के वर्गमूल में अंकों की सं० =3
3. निम्नलिखित भिन्नों का वर्गमूल ज्ञात करें।

उत्तर–



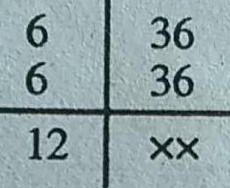





इसका वर्गमूल संभव नहीं।



इसका वर्गमूल संभव नहीं।।
4. निम्नलिखित दशमलव संख्याओं का वर्गमूल ज्ञात करें।
(i) 2.25 (ii) 6.76 (iii) 156.25 (iv)9.8596
(v) 31.36 (vi) 1.816 (vii) 0.2916
उत्तर–
(i) 2.25 (ii) 6.76
 =1.5
=1.5 
(iii) 156.25 (iv) 9.8596


(v) 31.36 (vi) 1.0816


(vii) 0.2916

5. निम्नलिखित संख्याओं में से प्रत्येक में सबसे छोटी-से-छोटी संख्या क्या घटज्ञई
जाए कि पूर्ण वर्ग संख्या प्राप्त हो जाए। इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का
वर्गमूल भी ज्ञात करें।
(i) 90 (ii) 7581 (iii) 1989 (iv)3250 (v)402
(vi) 825 (vii) 4000 (viii)2509
उत्तर-
(i) 90

अभीष्ट सं० = 90–9= 81
अभीष्ट सं० का वर्गमूल

(ii) 7581

अभीष्ट सं. =7581–12 = 7569
अभीष्ट सं का वर्ग मूल

(iii) 1989 (iv) 3250


अभीष्ट सं. = 1989–53 = 1936 अभीष्ट सं. = 3250–1=3249
अभीष्ट सं का वर्गमूल =√1936=44 अभीष्ट सं० का वर्गमूल =√3249=51
(v) 402 (vi) 825


अभीष्ट सं० = 402–2 = 400 अभीष्ट सं. = 825–41 = 784
अभीष्ट सं का वर्गमूल = 20 अभीष्ट सं का वर्गमूल = 28
(vii) 4000 (viii) 2509


अभीष्ट सं० = 4000–31 = 3969 अभीष्ट सं० =2509–9=2500
अभीष्ट सं० का वर्गमूल = 50
6. निम्नलिखित संख्याओं में से प्रत्येक में न्यूनतम संख्या क्या जोड़ी जाए कि वह एक
पूर्ण संख्या बन जाए । इस प्रकार प्राप्त पूर्ण वर्ग संख्याओं का वर्गमूल भी ज्ञात करें।
(i) 130 (ii) 8400 (iii) 6203 (iv) 6412
(v)525 (vi) 1750 (vii) 252 (viii) 1825
उत्तर-(i) 130 (ii) 8400


.: अभीष्ट सं० = 130+ 14 = 144 .: अभीष्ट सं० = 8400+ 64=8464
अभीष्ट सं का वर्गमूल = 12 अभीष्ट सं० का वर्गमूल = 92
(iii) 6203 (iv) 6912


.: अभीष्ट सं.=6203+38=6241 .: अभीष्ट सं० = 6412+149 = 6561
अभीष्ट सं० का वर्गमूल = 79 वर्गमूल = √6561 = 81
(v)525 (vi) 1750


अभीष्ट सं. =525+4=529 अभीष्ट सं० = 1750+14= 1764
वर्गमूल = √529 = 23
(vii) 252 (viii) 1825


अभीष्ट सं. = 252+4= 256 अभीष्ट सं० = 1824+25 = 1849
वर्गमूल = 16 वर्गमूल = 43
7. छः अंकों की वह बड़ी-से-बड़ी संख्या ज्ञात करें जो कि एक पूर्ण वर्ग संख्या है । संख्या
का वर्गमूल भी ज्ञात करें।
उत्तर-

अभीष्ट सं० =999999–1998 = 998001
वर्गमूल = 999
8. चार अंकों की वह बड़ी-से-बड़ी संख्या ज्ञात कीजिए जो कि एक पूर्ण वर्ग संख्या है।
प्राप्त वर्ग संख्या का वर्गमूल भी ज्ञात कीजिए।
उत्तर–चार अंकों की बड़ी सं० = 9999

अभीष्ट सं० = 9999-198 = 9801
वर्गमूल = 99
9. छः अंकों की वह छोटी-से-छोटी संख्या ज्ञात करें कि एक पूर्ण वर्ग संख्या हो । इस
प्रकार से प्राप्त वर्ग संख्या का वर्गमूल भी ज्ञात कीजिए।
उत्तर–छ: अंकों की छोटी सं० = 100000

अभीष्ट सं० = 10000+ 489 = 100489
वर्गमूल = 317
10. एक वर्गाकार मैदान का क्षेत्रफल 60025 m² है। एक आदमी साइकिल से 5 metre
की चाल से मैदान के चारों ओर चलता है तो कितने समय में वह प्रारंभिक बिन्दु पर
आ जाएगा।
उत्तर–

वह आदमी 245 से० में प्रारंभिक बिन्दु पर पहुँचेगा।
◆◆◆
