BIHAR BOARD CLASS 8TH MATH | आँकड़ों का प्रबंधन
BIHAR BOARD CLASS 8TH MATH | आँकड़ों का प्रबंधन
आँकड़ों का प्रबंधन
हम अपने आस-पास की जानकारियों को इकट्ठा कर उनके आँकड़ों को विभिन्न तरीकों
से अपने पास रखते हैं।
इसे इकट्ठा कर अपने कार्यों के अनुरूप इस्तेमाल करना ही आँकड़ा प्रबंधन कहलाता है।
ये विभिन्न प्रकार के होते हैं–
1. चित्रालेख (Pictograph)–इस विधि में संकेतों का प्रयोग करते हुए, आँकड़ों का
चित्रिय निरूपण किया जाता है।
2. दंड आलेख (Bar graphs)–दंड आलेख में प्रत्येक की चौड़ाई समान होती है तथा
वे एक-दूसरे से समान दूरी पर होते हैं। दंड की ऊंँचाई आँकड़ों के अनुसार समानुपातिक होती
है।
3. दोहरे दंड आलेख (Double Bar graphs)–दो समूहों की तुलना करने की
आवश्यकता होती है तो दोहरे दंड आलेख खींचे जाते हैं।
स्वयं करके देखिए–
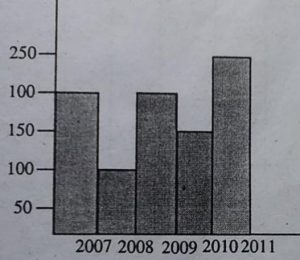
1. अलग-अलग आरेख खींचिए-
वर्ष 2007 2008 2009 2010 2011
पुस्तकालय के लिए खरीदे 190 160 180 150 200
गए पुस्तक
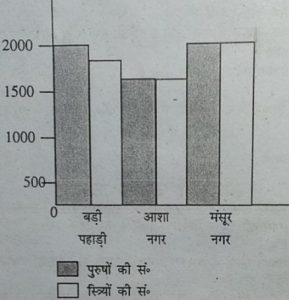
2. गाँव का नाम बड़ी पहाड़ी आशा नगर मंसूर नगर
पुरुषों की सं. 2000 1500 1500
स्त्रियों की सं. 1800 1500 2000
3. विषय हिन्दी अंग्रेजी गणित विज्ञान सामाजिक विज्ञान
हेतु द्वारा प्राप्त
अंक 50 40 80 70 48

4. टीन चैंपियन ट्राफी में वर्ल्ड कप 2007 में पिछले
2006 तक 10 ODI
द. अफ्रीका 75% 78%
आ. 61% 40%
श्रीलंका 54% 38%
न्यूजीलैंड 47% 50%
इंग्लैण्ड 46% 50%
पाकिस्तान 45% 44%
वेस्टइंडीज 44% 30%
भारत 43% 56%

आँकड़ों का वर्गीकरण—इकट्ठे किए गए अवलोकनों के समूह को यथा प्राप्त आंँकड़े कहते हैं।
परिसर–अधिकतम प्राप्तांक तथा न्यूनतम प्राप्तांक के अंतर को परिसर कहते हैं। कौन-सा
अंक कितनी बार आया है यह उसकी बारंबारता कहलाती है तथा हम इसे मिलान चिह्नों से दर्शाते हैं।
किसी प्रविष्टि की बारंबारता वह संख्या है जितनी बार वह प्रविष्टि आंकड़ों में आती है।
हम अपनी सुविधा के अनुसार प्रेक्षणों के कुछ समूह या वर्ग बनाते हैं जिससे विविधता भरे
आँकड़ों की परेशानी से बच जाते हैं। इसे बारंबारता बंटन सारणी कहते हैं। जब आंकड़ों को
इस प्रकार लिखा जाता है तो वे वर्गीकृत आँकड़े कहते हैं।
इससे अर्थपूर्ण निष्कर्ष निकालने में सहायक होती है।
दंडालेखों में वर्ग अंतराल की ऊंँचाई से उस वर्ग अंतराल को बारंबारता का पता चलता है।
स्वयं करके देखिए :
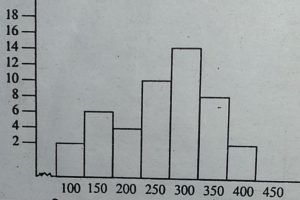
(अ) इस आयत चित्र द्वारा क्या सूचना दी जा रही है?
उत्तर–इस आयत चित्र द्वारा छात्रों द्वारा पुस्तकों पर किए गए खर्च की जानकारी
दी जा रही है।
(ब) किस वर्ग में अधिकतम छात्र है?
उत्तर–300–350 के वर्ग में अधिकतम छात्र है।
(स) कितने छात्रों का खर्च 300 या उससे अधिक है?
उत्तर-14।
(द) वर्ग साइज क्या है?
उत्तर-150–100 = 50।
(य) क्या इस आरेख से 100 से खर्च वाले छात्र की संख्या का पता चलता है ?
उत्तर–नहीं।
प्रश्नावली-4.1
1. अवकाश के दिनों में कक्षा–8 के विद्यार्थियों द्वारा प्रतिदिन पढ़ने के समय (घंटों में),
दिए हुए आलेख में दर्शाए गए हैं :
उत्तर–
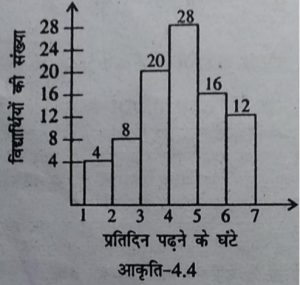
निम्नलिखित प्रश्नों के उत्तर दीजिए :
(अ) अधिकतम विद्यार्थियों ने कितने घंटों तक पढ़ा ?
(ब) 5 घंटों से कम समय तक कितने विद्यार्थियों ने पढ़ा ?
(स) कुल कितने विद्यार्थियों ने अवकाश के दिनों में भी पढ़ा ?
(द) किस वर्ग अन्तराल की बारम्बारता अधिकतम है ?
उत्तर-(अ) 4–5 घंटे।
(ब) 4+8+20+28 = 60 विद्यार्थी ।
(स) 4+8+20+28+16+ 12 = 88 विद्यार्थी ।
(द) 4–5 ।
2. अपनी कक्षा के सभी छात्रों के जूते या चप्पलों के माप एकत्रित कीजिए। उन्हें निम्न
तालिका में भरकर एक बारम्बारता बंटन सारणी बनाइए।
जूतों की माप मिलान चिह्न बारम्बारता
5 नम्बर
6 नम्बर
7 नम्बर
8 नम्बर
उत्तर–

3. ककड़िया गाँव के 27 मकानों के एक माह का बिजली बिल रुपयों में निम्नलिखित
324, 700, 617, 400, 356, 365, 435, 548, 780, 570, 312, 584, 506,736,
378, 685, 630, 674, 754,776, 596, 745, 763,422,580, 565, 570
वर्ग अन्तराल 300–400 आदि लेकर एक बारम्बारता सारणी बनाइए।
उत्तर–

4. प्रश्न-3 में दिए आँकड़ों से प्राप्त सारणी के लिए एक आयत चित्र बनाइए और
निम्नलिखित प्रश्नों के उत्तर दीजिए-
(i) किस समूह में बिजली उपभोक्ता की संख्या सबसे अधिक है।
(ii) कितने बिजली उपभोक्ता 500 रुपये या उससे अधिक बिल जमा करते हैं।
(iii) कितने उपभोक्ता 400 रुपये से कम का बिल जमा करते हैं?
(iv) वर्ग अन्तराल 400–500 की उच्च सीमा एवं निम्न सीमा क्या है?
(v) आलेख में कितने वर्ग अन्तराल है ?
उत्तर-

(i) 500–6001 (ii) 8+4+7= 19 । (iii) 5+3= 8 । (iv) उच्च सीमा = 500,
निम्न सीमा =400 । (v) 5 ।
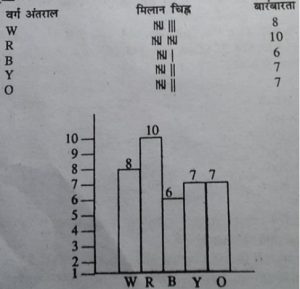
5. राजू अपने घर के कपड़ों को रंगों के आधार पर अलग करके इस प्रकार अंकित करता
है–उजला (W) लाल (R) काला (B) पीला (Y) अन्य रंग (O) । बनाई गई सूची निन
रूप में है–
R R O W R B Y R B W W O O R B Y Y O W R B Y Y B R R O W W R W O O R Y W B Y
मिलान चिह्नों का प्रयोग करते हुए एक बारम्बारता बंटन सारणी बनाइए । इसे प्रदर्शित
करने के लिए एक दंड आलेख खींचिए।
उत्तर–
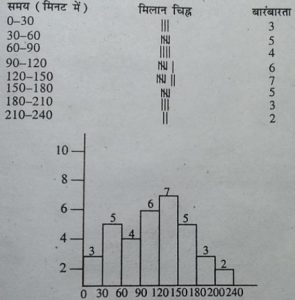
6. अपनी कक्षा के छात्रों से यह जानकारी प्राप्त कीजिए कि वह घर पर पिछले दिन
कितने समय पढ़े । इन आँकड़ों को निम्न वर्गीकृत बारम्बारता सारणी भरिए।
समय (मिनट में) मिलान चिह्न बारम्बारता
0–30
30–60
60–90
90–120
120–150
180–210
210–240
उपरोक्त आँकड़ों का एक आयत चित्र बनाइए।
उत्तर–
7. निम्नलिखित में से किस प्रकार के आँकड़ों को दर्शाने के लिए आप एक आयत चित्र
का प्रयोग करेंगे?
(अ) घर के विभिन्न अनाजों की मात्रा।
(ब) किसी विद्यालय के सभी विद्यार्थियों की ऊँचाई।
(स) 5 कंपनियों द्वारा निर्मित टेलीविजनों की संख्या।
(द) एक व्यस्त चौराहे पर प्रात: 8.00 बजे से दोपहर 2 बजे तक गुजरने वाली वाहनों
की संख्या।
(य) आपके वर्ग के सभी छात्रों का घर से विद्यालय की दूरी । (मीटर में) प्रत्येक
के लिए कारण भी दीजिए।
उत्तर–अ, ब तथा य को वर्ग अन्तरालों में दर्शाया जा सकता है तथा आयत चित्र खींचा जा सकता है।
वृत्त आलख या पाइ चाट
किसी वृत्त के केन्द्र पर बने कोणों का योग 360° होता है। जब सम्पूर्ण वृत्त को त्रिज्यखंडों
में विभाजित किया जाता है तथा प्रत्येक त्रिज्या का आकार उसके द्वारा निरूपित सूचना के
समानुपाती होता है तो इस प्रकार के निरूपण को वृत्त आलेख कहते हैं।
उदाहरण–
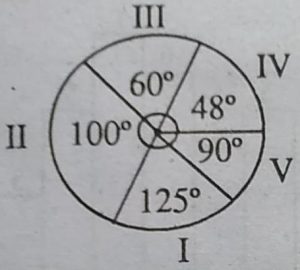
एक दिन में विद्यालय में छात्रों की उपस्थिति
वर्ग l II III IV V
छात्रों की सं. 15 60 36 27 18
हल:
वर्ग छात्रों की सं. केन्द्रीय कोण
I 75 75/216×360 = 125°
II 60 60/216×360 =100°
lll 36 36/216×360 = 60°
lV 27 27/216×360 = 45°
V 18 18/216×360 = 30°
216
प्रश्नावली-4.2
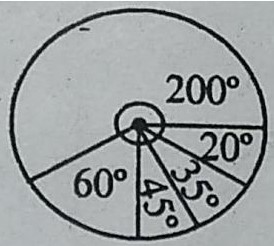
1. किसी विद्यार्थी के छोटी-सी पुस्तकालय में विभिन्न विषयों की पुस्तकें नीचे दी गई
हैं। इन आंकड़ों को एक पाई चार्ट द्वारा प्रदर्शित कीजिए।
विषय विज्ञान गणित अंग्रेजी हिन्दी सा. अध्ययन योग
पुस्तकें 40 12 9 7 4 72
उत्तर-
वर्ग छात्रों की सं. केन्द्रीय कोण
विज्ञान 40 200°
गणित 12 60°
अंग्रेजी 9 45°
हिन्दी 7 35°
सा. अध्ययन 4 20°
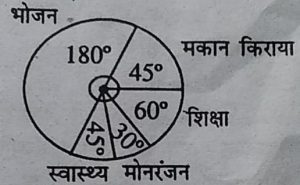
2. एक परिवार की मासिक आय 12000 रु. है। परिवार की मासिक खर्च निम्नानुसार
है, दिए गये आंकड़ों से पाई चार्ट बनाइए।
मद मकान किराया भोजन शिक्षा मनोरंजन स्वास्थ्य
खर्च (रु. में) 1500 6000 2000 1000 1500
उत्तर-
मकान किराया 1500 27°
भोजन 6000 108°
शिक्षा 2000 36°
मनोरंजन 1000 18°
स्वास्थ्य 1500 45°
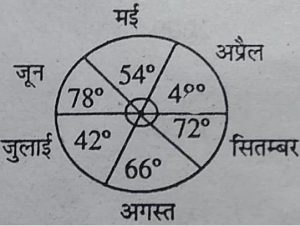
3. विभूति द्वारा गणित की छः माहों की मासिक जांच परीक्षा के प्राप्तांक निम्नानुसार है-
महीनों के नाम अप्रैल मई जून जुलाई अगस्त सितम्बर
प्राप्तांक 100 में 40 45 65 35 55 60
उपरोक्त आंकड़ों से पाई चार्ट बनाइए।
उत्तर-
महीनों के नाम प्राप्तांक केन्द्रीय कोण
अप्रैल 40 48°
मई 45 54°
जून 65 78°
जुलाई 35 42°
अगस्त 55 66°
सितम्बर 60 72°
4. एक विद्यालय के कक्षा 1 से V तक के 900 विद्यार्थियों की संख्या लेखाचित्रानुसार
है। लेखाचित्र की सहायता से बताइए-
(i) कक्षा-I में कुल कितने विद्यार्थी हैं ?
(ii) सबसे कम विद्यार्थी किस कक्षा में हैं ?
(iii) कक्षा-III से कक्षा-V तक कुल कितने विद्यार्थी हैं ?
उत्तर-संयोग और प्रायिकता—अब हम ऐसी परिस्थितियों का सामना करते हैं जहाँ
परिणाम की संभावना अप्रत्याशित अर्थात् निश्चित न हो तो इसे संयोग कहते हैं।
सम संभावित परिणाम (Equaly likely)–जब सभी में से प्रयोग के विभिन्न परिणाम
आने की संभावना बराबर हो तो इसे सम संभावित परिणाम कहते हैं। जैसे यदि एक सिक्का
उछाला जाए तो चित तथा पट दोनों के आने की संभावना बराबर होती है।
प्रायिकता (Probability)-जब हम एक सिक्का उछालते हैं तो यहाँ चित प्राप्त करने
की संभावना 2 परिणामों में से एक है अर्थात् ½ है, यहाँ चित प्राप्त करने की प्रायिकता =½
है।
प्रश्नावली-4.3
1. दो सिक्कों को एक साथ उछाला जाता है। एक सिक्के के चित आने की क्या
प्रायिकता है?
उत्तर–दो सिक्कों को एक साथ उछाला जाता है।
.: सिक्कों की सं० =2
संभावना =1
.: प्रायिकता = ½
2. एक थैले में 6 सफेद, 11 लाल और 7 पीले रंग की गेंद हैं । उस थैले में से एक पीले
गेंद निकालने की प्रायिकता ज्ञात कीजिए।
उत्तर–कुछ संभावनाएँ = 6 + 11+7= 24
पीले रंग की गेंदे =7
.: प्रायिकता = 7/24
3. अच्छी तरह से फेटी हुई 52 ताशों की एक गड्डी में से 1 इक्का प्राप्त करने की
प्रायिकता क्या होगी?
उत्तर–ताश की गड्डी के ताशों की संख्या = 52
इक्कों की सं० =4
प्रायिकता = 4/52 = 1/13
4. जब एक पासे को फेंका जाता है तब निम्नलिखित प्रत्येक घटना से प्राप्त होने वाले
प्रायिकताओं को लिखिए :
(i) (a) एक अभाज्य संख्या
(b) एक अभाज्य संख्या नहीं
(ii) (a) 4 से बड़ी एक संख्या
(b) 4 से बड़ी संख्या नहीं
(iiii) एक सम संख्या
उत्तर-(i) (a) पासे को फेंकते वक्त आने वाले अंकों की संभावना
= 1, 2, 3, 4, 5, 6 = 6
प्रायिकता = 2/6 = 1/3
(b) एक अभाज्य सं० छोड़ने पर संभावनाएँ = 5
.: प्रायिकता = 5/6
(iii) (a) 4 से बड़ी सं० = 5,6=2
.: प्रायिकता = 2/6 = 1/3
(b) 4 से बड़ी नहीं अर्थात् छोटी सं० = 1, 2, 3 = 3
प्रायिकता = 3/6 = 1/2
(iii) सम सं० = 2,4,6=3
प्रायिकता = 3/6 = 1/2
5. 12 अलग-अलग पर्चियों पर 1 से 12 तक संख्याएँ लिखी हुई हैं (एक पर्ची पर एक
संख्या) उन्हें एक डब्बे में रखकर अच्छी तरह मिला दिया जाता है । डब्बे के अन्दर
से बिना देखे एक पर्ची निकाली जाती है। निम्नलिखित की प्रायिकता क्या होगी–
(i) संख्या 5 प्राप्त करना (ii) संख्या 13 प्राप्त करना
(iii) संख्या 1 से 12 में कोई एक प्राप्त करना।
उत्तर–1 से 12 तक की सं० = 12
(i) संख्या 5 प्राप्त करने की प्रायिकता = 1/12
(ii) संख्या 13 प्राप्त करने की प्रायिकता = 1/12
(ii) सं. 1 से 12 में से कोई एक सं० प्राप्त करने की प्रायिकता = 12/12 = 1
◆◆◆
