BIHAR BOARD CLASS 8TH MATH | परिमेय संख्याएँ
BIHAR BOARD CLASS 8TH MATH | परिमेय संख्याएँ
परिमेय संख्याएँ
अज्ञात व चर की राशि के अलग-अलग समूहों को समीकरण कहते हैं।
जैसे–x+5=8
x = 8–5
x=3
यहाँ अज्ञात मान x, 3 मान से संतुष्ट होता है तथा 3 एक प्राकृत संख्या है।
दूसरा उदाहरण-
x + 15 = 7
x=7–15
x=–8x
यहाँ x का मान (-8) है जो कि एक ऋणात्मक पूर्ण संख्या है।
कुछ और समीकरणों को देखते हैं-
(i) 4x=5
x=5/4
यहाँ x का मान 5/4 है।
(ii) 5x+8=0
5x=0–8
5x=–8
x= –8/5
यहाँ 5/4 तथा –8/5 एक परिमेय संख्याएँ हैं।
संख्याओं के गुण धर्म―
(i) संवृत्त (संवरक नियम)-जब दो पूर्ण संख्याओं को आपस में जोड़ा जाता है तो उनका
योगफल एक पूर्णाक होता है।
अर्थात् a + b = पूर्ण संख्या
जहाँ a = पूर्ण संख्या
b= पूर्ण संख्या
(ii) व्यवकलन-जब एक पूर्ण संख्या में से किसी दूसरी पूर्ण संख्या को घटाया जात है
तो ऋणात्मक पूर्ण संख्या प्राप्त होती है।
अर्थात् a–b = ऋणात्मक पूर्ण संख्या
जहाँ a तथा b एक पूर्ण संख्या है तथा a <b
उदाहरण के तौर पर 6–4= 2, जहाँ a >b
4–5 = –1
जहाँ a<b
(iii) गुणन-जब एक पूर्ण संख्या को किसी दूसरी पूर्ण संख्या से गुणा करते हैं तो
गुणनफल भी एक पूर्ण संख्या होता है।
अर्थात् a×b = ab
3×5 = 15 (पूर्ण संख्या)
(iv) भाग-एक पूर्ण संख्या को किसी दूसरी संख्या से भाग देने पर सदैव एक पूर्ण संख्या
प्राप्त नहीं होती।
जैसे–4÷2 = 2 (पूर्ण संख्या)
4÷3= 4/3
पूर्णांक : योग– –8+3= -5
8 + 3 = 11
अतः पूर्णांक योग के अंतर्गत संवृत है।
व्यवकलन :
12–7= 5 पूर्णाक है
9–12 = –5 पूर्णाक है।
गुणन-किसी भी पूर्णांकों का गुणनफल भी एक पूर्णांक होता है।
जैसे– 5×18=90
–4×3=–12
भाग-किसी पूर्णांक को पूर्णांक से भाग देने पर भागफल भी पूर्णांक हो यह आवश्यक नहीं
होता है।
जैसे- 12÷3= 4 (पूर्णांक)
4÷5 = 4/5 (पूर्णांक नहीं है)
परिमेय संख्याएँ–ऐसी संख्या जो p/q के रूप में व्यक्त की जा सके। परिमेय संख्याएँ
कहलाती हैं । यह p तथा q पूर्णाक है तथा 4 ≠ 0 है जैसे–
–0,–5,3/5,–7/12
परिमेय संख्या योग के गुणधर्म के अंतर्गत संवृत्त है।
जैसे– –4/5+ (–3/10)=–8+(–3)/10 = –11/10 (परिमेय संख्या)
व्यवकलन―परिमेय संख्याएँ व्यवकलन के अन्तर्गत संवृत्त है। अर्थात् दो परिमेय संख्याओं
a तथा b के लिए a–b भी एक परिमेय संख्या है।
8/9 – 5/6= 16–5/6 = 11/6 (परिमेय संख्या)
गुणन—दो परिमेय संख्याओं का गुणनफल भी एक परिमेय संख्या है।
–4/5×8/9= –32/15 (परिमेय संख्या है।
भाग–दो परिमेय संख्याओं का भागफल भी परिमेय संख्या होती है।
–5/4÷ 5/3= 25/12 (परिमेय संख्या)
स्वयं करके देखिये-
संख्याएँ संवृत्त है
योग के व्यकलन के गुणन के भाग के
परिमेय सं हाँ हाँ हाँ हाँ
पूर्णांक सं. हाँ नहीं हाँ हाँ
पूर्ण सं. हाँ हाँ हाँ नहीं
प्राकृत सं. हाँ नहीं नहीं हाँ
क्रम विनिमेयता (Commutative law)
योग–दो पूर्ण संख्याओं a तथा b के लिए a + b = b + a सत्य होता है।
जैसे- माना कि a= 5, b =4
a+b=b+a
5+4 = 4 + 5
9=9
व्यवकलन—दो पूर्ण संख्याओं a तथा b के लिये व्यवकलन का क्रम विनिमेय नियम सत्य
नहीं है।
अर्थात् दो पूर्ण संख्याओं के लिए a–b≠b–a
जैसे– 8–2= 6
2–8= –6
गुणा–दो पूर्ण संख्याओं के लिए गुणन का क्रम विनिमेय नियम सत्य होता है।
अर्थात् a×b = b×a
जैसे 5×3=3×5
15 = 15
भाग-दो परिमेय संख्याओं के लिए a÷b = b÷a सत्य नहीं होता है।
जैसे–4÷2= 2
2÷4= 1/2
पूर्णांक :
(अ) योग-पूर्णांकों के लिए योग का क्रम विनिमेय नियम सत्य होता है।
(i) (–5)+(+4) = –2
(ii) +4 + (–5) = –1
(iii) 5+ (–4)=1
(iv) (–4)+5=1
व्यवकलन–दो पूर्णांक संख्याओं के लिए क्रम विनिमेय का नियम सत्य नहीं होता अर्थात्
a – b ≠ b – a
जैसे– (i) –8 – (+3)= –11
(ii) 3 –(–8)= 3 + 8 = 11
गुण–दो पूर्णांक संख्याओं के लिए गुणन का क्रम विनिमेय नियम सत्य है अर्थात्
a×b=b×a
जैसे 3×5= 15
5×3=15
भाग–दो पूर्णांक संख्याओं के लिए भाग का क्रम विनिमेय नियम सत्य नहीं होता है।
अर्थात्– a÷b≠b÷a
जैसे– –5÷ (+2)= –5/2
+2÷ (–5) = – 2/5
और –5/2≠(–2/5)
निम्नलिखित सारणी को क्रम विनिमेयता नियम के लिए पूरा कीजिए-
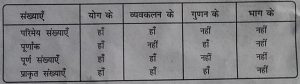
साहचर्यता (सहचारिता)
योग–तीन पूर्ण संख्याओं के लिए योग का साहचर्यता नियम सत्य होता है।
अर्थात् तीन पूर्ण संख्याओं a, b तथा c के लिए-
(a+b) + c=a+(b+ c) होता है।
जैसे–(4+5)+6=4+ (5+6)
9+ 6 = 4 + 11
15 = 15
व्यवकलन–तीन पूर्ण संख्याओं के लिए व्यवकलन (घटाव) की साहचर्यता का नियम सत्य
नहीं होता है।
अर्थात् (a–b)–c≠a–(b–c)
जैसे (5–4)–3≠5–(4–3)
r–3≠5–1
–2≠4
गुणन–तीन पूर्ण संख्याओं a, b तथा c के लिए (a×b)xc=a× (b×c) सत्य होता है ।
जैसे—(5×4)×3=5× (4×3)
20×3=5×12
60 = 60
भाग–तीन पूर्ण संख्याओं a, b तथा c के लिए साहचर्यता का नियम सत्य नहीं होता।
जैसे–(4÷5)÷6≠4 (5÷6)
4/5×1/6≠1/4×5/6
4/30≠5/24
पूर्णाक–तीन पूर्णाक (–5), 4 तथा (–2) के लिए साहचर्यता के नियम-
योग– (a+b)+c=a+(b+c)
(–5+4)+(–2)=–5+ {4–(–2)}
–1 –2 =–5+ (4–2)
–3 = –5+2
(–3)=(–3)
आकलन (घटाव)– –5, –4 तथा –6 के लिए-
(–5–4)–(–6) = –9 +6 = –3
–5–{(4–(–6)} = –5 – (4 + 6) = –5 –10=–15
गुणन―
(–5×–4)×6)=–5×(–4×(–6))
–20×(–6)=–5×(–24)
–120 = –120
भाग–
(–5÷(–4))=(–6)=–5÷(4÷(–6))
–5/–4×1/–6=1/–5×(–4)/–6
–5/–24≠(–4)/30
परिमेय संख्याएँ–
योग–
(–5/4+3/8)+(–7)/6=–5/4+(3/8+(–
(–10+3/8)+(–7)/6=–5/4+(9–28/
=–7/8+(–7)/6=–5/4+(–19)/24=–
–30–19/24=–49/24=–49/24
व्यकलन (घटाव)―
(–3/8–5/4) – (–2/6) = –3/8 – (5/4 – (–2)/6)
(–3 –10/8) – (–2/6) = –3/8 – (15+4/12)
–13/8 – (–2)/6 = –3/8 – 19/12
–39–(–8)/24 = –9–38/24
= –31/24 ≠ –47/24
अतः परिमेय संख्याओं के लिए व्यवकलन की साहचर्यता का नियम सत्य नहीं है।
गुणन–
= (–5/8×7/6)×(–2)/5 = –5/8×(7/6×(–2)/5)
= –35/48×(–2)/5 = –5/8×(–14)/30
= 70/240 = 70/240
अतः परिमेय संख्याओं के लिए (a×b)×c = a × (b×c)
भाग–
(1/2÷3/4)÷(–5)/8 1/2÷(3/4÷(–5/8))
= (1/2×4/3)÷(–5/8)) 1/2÷(3/4×8/–5)
4/6×8/–5 2/1×24/–20
.: 32/–30≠48/–20
अतः परिमेय संख्याओं के लिए भाग का नियम सत्य नहीं है।
शून्य : (0)
किसी पूर्ण संख्या, पूर्णाक तथा परिमेय संख्या में जब शून्य जोड़ा जाता है तो योगफल फिर
से वही संख्या प्राप्त होता है। इसलिए शून्य एक भोज्य तत्समक कहलाता है।
एक: (1)
जब किसी पूर्ण संख्या, पूर्णांक तथा परिमेय संख्या में जब 1 से गुणा किया जाता है तो
गुणनफल फिर से वही प्राप्त होता है। अत: (1) एक गुणात्मक तत्समक है।
योज्य प्रतिलोम–जब दो संख्याओं का योग शून्य हो तो ये दोनों संख्याएँ एक-दूसरे का
योज्य प्रतिलोम कहलाते हैं।
जैसे– –2 का योज्य प्रतिलोम है+2।
व्युत्क्रम अथवा गुणात्मक प्रतिलोम–जब दो संख्याओं का गुणनफल 1 हो तो वे दोनों
संख्याएँ एक-दूसरे की व्युत्क्रम अथवा गुणात्मक प्रतिलोम कहलाती है।
जैसे― 3/5×b/a=1
सभी परिमेय संख्याओं a,b एवं c के लिए
a× (b+c) = (a×b)+ (a×c)
a× (b–c) = (a ×b)–(a×c)
स्वयं करके देखिए-
(i) (5/4×(–2/8)+(5/4×(–3/5))
⇨(5/4×(–2/8)+(5/4×(–3/5))
⇨(10/32+15/20) = 5/16+3/4
= –5/16+(–3/4)= –5–12/16= –17/16
(ii) 5/8×(–3/7+(–7)/6)
= (5/8×(–3)/7)+(5/8×(–7)/6)
= –15/56+(–35)/48 = –90–245/336 = –335/336
प्रश्नावली-1.1
1. निम्नलिखित में से प्रत्येक के योग्य प्रतिलोम लिखिए :
(i) 2/3 (ii) 25/9 (iii) –16 (iv) –15/8
(v) 0 (vi) –5/–7 (vii) 13/–5 (viii) –2/15
उत्तर― (i) –2/3 (ii) –25/9 (iii) +16 (iv) –15/8
(v) 0 (vi) –5/–7 (vii) 13/–5 (viii) 2/15
2. नम्नलिखित सारणी के खाली स्थान को भरिए :
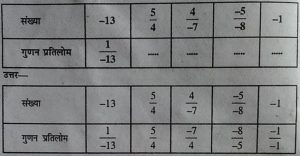
3. उचित गुण धर्मों के उपयोग से निम्नलिखित का मान ज्ञात कीजिए―
(i) 4/3+3/5+(–2/3)+(–11)/5
उत्तर― (4/3+3/5)+(–2/3+(–11)/5)
= (20+9/15)+(–10–33/15)
= 29/15+(–43/15)= 29–43/15= –14/15
(ii) 2/5×(–3/7)-1/6×3/2+1/14×2/5
उत्तर― (2/5×3/7)–(1/6×3/2)+(1/7×2/5)
= –6/35–1/4+1/35
= (–6/35+1/35)–1/4=–5/35–1/4= –20–35/140
= –55/140 = –11/28
4. 5/18 को –7/72 के व्युत्क्रम से गुणा कीजिए।
उत्तर― 5/18×72/7=20/–7
5. –1/3×(1/2+1/4)=(–1/3×1/2)+(–1/
उत्तर- साहचर्यता का वितरण नियम―
a× (b+c) = (a×b)+ (a×c)
6. क्या –1(1)/8 का गुणात्मक प्रतिलोम 8/9 है? कारण सहित उत्तर दीजिए।
उत्तर― 1(1)/8 = –9/8
गुणात्मक प्रतिलोम वह होता है जिससे किसी संख्या को गुणा किया जाए तो गुणनफल 1
होता है।
उत्तर― -9/8×8/9 = 1
.: 8/9 गुणात्मक प्रतिलोम है।
7. क्या 3(1)/3 का गुणात्मक प्रतिलोम 0.3 है ? क्यों अथवा क्यों नहीं?
उत्तर-3(1)/3 = 10/3
0.3 = 3/10
10/5×3/10 = 1
.: 3(1)/3 का गुणात्मक प्रतिलोम 0.3 है क्योंकि इन दोनों का गुणनफल 1 है।
8. निम्नलिखित को वितरण नियम की सहायता से हल कीजिए।
(i) –3/4×{2/3+(–5/6)} (ii) 5/6×(–2/5+3/10)
उत्तर― (i) –3/4×{2/3+(–5/6)} = –3/4×{2/3–5/6}
= –3/4×(6–5/6) = –3/4×1/6 = 3/24 = –1/8
(ii) 5/6×(–2/5+3/10)
= 5/6×(–4+3/10) = 5/6×(–1/10)
= 5/6×(–1)/10 = –1/12
9. निम्नलिखित कॉलम “अ” को कॉलम “ब” के उचित नियम से मिलाएँ-
उत्तर― कॉलम “अ” कॉलम “ब”
उदाहरण नियम
(i) (–1/2)+3/4=3/4+(–1/2) (j) योज्य तत्समक
(ii) 5/6×4/7=4/7×5/6 (i) गुणात्मक तत्समक
(iii) (–1/2+2/5)+3/10
= –1/2+(2/5+3/10) (h) गुणा का साहचर्य नियम
(iv) 1/4+3/8=5/8 (f) योज्य प्रतिलोम
(v) (5×1/2)×3/4=5×(1/2×3/4) (c) वितरण नियम
(vi) –5/4+0=–5/4 (a) संवरक नियम
(vii) –8/3×1= –8/3 (b) गुणात्मक प्रतिलोम
(viii) 5/2×(1/3+2/5)
=(5/2×1/3)+(5/2×2/5) (e) योग का साहचर्य नियम
(ix) 5/3×3/5 =1 (g) गुणा का क्रम विनिमेय नियम
(x) –7/4+7/4 = 0 (d) योग का क्रम विनिमेय नियम
◆◆◆

Question answer bahut lamba hai