bihar board class 10th maths | Some Applications of Trigonometry

Bihar Board Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry

प्रश्नावली 9.1

प्रश्न 1. सर्कस का एक कलाकार एक 20 m लम्बी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खम्भे के शिखर से बँधी हुई है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो, तो खम्भे की ऊँचाई ज्ञात कीजिए।
हल:

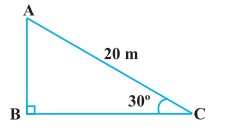
माना AB एक खम्भा है जिसका सिरा B भूमि पर गड़ा है।
खम्भे के शिखर A से एक तनी हुई डोरी AC भूमि पर एक स्थान (बिन्दु) C से बँधी है। डोरी AC की लम्बाई 20 m है।
डोरी भूमि स्तर BC के साथ बिन्दु C पर ∠ACB = 30° बनाती है।
माना AB = h m
दिया है, AC = 20 m
समकोण ΔABC में,

अत: खम्भे की ऊँचाई 10 m है।

प्रश्न 2. आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30° का कोण बनाता है। पेड़ के पाद-बिन्दु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 m है। पेड़ की ऊँचाई ज्ञात कीजिए।
हल:

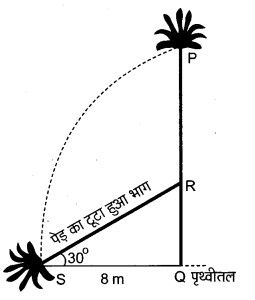
माना PQ एक पेड़ है जो बिन्दु R से टूटकर भूमि पर गिर गया है।
पेड़ के ऊपरी भाग RP का ऊपरी सिरा P भूमि पर बिन्दु S को छू रहा है।
बिन्दु S की पेड़ से दूरी SQ = 8 m है।
पेड़ का टूटा हुआ भाग PR, भूमि पर बिन्दु S से ∠QSR = 30° बनाता है।
तब, समकोण ΔQSR में,

प्रश्न 3. एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5 m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3 m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लम्बाई क्या होनी चाहिए?
हल: जब ठेकेदार 5 वर्ष से कम उम्र के बच्चों के लिए फिसलनपट्टी लगाता है तो उसकी ऊँचाई AB = 1.5 m तथा फिसलनपट्टी का भूमि के साथ कोण ∠ACB = 30° है।
माना इस स्थिति में फिसलनपट्टी की लम्बाई AC m है।

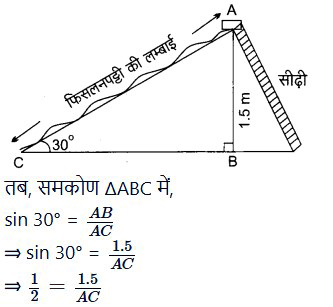
⇒ AC = 2 × 1.5 = 3 m
⇒ AC = 3 m
जब ठेकेदार 5 वर्ष से अधिक उम्र के बच्चों के लिए फिसलनपट्टी लगाता है, तो उसकी ऊँचाई A’B’ = 3 m होती है और फिसलनपट्टी भूमि के साथ कोण ∠A’C’B’ = 60° बनाती है।
माना इस स्थिति में फिसलनपट्टी की लम्बाई A’C’ m है।

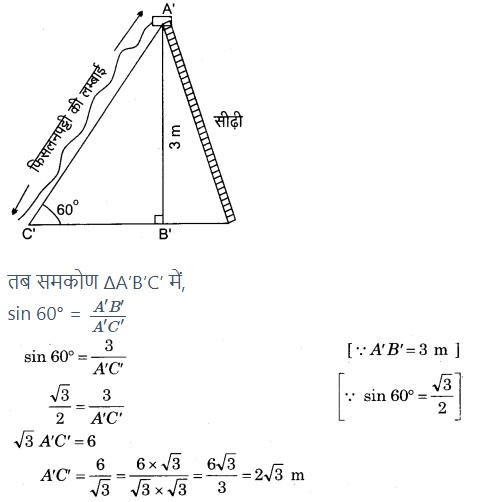
अत: 5 वर्ष से कम उम्र के बच्चों के लिए फिसलनपट्टी की लम्बाई = 3 m तथा इससे अधिक उम्र के बच्चों के लिए फिसलनपट्टी की लम्बाई = 2√3 m

प्रश्न 4. भूमि के एक बिन्दु से जो मीनार के पाद-बिन्दु से 30 m की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए। (√3 = 1.73)
हल: मान लिया, भूमि तल पर एक मीनार AB है जिसकी चोटी (शिखर) A तथा आधार (नीव) B है। मीनार के आधार Bसे 30 m दूर भूमि पर स्थित कोई बिन्दु C है। बिन्दु C से मीनार के शिखर A का उन्नयन कोण ∠ACB = 30° है।
माना मीनार AB की ऊँचाई h m है।

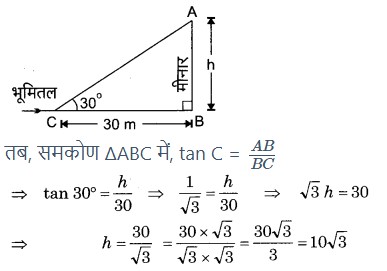
अत: मीनार AB की ऊँचाई = 10√3 m = 10 × 1.73 = 17.3 m

प्रश्न 5. भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिन्दु से बाँध दिया गया और भूमि के साथ डोरी का झकाव 60° है। यह मानकर कि डोरी में कोई ढील नहीं है, डोरी की लम्बाई ज्ञात कीजिए।
हल: माना AX एक क्षैतिज रेखा है जिस पर स्थित एक बिन्दु C से BC = 60 m की ऊँचाई पर एक पतंग B उड़ रही है।
यह पतंग B, क्षैतिज भूमि पर स्थित एक बिन्दु A से तनी हुई डोरी AB द्वारा संयोजित है।
डोरी AB का भूमि के साथ कोण (झुकाव) 60° है।

अत: डोरी की लम्बाई 40√3 या 69.2 m है। (उन्नयन कोण)

प्रश्न 6. 1.5 m लम्बा एक लड़का 30 m ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है?
हल: माना PQ एक भवन है जिसकी ऊँचाई 30 m है। भवन के आधार से x m दूर बिन्दु R पर एक लड़का OR खड़ा है, जिसकी ऊँचाई OR = 1.5 m है।

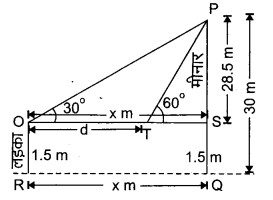
तब, OS || QR
∴ OR = SQ = 1.5 m
माना मीनार की चोटी P का लड़के की आँख O पर उन्नयन कोण ∠POS = 30° है।
तब, PS = PQ – SQ = 30 – 1.5 = 28.5 m

⇒ x = 28.5 × √3
⇒ x = 28.5 × 1.732 = 53.496 m
माना लड़का d दूरी चलकर बिन्दु T पर पहुँचता है जहाँ से उसकी आँख का कोण ∠PTS = 60° हो जाता है।
तब, समकोण ∆PTS में,

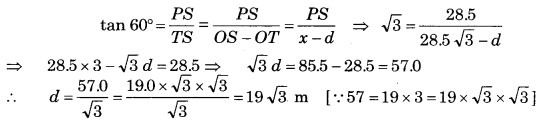
अत: लड़का भवन की ओर 19√3 m चलकर गया।

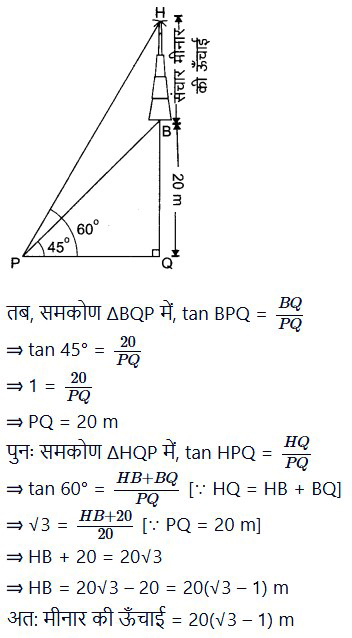
प्रश्न 7. भूमि के एक बिन्दु से एक 20 m ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः 45° और 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए।
हल: माना क्षैतिज भूमितल पर स्थित BQ एक भवन है जिसकी ऊँचाई BQ = 20 m है।
भवन की चोटी के ऊपर एक संचार मीनार BH स्थित है। भवन के आधार Q से किसी दूरी PQ पर एक बिन्दु P है।
बिन्दु P से संचार मीनार के तल का उन्नयन कोण ∠BPQ = 45° तथा शिखर H का उन्नयन कोण ∠HPQ = 60° है।
माना संचार मीनार की भूमि से ऊँचाई HQ है।

प्रश्न 8. एक पेडस्टल के शिखर पर एक 1.6 m ऊँची मूर्ति लगी है। भूमि के एक बिन्दु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी बिन्दु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
हल: माना PQ एक x m ऊँची पेडस्टल है जिसकी चोटी P पर एक मूर्ति PS लगी है। मूर्ति की ऊँचाई PS = 1.6 m है।
क्षैतिज भूमि पर स्थित एक बिन्दु R से मूर्ति के ऊपरी सिरे S का उन्नयन कोण ∠QRS = 60° है तथा इसी बिन्दु R से पेडस्टल के शिखर P का उन्नयन कोण ∠PRQ = 45° है।
मूर्ति PS की लम्बाई 1.6 m है।

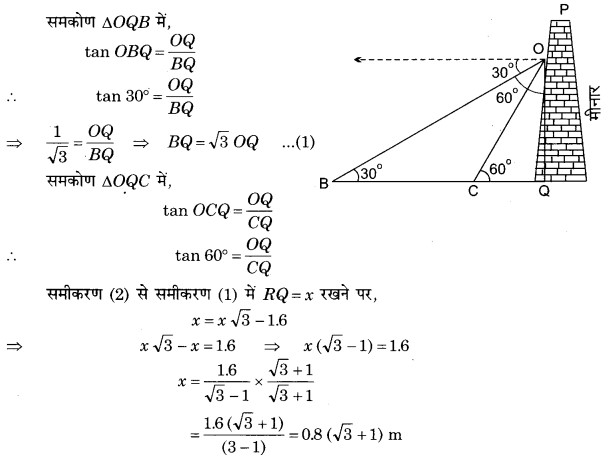
अत: मूर्ति की ऊँचाई 0.8(√3 + 1) m है।

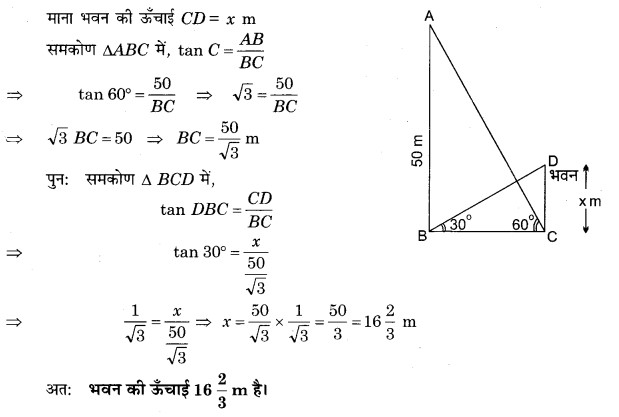
प्रश्न 9. एक मीनार के पाद-बिन्दु से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद-बिन्दु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50 m ऊँची हो, तो भवन की ऊँचाई ज्ञात कीजिए।
हल: माना AB एक मीनार है जिसकी ऊँचाई 50 m है। मीनार के पाद-बिन्दु B से एक भवन CD की चोटी D का उन्नयन कोण 30° है, जबकि भवन के आधार-बिन्दु C से मीनार की चोटी A का उन्नयन कोण 60° है। मीनार के आधार B से भवन के आधार C की दूरी BC है।
माना भवन की ऊँचाई CD = x m

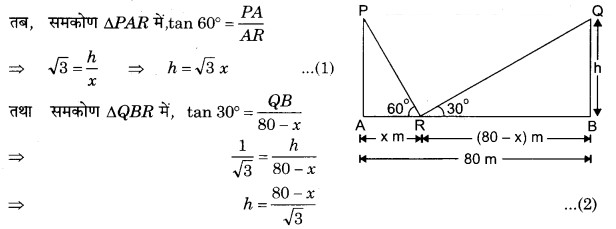
प्रश्न 10. एक 80 m चौड़ी सड़क के दोनों ओर आमने-सामने समान ऊँचाई वाले दो खम्भे लगे हुए हैं। इन दोनों खम्भों के बीच सड़क के एक बिन्दु से खम्भों के शिखर के उन्नयन कोण क्रमश: 60° और 30° हैं। खम्भों की ऊँचाई और खम्भों से बिन्द की दूरी ज्ञात कीजिए।
हल: माना, PA तथा QB समान ऊँचाई h m के दो खम्भे हैं जो सड़क की चौड़ाई AB के सिरों क्रमश: A व B पर स्थित हैं।
खम्भों की सीध में सड़क के किसी बिन्दु R से दोनों खम्भों के शिखर क्रमश: 60° व 30° के उन्नयन कोण बनाते हैं।
सड़क की चौड़ाई AB = 80 m तथा माना बिन्दु R की पहले खम्भे PA से दूरी x m है।
अत: बिन्दु R की खम्भे QB से दूरी = (80 – x) m

समीकरण (1) व (2) से,

⇒ 3x = 80 – x
⇒ 4x = 80 m
⇒ x = 20 m
समीकरण (1) में x का मान रखने पर,
h = √3 × 20 = 1.73 × 20 = 34.60 m
अतः खम्भे की ऊँचाई = 34.60 m और पहले खम्भे से प्रेक्षण बिन्दु की दूरी = 20 m
तथा दूसरे खम्भे से प्रेक्षण बिन्दु की दूरी = 80 – 20 = 60 m.

प्रश्न 11. एक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधरतः खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिन्दु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिन्दु से 20 m दूर और इस बिन्द को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिन्द से टॉवर के शिखर का उन्नयन कोण 30° है (चित्र देखिए)। टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।

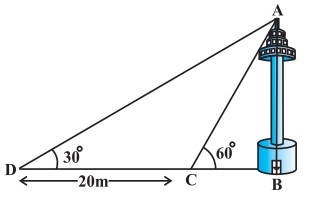
हल: माना BC चौड़ाई की एक नहर है जिसके एक तट B पर एक टीवी टॉवर AB खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक बिन्दु C से टॉवर के शिखर का उन्नयन कोण ∠ACB = 60° है। इसी तट पर इस बिन्दु से 20 m दूर तथा बिन्दु C और टॉवर के आधार B को मिलाने वाली रेखा की सीध में एक बिन्दु D है। बिन्दु D से टॉवर के शिखर का उन्नयन कोण 30° है।
माना टॉवर AB की ऊँचाई h m तथा नहर की चौड़ाई BC = x m है।
तब, समकोण ΔABC में,

समीकरण (1) में x का मान रखने पर, h = 10√3 m
अत: टीवी टॉवर की ऊँचाई = 10√3 m तथा नहर की चौड़ाई = 10 m

प्रश्न 12. 7 m ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
हल: माना AB एक केबल टॉवर है और उसी धरातल में एक भवन CD है जिसकी ऊँचाई 7 m है।
भवन के शिखर C से क्षैतिज धरातल के समान्तर एक रेखा CE है। भवन के शिखर C से केबल टॉवर के शिखर A का उन्नयन कोण ∠ACE = 60° है और केबल टॉवर के पाद B का अवनमन कोण ∠ECB = 45° है।

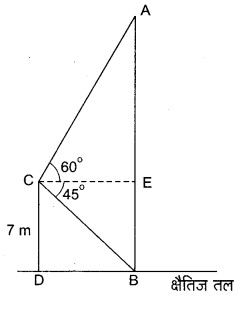
∵ DB || CE और ∠DCE = 90°
तथा ∠EBD = 90° ⇒ CD || EB
चतुर्भुज CDBE एक समान्तर चतुर्भुज है।
∴ EB = CD ⇒ EB = 7 m

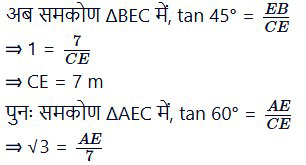
⇒ AE = 7√3 m
तब, केबल टॉवर AB की ऊँचाई = AE + EB = 7√3 + 7 = 7(√3 + 1) m
अत: केबल टॉवर की ऊँचाई 7(√3 + 1) m है।

प्रश्न 13. समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बीच की दूरी ज्ञात कीजिए।
हल: माना 75 m ऊँचे एक प्रकाश स्तम्भ PQ के शिखर P से, A और B जहाजों के अवनमन कोण क्रमश: 30° और 45° हैं।

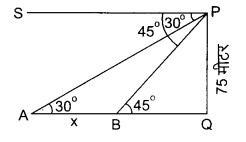
∴ ∠SPA = 30° = ∠PAQ (एकान्तर कोण)
तथा ∠SPB = 45° = ∠PBQ (एकान्तर कोण)
माना जहाजों के बीच की दूरी AB = x m
तब, समकोण ΔPQB में,

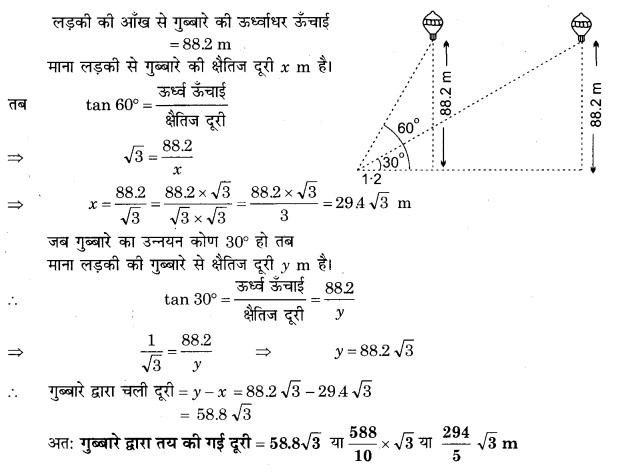
प्रश्न 14. 1.2 m लम्बी एक लड़की भूमि से 88.2 m की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° है। कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है। इस अन्तराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।

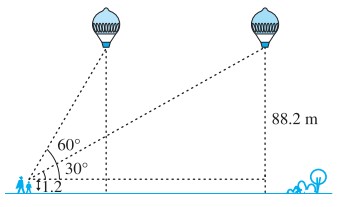
हल:

प्रश्न 15. एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एकसमान चाल से जाता है। छ: सेकण्ड बाद कार का अवनमन कोण 60° हो गया। इस बिन्दु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
हल: माना BCQ एक सीधा राजमार्ग है जिसके किसी बिन्दु Q पर खड़ी मीनार की ऊँचाई OQ है। एक प्रेक्षक मीनार के शिखर बिन्दु 0 पर बैठा देखता है कि एक कार B का अवनमन कोण 30° है जिससे ∠OBQ = 30° है। प्रेक्षक 6 सेकण्ड बाद देखता है कि कार का अवनमन कोण 60° है जिससे ∠OCQ = 60° है।
समकोण ∆OQB में,

अत: कार को मीनार के पाद तक पहुँचने में लगने वाला समय = 3 सेकण्ड

प्रश्न 16. मीनार के आधार से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो बिन्दुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए कि मीनार की ऊँचाई 6 m है।
हल: माना AB एक मीनार है जिसकी ऊँचाई h है। मीनार के आधार B के दोनों ओर B से क्रमश: 9 m और 4 m दूरियों पर दो बिन्दु P और Q स्थित हैं।
यदि बिन्दु P से मीनार की चोटी का उन्नयन कोण हो तो Q से मीनार की चोटी का उन्नयन कोण θ का कोटिपूरक (90° – θ) होगा।

त्रिकोणमिति के कुछ अनुप्रयोग Additional Questions

बहुविकल्पीय प्रश्न

प्रश्न 1.
जिस वक्त सूर्य का उन्नयन कोण 45° था, तब एक स्तम्भ की परछाई 10 m मापी गई। उस स्तम्भ की ऊँचाई थी
(i) 5 m
(ii) 10 m
(iii) 15 m
(iv) 20 m
हल
(ii) 10 m

प्रश्न 2.
10 m ऊँचे मकान के आधार से 10 m दूर स्थित बिन्दु से देखने पर उसकी छत का उन्नयन कोण होगा
(i) 60°
(ii) 45°
(iii) 30°
(iv) 75°
हल
(ii) 45°

प्रश्न 3.
यदि एक वृक्ष के आधार से 15 m दूर स्थित बिन्दु पर उसकी चोटी का उन्नयन कोण 30° बनता है, तो वृक्ष की ऊँचाई होगी।
(i) 15 m
(ii) 30 m
(iii) 15√3 m
(iv) 5√3 m
हल
(iv) 5√3 m

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
किसी समय कोई स्तम्भ की छाया की लम्बाई उसकी ऊँचाई की √3 गुनी है। सूर्य का उन्नयन कोण ज्ञात कीजिए।
हल
माना स्तम्भ AB की ऊँचाई h है, तब
छाया BC की लम्बाई = h√3
तथा उन्नयन कोण ∠ACB = θ

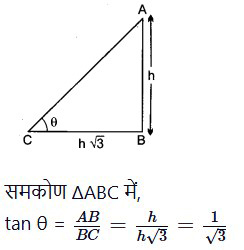
⇒ tan θ = tan 30°
⇒ θ = 30°
अत: सूर्य का उन्नयन कोण 30° है।

प्रश्न 2.
एक वृक्ष का ऊपरी भाग टूटकर भूमि से जा लगा तथा भूमि से 45° का कोण बनाता है। यदि वृक्ष की जड़ से उस बिन्दु जहाँ वृक्ष का शिखर भूमि को छूता है, की दूरी 6 m है, तो वृक्ष की ऊँचाई ज्ञात कीजिए।
हल
माना A वृक्ष ABC का पाद है तथा BC वृक्ष का टूटा हुआ भाग है तथा C पेड़ का ऊपरी सिरा है।
तब ∠ACB = 45°
तथा ∠BAC = 90°
प्रश्नानुसार, AC = 6 m

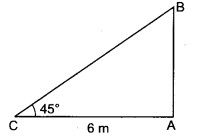
समकोण ∆BAC में, tan 45° = AB/AC
⇒ AB = AC tan 45° = 6 × 1 = 6 m
पुनः समकोण ∆BAC में, cos 45° = AC/BC
⇒ BC = AC sec 45° = 6√2
∴ पेड़ की कुल माप = AB + BC = 6 + 6√2 = 6(√2 + 1) m

प्रश्न 3.
एक मीनार की चोटी का उन्नयन कोण उस मीनार के आधार से क्षैतिज तल पर 40 m दूरी पर स्थित बिन्दु से देखने पर 45° है। मीनार की ऊँचाई ज्ञात कीजिए।
हल

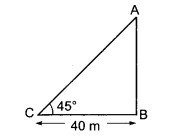
माना AB मीनार तथा बिन्दु C क्षैतिज तल पर मीनार के आधार से 40 m दूर स्थित बिन्दु है।
तब ∠ACB = 45°
समकोण ∆ABC में, tan 45° = AB/BC
⇒ 1 = AB/40
⇒ AB = 40 m
अत: मीनार की ऊँचाई 40 m है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
एक मीनार के आधार से एक सरल रेखा में 100 m तथा 150 m की दूरी पर स्थित दो बिन्दुओं से मीनार के शिखर का उन्नयन कोण पूरक कोण है। सिद्ध कीजिए कि मीनार की ऊँचाई 50√6 m है।
हल
AB एक मीनार है जिसकी ऊँचाई h m है। इसके आधार B से 100 m तथा 150 m दूरी पर दो बिन्दु C और D हैं जहाँ पर शिखर के उन्नयन कोण क्रमशः θ तथा (90° – θ) हैं।

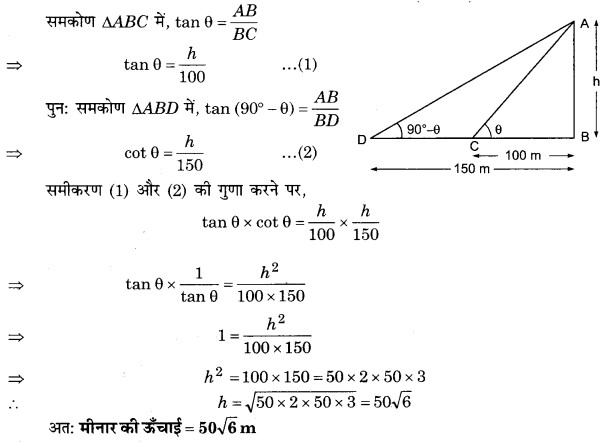
अत: मीनार की ऊँचाई = 50√6 m

प्रश्न 2.
भूमितल पर दो बिन्दु A तथा B किसी मीनार के एक ही ओर स्थित हैं। यदि A तथा B पर मीनार के शिखर के उन्नयन कोण क्रमश: 30° तथा 60° हैं। यदि मीनार की ऊँचाई 150 m है, तो A तथा B के मध्य दूरी ज्ञात कीजिए।
हल
माना PQ एक मीनार है जिसकी ऊँचाई 150 m है। मीनार के पाद Q से जाने वाली क्षैतिज रेखा पर दो बिन्दु A और B हैं, जहाँ से मीनार की चोटी P से उन्नयन कोण क्रमशः 30° तथा 60° हैं।

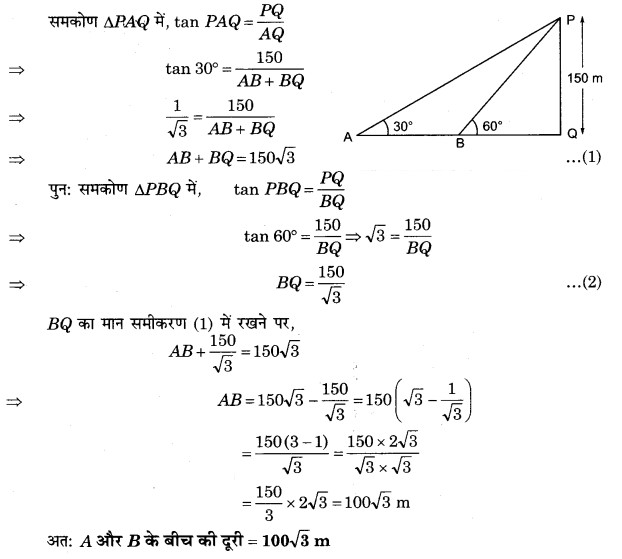
प्रश्न 3.
भूमि पर किसी बिन्दु से एक हवाई जहाज का उन्नयन कोण 60° है। 15 s की उड़ान के पश्चात् उन्नयन कोण बदलकर 30° हो जाता है। यदि हवाई जहाज 1500√3 m की नियत ऊँचाई पर उड़ रहा है, तो हवाई जहाज की चाल किमी प्रति घण्टा में ज्ञात कीजिए।
हल
माना हवाई जहाज 15 सेकण्ड में C से D तक पहुँच जाता है।
समकोण ∆ABC में,

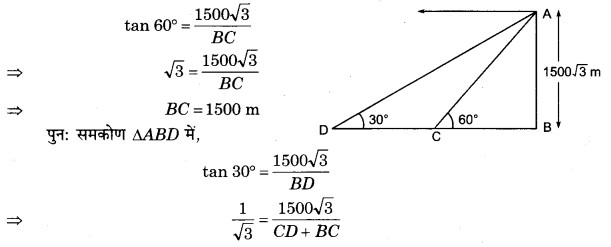
⇒ CD + BC = 1500√3 × √3 = 4500
⇒ CD + 1500 = 4500 [∵ BC = 1500 m]
⇒ CD = 4500 – 1500 = 3000 m
प्रश्नानुसार, हवाई जहाज को 3000 m जाने में 15 s लगते हैं।

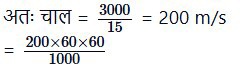
= 720 km/h
अतः हवाई जहाज की चाल = 720 km/h

प्रश्न 4.
एक नदी के पुल के एक बिन्दु से नदी के सम्मुख किनारों के अवनमन कोण क्रमशः 30° और 45° हैं। यदि पुल किनारों से 3 m की ऊँचाई पर हो तो नदी की चौड़ाई ज्ञात कीजिए।
हल
माना PQ नदी की चौड़ाई है। माना A नदी के पुल का एक बिन्दु है अर्थात् AB = 3 m
A से नदी के सम्मुख किनारों P और Q अवनमन कोण क्रमश: 30° और 45° हैं।

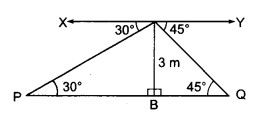
समकोण ∆ABQ में,

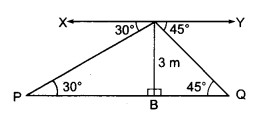
⇒ BP = 3√3 m
अतः नदी की चौड़ाई = PQ = BP + BQ
= (3√3 + 3) m
= 3(√3 + 1) m
= 3(1.732 + 1) m
= 3(2.732) m
= 8.196 m
≅ 8.20 m

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
एक व्यक्ति नदी के किनारे खड़े होकर देखता है कि नदी के दूसरे किनारे पर एक पेड़ के शीर्ष का उन्नयन कोण 60° है। जब वह किनारे से 21 m पीछे की ओर चलता है, तो वह उन्नयन कोण 30° पाता है। पेड़ की ऊँचाई तथा नदी की चौड़ाई ज्ञात कीजिए।
हल

प्रश्न 2.
एक मनुष्य पानी के जहाज की छत जो पानी की सतह से 10 m ऊपर है, पर खड़ा है। वहाँ से पहाड़ी की चोटी का उन्नयन कोण 60° तथा पहाड़ की तली का अवनमन कोण 30° है। जहाज से पहाड़ी की दूरी और पहाड़ी की ऊँचाई ज्ञात कीजिए।
हल

माना AB एक जहाज तथा CD एक पहाड़ी है। पहाड़ी की चोटी का उन्नयन कोण ∠CAE = 60°
तथा पहाड़ी की तली का अवनमन कोण ∠EAD = 30° है।
जबकि AE, A से CD पर लम्ब है।
माना पहाड़ी की ऊँचाई h m और जहाज से पहाड़ी की दूरी x m है।
CE = (h – 10) m

प्रश्न 3.
एक मकान के आधार से 30 m दूरस्थ एक मीनार के शिखर का उन्नयन कोण 60° तथा मकान की छत से उसी मीनार के शिखर का उन्नयन कोण 45° है। मकान तथा मीनार की ऊँचाई ज्ञात कीजिए।
हल

माना AB मकान तथा PQ मीनार है।
तब प्रश्नानुसार, BQ = 30 m,
∠PBQ = 60° तथा ∠PAM = 45°
माना मीनार की ऊँचाई H तथा मकान की ऊँचाई h है।

⇒ H – h = 30
⇒ h = H – 30 = 30√3 – 30 = 30(√3 – 1) m
अत: मकान की ऊँचाई 30(√3 – 1) m तथा मीनार की ऊँचाई 303 m है।

प्रश्न 4.
किसी मीनार के आधार से a और b दूरी पर एक ही रेखा में स्थित दो बिन्दुओं क्रमशः A और B से देखने पर मीनार के ऊपरी सिरे के उन्नयन कोण पूरक पाये जाते हैं। सिद्ध कीजिए कि मीनार की ऊँचाई √ab है।
हल

माना मीनार OC की ऊँचाई = h m तथा मीनार का आधार OA है।
माना आधार पर (एक ही रेखा पर) दो बिन्दु A तथा B इस प्रकार हैं कि
OA = a तथा OB = b
क्योंकि A तथा B पर बनने वाले कोण पूरक हैं।
अत: यदि ∠CAO = θ
तब ∠CBO = 90° – θ
समकोण ∆COA में,

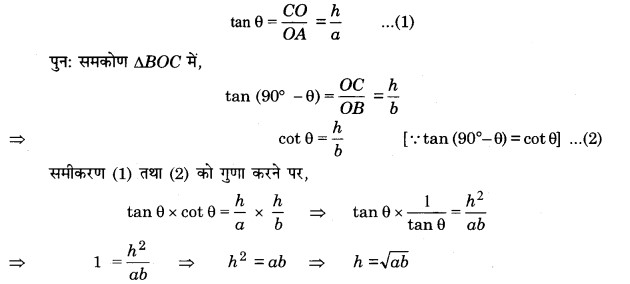
प्रश्न 5.
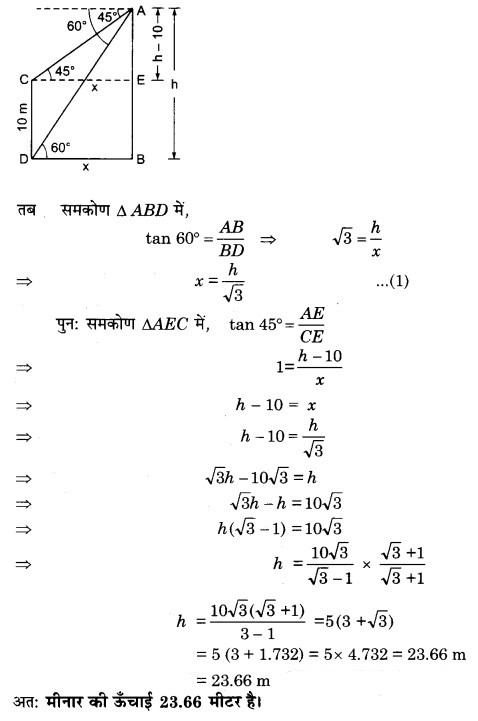
सड़क के एक ओर स्थित मकान के, सड़क के दूसरी ओर स्थित मीनार के शिखर से मकान की छत और आधार के अवनमन कोण क्रमश: 45° और 60° हैं। यदि मकान की ऊँचाई 10 m है, तो मीनार की ऊँचाई ज्ञात कीजिए।
हल
माना AB मीनार तथा CD मकान है।
माना BD = x तथा मीनार की ऊँचाई = h m

प्रश्न 6.
एक अपूर्ण मन्दिर के आधार से 30 m दूर स्थित किसी बिन्दु से उसके शिखर का उन्नयन कोण 30° है। मन्दिर कितना ऊँचा और बनाया जाये कि उसी बिन्दु पर उन्नयन कोण 45° हो जाये (दिया है, √3 = 1.732)।
हल
माना बिन्दु D से देखने पर अपूर्ण मन्दिर AB के शिखर B का उन्नयन कोण 30° है।
∠BDA = 30°
माना मन्दिर की ऊँचाई BC बढ़ाने पर उसके शिखर C का उन्नयन कोण 45° हो जाता है।

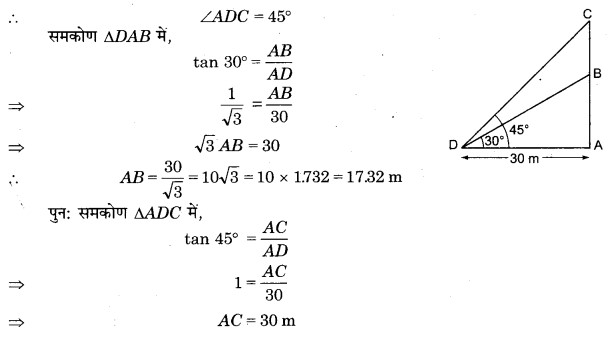
∴ BC = AC – AB = 30 – 17.32 = 12.68 m
अत: मन्दिर को 1268 m ऊँचाई तक और बनवाना पड़ेगा।

प्रश्न 7.
एक नाव से जो पुल की ओर आ रही है, उस पुल का उन्नयन कोण 30° देखा गया। नाव के उसी चाल से 6 min पश्चात् उन्नयन कोण 60° हो गया। ज्ञात कीजिए नाव को उस पुल तक उसी चाल से पहुँचने में कितना समय और लगेगा?
हल
माना P पुल है और नाव की प्रथम स्थिति A है जहाँ से पुल P का उन्नयन कोण 30° है।
6 m बाद नाव की द्वितीय स्थिति B है जहाँ से पुल का उन्नयन कोण 60° है।

प्रश्न 8.
एक वायुयान दो मकानों के ऊपर से उड़ रहा है जिनके बीच की न्यूनतम दूरी 300 m है। यदि किसी समय वायुयान से एक ही दिशा में दोनों मकानों के अवनमन कोण क्रमशः 45° और 60° हैं, तो ज्ञात कीजिए कि वायुयान कितनी ऊँचाई पर उड़ रहा है?
हल

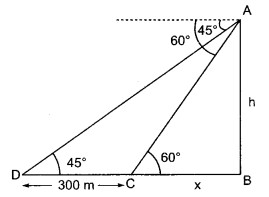
माना वायुयान A की ऊँचाई AB है।
तथा C व D क्रमश: दो मकान हैं जबकि CD = 300 m
माना वायुयान की ऊँचाई h है तथा BC = x
तब समकोण ∆ABC में,

प्रश्न 9.
एक हवाई जहाज जो कि 1000 m की ऊँचाई पर उड़ रहा है, पर स्थित मनुष्य उत्तर की ओर एक शत्रु की पनडुब्बी को 30° के अवनमन कोण पर तथा दक्षिण की ओर एक युद्धपोत को 45° के अवनमन कोण पर देखता है। पनडुब्बी और युद्धपोत के बीच की दूरी ज्ञात कीजिए।
हल

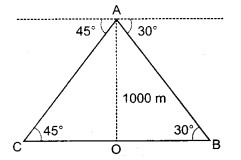
माना हवाई जहाज की स्थिति A, पनडुब्बी की स्थिति Bव युद्धपोत की स्थिति C है तब प्रश्नानुसार,
∠ABC = 30°, ∠ACB = 45°
तथा AO = 1000 m (जबकि AO ⊥ BC)

BO = 1000√3
∴ पनडुब्बी व युद्धपोत के बीच की दूरी, BC = (BO + OC)
= (1000√3 + 1000)
= 1000(√3 + 1) m

प्रश्न 10.
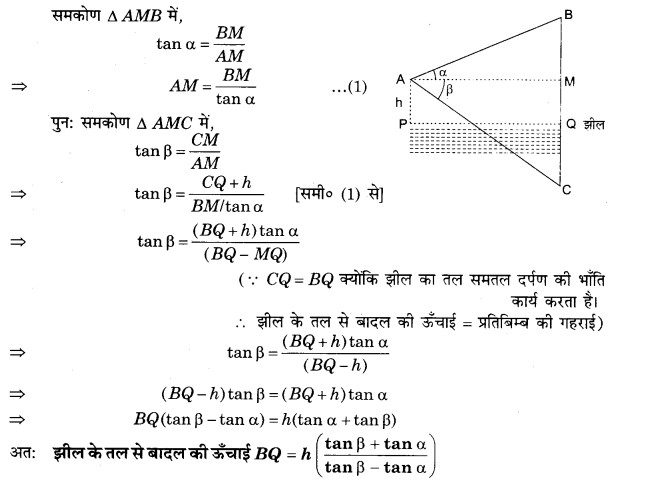
एक झील के तल से h मीटर ऊँचाई पर स्थित एक बिन्दु पर एक बादल का उन्नयन कोण α है तथा झील में उसके प्रतिबिम्ब का अवनमन कोण β है। सिद्ध कीजिए कि झील के तल से बादल की ऊँचाई  है।
हल
माना PQ झील का तल व झील से h ऊँचाई पर बिन्दु A है।
बिन्दु A से बादल B का उन्नयन कोण ∠BAM = α
तथा बादल के प्रतिबिम्ब C का अवनमन कोण ∠MAC = β

tense in english