bihar board class 10th maths | Introduction to Trigonometry
bihar board class 10th maths | Introduction to Trigonometry
Bihar Board Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry
प्रश्नावली 8.1
प्रश्न 1. ΔABC में, जिसका कोण B समकोण है, AB = 24 सेमी और BC = 7 सेमी है। निम्नलिखित का मान ज्ञात कीजिए-
(i) sin A, cos A
(ii) sin C, cos C

हल:
समकोण ΔABC में ∠B = 90°
तब पाइथागोरस प्रमेय से,
AC2 = AB2 + BC2
AC2 = (24)2 + (7)2 = 576 + 49 = 625
AC = √625 = 25 सेमी

प्रश्न 2. आकृति में, tan P – cot R का मान ज्ञात कीजिए।
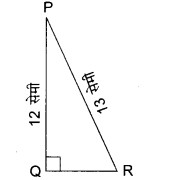
हल:
समकोण ΔPQR में,
पाइथागोरस प्रमेय से,
PQ2 + QR2 = PR2
⇒ (12)2 + QR2 = (13)2
⇒ QR2 = (13)2 – (12)2 = 169 – 144 = 25
⇒ QR = 5 सेमी

प्र० 3. यदि sin A = , तो cos A और tan A का मान परिकलित कीजिए।
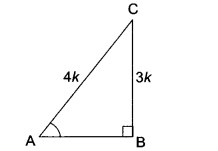
हल:

प्रश्न 4. यदि 15 cot A = 8 हो, तो sin A और sec A का मान ज्ञात कीजिए।

हल:

प्रश्न 5. sec θ = , हो तो अन्य सभी त्रिकोणमितीय अनुपात परिकलित कीजिए।
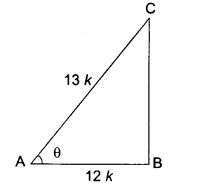
हल:

प्रश्न 6. यदि ∠A तथा ∠B न्यूनकोण हों और cos A = cos B हो, तो दिखाइए कि: ∠A = ∠B
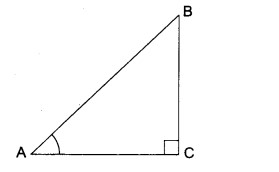
हल:
माना त्रिभुज ABC में ∠C समकोण है।
दिया है, ∠A तथा ∠B न्यूनकोण हैं।

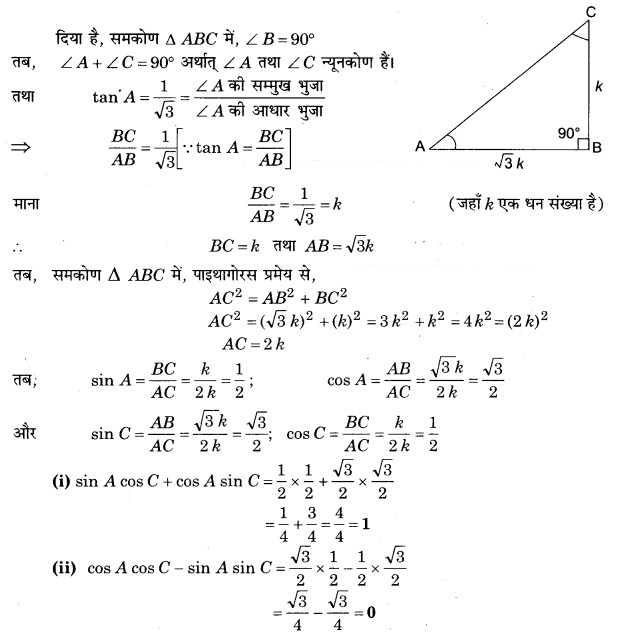
प्र० 9. त्रिभुज ABC में, जिसका कोण B समकोण है, यदि tan A = , तो निम्नलिखित के मान ज्ञात कीजिए:
(i) sin A cos C + cos A sin C
(ii) c0s A cos C sin A sin C
हल:
प्रश्न 10. ΔPQR में, जिसका कोण Q समकोण है, PR + QR = 25 सेमी और PQ = 5 सेमी है। sin P, cos P और tan P के मान ज्ञात कीजिए।
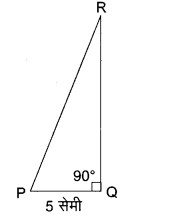
हल:
दिया है, समकोण ΔPQR में, ∠Q = 90°
पाइथागोरस प्रमेय से,
PQ2 + QR2 = PR2
⇒ (5)2 + QR2 = PR2
⇒ 25 = PR2 – QR2
⇒ 25 = (PR + QR) (PR – QR) [∵ a2 – b2 = (a + b)(a – b)]
⇒ 25 = 25 (PR – QR) (∵ PR + QR = 25, दिया है)
⇒ PR – QR = 1 ……..(1)
और PR + QR = 25 ……(2)
समीकरण (1) व (2) को हल करने पर,
PR = 13 सेमी तथा QR = 12 सेमी
समकोण ΔPQR में,
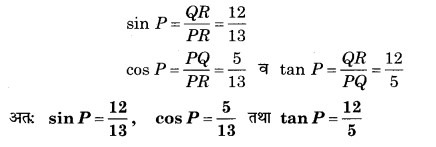
प्र० 11. बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) tan A को मान सदैव 1 से कम होता है।
(ii) कोण A के किसी मान के लिए sec A =
(iii) cos A, कोण A के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
(iv) cot A, cot और A का गुणनफल होता है।
(v) किसी भी कोण 8 के लिए sin θ =
हलः
(i) असत्यः [चूकि, समकोण त्रिभुज में कर्ण के अतिरिक्त अन्य दो भुजाओं का अनुपात 1 के समान या असमान हो सकता है।]
(ii) सत्यः [ cos A का मान सदैव 1 से कम होता है।
अर्थात् sec A का मान 1 से सदैव बड़ा होता है।]
(iii) असत्यः [cosine A को संक्षिप्त रूप ‘cos A’ होता है।]
(iv) असत्यः [अकेले ‘cot’ का कोई अर्थ नहीं है। cot A एक ही त्रिकोणमितीय अनुपात होता है।]
(v) असत्यः [का मान 1 से अधिक है, जबकि sin 8 का मान 1 से अधिक नहीं हो सकता]
प्रश्नावली 8.2
प्रश्न 1. निम्नलिखित के मान निकालिए
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan2 45° + cos2 30° – sin2 60°

हल:
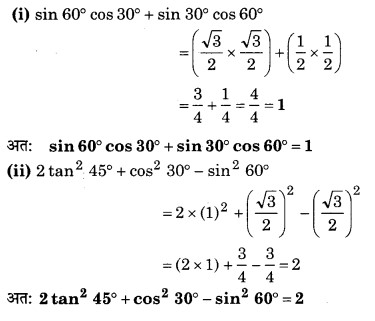



प्रश्न 2. सही विकल्प चुनिए और अपने विकल्प का औचित्य दीजिए :
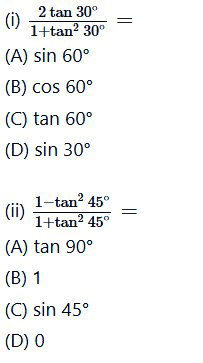
(iii) sin 2A = 2sin A तब सत्य होता है, जबकि A बराबर है :
(A) 0°
(B) 30°
(C) 45°
(D) 60°

हल:

प्रश्न 3. यदि tan (A + B) = √3 और tan (A B) = ; 0° < A + B ≤ 90°; A > B तो A और B का मान ज्ञात कीजिए।
हलः तालिका से, हमें प्राप्त होता है:
tan 60° = √3 …(1)
चूंकि tan (A + B) = √3 [ज्ञात है] …(2)
(1) और (2) से, हमें प्राप्त होता है।
A + B = 60° ………(3)
इसी प्रकार,
A B = 30° ………. (4)
(3) और (4) को जोड़ने पर, 2A = 90° ⇒ A = 45°
(3) में से (4) को घटाने पर, 2B = 30° ⇒ B = 15°
प्रश्न 4. बताइए कि निम्नलिखित में कौनकौन सत्य हैं या असत्य हैं। कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) sin (A + B) = sin A + sin B.
(ii) θ में वृद्धि होने के साथ sin θ के मान में भी वृद्धि होती है।
(iii) θ में वृद्धि होने के साथ cos θ के मान में भी वृद्धि होती है।
(iv) θ के सभी मानों पर sin θ = cos θ
(v) A = 0° पर cot A परिभाषित नहीं है।
हलः (i) माना
A = 30° और B = 60°
L.H.S. = sin (30° + 60°) = sin 90° = 1
R.H.S. = sin 30° + sin 60° =
L.H.S. ≠ R.H.S.
कथन “sin (A+ B) = sin A + sin B” असत्य है।
(ii) चूँकि “जब θ का मान 0° से 90° तक बढ़ता है तो sin θ का मान 0 से 1 तक बढ़ता है।”
दिया गया कथन सही है।
(iii) चूँकि “जब θ का माप 0° से 90° तक बढ़ता है, तो cos θ का मान 1 से 0 तक घटता है।”
दिया गया कथन असत्य है।
(iv) माना θ = 30° है।
तालिका से हमें प्राप्त होता है: sin 30° = और cos 30° =
sin 30° ≠ cos 30°
अतः दिया गया कथन असत्य है।
(v) तालिका से हमें प्राप्त है: cot 0° = अपरिभाषित
अतः दिया गया कथन सत्य है।
प्रश्नावली 8.3
प्रश्न 1. निम्नलिखित का मान निकालिएः
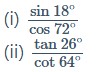
(iii) cos 48° – sin 42°
(iv) cosec 31° – sec 59°
हल:
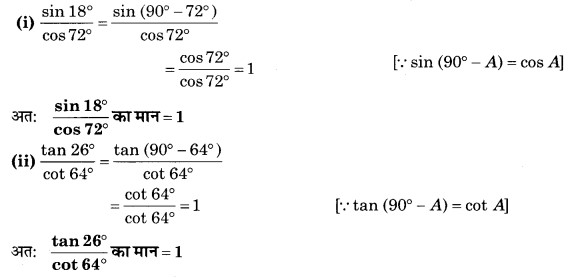
(iii) cos 48° – sin 42°
= cos (90° – 42°) – sin 42°
= sin 42° – sin 42°
= 0 [∵ cos (90° – A) = sin A]
अतः cos 48° – sin 42° = 0
(iv) cosec 31° – sec 59°
= cosec (90° – 59°) – sec 59°
= sec 59° – sec 59°
= 0 [∵ cosec (90° – A) = sec A]
अतः cosec 31° – sec 59° = 0
प्रश्न 2. दिखाइए कि
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
हल:
(i) L.H.S. = tan 48° tan 23° tan 42° tan 67°
= tan 48° tan 23° tan (90° – 48°) tan (90° – 23°)
= tan A tan B tan (90° – A) tan (90° – B) [माना A = 48°, B = 23°]
= tan A tan B cot A cot B
![]()
= 1
= R.H.S.
L.H.S. = R.H.S.
(ii) L.H.S. = cos 38° cos 52° – sin 38° sin 52°
= cos 38° cos (90° – 38°) – sin 38° sin (90° – 38°)
= cos A cos (90° – A) sin A sin (90° – A) [यदि 38° = A हो]
= cos A sin A – sin A cos A [∵ cos (90° – A) = sin A और sin (90° – A) = cos A]
= sin A cos A – sin A cos A
= 0
= R.H.S.
L.H.S.= R.H.S.
प्रश्न 3. यदि tan 2A = cot (A – 18°), जहाँ 2A एक न्यूनकोण है, तो A का मान ज्ञात कीजिए|
हल: tan 2A = cot (A – 18°),
⇒ cot (90° – 2A) = cot(A – 18°)
दोनों पक्षों में तुलना करने पर
⇒ 90° – 2A = A – 18°
⇒ 90° + 18° = A + 2A
⇒ 3A = 108°
⇒ A = 36°
प्रश्न 4. यदि tan A = cot B, तो सिद्ध कीजिए कि A + B = 90°
हल: tan A = cot B दिया है |
⇒ tan A = tan (90° – B)
तुलना करने पर
⇒ A = 90° – B
⇒ A + B = 90°
Proved.
प्रश्न 5. यदि sec 4A = cosec(A – 20°), जहाँ 4A एक न्यूनकोण है, तो A का मान ज्ञात कीजिए।
हल: दिया है, sec 4A = cosec(A – 20°)
⇒ cosec (90° – 4A) = cosec (A – 20°) [∵ sec θ = cosec (90° – θ)]
⇒ 90° – 4A = A – 20°
⇒ A + 4A = 90° + 20°
⇒ 5A = 110°
⇒ A = 22°
अत: A का मान = 22°
प्रश्न 6. यदि A, B और C त्रिभुज ABC के अन्तःकोण हों, तो दिखाइए कि ![]()
हल: हम जानते हैं कि त्रिभुज के अन्तःकोणों का योग = 180°
A + B + C = 180°
⇒ (B + C) = 180° – A

प्रश्न 7. sin 67° + cos 75° को 0° और 45° के बीच के कोणों के त्रिकोणमितीय अनुपातों के पदों में व्यक्त कीजिए।
हल: दिया है, sin 67° + cos 75°
= sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15°
अत: sin 67° + cos 75° = cos 23° + sin 15°
प्रश्नावली 8.4
प्रश्न 1. त्रिकोणमितीय अनुपातों sin A, sec A और tan A को cot A के पदों में व्यक्त कीजिए
हल: हम जानते हैं कि cot A और cosec A में सम्बन्ध ‘cosec2 A = 1 + cot2 A’ है और cosec A और sin A में सम्बन्ध प्रतिलोम का है।
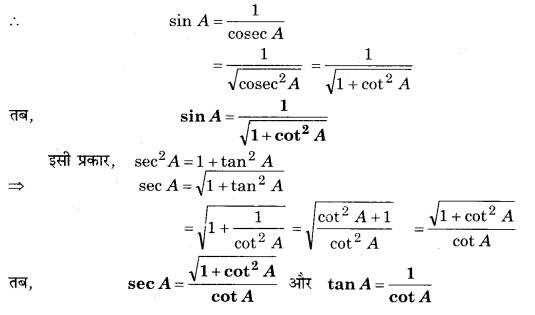
प्रश्न 2. ∠A के अन्य सभी त्रिकोणमितीय अनुपातों को sec A के पदों में लिखिए।
हल:

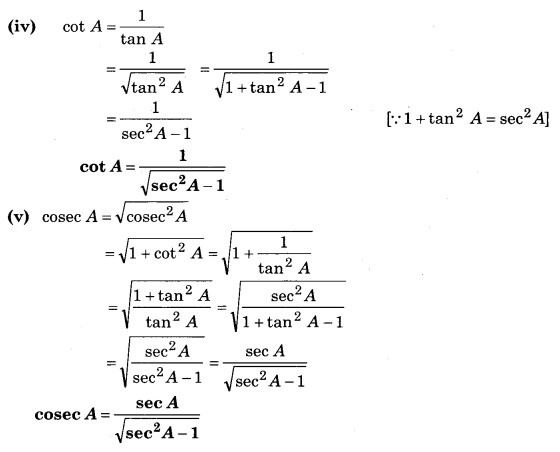
प्रश्न 3.

(ii) sin 25° cos 65° + cos 25° sin 65°
हल:
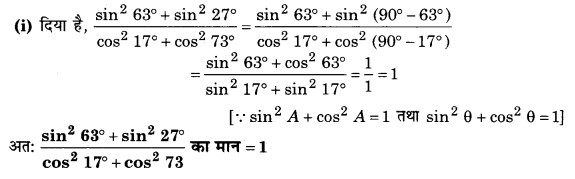
(ii) दिया है, sin 25° cos 65° + cos 25° sin 65°
= sin 25° cos (90° – 25°) + cos 25° sin (90° – 25°)
= sin 25° sin 25° + cos 25° cos 25°
[∵ cos (90° – 25°) = sin 25° तथा sin(90° – 25°) = cos 25°]
= sin2 25° + cos2 25°
= 1 [∵ sin2 A+ cos2 A = 1]
अतः sin 25° cos 65° + cos 25° sin 65° = 1
प्रश्न 4. सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए-
(i) 9 sec2 A – 9 tan2 A बराबर है-
(A) 1
(B) 9
(C) 8
(C) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) बराबर है-
(A) 0
(B) 1
(C) 2
(D) -1
(iii) (sec A + tan A)(1 – sin A) बराबर है-
(A) sec A
(B) sin A
(C) cosec A
(D) cos A

हल:
(i) यहाँ 9 sec2 A – 9 tan2 A
= 9 (sec2 A – tan2 A)
= 9 (1 + tan2 A – tan2 A) [∵ sec2 A = 1 + tan2 A]
= 9 × (1)
= 9
अत: विकल्प (B) सही है।
(ii) यहाँ (1 + tan θ + sec θ) (1 + cot θ – cosec θ)


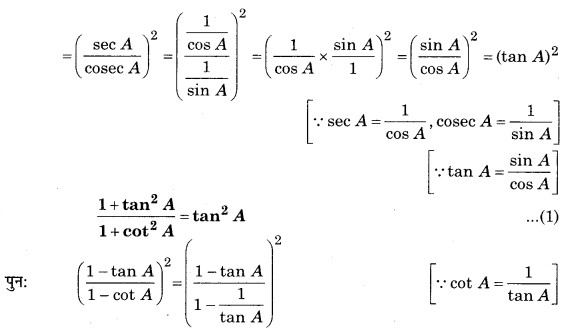
प्रश्न 5. निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यूनकोण हैं-
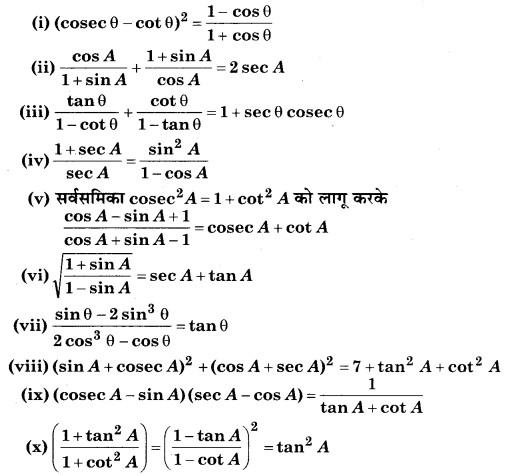
हल:





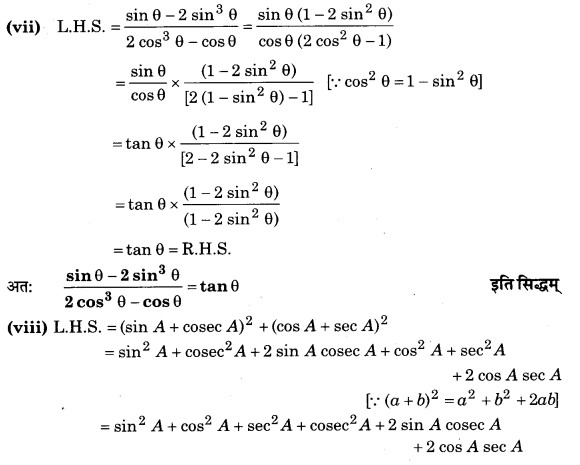
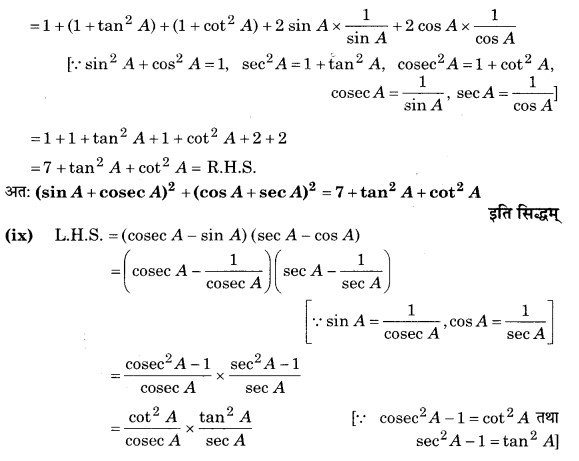

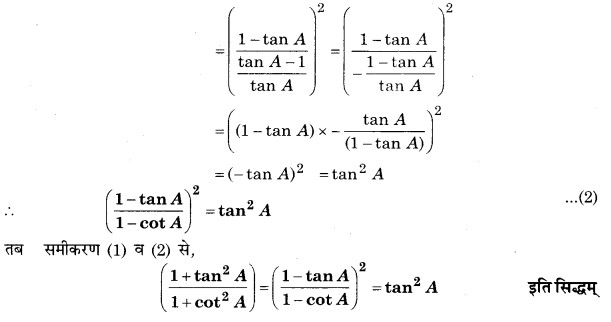
त्रिकोणमिति का परिचय Additional Questions
बहुविकल्पीय प्रश्न
प्रश्न 1.
व्यंजक [cosec(75° + θ) – sec(15° – θ) – tan(55° + θ) + cot(35° – θ)] का मान है
(i) -1
(ii) 0
(iii) 1
(iv) 3/2
हल
(ii) 0
प्रश्न 2.
यदि cos(α + β) = 0 हो, तो sin(α – β) को निम्नलिखित के रूप में बदला जा सकता है-
(i) cos β
(ii) cos 2β
(iii) sin θ
(iv) sin 2α
हल
(ii) cos 2β
प्रश्न 3.
(tan 1° tan 2° tan 3°…tan 89°) का मान है
(i) 0
(ii) 1
(iii) 2
(iv) 1/2
हल
(ii) 1
प्रश्न 4.
यदि cos 9α = sin α है और 9α < 90° है, तो tan 5α का मान है
(i) 1/√3
(ii) √3
(iii) 1
(iv) 0
हल
(iii) 1
प्रश्न 5.
यदि ∆ABC एक समकोण त्रिभुज है जिसमें कोण C समकोण है, तो cos(A + B) का मान है
(i) 0
(ii) 1
(iii) 1/2
(iv) √3/2
हल
(i) 0
प्रश्न 6.
यदि sin A + sin2 A = 1 है, तो व्यंजक (cos2 A + cos4 A) का मान है
(i) 1
(ii) 1/2
(iii) 2
(iv) 3
हल
(i) 1
प्रश्न 7.
sin(45° + θ) – cos(45° – θ) बराबर है
(i) 2 cos θ
(ii) 0
(iii) 2 sin θ
(iv) 1
हल
(ii) 0
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
cot A का मान ज्ञात कीजिए, यदि 3 cos A – 4 sin A = 2 cos A + 3 sin A
हल
दिया है, 3 cos A – 4 sin A = 2 cos A + 3 sin A
⇒ 3 cos A – 2 cos A = 3 sin A + 4 sin A
⇒ cos A = 7 sin A
![]()
⇒ cot A = 7
प्रश्न 2.
त्रिभुज ABC में यदि AB = BC, ∠B = 90° है तो निम्न के मान ज्ञात कीजिए
(i) sin A
(ii) cos A
हल
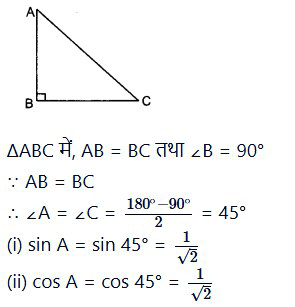
प्रश्न 3.
cot 80° cot 10° – tan 80° tan 10° का मान ज्ञात कीजिए।
हल
यहाँ, cot 80° cot 10° – tan 80° tan 10°
= cot(90° – 10°) . cot (90° – 80°) – tan 80° tan 10°
= tan 80° tan 10° – tan 80° tan 10°
= 0
प्रश्न 4.
सिद्ध कीजिए की

हल

प्रश्न 5.
cos 80° cos 70° – cos 10° cos 20° का मान ज्ञात कीजिए।
हल
cos 80° cos 70° – cos 10° cos 20°
= cos 80° cos 70o – cos(90° – 80°) cos(90° – 70°)
= cos 80° cos 70° – sin 80° sin 70° [∵ cos (90° – θ) = cos θ]
= cos(80° + 70° )
= cos 150°
= cos(180° – 30°)
= -cos 30° [∵ cos (180° – θ) = -cos θ]
= −√3/2
प्रश्न 6.
सिद्ध कीजिए की (1 – sin θ) (1 + sin θ) (1 + tan2 θ) = 1
हल
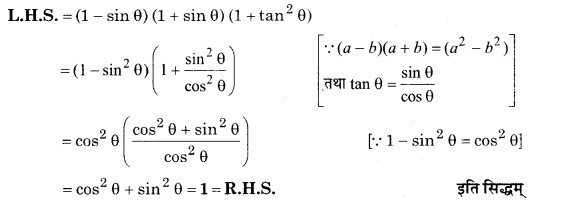
प्रश्न 7.
सिद्ध कीजिए tan2 θ + cot2 θ = sec2 θ cosec2 θ – 2
हल
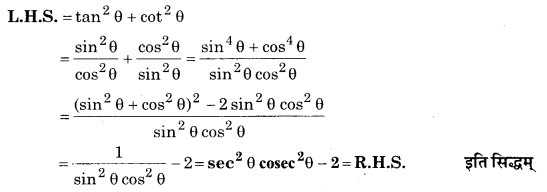
प्रश्न 8.
सिद्ध कीजिए (cosec A – sin A) (sec A – cos A) (tan A + cot A) = 1
हल
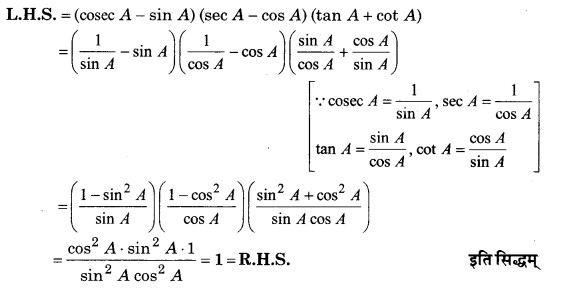
प्रश्न 9.
सिद्ध कीजिए

हल
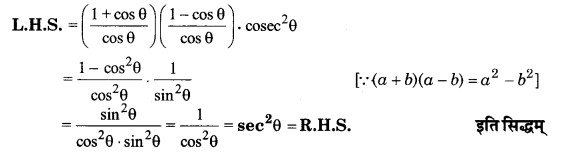
लघु उत्तरीय प्रश्न
प्रश्न 1.
सिद्ध कीजिए कि
![]()
हल
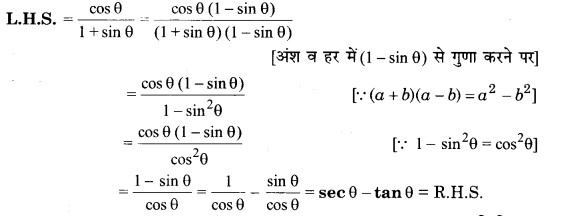
प्रश्न 2.
सिद्ध कीजिए

हल

प्रश्न 3.
सिद्ध कीजिए की
![]()
हल
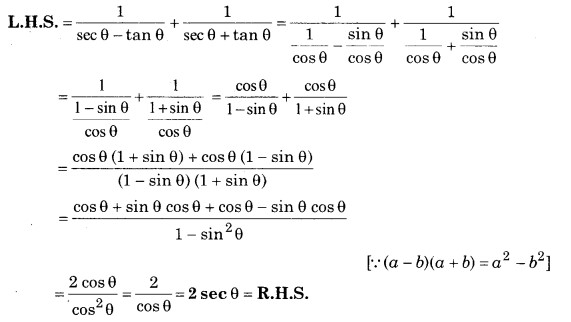
प्रश्न 4.
सिद्ध कीजिए की
![]()
हल
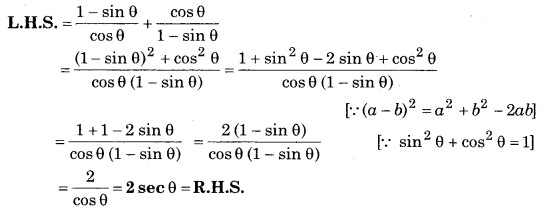
प्रश्न 5.
सिद्ध कीजिए की

हल

प्रश्न 6.
सिद्ध कीजिए

हल
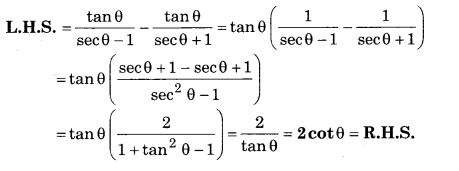
प्रश्न 7.
यदि x = r cos θ cos α, y = r sin θ cos α तथा z = r sin α, तो सिद्ध कीजिए की x2 + y2 + z2
हल
L.H.S. = x2 + y2 + z2
= (r cos θ cos α)2 +(r sin θ cos α)2 + (r sin α)2
= r2 cos2 θ cos2 α + r2 sin2 θ cos2 α + r2 sin2 α
= r2 cos2 α (cos2 θ + sin2 θ) + r2 sin2 α
= r2 cos2 α . 1 + r2 sin2 α [∵ sin2 θ + cos2 θ = 1]
= r2 (cos2 α + sin2 α)
= r2 . 1
= r2
= R.H.S.
प्रश्न 8.
यदि tan θ + sin θ = p तथा tan θ – sin θ = q तो सिद्ध कीजिए p2 – q2 = 4√pq
हल
L.H.S. = p2 – q2
= (p + q) (p – q)
= (tan θ + sin θ + tan θ – sin θ) (tan θ + sin θ – tan θ + sin θ)
= 2 tan θ . 2 sin θ
= 4 tan θ sin θ
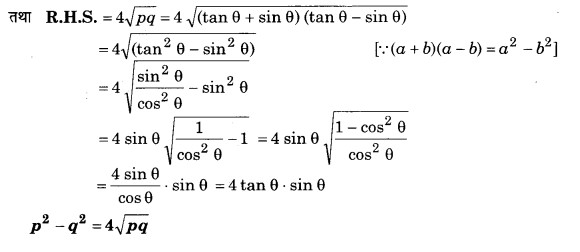
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
दी गई आकृति में ABC एक समकोण त्रिभुज है। D, BC का मध्य-बिन्दु है :

हल

प्रश्न 2.
मान ज्ञात कीजिए :

हल
