bihar board class 10th maths | Arithmetic Progressions

Bihar Board Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions

प्रश्नावली 5.1

प्रश्न 1. निम्नलिखित स्थितयों में से किन स्थितयों में संबद्ध संख्याओं की सूची A.P है और क्यों?
(i) प्रत्येक किलों मीटर के बाद टैक्सी का किराया, जबकि प्रथम किलो मीटर के लिए किराया 15 रु है और प्रत्येक अतिरिक्त किलो मीटर के लिए किराया 8 रु है|
(ii) किसी बेलन (cylinder) में उपस्थित हवा की मात्रा, जबकि वायु निकालने वाला पम्प प्रत्येक बार बेलन की हवा का भाग बाहर निकाल देता है|
(iii) प्रत्येक मीटर की खुदाई के बाद, एक कुआं खोदने में आई लागत, जबकि प्रथम मीटर खुदाई की लागत 150 रु है और बाद में प्रत्येक खुदाई की लागत 50 रुo बढ़ती जाती है|
(iv) खाते में प्रत्येक वर्ष का मिश्रधन, जबकि 10000 रुo की राशि 8 % वार्षिक की दर से चक्रवृद्धि ब्याज पर जमा की जाती है|
हल:
(i) टैक्सी के प्रथम किमी का किराया = ₹ 15
अगले प्रत्येक किमी का किराया = ₹ 8
2 किमी का किराया = ₹ (15 + 8) = ₹ 23
3 किमी का किराया = ₹ (23 + 8) = ₹ 31
4 किमी का किराया = ₹ (31 + 8) = ₹ 39
a₁ = ₹ 15, a₂ = ₹ 23, a₃ = ₹ 31, a₄ = ₹ 39
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = ₹ (23 – 15) = ₹ 8
a₃ – a₂ = ₹ (31 – 23) = ₹ 8
a₄ – a₃ = ₹ (39 – 31) = ₹ 8
दो क्रमागत पदों का अन्तर नियत है,
अत: किमी में टैक्सी का किराया A.P. में है।

(ii) माना बेलन में हवा का प्रारम्भिक आयतन = V

दो क्रमागत पदों का अन्तर नियत नहीं है,
अत: हवा के आयतन A.P. में नहीं हैं।

(iv) खाते में जमा किए गए धन के लिए भिन्न वर्षों के मिश्रधन :
मूलधन, P = ₹ 10000, ब्याज की दर, R = 8%

निरीक्षण से ही स्पष्ट है कि A₂ – A₁ ≠ A₃ – A₂
अत: मिश्रधन A.P. में नहीं हैं।

प्रश्न 2. दी हुई A.P के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अंतर d निम्नलिखित हैं :
(i) a = 10, d = 10
(ii) a = -2, d = 0
(iii) a = 4, d = -3
(iv) a = -1, d = 
(v) a = -1.25, d = -0.25
हल:
(i) प्रथम पद (a) = 10 तथा सार्वान्तर (d) = 10
दूसरा पद = a + d = 10 + 10 = 20
तीसरा पद = a + 2d = 10 + (2 × 10) = 30
चौथा पद = a + 3d = 10 + (3 × 10) = 40
अत: दी गई A.P. के प्रथम चार पद : 10, 20, 30, 40

(ii) प्रथम पद (a) = -2 तथा सार्वान्तर (d) = 0
दूसरा पद = a + d = -2 + 0 = -2
तीसरा पद = a + 2d = -2 + (2 × 0) = -2
चौथा पद = a + 3d = -2 + (3 × 0) = -2
अतः दी गई A.P. के प्रथम चार पद : -2, -2, -2, -2

(iii) प्रथम पद (a) = 4 तथा सार्वान्तर (d) = -3
दूसरा पद = a + d = 4 + (-3) = 1
तीसरा पद = a + 2d = 4 + 2 × (-3) = 4 + (-6) = -2
चौथा पद = a + 3d = 4 + 3 × (-3) = 4 + (-9) = -5
अत: दी गई A.P. के प्रथम चार पद : 4, 1, -2, -5

(v) प्रथम पद (a) = -1.25 तथा सार्वान्तर (d) = -0.25
दूसरा पद = a + d = -1.25 + (-0.25) = -1.50
तीसरा पद = a + 2d = -1.25 + 2 × (-0.25) = -1.25 – 0.50 = -1.75
चौथा पद = a + 3d = -1.25 + 3 × (-0.25) = -1.25 – 0.75 = -2.00
अतः दी गई A.P. के प्रथम चार पद : -1.25, -1.50, -1.75, -2.00

प्रश्न 3. निम्नलिखित में से कौन-कौन A.P हैं? यदि कोई A.P है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन पद लिखिए |
(i) 3, 1, -1, -3, ……
(ii) -5, -1, 3, 7, ……
(iii) , , , 
(iv) 0.6, 1.7, 2.8, 3.9
हल:
(i) दी गई A.P. = 3, 1, -1, -3,…….
a₁ = 3, a₂ = 1, a₃ = -1, a₄ = -3
प्रथम पद (a) = a₁ = 3
सार्वान्तर (d) = a₂ – a₁ = 1 – 3 = -2
अत: प्रथम पद = 3 तथा सार्वान्तर = -2

(ii) दी गई A.P. = -5, -1, 3, 7,…….
a₁ = -5, a₂ = -1, a₃ = 3, a₄ = 7
प्रथम पद (a) = a₁ = -5
सार्वान्तर (d) = a₂ – a₁ = -1 – (-5) = -1 + 5 = 4
अत: प्रथम पद = -5 तथा सार्वान्तर = 4

(iv) दी गई A.P. = 0.6, 1.7, 2.8, 3.9,……
a₁ = 0.6, a₂ = 1.7, a₃ = 2.8, a₄ = 3.9
प्रथम पद (a) = a₁ = 0.6
सार्वान्तर (d) = a₂ – a₁ = 1.7 – 0.6 = 1.1
अतः प्रथम पद = 0.6 तथा सार्वान्तर = 1.1

प्रश्न 4. निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्वान्तर ज्ञात कीजिए और इनके तीन और पद लिखिए।
(i) 2, 4, 8, 16, …….

(iii) -1.2, -3.2, -5.2, -7.2,…..
(iv) -10, -6, -2, 2,…….
(v) 3, 3 + √2, 3 + 2√2, 3 + 3√2,….
(vi) 0.2, 0.22, 0.222, 0.2222,….
(vii) 0, -4, -8, -12,……

(ix) 1, 3, 9, 27,……
(x) a, 2a, 3a, 4a,……
(xi) a, a², a³, a⁴,……
(xii) √2, √8, √18, √32,……
(xiii) √3, √6, √9, √12,…..
(xiv) 1², 3², 5², 7²,…..
(xv) 1², 5², 7², 73,……
हल:
यहाँ प्रत्येक अनुक्रम के प्रथम 4 पद ज्ञात हैं। यदि कोई अनुक्रम A.P. में है, तो उसके अगले तीन पद और ज्ञात करने हैं अर्थात् 5 वाँ, छठा और 7 वाँ पद और ज्ञात करना है।
(i) दिया हुआ अनुक्रम : 2, 4, 8, 16, ……..
a₁ = 2, a₂ = 4, a₃ = 8, a₄ = 16
दो क्रमागत पदों के अन्तर,
a₂ – a₁ = 4 – 2 = 2
a₃ – a₂ = 8 – 4 = 4
दो क्रमागत पदों का अन्तर नियत नहीं है।
अतः दिया गया अनुक्रम A.P. में नहीं है।

(ii) दिया हुआ अनुक्रम,

(iii) दिया हुआ अनुक्रम : -1.2, -3.2, -5.2, -7.2, ……
a₁ = -1.2, a₂ = -3.2, a₃ = -5.2, a₄ = -7.2
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = -3.2 – (-1.2) = -3.2 + 1.2 = -2.0
a₃ – a₂ = -5.2 – (-3.2) = -5.2 + 3.2 = -2.0
a₄ – a₃ = -7.2 – (-5.2) = -7.2 + 5.2 = -2.0
दो क्रमागत पदों का अन्तर नियत (-2.0) है।
सार्वान्तर d = -2.0 और दिया गया अनुक्रम एक A.P. है।
तब, पाँचवाँ पद (a₅) = चौथा पद (a₄) + सार्वान्तर (d) = -7.2 + (-2) = -9.2
छठा पद (a₆) = पाँचवाँ पद (a₅) + सार्वान्तर (d) = -9.2 + (-2) = -11.2
सातवाँ पद (a₇) = छठा पद (a₆) + सार्वान्तर (d) = -11.2 + (-2)= -13.2
अत: दिए गए अ6नुक्रम के अगले तीन पद : -9.2, -11.2, -13.2 होंगे।

(iv) दिया हुआ अनुक्रम : -10, -6, -2, 2,…..
a₁ = -10, a₂ = -6, a₃ = -2, a₄ = 2
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = -6 – (-10) = -6 + 10 = 4
a₃ – a₂ = -2 – (-6) = -2 + 6 = 4
a₄ – a₃ = 2 – (-2) = 2 + 2 = 4
दो क्रमागत पदों का अन्तर नियत (4) है।
सार्वान्तर (d) = 4 और दिया गया अनुक्रम एक A.P. है।
तब, पाँचवाँ पद (a₅) = चौथा पद (a₄) + सार्वान्तर (d) = 2 + 4 = 6
छठा पद (a₆) = पाँचवाँ पद (a₅) + सार्वान्तर (d) = 6 + 4 = 10
सातवाँ पद (a₇) = छठा पद (a₆) + सार्वान्तर (d) = 10 + 4 = 14
अत: दिए गए अनुक्रम के अगले तीन पद : 6, 10, 14 होंगे।

(v) दिया हुआ अनुक्रम : 3, 3 + √2, 3 + 2√2, 3 + 3√2, ……
a₁ = 3, a₂ = 3 + √2, a₃ = 3 + 2√2, a₄ = 3 + 3√2
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = (3 + √2) – 3 = √2
a₃ – a₂ = (3 + 2√2) – (3 + √2) = √2
a₄ – a₃ = (3 + 3√2) – (3 + 2√2) = √2
दो क्रमागत पदों का अन्तर नियत (√2) है।
सार्वान्तर (d) = √2 और दिया गया अनुक्रम एक A.P. में है।
तब, पाँचवाँ पद (a₅ ) = a₄ + d = 3 + 3√2 + √2 = 3 + √2(3 + 1) = 3 + 4√2
छठा पद (a₆) = a₅ + d = 3 + 4√2 + √2 = 3 + √2(4 + 1) = 3 + 5√2
सातवाँ पद (a₇) = a₆ + d = 3 + 5√2 + √2 = 3 + √2(5 + 1) = 3 + 6√2
अतः दिए गए अनुक्रम के अगले तीन पद हैं :
3 + 4√2, 3 + 5√2, 3 + 6√2

(vi) दिया हुआ अनुक्रम : 0.2, 0.22, 0.222, 0.2222, ….
a₁ = 0.2, a₂ = 0.22, a₃ = 0.222, a₄ = 0.2222
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = 0.22 – 0.2 = 0.02
a₃ – a₂ = 0.222 – 0.22 = 0.002
a₄ – a₃ = 0.222 – 0.222 = 0.0002
दो क्रमागत पदों का अन्तर नियत नहीं है।
अत: दिया गया अनुक्रम A.P. में नहीं है।

(vii) दिया हुआ अनुक्रम : 0, -4, -8, -12, ……
a₁ = 0, a₂ = -4, a₃ = -8, a₄ = -12
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = -4 – 0 = -4
a₃ – a₂ = -8 – (-4) = -8 + 4 = -4
a₄ – a₃ = -12 – (-8) = -12 + 8 = -4
दो क्रमागत पदों का अन्तर नियत (-4) है।
सार्वान्तर (d) = -4 और दिया गया अनुक्रम एक A.P. में है।
तब, पाँचवाँ पद (a₅) = चौथा पद (a₄) + सार्वान्तर (d) = -12 + (-4) = -16
छठा पद (a₆) = पाँचवाँ पद (a₅) + सार्वान्तर (d) = -16 + (-4) = -20
सातवाँ पद (a₇) = छठा पद (a₆) + सार्वान्तर (d) = -20 + (-4) = -24
अत: दिए गए अनुक्रम के अगले तीन पद : -16, -20, -24 होंगे।

(viii) दिया हुआ अनक्रम :

(ix) दिया हुआ अनुक्रम : 1, 3, 9, 27,……
a₁ = 1, a₂ = 3, a₃ = 9, a₄ = 27
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = 3 – 1 = 2
a₃ – a₂ = 9 – 3 = 6
a₄ – a₃ = 27 – 9 = 18
दो क्रमागत पदों का अन्तर नियत नहीं है।
अत: दिया गया अनुक्रम एक A.P. में नहीं है।

(x) दिया हुआ अनुक्रम : a, 2a, 3a, 4a, ……
a₁ = a, a₂ = 2a, a₃ = 3a, a₄ = 4a
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = 2a – a = a
a₃ – a₂ = 3a – 2a = a
a₄ – a₃ = 4a – 3a = a
दो क्रमागत पदों का अन्तर नियत (a) है।
अतः सार्वान्तर (d) = a और दिया गया अनुक्रम एक A.P. में है।
तब, पाँचवाँ पद (a₅) = चौथा पद (a₄) + सार्वान्तर (d) = 4a + a = 5a
छठा पद (a₆) = पाँचवाँ पद (a₅) + सार्वान्तर (d) = 5a + a = 6a
सातवाँ पद (a₇) = छठा पद (a₆) + सान्तिर (d) = 6a + a = 7a
अतः दिए गए अनुक्रम के अगले तीन पद : 5a, 6a, 7a होंगे।

(xi) दिया हुआ अनुक्रम : a, a², a³, a⁴,……
a₁ = a, a₂ = a², a₃ = a³, a₄ = a⁴
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = a² – a = a(a – 1)
a₃ – a₂ = a³ – a² = a²(a – 1)
a₄ – a₃ = a⁴ – a³ = a³(a – 1)
दो क्रमागत पदों का अन्तर नियत नहीं है।
अतः दिया गया अनुक्रम एक A.P. में नहीं है।

(xii) दिया हुआ अनुक्रम : √2, √8, √18, √32,……
a₁ = √2, a₂ = √8, a₃ = √18, a₄ = √32
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = √8 – √2 = √2(√4 – 1) = √2(2 – 1) = √2
a₃ – a₂ = √18 – √8 = √2(√9 – √4) = √2(3 – 2) = √2
a₄ – a₃ = √32 – √18 = √2(√16 – √9) = √2(4 – 3) = √2
दो क्रमागत पदों का अन्तर नियत (√2) है।
अत: सार्वान्तर (d) = √2 और दिया गया अनुक्रम एक A.P. में है।
तब, पाँचवाँ पद (a₅) = चौथा पद (a₄) + सार्वान्तर (d)
= √32 + √2
= √2(√16 + 1)
= √2(4 + 1)
= 5√2
= √25 × √2
= √50
छठाँ पद (a₆) = पाँचवाँ पद (a₅) + सार्वान्तर (d)
= √50 + √2
= √2 (√25 + 1)
= √2(5 + 1)
= 6√2
= √36 × √2
= √72
सातवाँ पद (a₇) = छठाँ पद (a₆) + सार्वान्तर (d)
= √72 + √2
= √2(√36 + 1)
= √2(6 + 1)
= 7√2
= √49 × √2
= √98
अत: दिए गए अनुक्रम के अगले तीन पद : √50, √72, √98 होंगे।

(xiii) दिया हुआ अनुक्रम : √3, √6, √9, √12,…..
a₁ = √3, a₂ = √6, a₃ = √9, a₄ = √12
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = √6 – √3 = √3(√2 – 1)
a₃ – a₂ = √9 – √6 = √3(√3 – √2)
a₄ – a₃ = √12 – √9 = 2√3 – 3
दो क्रमागत पदों का अन्तर नियत नहीं है।
अत: दिया गया अनुक्रम एक A.P. में नहीं है।

(xiv) दिया हुआ अनुक्रम : 1², 3², 5², 7²,…..
a₁ = 1², a₂ = 3², a₃ = 5², a₄ = 7²
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = 3² – 1² = 9 – 1 = 8
a₃ – a₂ = 5² – 3² = 25 – 9 = 16
a₄ – a₃ = 7² – 5² = 49 – 25 = 24
दो क्रमागत पदों का अन्तर नियत नहीं है।
अत: दिया गया अनुक्रम एक A.P. में नहीं है।

(xv) दिया हुआ अनुक्रम : 1², 5², 7², 73, ……
a₁ = 1², a₂ = 5², a₃ = 7², a₄ = 73,
दो क्रमागत पदों का अन्तर,
a₂ – a₁ = 5² – 1² = 25 – 1 = 24
a₃ – a₂ = 7² – 5² = 49 – 25 = 24
a₄ – a₃ = 73 – 7² = 73 – 49 = 24
दो क्रमागत पदों का अन्तर नियत (24) है।
सार्वान्तर (d) = 24 और दिया गया अनुक्रम एक A.P. में है।
तब, पाँचवाँ पद = चौथा पद + सार्वान्तर (d) = 73 + 24 = 97
छठाँ पद = पाँचवाँ पद + सार्वान्तर (d) = 97 + 24 = 121 = (11)²
सातवाँ पद = छठा पद + सार्वान्तर (d) = (11)² + 24 = 121 + 24 = 145
अत: दिए गए अनुक्रम के अगले तीन पद : 97, 11², 145 होंगे।

प्रश्नावली 5.2

प्रश्न 1. निम्नलिखित सारणी में, रिक्त स्थानों को भरिए, जहाँ A.P. का प्रथम पद a, सार्वान्तर d और n वाँ पद a_n है:

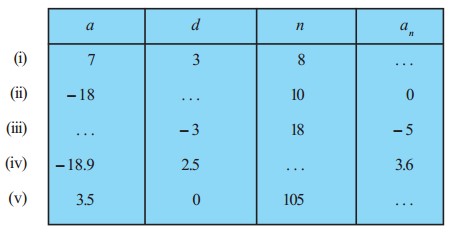
हल:
(i) दिया है, a = 7, d = 3, n = 8, a_n = ?
n वाँ पद (a_n) = a + (n – 1)d
= 7 + (8 – 1) × 3
= 7 + (7 × 3)
= 7 + 21
= 28
अत: an = 28

(ii) दिया है, a = -18, n = 10, a_n = 0, d = ?
n वाँ पद (a_n) = a + (n – 1)d
⇒ 0 = -18 + (10 – 1)d
⇒ -18 + 9d = 0
⇒ 9d = 18
⇒ d = 2
अतः d = 2

(iii) दिया है, d = -3, n = 18, a_n = -5, a = ?
n वाँ पद (a_n) = a + (n – 1)d
⇒ -5 = a + (18 – 1) × (-3)
⇒ -5 = a + (-51)
⇒ a = -5 + 51 = 46
अत: a = 46

(iv) दिया है, a = -18.9, d = 2.5, a_n = 3.6, n = ?
n वाँ पद (a_n) = a + (n – 1)d
⇒ 3.6 = -18.9 + (n – 1) (2.5)
⇒ 18.9 + 3.6 = (n – 1) (2.5)
⇒ (n – 1)(2.5) = 22.5
⇒ n – 1 = 9
⇒ n = 1 + 9 = 10
अतः n = 10

(v) दिया है, a = 3.5, d = 0, n = 10.5, a_n = ?
n वाँ पद (a_n) = a + (n – 1)d
= 3.5 + (10.5 – 1) (0)
= 3.5 + 0
= 3.5
अत: a_n = 3.5

प्रश्न 2. निम्नलिखित में सही उत्तर चुनिए और उसका औचित्य दीजिए :
(i) A.P.: 10, 7, 4,……, का 30 वाँ पद है :
(A) 97
(B) 77
(C) -77
(D) -87

प्रश्न 3. निम्नलिखित समान्तर श्रेढ़ियों में रिक्त खानों (boxes) के पदों को ज्ञात कीजिए :

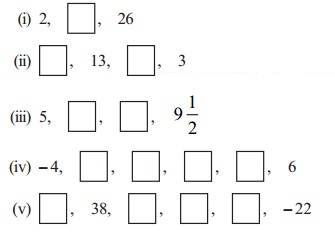
हल:
(i) पहला पद (a) = 2, तीसरा पद = 26, दूसरा पद = ?
माना सार्वान्तर (d) है,
तब, तीसरा पद (a₃) = a + 2d = 26
⇒ 2 + 2d = 26
⇒ 2d = 24
⇒ d = 12
दूसरा पद = a + d = 2 + 12 = 14
अत: रिक्त बॉक्स का पद (a₂) = 14

(iv) -4, a₂, a₃ , a₄, a₅, 6
पहला पद (a) = -4
माना सार्वान्तर d है।
तब, छठा पद = a + 5d
परन्तु छठा पद = 6
a + 5d = 6
⇒ -4 + 5d = 6
⇒ 5d = 10
⇒ d = 2
दूसरा पद (a₂) = a + d = -4 + 2 = -2
तीसरा पद (a₃) = a + 2d = -4 + 2 × 2 = -4 + 4 = 0
चौथा पद (a₄) = a + 3d = -4 + 3 × 2 = -4 + 6 = 2
पाँचवाँ पद (a₅) = a + 4d = -4 + 4 × 2 = -4 + 8 = 4
अत: बॉक्सों के रिक्त पद क्रमशः -2, 0, 2, 4 हैं।

(v) a, 38, a₃, a₄, a₅, -22
माना पहला पद (a) तथा सार्वान्तर (d) है।
तब, दूसरा पद = a + d
परन्तु a + d = 38 ……..(1)
और छठा पद = a + (6 – 1)d = a + 5d
परन्तु a + 5d = -22 ………(2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
(a + 5d) – (a + d) = -22 – 38
⇒ 4d = -60
⇒ d = -15
समीकरण (1) में d का मान रखने पर,
a + (-15) = 38
⇒ a = 38 + 15
⇒ a = 53
तीसरा पद (a₃) = a + 2d = 53 + 2(-15) = 53 – 30 = 23
चौथा पद (a₄) = a + 3d = 53 + 3(-15) = 53 – 45 = 8
पाँचवाँ पद (a₅) = a + 4d = 53 + 4(-15) = 53 – 60 = -7
अत: बॉक्सों के रिक्त पद क्रमशः 53, 23, 8, -7 हैं।

प्रश्न 4. A.P.: 3, 8, 13, 18, …… का कौन-सा पद 78 है?
हल:
दी गई A.P. : 3, 8, 13, 18, ……..
पहला पद (a) = 3 तथा सार्वान्तर (d) = 8 – 3 = 5
माना n वा पद (a_n) 78 है।
n वाँ पद (a_n) = 78
⇒ a + (n – 1)d = 78
⇒ 3 + (n – 1)5 = 78
⇒ 3 + 5n – 5 = 78
⇒ 5n = 78 + 5 – 3 = 80
⇒ n = 16
अत: 16 वाँ पद 78 है।

प्रश्न 5. निम्नलिखित समान्तर श्रेढ़ियों में से प्रत्येक श्रेढ़ी में कितने पद हैं?
(i) 7, 13, 19, ……, 205

हल:
(i) दी गई समान्तर श्रेढ़ी (A.P.) : 7, 13, 19, …… , 205
पहला पद (a) = 7 तथा सार्वान्तर (d) = 13 – 7 = 6
माना दी गई A.P. में n पद हैं जिसमें n वाँ पद (a_n) = 205
n वाँ पद (a_n) = 205
⇒ a + (n – 1)d = 205
⇒ 7 + (n – 1)6 = 205
⇒ 7 + 6n – 6 = 205
⇒ 6n = 205 + 6 – 7 = 204
⇒ n = 34
अतः दी गई श्रेढी (A.P.) में 34 पद हैं।

प्रश्न 6. क्या A.P. : 11, 8, 5, 2 का एक पद -150 है? क्यों?
हल:
दी गई A.P. : 11, 8, 5, 2
पहला पद (a) = 11 तथा सार्वान्तर (d) = 8 – 11 = -3
माना n वाँ पद (a_n) = -150 है।
n वाँ पद (a_n) = -150
⇒ a + (n – 1)d = -150
⇒ 11 + (n – 1) × -3 = -150
⇒ -3(n – 1) = -150 – 11 = -161
⇒ (n – 1) = 53.6 (लगभग)
⇒ n = 53.6 + 1 = 54.6
n का मान एक पूर्ण संख्या नहीं है।
अतः दी गई A.P. का कोई पद -150 नहीं है।

प्रश्न 7. उस A.P. का 31 वाँ पद ज्ञात कीजिए, जिसका 11 वाँ पद 38 है और 16 वाँ पद 73 है।
हल:
माना A.P. का पहला पद (a) तथा सार्वान्तर (d) है।
दिया है, A.P. का 11 वाँ पद (a₁₁) = 38
⇒ a + (n – 1)d = 38
⇒ a + (11 – 1)d = 38
⇒ a + 10d = 38 ………(1)
पुनः दिया है, A.P. का 16 वाँ पद (a₁₆) = 73
⇒ a + (16 – 1)d = 73
⇒ a + 15d = 73 ……..(2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
(a + 15d) – (a + 10d) = 73 – 38
⇒ 5d = 35
⇒ d = 7
समीकरण (1) में d का मान रखने पर,
a + 10 × 7 = 38
⇒ a + 70 = 38
⇒ a = 38 – 70 = -32
श्रेढ़ी का 31 वाँ पद (a₃₁) = a + (31 – 1)d
= -32 + 30 × 7
= -32 + 210
= 178
अतः A.P. का 31 वाँ पद = 178

प्रश्न 8. एक A.P. में 50 पद हैं, जिसका तीसरा पद 12 है और अन्तिम पद 106 है। इसका 29 वाँ पद ज्ञात कीजिए।
हल:
माना A.P. का प्रथम पद (a) तथा सार्वान्तर (d) है।
तब, तीसरा पद = a + (3 – 1)d = a + 2d
और अन्तिम 50 वाँ पद = a + (50 – 1)d = a + 49d
तब प्रश्नानुसार,
a + 2d = 12 ………(1)
a + 49d = 106 ……(2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
(a + 49d) – (a + 2d) = 106 – 12
⇒ 47d = 94
⇒ d = 2
तब समीकरण (1) में d का मान रखने पर,
a + 2 × 2 = 12
⇒ a + 4 = 12
⇒ a = 8
A.P. का 29 वाँ पद = a + (29 – 1)d
= 8 + 28 × 2
= 8 + 56
= 64
अतः दी गई A.P. का 29 वाँ पद 64 है।

प्रश्न 9. यदि किसी A.P. के तीसरे और नौवें पद क्रमशः 4 और -8 हैं तो इसका कौन-सा पद शून्य होगा?
हल:
माना श्रेढ़ी का पहला पद (a) तथा सार्वान्तर (d) है।
A.P. का तीसरा पद (a₃) = a + 2d
तथा नौवाँ पद (a₉) = a + (9 – 1) d = a + 8d
तब प्रश्नानुसार,
a + 2d = 4 ……(1)
a + 8d = -8 ……(2)
समीकण (2) में से समीकरण (1) को घटाने पर,
(a + 8d) – (a + 2d) = -8 – 4
या 6d = -12
या d = -2
समीकरण (1) में d का मान रखने पर,
a + 2 x (-2) = 4
⇒ a – 4 = 4
⇒ a = 8
माना श्रेढ़ी का n वाँ पद शून्य होगा, अर्थात्
a_n = 0
n वाँ पद (a_n) = 0
⇒ a + (n – 1)d = 0
⇒ 8 + (n – 1) × (-2) = 0
⇒ -2(n – 1) = -8
⇒ (n – 1) = 4
⇒ n = 5
अतः दी गई A.P. का 5 वाँ पद शून्य होगा।

प्रश्न 10. किसी A.P. का 17 वाँ पद उसके 10 वें पद से 7 अधिक है। इसका सार्वान्तर ज्ञात कीजिए।
हल:
माना A.P. का पहला पद (a) तथा सार्वान्तर (d) है।
तब, 17 वाँ पद (a₁₇) = a + (17 – 1)d = a + 16d
10 वा पद (a₁₀) = a + (10 – 1)d = a + 9d
प्रश्नानुसार, 17 वाँ पद, 10 वें पद से 7 अधिक है।
17 वाँ पद (a₁₇) – 10 वाँ पद (a₁₀) = 7
⇒ (a + 16d) – (a + 9d) = 7
⇒ 7d = 7
⇒ d = 1
अत: श्रेढ़ी का सार्वान्तर (d) = 1

प्रश्न 11. A.P. : 3, 15, 27, 39, ….. का कौन-सा पद उसके 54 वें पद से 132 अधिक होगा?
हल:
माना अभीष्ट पद n वाँ पद है।
दी गई A.P. : 3, 15, 27, 39, …..
प्रथम पद (a) = 3 तथा सार्वान्तर (d) = 15 – 3 = 12
तब, श्रेढ़ी का 54 वाँ पद (a₅₄) = a + (54 – 1)d
= 3 + (53 × 12)
= 3 + 636
= 639
n वॉ पद (a_n) = 54 वें पद से 132 अधिक
= 639 + 132
= 771
n वाँ पद (a_n) = 771
a + (n – 1)d = 771
3 + (n – 1) 12 = 771
(n – 1)12 = 771 – 3 = 768
n – 1 = 64
n = 64 + 1 = 65
अतः श्रेढ़ी का 65 वाँ पद 54 वें पद से 132 अधिक है।

प्रश्न 12. दो समान्तर श्रेढ़ियों का सार्वान्तर समान है। यदि इनके 100 वें पदों का अन्तर 100 है, तो इनके 1000 वें पदों का अन्तर क्या होगा?
हल:
माना पहली A.P. का पहला पद a तथा सार्वान्तर d है और दूसरी A.P. का पहला पद A तथा सार्वान्तर d है क्योंकि सार्वान्तर समान है।
तब, पहली श्रेढ़ी का 100 वाँ पद = a + (100 – 1)d = a + 99d
दूसरी श्रेढ़ी का 100 वा पद = A + (100 – 1) d = A + 99d
दोनों श्रेढ़ियों के 100 वें पदों का अन्तर = (A + 99d) – (a + 99d) = A – a
तब, प्रश्नानुसार, A – a = 100 ……(1)
अब, पहली श्रेढ़ी का 1000 वाँ पद = a + (1000 – 1)d = a + 999d
दूसरी श्रेढ़ी का 1000 वाँ पद = A + (1000 – 1)d = A + 999d
दोनों श्रेढ़ियों के 1000 वें पदों का अन्तर = (A + 999d) – (a + 999d) = A – a
दोनों श्रेढ़ियों के 1000 वें पदों का अन्तर = A – a = 100 [समीकरण (1) से]
अत: 1000 वें पदों का अन्तर = 100

प्रश्न 13. तीन अंकों वाली कितनी संख्याएँ 7 से विभाज्य हैं?
हल:
तीन अंकों की संख्याओं की सूची : 100, 101, 102, ……., 999
3 अंकों की 7 से विभाज्य पहली संख्या = 105
और अन्तिम संख्या = 994
तब, 7 से विभाज्य 3 अंकीय संख्याओं की सूची :
105, (105 + 7), (105 + 7 + 7), ……….., 994
= 105, 112, 119,…….,994
माना कुल संख्याएँ n हैं।
पहली संख्या (a) = 105, सार्वान्तर (d) = 7, n वाँ पद (a_n) = 994
n वा पद (a_n) = 994
a + (n – 1)d = 994
105 + (n – 1) × 7 = 994
(n – 1) × 7 = 994 – 105 = 889
(n – 1) = 889/7 = 127
n = 127 + 1 = 128
अतः 7 से विभाज्य तीन अंकीय संख्याएँ 128 हैं।

प्रश्न 14. 10 और 250 के बीच में 4 के कितने गणज हैं?
हल:
10 से बड़ा 4 का पहला गुणज = 12
250 से छोटा 4 का पहला गुणज = 248
10 और 250 के बीच 4 के गुणजों की सूची :
12, 12 + 4, (12 + 4 + 4),……., 248
12, 16, 20, 24, …….., 248.
माना गुणजों की संख्या n है।
यहाँ, पहला पद (a) = 12, सार्वान्तर (d) = 16 – 12 = 4
n वा पद (a_n) = 248
⇒ a + (n – 1)d = 248
⇒ 12 + (n -1) 4 = 248
⇒ 12 + 4n – 4 = 248
⇒ 4n = 248 + 4 – 12 = 240
⇒ n = 60
अत: 10 और 250 के बीच 4 के गुणजों की संख्या = 60

प्रश्न 15. n के किस मान के लिए, दोनों समान्तर श्रेढ़ियों 63, 65, 67, ….. और 3, 10, 17,…..के n वें पद बराबर होंगे?
हल:
पहली समान्तर श्रेढ़ी : 63, 65, 67,……
पहला पद (a) = 63, सार्वान्तर (d) = 65 – 63 = 2
श्रेढ़ी का n वा पद = a + (n – 1)d
= 63 + (n – 1)2
= 63 + 2n – 2
= 61 + 2n
दूसरी समान्तर श्रेढ़ी : 3, 10, 17, ……
पहला पद (A) = 3 सार्वान्तर (D) = 10 – 3 = 7
श्रेढ़ी का n वाँ पद = A + (n – 1)D
= 3 + (n – 1)7
= 3 + 7 n – 7
= 7n – 4
दोनों श्रेढ़ियों के n वें पद बराबर हैं।
7n – 4 = 61 + 2n
⇒ 7n – 2n = 61 + 4
⇒ 5n = 65
⇒ n = 13
अतः दी गई दोनों श्रेढ़ियों के 13 वें पद समान हैं।

प्रश्न 16. वह A.P. ज्ञात कीजिए जिसका तीसरा पद 16 है और 7 वाँ पद 5 वें पद से 12 अधिक है।
हल:
माना पहला पद a है तथा सार्वान्तर d है।
दिया है, A.P. का तीसरा पद = 16
a + 2d = 16 ……(1)
श्रेढ़ी का 7 वाँ पद (a₇) = a + (7 – 1)d = a + 6d
तथा 5 वाँ पद (a₅) = a + (5 – 1)d = a + 4d
7 वाँ पद 5 वें पद से 12 अधिक है
(a + 6d) – (a + 4d) = 12
⇒ a + 6d – a – 4d = 12
⇒ 2d = 12
⇒ d = 6
d का मान समीकरण (1) में रखने पर,
a + 2 × 6 = 16
⇒ a = 4
श्रेढ़ी का पहला पद (a) = 4
दूसरा पद (a₂) = a + d = 4 + 6 = 10
तीसरा पद (a₃) = a + 2d = 4 + 2 × 6 = 4 + 12 = 16
चौथा पद (a₄) = a + 3d = 4 + 3 × 6 = 4 + 18 = 22
अत: अभीष्ट A.P. : 4, 10, 16, 22, …….. है।

प्रश्न 17. A.P. : 3, 8, 13, ….., 253 में अन्तिम पद से 20 वाँ पद ज्ञात कीजिए।
हल:
दी गई A.P. : 3, 8, 13, ………, 253
पहला पद (a) = 3, सार्वान्तर (d) = 8 – 3 = 5
यदि श्रेढ़ी को अवरोही क्रम में लिखें तो यह निम्नवत् होगी
253, (253 – 5), (253 – 10), (253 – 15), ……., 3
या 253, 248, 243, 238, ………, 3
पहला पद (a) = 253 तथा सार्वान्तर (d) = 248 – 253 = -5
श्रेढ़ी का 20 वाँ पद = a + (20 – 1)d
= 253 + 19 × (-5)
= 253 – 95
= 158
अतः दी गई A.P. के अन्तिम पद से 20 वाँ पद = 158
वैकल्पिक विधिः A.P. का अन्त से n वाँ पद = l – (n – 1)d
जहाँ, पर l = अन्तिम पद यहाँ, l = 253, d = 8 – 3 = 5, n = 20
A.P. का अन्त से 20वाँ पद = 253 – (20 – 1) (5)
= 253 – 19 × 5
= 253 – 95
= 158

प्रश्न 18. किसी A.P. के चौथे और 8 वें पदों का योग 24 है तथा छठे और 10 वें पदों का योग 44 है। इस A.P. के प्रथम तीन पद ज्ञात कीजिए।
हल:
माना A.P. का पहला पद a तथा सार्वान्तर d है।
प्रश्नानुसार, 4वाँ पद (a₄) + 8 वाँ पद (a₈) = 24
⇒ a + (4 – 1)d + a + (8 – 1)d = 24
⇒ a + 3d + a + 7d = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12 ……..(1)
तथा 6वाँ पद (a₆) + 10वाँ पद (a₁₀) = 44
⇒ a + (6 – 1)d + a + (10 – 1)d = 44
⇒ a + 5d + a + 9d = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22 ……..(2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
(a +7d) – (a + 5d) = 22 – 12
⇒ 2d = 10
⇒ d = 5
d का यह मान समीकरण (1) में रखने पर,
a + 5 × 5 = 12
⇒ a + 25 = 12
⇒ a = -13
तब, श्रेढ़ी का पहला पद (a₁) = -13
दूसरा पद (a₂) = a + d = -13 + 5 = -8
तीसरा पद (a₃) = a + 2d = -13 + 2 × 5 = -13 + 10 = -3
अतः दी गई A.P. के प्रथम तीन पद = -13, -8, -3

प्रश्न 19. सुब्बाराव ने 1995 में ₹ 5000 के मासिक वेतन पर कार्य आरम्भ किया और प्रत्येक वर्ष ₹ 200 की वेतन वृद्धि प्राप्त की। किस वर्ष में उसका वेतन ₹ 7000 हो गया?
हल:
पहले वर्ष में प्रारम्भिक वेतन = ₹ 5000 प्रतिमास
दूसरे वर्ष में वेतन = ₹ (5000 + 200) = ₹ 5200
प्रतिमास तीसरे वर्ष में वेतन = ₹ (5200 + 200) = ₹ 5400 प्रतिमास
इस प्रकार प्रत्येक वर्ष के वेतन (₹)
5000, 5200, 5400, …….. एक समान्तर श्रेढ़ी बनाते हैं।
जिसका पहला पद (a) = 5000 तथा सार्वान्तर (d) = 200
माना n वर्ष बाद वेतन ₹ 7000 होगा।
तब, n वाँ पद = 7000
a + (n – 1)d = 7000
⇒ 5000 + (n – 1) 200 = 7000
⇒ (n – 1) × 200 = 7000 – 5000
⇒ (n – 1) × 200 = 2000
⇒ (n – 1) = 10
⇒ n = 10 + 1 = 11
अत: 11 वें वर्ष में सुब्बाराव का वेतन ₹ 7000 हो जायेगा।

प्रश्न 20. रामकली ने किसी वर्ष के प्रथम सप्ताह में ₹ 5 की बचत की और फिर अपनी साप्ताहिक बचत ₹ 1.75 बढ़ाती गई। यदि n वें सप्ताह में उसकी साप्ताहिक बचत ₹ 20.75 हो जाती है, तो n ज्ञात कीजिए।
हल:
प्रथम सप्ताह की बचत = ₹ 5
प्रत्येक सप्ताह की बचत में उत्तरोत्तर ₹ 1.75 की वृद्धि होती है।
प्रत्येक सप्ताह की बचतें एक A.P. का निर्माण करती हैं जिसका पहला पद (a) = 5 तथा सार्वान्तर (d) = ₹ 1.75
n वें सप्ताह में बचत = 20.75
a + (n – 1)d = 20.75
⇒ 5 + (n – 1) 1.75 = 20.75
⇒ (n – 1) × 1.75 = 20.75 – 5
⇒ (n – 1) × 1.75 = 15.75
⇒ n – 1 = 9
⇒ n = 9 + 1 = 10
अत: n = 10

प्रश्नावली 5.3

प्रश्न 1. निम्नलिखित समांतर श्रेढियों का योग ज्ञात कीजिए :
(i) 2, 7, 12, . . ., 10 पदों तक
(ii) -37, -33, -29, . . ., 12 पदों तक
(iii) 0.6, 1.7, 2.8, . . ., 100 पदों तक
(iv) , , , ……., 11 पदों तक
हल:
(i) दी गई समान्तर श्रेढ़ी : 2, 7, 12, …….., 10 पदों तक
पहला पद (a) = 2, सार्वान्तर (d) = 7 – 2 = 5, पदों की संख्या (n) = 10
n पदों का योग, S_n = n/2 [2a + (n – 1)d]
10 पदों तक योग, S₁₀ = 10/2 [2 × 2 + (10 – 1)5]
= 5[4 + (9 × 5)]
= 5[4 + 45]
= 5 × 49
= 245
अत: 10 पदों तक का योग = 245

(ii) दी गई समान्तर श्रेढ़ी : -37, -33, -29, ….., 12 पदों तक
पहला पद (a) = -37, सार्वान्तर (d) = (-33) – (-37) = -33 + 37 = 4,
पदों की संख्या (n) = 12
पदों का योग, S_n = n/2 [2a + (n – 1)d]
12 पदों का योग, S₁₂ = 12/2 [(2 × -37) + (12 – 1) × 4]
= 6[-74 + (11 × 4)]
= 6[-74 + 44]
= 6 × (-30)
= -180
अत: 12 पदों तक का योग = -180

(iii) दी गई समान्तर श्रेढ़ी : 0.6, 1.7, 2.8, …… , 100 पदों तक
पहला पद (a) = 0.6, सार्वान्तर (d) = 1.7 – 0.6 = 1.1, पदों की संख्या (n) = 100
पदों तक योग, S_n = n/2 [2a + (n – 1)d]
100 पदों तक योग, S₁₀₀ = 100/2 [(2 × 0.6) + (100 – 1) × 1.1]
= 50[1.2 + 99 × 1.1]
= 50[1.2 + 108.9]
= 50 × 110.1
= 5505
अत: 100 पदों तक का योग = 5505

प्रश्न 2. नीचे दिए हुए योग्फालों को ज्ञात कीजिये:
(i) 7 + 10+ 14 + ….. + 10
(ii) 34 + 32 + 30 + . . . + 10
(iii) -5 + (-8) + (-11) + . . . + (-230)
हल:

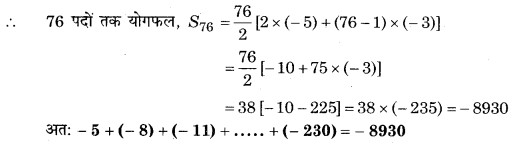
प्रश्न 3. एक A.P. में,
(i) a = 5, d = 3 और a_n = 50 दिया है। n और S_n ज्ञात कीजिए।
(ii) a = 7 और a₁₃ = 35 दिया है। d और S₁₃ ज्ञात कीजिए।
(iii) a₁₂ = 37 और d = 3 दिया है। n और S₁₂ ज्ञात कीजिए।
(iv) a₃ = 15 और S₁₀ = 125 दिया है। d और a₁₀ ज्ञात कीजिए।
(v) d = 5 और S₉ = 75 दिया है। a और a₉ ज्ञात कीजिए।
(vi) a = 2, d = 8 और S_n = 90 दिया है। n और a_n ज्ञात कीजिए।
(vii) a = 8, a_n = 62 और S_n = 210 दिया है। n और d ज्ञात कीजिए।
(viii) a_n = 4, d = 2 और S_n = -14 दिया है। n और a ज्ञात कीजिए।
(ix) a = 3, n = 8 और S = 192 दिया है। d ज्ञात कीजिए।
(x) l = 28, S = 144 और कुल 9 पद हैं। a ज्ञात कीजिए।
हल:
(i) दिया है, a = 5, d = 3 और a_n = 50
अनुक्रम A.P. में है और a_n = 50
a + (n – 1)d = 50
⇒ 5 + (n – 1) 3 = 50
⇒ 5 + 3n – 3 = 50
⇒ 3n = 50 + 3 – 5
⇒ 3n = 48
⇒ n = 16
सूत्र S_n = n/2 [2a + (n – 1) d] से,
S₁₆ = 16/2 [(2 × 5) + (16 – 1) × 3]
= 8 [10 + (15 × 3)]
= 8 [10 + 45]
= 8 × 55
= 440
अत: n = 16 तथा S_n = 440

(ii) दिया है, a = 7 और a₁₃ = 35
यहाँ, a₁₃ = 35

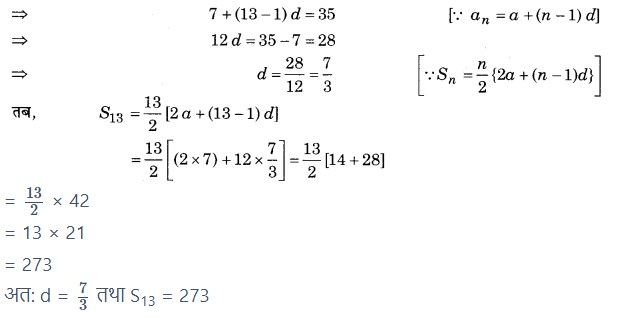
(iii) दिया है, a₁₂ = 37 और d = 3
यहाँ, a₁₂ = 37
⇒ a + (12 – 1)d = 37
⇒ a + 11d = 37
⇒ a + 11 x 3 = 37
⇒ a + 33 = 37
⇒ a = 4
तब, S₁₂ = 12/2 [2a + (12 – 1)d]
= 6 [(2 × 4) + 11 × 3]
= 6[8 + 33]
= 6 × 41
= 246
अत: a = 4 तथा S₁₂ = 246

(iv) दिया है, a₃ = 15 और S₁₀ = 125
a₃ = 15
a + (3 – 1)d = 15
a + 2d = 15 …… (1)
और S₁₀ = 125

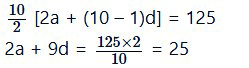
2a + 9d = 25 …….(2)
समीकरण (1) को 2 से गुणा करके समीकरण (2) में से घटाने पर,
(2a + 9d) – (2a + 4d) = 25 – 30
5d = -5
d = -1
समीकरण (1) में d का मान रखने पर,
a + 2(-1) = 15
a = 15 + 2 = 17
a10 = a + (10 – 1)d
= 17 + 9 × (-1)
= 17 – 9
= 8
a₁₀ = 8
अतः d = -1 और a₁₀ = 8

(v) दिया है, d = 5 और S₉ = 75
S₉ = 9/2 [2a + (9 – 1)d]
= 9/2 [2a + 8d]
= 9a + 36d
= 9(a + 4d)
परन्तु S₉ = 75 दिया है
9(a + 4d) = 75

(viii) दिया है, a_n = 4, d = 2 और S_n = -14
यहाँ, a_n = 4
⇒ a + (n – 1)d = 4
⇒ a + (n – 1)2 = 4
⇒ a + 2n – 2 = 4
⇒ a + 2n = 6 ……..(1)
S_n = -14
n/2 [2a + (n – 1) 2] = -14
⇒ n[a + n – 1] = -14 ……..(2)
समीकरण (1) से, a = 6 – 2n
तब, समीकरण (2) में a का मान रखने पर,
n(6 – 2n + n – 1) = -14
⇒ n(5 – n) = -14
⇒ 5n – n² = -14
⇒ n² – 5n – 14 = 0
⇒ n² – 7n + 2n – 14 = 0
⇒ n(n – 7) + 2 (n – 7) = 0
⇒ (n – 7) (n + 2) = 0
⇒ n = 7 या n = -2
n एक धन पूर्णांक होना चाहिए।
n = 7
तब, a = 6 – 2n = 6 – (2 × 7) = 6 – 14 = -8
a = -8 तथा n = 7

(ix) दिया है, a = 3, n = 8 और S_n = 192
S_n = n/2 [2a + (n – 1) d] से,
⇒ n/2 [2a + (n – 1)d] = 192 [∵ S = 192, दिया है]
⇒ 8/2 [(2 × 3) + (8 – 1) d] = 192
⇒ 4[6 + 7d] = 192
⇒ 24 + 28d = 192
⇒ 28d = 192 – 24 = 168
⇒ d = 6
अत: d = 6

(x) दिया है, अन्तिम पद, l = 28, S = 144 और कुल पद = 9
सूत्र, S = n/2 [a + l] से,
⇒ 144 = 9/2 [a + 28]
⇒ 288 = 9[a + 28]
⇒ 288 = 9a + 252
⇒ 9a = 288 – 252
⇒ 9a = 36
⇒ a = 4
अतः a = 4

प्रश्न 4. 636 योग प्राप्त करने के लिए A.P.: 9, 17, 25,….. के कितने पद लेने चाहिए?
हल:
दी गई A.P. : 9, 17, 25, ……..
यहाँ a = 9 तथा d = 17 – 9 = 8
माना पदों की संख्या n है। .
S_n = 636 (दिया है)

परन्तु n एक धन पूर्णांक होना चाहिए।
n = 12
अत: 12 पद लेने चाहिए।

प्रश्न 5. किसी A.P. का प्रथम पद 5, अन्तिम पद 45 और योग 400 है। पदों की संख्या और सार्वान्तर ज्ञात कीजिए।
हल:
दिया है, प्रथम पद (a) = 5, अन्तिम पद (l) = 45 योग (S) = 400
माना पदों की संख्या n है।
सूत्र, S = n/2 (a + l) से,
400 = n/2 [5 + 45]
400 = n/2 × 50
25n = 400
n = 16
अन्तिम पद (l) = 45 परन्तु 16 वाँ पद भी अन्तिम पद है।
a₁₆ = 45
a + (16 – 1)d = 45
5 + 15d = 45
15d = 45 – 5 = 40
d = 40/15 = 8/3
अतः पदों की संख्या n = 16 तथा सार्वान्तर = 8/3

प्रश्न 6. किसी A.P. के प्रथम और अन्तिम पद क्रमशः 17 और 350 हैं। यदि सार्वान्तर 9 है तो इसमें कितने पद हैं और इनका योग क्या है?
हल:
दिया है, प्रथम पद (a) = 17 अन्तिम पद (l) = 350 तथा सार्वान्तर (d) = 9
माना दी गई A.P. में पदों की संख्या n हैं।
तब, अन्तिम पद, l = n वाँ पद
l = a + (n – 1)d
350 = 17 + (n – 1)9
350 – 17 = 9n – 9
350 – 17 + 9 = 9n
9n = 342
n = 38
तब, 38 पदों का योग, S38 = n/2 (a + l)
= 38/2 (17 + 350)
= 19 × 367
= 6973
अतः पदों की संख्या = 38 तथा पदों का योग = 6973

प्रश्न 7. उस A.P. के प्रथम 22 पदों का योग ज्ञात कीजिए, जिसमें d = 7 है और 22 वाँ पद 149 है।
हल:
दिया है, d = 7 तथा n = 22
22 वाँ पद = 149
a₂₂ = a + (22 – 1)d = 149
a + 21 × 7 = 149
a + 147 = 149
a = 2
तब, प्रथम 22 पदों का योग, S₂₂ = n/2 (a + a₂₂)
= 22/2 (2 + 149)
= 11 × 151
= 1661
अत: दी गई A.P. के प्रथम 22 पदों का योग = 1661

प्रश्न 8. उस A.P. के प्रथम 51 पदों का योग ज्ञात कीजिए, जिसके दूसरे और तीसरे पद क्रमश: 14 और 18 हैं।
हल:
दिया है, A.P. का दूसरा पद (a₂) = 14
तीसरा पद (a₃) = 18
सार्वान्तर (d) = a₃ – a₂ = 18 – 14 = 4
अब पुनः दूसरा पद = 14
a + d = 14
a + 4 = 14 [∵ d = 4]
a = 14 – 4
a = 10
तब, सूत्र S_n = n/2 [2a + (n – 1)d] से,
51 पदों का योग, S₅₁ = 51/2 [2 × 10 + (51 – 1) 4] [∵ n = 51]
= 51/2 [20 + (50 × 4)]
= 51/2 [20 + 200]
= 51/2 × 220
= 51 x 110
= 5610
अत: दी गई A.P. के प्रथम 51 पदों का योग 5610 है।

प्रश्न 9. यदि किसी A.P. के प्रथम 7 पदों का योग 49 है और प्रथम 17 पदों का योग 289 है, तो इसके प्रथम n पदों का योग ज्ञात कीजिए।
हल:
माना A.P. का पहला पद a तथा सार्वान्तर d है।
दिया है, प्रथम 7 पदों का योग (S₇) = 49
7/2 [2a + (7 – 1) d] = 49
7/2 [2a + 6d] = 49
7(a +3d) = 49
a + 3d = 7 ……..(1)
इसी प्रकार, प्रथम 17 पदों का योग = 289
17/2 [2a + (17 – 1) d] = 289
17/2 [2a + 16d] = 289
17/2 × 2[a + 8d] = 289
a + 8d = 17 …….(2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
a + 8d – (a + 3d) = 17 – 7
5d = 10
d = 2
समीकरण (1) में d का मान रखने पर,
a + 3 × 2 = 7
a + 6 = 7
a = 1
a = 1, तथा d = 2
तब, प्रथम n पदों का योग, S_n = n/2 [2a + (n – 1)d]
= n/2 [2 × 1 + (n – 1)2]
= n/2 [2 + (n – 1)2]
= n/2 [2 + 2n – 2]
= n/2 (2n)
= n²
अत: प्रथम n पदों का योग = n²

प्रश्न 10. दर्शाइए कि a₁, a₂,….., a_n,…..से एक A.P. बनती है, यदि a_n नीचे दिए अनुसार परिभाषित है :
(i) a_n = 3 + 4n
(ii) a_n = 9 – 5n
साथ ही, प्रत्येक स्थिति में, प्रथम 15 पदों का योग ज्ञात कीजिए।
हल:
(i) दिया है, किसी अनुक्रम का n वाँ पद (a_n) = 3 + 4n
n = 1 रखने पर, पहला पद (a₁) = 3 + 4(1) = 7
n = 2 रखने पर, दूसरा पद (a₂) = 3 + 4(2) = 11
n = 3 रखने पर, तीसरा पद (a₃) = 3 + 4(3) = 15
अत: अभीष्ट अनुक्रम = 7, 11, 15, ……,(3 + 4n) है।
सार्वान्तर = दूसरा पद (a₂) – पहला पद (a₁) = 11 – 7 = 4
अथवा तीसरा पद (a₃) – दूसरा पद (a₂) = 15 – 11 = 4
सार्वान्तर नियत है; अत: अनुक्रम एक A.P. है।
तब, प्रथम 15 पदों का योगफल,
अत: अनुक्रम = 7, 11, 15, …… , (3 + 4n) A.P. है तथा योगफल = 525

(ii) दिया है, अनुक्रम का n वा पद (a_n) = 9 – 5n
n = 1 रखने पर, पहला पद (a₁) = 9 – 5(1) = 4
n = 2 रखने पर, दूसरा पद (a₂) = 9 – 5(2) = -1
n = 3 रखने पर, तीसरा पद (a₃) = 9 – 5(3) = -6
अत: अनुक्रम 4, -1, -6,….., (9 – 5n) है।
पदों का सार्वान्तर (d) = दूसरा पद (a₂) – पहला पद (a₁) = -1 – (4) = -5
अथवा तीसरा पद (a₃) – दूसरा पद (a₂) = -6 – (-1) = -5
चूँकि सार्वान्तर नियत है; अत: अनुक्रम एक A.P. है।
तब, प्रथम 15 पदों का योगफल,

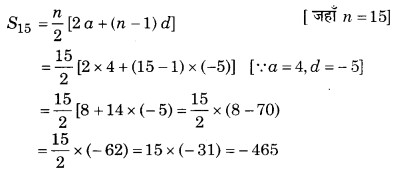
अत: अनुक्रम = 4, -1, -6,……,(9 – 5n) A.P. है तथा योगफल = -465

प्रश्न 11. यदि किसी A.P. के प्रथम n पदों का योग 4n – n² है, तो इसका प्रथम पद (अर्थात S₁) क्या है? प्रथम दो पदों का योग क्या है? दूसरा पद क्या है? इसी प्रकार, तीसरे, 10 वें और nवें पद ज्ञात कीजिए।
हल:
दिया है, A.P. के प्रथम n पदों का योगफल, S_n = 4n – n²
n = 1 रखने पर, S₁ = (4 × 1) – (1)² = 3
प्रथम पद (a₁) = 3
n = 2 रखने पर,
S2 = (4 × 2) – (2)² = 8 – 4 = 4
प्रथम दो पदों का योगफल, S₂ = 4
प्रथम पद (a₁) = 3
दूसरा पद (a₂) = S₂ – S₁ = 4 – 3 = 1
n = 3 रखने पर,
S₃ = 4n – n²
= (4 × 3) – (3)²
= 12 – 9
= 3
तीसरा पद (a₃) = S₃ – S₂ = 3 – 4 = -1
n = 9 रखने पर, S₉ = 4n – n² = 4 × 9 – 9² = 36 – 81 = -45
n = 10 रखने पर, S₁₀ = 4n – n² = 4 × 10 – 10² = 40 – 100 = -60
10 वाँ पद (a₁₀) = S₁₀ – S₉ = -60 – (-45) = -60 + 45 = -15
S_n = 4n – n² और S_n-1 = 4(n – 1) – (n – 1)² [n के स्थान पर (n – 1) रखने पर]
= (n – 1) [4 – (n – 1)]
= (n – 1)[4 – n + 1]
= (n – 1) (5 – n)
= 5n – n² – 5 + n
= 6n – n² – 5
n वाँ पद (a_n) = S_n – S_n-1
= (4n – n²) – (6n – n² – 5)
= 4n – n² – 6n + n² + 5
= 5 – 2n
अत: S₁ = 3, प्रथम दो पदों का योग, S₂ = 4, दूसरा पद, a₂ = 1, तीसरा पद,(a₃) = -1,
10 वाँ पद, a₁₀ = -15 तथा n वाँ पद, a_n = 5 – 2n

प्रश्न 12. ऐसे प्रथम 40 धन पूर्णांकों का योग ज्ञात कीजिए जो 6 से विभाज्य हो।
हल:
6 से विभाज्य धन पूर्णांक क्रमशः
6, 12, 18, 24, 30, …….., 40 पदों तक
पहला पद (a) = 6, सार्वान्तर (d) = 12 – 6 = 6, तथा n = 40
प्रथम n पदों का योगफल, S_n = n/2 [2a + (n – 1) d]
प्रथम 40 पदों का योगफल, S₄₀ = 40/2 [(2 × 6) + (40 – 1) 6]
= 20 [12 + 39 × 6]
= 20 [12 + 234]
= 20 × 246
= 4920
अत: 6 से विभाज्य प्रथम 40 धन पूर्णांकों का योग = 4920

प्रश्न 13. 8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
हल:
8 के प्रथम 15 गुणज क्रमश:
8, 16, 24, 32, ………., 15 पदों तक
S = 8 + 16 + 24 + 32 +…….+ 15 × 8
= 8[1 + 2 + 3 + 4 +……+ 15]
= 8[15/2 (1 + 15] [∵ S_n = n/2 [a + l]]
= 8[15/2 × 16]
= 8 × 120
= 960
अत: 8 के प्रथम 15 गुणजों का योगफल = 960

प्रश्न 14. 0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
हल:
0 और 50 के बीच की विषम संख्याएँ क्रमश:
1, 3, 5, 7, ……….., 49
यहाँ a = 1, d = 3 – 1 = 2, तथा a_n = 49
a_n = 49
a + (n – 1)d = 49
1 + (n – 1)2 = 49
(n – 1) 2 = 48
(n – 1) = 24
n = 25
A.P.: 1, 3, 5, 7, ………. का 25 पदों तक योगफल

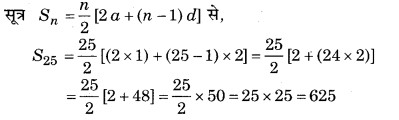
अतः शून्य और 50 के बीच की विषम संख्याओं का योगफल = 625

प्रश्न 15. निर्माण कार्य से सम्बन्धित किसी ठेके में, एक निश्चित तिथि के बाद कार्य को विलम्ब से पूरा करने के लिए, जुर्माना लगाने का प्रावधान इस प्रकार है : पहले दिन के लिए ₹ 200, दूसरे दिन के लिए ₹ 250, तीसरे दिन के लिए ₹ 300 इत्यादि, अर्थात् प्रत्येक उत्तरोत्तर दिन का जुर्माना अपने से ठीक पहले दिन के जुर्माने से ₹ 50 अधिक है। एक ठेकेदार को जुर्माने के रूप में कितनी राशि अदा करनी
पड़ेगी, यदि वह इस कार्य में 30 दिन का विलम्ब कर देता है?
हल:
यहाँ, पहले दिन के विलम्ब के लिए अर्थदण्ड = ₹ 200
दूसरे दिन के विलम्ब के लिए अर्थदण्ड = ₹ 250
तीसरे दिन के विलम्ब के लिए अर्थदण्ड = ₹ 300
………………………..
………………………..
a = 200, d = 250 – 200 = 50, तथा n = 30 दिन
30 दिन के विलम्ब के बाद अर्थदण्ड का योगफल,
S₃₀ = 30/2 [(2 × 200) + (30 – 1) × 50]
[∵ सूत्र, S_n = n/2 [2a + (n – 1)d] से]
= 15[400 + 29 × 50]
= 15[400 + 1450]
= 15 × 1850
= 27750
अत: ठेकेदार को जुर्माने के रूप में ₹ 27750 देने होंगे।

प्रश्न 16. किसी स्कूल के विद्यार्थियों को उनके समग्र शैक्षिक प्रदर्शन के लिए 7 नकद पुरस्कार देने के लिए ₹ 700 की राशि रखी गई है। यदि प्रत्येक पुरस्कार अपने से ठीक पहले पुरस्कार से ₹ 20 कम है, तो प्रत्येक पुरस्कार का मान ज्ञात कीजिए।
हल:
माना पहला पुरस्कार ₹ a है।
दूसरा पुरस्कार (a₂) = (a – 20)
तीसरा पुरस्कार (a₃) = ₹ (a – 20 – 20) = ₹ (a – 40)
चौथा पुरस्कार (a₄) = ₹ (a – 40 – 20) = ₹ (a – 60)
पाँचवाँ पुरस्कार (a₅) = ₹ (a – 60 – 20) = ₹ (a – 80)
छठा पुरस्कार (a₆) = ₹ (a – 80 – 20) = ₹ (a – 100)
सातवा पुरस्कार (a₇) = ₹ (a – 100 – 20) = ₹ (a – 120)
कुल पुरस्कारों की धनराशि = a + a₂ + a₃ + a₄ + a₅ + a₆ + a₇
= a + (a – 20) + (a – 40) + (a – 60) + (a – 80) + (a – 100) + (a – 120)
= 7a – 420
प्रश्नानुसार, यह धनराशि ₹ 700 है।
7a – 420 = 700
7a = 700 + 420
7a = 1120
a = 160
पहला पुरस्कार = ₹ 160, शेष पुरस्कार क्रम से ₹ 20 – 20 कम है।
अतः पुरस्कार ₹ 160, ₹ 140, ₹ 120, ₹ 100, ₹ 80, ₹ 60, ₹ 40 हैं।

प्रश्न 17. एक स्कूल के विद्यार्थियों ने वायु प्रदूषण कम करने के लिए स्कूल के अन्दर और बाहर पेड़ लगाने के बारे में सोचा। यह निर्णय लिया गया कि प्रत्येक कक्षा का प्रत्येक अनुभाग अपनी कक्षा की संख्या के बराबर पेड़ लगाएगा। उदाहरणार्थ, कक्षा I का एक अनुभाग 1पेड़ लगाएगा, कक्षा II का एक अनुभाग 2 पेड़ लगाएगा, कक्षा III का एक अनुभाग 3 पेड़ लगाएगा, इत्यादि और ऐसा कक्षा XII तक के लिए चलता रहेगा। प्रत्येक कक्षा के तीन अनुभाग हैं। इस स्कूल के विद्यार्थियों द्वारा लगाए गए कुल पेड़ों की संख्या कितनी होगी?
हल:
प्रत्येक कक्षा में तीन अनुभाग हैं।
कक्षा I द्वारा लगाए गए कुल पेड़ = 3 × 1 = 3
कक्षा II द्वारा लगाए गए कुल पेड़ = 3 × 2 = 6
कक्षा III द्वारा लगाए गए कुल पेड़ = 3 × 3 = 9
कक्षा IV द्वारा लगाए गए कुल पेड़ = 3 × 4 = 12
………………………..
………………………..
तब, अनुक्रम A.P. : 3, 6, 9, 12, ………. बनता है।
a = 3, तथा d = 6 – 3 = 3
तब, कक्षा XII तक के कुल विद्यार्थियों द्वारा लगाए गए पेड़ों का योगफल
सूत्र, S_n = n/2 [2a + (n – 1)d] से,
S₁₂ = 12/2 [(2 × 3) + (12 – 1) × 3]
= 6[6 + 33]
= 6 × 39
= 234
अत: स्कूल के विद्यार्थियों द्वारा लगाए कुल पेड़ = 234

प्रश्न 18. केंद्र A से प्रारंभ करते हुए, बारी-बारी से केन्द्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm …. वाले उत्तरोत्तर अर्धवृतों को खींचकर एक सर्पिल (spiral) बनाया गया है, जैसा कि आकृति में दर्शाया गया है| तेरह क्रमागत अर्धवृतों से बने इस सर्पिल की कुल लंबाई क्या है ? (π = ) लीजिए। [संकेत : क्रमशः केन्द्रों A, B, A, B… वाले अर्धवृत्तों की लम्बाइयाँ l1, l2, l3, l4 हैं।

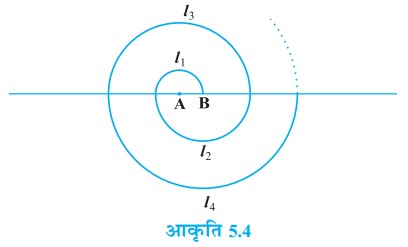
हल:
पहले अर्द्धवृत्त की त्रिज्या, r₁ = 0.5 cm
दूसरे अर्द्धवृत्त की त्रिज्या, r₂ = 1.0 cm
तीसरे अर्द्धवृत्त की त्रिज्या, r₃ = 1.5 cm
चौथे अर्द्धवृत्त की त्रिज्या, r₄ = 2.0 cm
……………………………….
……………………………….
13 वें अर्द्धवृत्त की त्रिज्या, r₁₃ = ?
r₁ = a = 0.5 cm, d = 1.0 – 0.5 = 0.5 cm तथा n = 13
r₁₃ = a + (n – 1) d = 0.5 + (13 – 1) × 0.5
= 0.5 + 12 × 0.5
= 0.5 + 6.0
= 6.5
अर्द्धवृत्तों की वृत्तीय परिधियाँ :
πr₁, πr₂, πr₃, ………., πr₁₃
13 क्रमागत अर्द्धवृत्तों से बने सर्पिल की लम्बाई

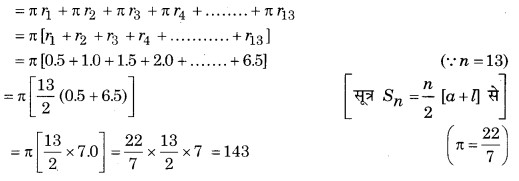
अत: सर्पिल की लम्बाई = 143 cm

प्रश्न 19. 200 लट्ठों (logs) को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में 20 लढे, उससे अगली पंक्ति में 19 लटे, उससे अगली पंक्ति में 18 लट्टे, इत्यादि जैसा कि चित्र में प्रदर्शित है। ये 200 लटे कितनी पंक्तियों में रखे हुए हैं तथा सबसे ऊपरी पंक्ति में कितने लढे हैं?

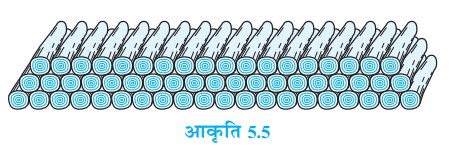
हल:
दिया है, सबसे निचली पंक्ति में 20 लटे हैं।
अर्थात् नीचे से प्रारम्भ कर प्रथम पंक्ति में = 20 लढे
दूसरी पंक्ति में = 19 लढे
तीसरी पंक्ति में = 18 लढे
चौथी पंक्ति में = 17 लढे ……… इत्यादि
तब, एक A.P. बनती है : 20, 19, 18, 17, …..
a = 20, तथा d = 19 – 20 = -1
माना पंक्तियों की संख्या n हैं।

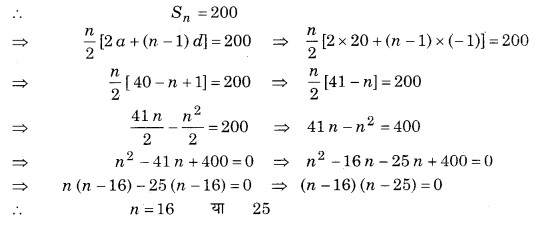
यदि n = 25, तो a_n = a + (n – 1)d
= 20 + (25 – 1) × (-1)
= 20 – 24
= -4
अत: n = 25 स्वीकार्य नहीं है।
तब, n = 16 से,
a_n = a + (n – 1) d
= 20 + (16 – 1) × -1
= 20 + (15 × (-1))
= 20 – 15
= 5
अत: कुल पंक्तियाँ = 16 और सबसे ऊपर की पंक्ति में लट्ठों की संख्या = 5

प्रश्न 20. एक आलू दौड़ (potato race) में, प्रारम्भिक स्थान पर एक बाल्टी रखी हुई है, जो पहले आलू से 5 मीटर की दूरी पर है तथा अन्य आलुओं को एक सीधी रेखा में परस्पर 3 m की दूरियों पर रखा गया है। इस रेखा पर 10 आलू रखे गए हैं। जैसा कि चित्र में दिखाया गया है।

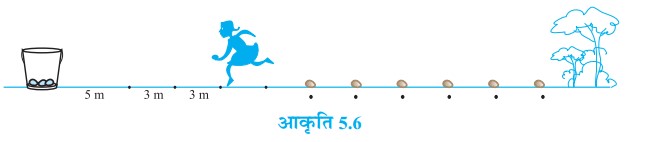
प्रत्येक प्रतियोगी बाल्टी से चलना प्रारम्भ करती है, निकटतम आलू को उठाती है, उसे लेकर वापस आकर दौड़कर बाल्टी में डालती है, दूसरा आलू उठाने के लिए वापस दौड़ती है, उसे उठाकर वापस बाल्टी में डालती है और वह ऐसा तब तक करती रहती है, जब तक सभी आलू बाल्टी में न आ जाएँ। इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी?
[संकेत : पहले और दूसरे आलुओं को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी = 2 × 5 + 2 × (5 + 3) है।]
हल:
पहले आलू की बाल्टी से दूरी = 5 m
दूसरे आलू की बाल्टी से दूरी = (5 + 3) = 8 m
तीसरे आलू की बाल्टी से दूरी = (8 + 3) = 11 m
चौथे आलू की बाल्टी से दूरी = (11 + 3) = 14 m
इस प्रकार बाल्टी से आलुओं की दूरी A.P. में है जिसका
पहला पद (a) = 5 m तथा सार्वान्तर (d) = 3 m
एक बार बाल्टी से चलकर आलू को उठाना होता है और उसे फिर वापस बाल्टी में डालना पड़ता है।
आलू बाल्टी में डालने के लिए चली दूरियाँ :
= 2 × 5 m, 2 × 8 m, 2 × 11 m, 2 × 14 m, …….
= 10 m, 16 m, 22 m, 28 m, …………
यहाँ a = 10, d = 16 – 10 = 6, तथा n = 10
n आलुओं को उठाकर बाल्टी में डालने के लिए चली दूरी = n/2 [2a + (n – 1)d]
10 आलुओं की रेस में चली दूरी = 10/2 [2 × 10 + (10 – 1) × 6]
= 5[20 + (9 × 6)]
= 5[20 + 54]
= 5[74]
= 370 m
अतः प्रतियोगी द्वारा चली दूरी = 370 m

प्रश्नावली 5.4

प्रश्न 1. A.P.: 121, 117, 113,…… का कौन-सा पद सबसे पहला ऋणात्मक पद होगा?
[संकेत : a_n < 0 के लिए n ज्ञात कीजिए।]
हल:
दी गई A.P.: 121, 117, 113, ………
प्रथम पद (a) = 121
तथा सार्वान्तर (d) = 117 – 121 = -4
मान लिया n वाँ पद प्रथम ऋणात्मक पद होगा।
a_n < 0
⇒ a + (n – 1)d < 0
⇒ 121 + (n – 1) × (-4) < 0
⇒ -(n – 1) 4 < -121
⇒ n – 1 < 121/4
⇒ n < 121/4 + 1
⇒ n < 125/4
⇒ n < 31.25
n < 32 क्योंकि n = एक पूर्णांक है।
अत: 32 वाँ पद पहला ऋणात्मक पद होगा।

प्रश्न 2. किसी A.P. के तीसरे और सातवें पदों का योग 6 है और उनका गणनफल 8 है। इस A.P. के प्रथम 16 पदों का योग ज्ञात कीजिए।
हल:
माना दी गई A.P. का पहला पद a तथा सार्वान्तर d है।
तीसरा पद (a₃) = a + (3 – 1)d = a + 2d
सातवाँ पद (a₇) = a + (7 – 1)d = a + 6d
प्रश्नानुसार, तीसरे + सातवें पद का योग = 6
⇒ a₃ + a₇ = 6
⇒ a + 2d + a + 6d = 6
⇒ 2a + 8d = 6
⇒ a + 4d = 3 ……(1)
पुनः प्रश्नानुसार,
a₃ × a₇ = 8
⇒ (a + 2d) × (a + 6d) = 8
⇒ a² + 8ad + 12d² = 8 ……..(2)
समीकरण (1) के वर्ग में से समीकरण (2) को घटाने पर,
(a + 4d)² – (a² + 8ad + 12d²) = (3)² – 8
⇒ a² + 8ad + 16d² – a² – 8ad – 12d² = 9 – 8
⇒ 4d² = 1

अतः प्रथम 16 पदों का योग = 20 अथवा 76

प्रश्न 3. एक सीढ़ी के क्रमागत डंडे परस्पर 25 cm की दुरी पर हैं| (देखिए आकृति 5.7)| डंडों की लंबाई एक समान रूप से घटती जाती है तथा सबसे निचले डंडे की लंबाई 45 cm है और सबसे ऊपर वाले डंडे की लंबाई 25 cm है | यदि ऊपरी और निचले डंडे के बीच की दुरी 2m है, तो डंडों को बनाने के लिए लकड़ी की कितनी लंबाई की आवश्यकता होगी ? [संकेत : डंडों की संख्या = ÷ 1 हैं|]

हल:
प्रथम व अन्तिम डण्डे के बीच की क्षैतिज दूरी

= 5.5 × 70 cm
= 385 cm
= 3.85 m
अत: सीढ़ी के डण्डों में प्रयुक्त लकड़ी की लम्बाई = 385 cm या 3.85 m

प्रश्न 4. एक पंक्ति के मकानों को क्रमागत रूप से संख्या 1 से 49 तक अंकित किया गया है। दर्शाइए कि x का एक ऐसा मान है कि x से अंकित मकान से पहले के मकानों की संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग के बराबर है। x का मान ज्ञात कीजिए।
[संकेत : S_x-1 = S₄₉ – S_x है]
हल:
दिया है, मकानों पर अंकित संख्याएँ : 1, 2, 3, 4, 5, 6, ……., 47, 48, 49 हैं।
x एक ऐसी संख्या है कि x के एक ओर की संख्याओं का योग = x के दूसरी ओर की संख्याओं का योग
अर्थात् 1 से x – 1 तक की संख्याओं का योग = x – 1 से 49 तक की सभी संख्याओं का योग
अनुक्रम की सभी संख्याओं में सार्वान्तर, d = 1
तब, 1 से x – 1 तक की संख्याओं का योग

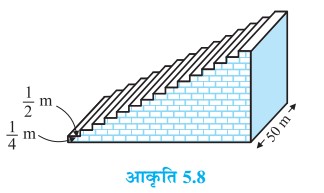
प्रश्न 5. एक फुटबॉल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीढीयाँ बनी हुई हैं| इन सीढीयों में से प्रत्येक की लंबाई 50m है वह ठोस कंक्रीट ( concrete) की बनी है प्रत्येक सीढ़ी में m की चौड़ाई है और m का फैलाव (चौड़ाई) है| (देखिए आकृति 5.8 )| इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए| [संकेत : पहली सीढ़ी को बनाने में लगी कंक्रीट का आयतन = x x 50 m³ है|]

हल:
दिया है, प्रत्येक सीढ़ी की लम्बाई 50m तथा चौड़ाई  m है।
सीढ़ियों की संख्या 15 है। प्रत्येक सीढ़ी की जमीन से ऊँचाई एक समान्तर श्रेढ़ी (A.P.) का अनुक्रम है जो निम्नवत् है :

अत: चबूतरे में लगी कंक्रीट का आयतन = 750 m³

समांतर श्रेढ़ियाँ Additional Questions

बहुविकल्पीय प्रश्न

प्रश्न 1.
किसी A.P. में, यदि d = -4, n = 7 और a_n = 4 है, तो a का मान है
(i) 6
(ii) 7
(iii) 20
(iv) 28
हल
(iv) 28

प्रश्न 2.
किसी A.P. में, यदि a = 3.5, d = 0 और n = 101 है, तो, a_n बराबर है
(i) 0
(ii) 3.5
(iii) 103.5
(iv) 104.5
हल
(ii) 3.5

प्रश्न 3.
संख्याओं -10, -6, -2, 2,….की सूची
(i) d = -16 वाली एक A.P. है
(ii) d = 4 वाली एक A.P. है
(iii) d = -4 वाली एक A.P. है
(iv) एक A.P. नहीं है
हल
(iii) d = 4 वाली एक A.P. है।

प्रश्न 4.
उस A.P., जिसका प्रथम पद -2 और सार्वान्तर -2 है के प्रथम चार पद हैं
(i) -2, 0, 2, 4
(ii) -2, 4, -8, 16
(iii) -2, -4, -6, -8
(iv) -2, -4, -8, -16
हल
(iii) -2, -4, -6, -8

प्रश्न 5.
उस A.P., जिसके प्रथम दो पद -3 और 4 हैं, का 21वाँ पद है
(i) 17
(ii) 137
(iii) 143
(iv) -143
हल
(ii) 137

प्रश्न 6.
यदि किसी A.P. का दूसरा पद 13 और 5वाँ पद 25 है, तो उसका 7वाँ पद क्या है?
(i) 30
(ii) 33
(iii) 37
(iv) 38
हल
(ii) 33

प्रश्न 7.
A.P.: 21, 42, 63, 84,… का कौन-सा पद 210 है?
(i) 9वाँ
(ii) 10वाँ
(iii) 11वाँ
(iv) 12वाँ
हल
(ii) 10वाँ

प्रश्न 8.
यदि किसी A.P. का सार्वान्तर 5 है, a₁₈ – a₁₃ क्या है?
(i) 5
(ii) 20
(iii) 25
(iv) 30
हल
(iii) 25

प्रश्न 9.
उस A.P. का सार्वान्तर क्या है, जिसमें a₁₈ – a₁₄ = 32 है?
(i) 8
(ii) -8
(iii) -4
(iv) 4
हल
(i) 8

प्रश्न 10.
दो समान्तर श्रेढ़ियों का एक ही सार्वान्तर है। इनमें से एक का प्रथम पद -1 और दसरी का प्रथम पद -8 है। तब, इनके चौथे पदों के बीच का अन्तर है
(i) -1
(ii) -8
(iii) 7
(iv) -9
हल
(iii) 7

प्रश्न 11.
यदि किसी A.P. के 7वें पद का 7 गुना उसके 11वें पद के 11 गुने के बराबर हो,तो उसका 18वाँ पद होगा
(i) 7
(ii) 11
(iii) 18
(iv) 0
हल
(iv) 0

प्रश्न 12.
A.P.: -11, -8, -5,…, 49 के अन्त से चौथा पद है
(i) 37
(ii) 40
(iii) 43
(iv) 58
हल
(ii) 40

प्रश्न 13.
यदि किसी A.P. का प्रथम पद -5 और सार्वान्तर 2 है तो उसके प्रथम 6 पदों का योग है
(i) 0
(ii) 5
(iii) 6
(iv) 15
हल
(i) 0

प्रश्न 14.
A.P.: 10, 6, 2,… के प्रथम 16 पदों का योग है
(i) -320
(ii) 320
(iii) -352
(iv) -400
हल
(i) -320

प्रश्न 15.
किसी A.P. में, यदि a = 1, a_n = 20 और S_n = 399 हों तो n बराबर है
(i) 19
(ii) 21
(iii) 38
(iv) 42
हल
(iii) 38

प्रश्न 16.
3 के प्रथम पाँच गुणजों का योग है
(i) 45
(ii) 55
(iii) 65
(iv) 75
हल
(i) 45

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
समान्तर श्रेढ़ी -4 + 3 + 10 +……..+ 52 में कितने पद हैं?
हल
माना समान्तर श्रेढ़ी -4 + 3 + 10 +………+ 52 में n पद हैं।
यहाँ, a = -4 तथा d = 3 – (-4) = 3 + 4 = 7
n वा पद = 52
⇒ a + (n – 1)d = 52
⇒ -4 + (n – 1)7 = 52
⇒ 7n – 7 = 52 + 4 = 56
⇒ 7n = 56 + 7 = 63
⇒ n = 9
अत: श्रेढ़ी में 9 पद हैं।

प्रश्न 2.
समान्तर श्रेढी 2, 7, 12, ……. का 20 वाँ पद निकालिए।
हल
दी हुई समान्तर श्रेढ़ी
2, 7, 12, ……
यहाँ, प्रथम पद (a) = 2, सार्वान्तर (d) = 7 – 2 = 5 तथा n = 20
n वाँ पद, a_n = a + (n – 1)d
20 वाँ पद, a₂₀ = 2 + (20 – 1) 5
= 2 + 19 × 5
= 2 + 95
= 97
अत : श्रेढ़ी का 20 वाँ पद = 97

प्रश्न 3.
प्रथम दस प्राकृतिक संख्याओं का योग ज्ञात कीजिए।
हल
प्रथम दस प्राकृतिक संख्याएँ :
1, 2, 3, 4, ………., 10
यहाँ, a = 1, d = 2 – 1 = 1, तथा n = 10
S₁₀ = n/2 [2a + (n – 1)d]
= 10/2 [2 × 1 + (10 – 1)1]
= 5[2 + 9]
= 55
अतः प्रथम दस प्राकृतिक संख्याओं का योग = 55

प्रश्न 4.
प्रथम 1000 धन पूर्णांकों का योग ज्ञात कीजिए।
हल
प्रथम 1000 धन पूर्णांकों की सूची है :
1, 2, 3,…..,1000
यह एक समान्तर श्रेढ़ी है जिसके लिए
a = 1, d = 2 – 1 = 1, n = 1000
सूत्र S_n = n/2 [2a + (n – 1) d] से
1000 पदों का योग, S₁₀₀₀ = 1000/2 [2(1) + (1000 – 1) (1)]
= 500 × 1001
= 500500
अत: प्रथम 1000 धन पूर्णांकों का योग = 500500

प्रश्न 5.
समान्तर श्रेढ़ी 21, 18, 15, …….. का आठवाँ पद ज्ञात कीजिए।
हल
दी हुई श्रेढ़ी 21, 18, 15,……..
यहाँ प्रथम पद (a) = 21, सार्वान्तर (d) = 18 – 21 = -3
श्रेढ़ी का n वाँ पद = a + (n – 1)d
श्रेढ़ी का 8 वाँ पद = 21 + (8 – 1) (-3) = 21 – 21 = 0
अत: श्रेढ़ी का आठवाँ पद शून्य है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
किसी समान्तर श्रेढी का दूसरा पद एवं पाँचवाँ पद क्रमशः 3 एवं -3 है, तो श्रेढी का सार्वान्तर एवं प्रथम पद ज्ञात कीजिए।
हल
माना श्रेढ़ी का प्रथम पद a तथा सार्वान्तर d है
श्रेढ़ी का दूसरा पद = a + d = 3 ……..(1)
पाँचवाँ पद = a + (5 – 1)d = -3
⇒ a + 4d = -3 …….(2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
(a + 4d) – (a + d) = -3 – 3
⇒ a + 4d – a – d = -6
⇒ 3d = -6
⇒ d = -2
d का मान समीकरण (1) में रखने पर,
a – 2 = 3
⇒ a = 3 + 2 = 5
अतः श्रेढ़ी का सार्वान्तर -2 तथा प्रथम पद 5 है।

प्रश्न 2.
किसी समान्तर श्रेढ़ी का n वाँ पद 2n + 5 है, तो श्रेढी के सात पदों तक योगफल ज्ञात कीजिए।
हल
दिया है, समान्तर श्रेढ़ी का n वाँ पद, (a_n) = 2n + 5
n = 1 रखने पर, प्रथम पद, (a₁) = 2 × 1 + 5 = 7
n = 2 रखने पर, दूसरा पद, (a₂) = 2 × 2 + 5 = 9
n = 3 रखने पर, तीसरा पद, (a₃) = 2 × 3 + 5 = 11
प्रथम पद (a) = 7, सार्वान्तर (d) = a₂ – a₁ = 9 – 7 = 2
सूत्र : S_n = n/2 [2a + (n – 1)d] से,
7 पदों तक योगफल, S₇ = 7/2 [2 × 7 + (7 – 1)2]
= 7/2 × 2[7 + 6]
= 7 × 13
= 91
अतः 7 पदों तक योगफल = 91

प्रश्न 3.
किसी समान्तर श्रेढ़ी का 7वाँ पद 32 और 13वाँ पद 62 है। समान्तर श्रेढी ज्ञात कीजिए।
हल
माना किसी समान्तर श्रेढ़ी का पहला पद a तथा सार्वान्तर d है।
दिया है, श्रेढ़ी का 7वाँ पद = 32
a + (7 – 1)d = 32
⇒ a + 6d = 32 ……(1)
इसी प्रकार, श्रेढ़ी का 13वाँ पद = 62
a + (13 – 1)d = 62
⇒ a + 12d = 62 ……..(2)
समीकरण (2) में से समीकरण (1) को घटाने पर,
6d = 62 – 32 = 30
d = 30/6 = 5
समीकरण (1) में d का मान रखने पर,
a + 6 × 5 = 32
⇒ a + 30 = 32
⇒ a = 32 – 30 = 2
तब, श्रेढ़ी : a, a + d, a + 2d, a + 3d,………
या 2, 2 + 5, 2 + 10, 2 + 15,………
या 2, 7, 12, 17, ………
अत: अभीष्ट समान्तर श्रेढ़ी : 2, 7, 12, 17, ……

प्रश्न 4.
समान्तर श्रेढ़ी 3, 5, 7, 9,…………, 201 का अन्तिम पद से (प्रथम पद की ओर) 15वाँ पद ज्ञात कीजिए।
हल
दी गई श्रेढ़ी 3, 5, 7, 9, …….., 201
प्रथम पद (a) = 3, दूसरा पद = 5, अन्तिम पद (l) = 201
सार्वान्तर (d) = दूसरा पद – पहला पद = 5 – 3 = 2
अन्त से nवाँ पद = l – (n – 1)d से,
n = 15 रखने पर,
अन्त से 15वाँ पद = l – (15 – 1)d (∵ l = 201)
= l – 14d
= 201 – (14 × 2)
= 201 – 28
= 173
अतः श्रेढ़ी का अन्त से 15वाँ पद = 173

प्रश्न 5.
किसी श्रेढी काn वाँ पद (2n + 1) है तो इस श्रेढी का सातवाँ (7th) पद ज्ञात कीजिए।
हल
माना समान्तर श्रेढ़ी का प्रथम पद a तथा सार्वान्तर d है।
दिया है, n वाँ पद an = 2n + 1
n = 1 रखने पर, प्रथम पद a = a₁ = 2 × 1 + 1 = 3
n = 2 रखने पर, दूसरा पद a₂ = 2 × 2 + 1 = 5
n = 3 रखने पर, तीसरा पद a₃ = 2 × 3 + 1 = 7
यहाँ पर a = 3, सार्वान्तर d = 5 – 3 = 2
सूत्र a_n = a + (n – 1)d से,
श्रेढ़ी का 7 वाँ पद a₇ = 3 + (7 – 1)2
= 3 + 6 × 2
= 15
अतः श्रेढी का 7 वाँ पद = 15

प्रश्न 6.
किसी समान्तर श्रेदी केn पदों का योग n(2n – 1) है, श्रेढ़ी का प्रथम पद, सार्वान्तर एवं श्रेढी ज्ञात कीजिए।
हल
दिया है, समान्तर श्रेढ़ी के n पदों तक योगफल,
S_n = n(2n – 1) = 2n² – n
n = 1 के लिए, प्रथम पद का योगफल S₁ = 2(1)² – 1 = 1
प्रथम पद (a) = 1
n = 2 के लिए, S₂ = 2(2)² – 2 = 8 – 2 = 6
दूसरा पद (a₂) = S₂ – S₁ = 6 – 1 = 5
n = 3 के लिए, S₃ = 2(3)² – 3 = 18 – 3 = 15
तीसरा पद (a₃) = S₃ – S₂ = 15 – 6 = 9
अतः श्रेढ़ी 1, 5, 9,…………
सार्वान्तर d = 5 – 1 = 4 तथा प्रथम पद a = 1.

प्रश्न 7.
0 से 50 के मध्य कितनी सम संख्याएँ हैं? उनका योगफल ज्ञात कीजिए।
हल
0 से 50 के मध्य सम संख्याएँ 2, 4, 6, 8,…, 48 तक माना n संख्याएँ हैं।
यहाँ a = 2 तथा d = 4 – 2 = 2
nवाँ पद = 48
⇒ 2 + (n – 1)2 = 48
⇒ 2 + 2n – 2 = 48
⇒ 2n = 48
⇒ n = 24
0 से 50 के मध्य 24 सम संख्याएँ होंगी।
24 संख्याओं का योगफल = 242 [2 × 2 + (24 – 1)2]
= 12 × 2(2 + 23)
= 24 × 25
= 600

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
एक आदमी पहले दिन ₹ 32, दूसरे दिन ₹ 36 तथा तीसरे दिन ₹ 40 बचाता है। यदि वह अपनी बचतों को इसी क्रम में जारी रखता है, तो कितने दिनों में उसकी कुल बचत ₹ 2000 होगी?
हल
पहले दिन बचत a₁ = ₹ 32
दूसरे दिन बचत a₂ = ₹ 36
तीसरे दिन बचत a₃ = ₹ 40
a₂ – a₁ = 36 – 32 = 4
a₃ – a₂ = 40 – 36 = 4
अन्तर नियत है
बचत समान्तर श्रेढ़ी में हैं।
प्रथम पद (a) = a₁ = 32 तथा सार्वान्तर (d) = 4
माना उसकी बचत n दिनों में ₹ 2000 होगी।
S_n = n/2 [2a + (n – 1)d]
⇒ 2000 = n/2 [2 × 32 + (n – 1)4]
⇒ 2000 = n/2 × 2[32 + (n – 1)2]
⇒ 2000 = n[32 + 2n – 2]
⇒ 2000 = 30n + 2n²
⇒ 2n² + 30n – 2000 = 0
⇒ n² + 15n – 1000 = 0
⇒ n² + (40 – 25)n – 1000 = 0
⇒ n² + 40n – 25n – 1000 = 0
⇒ n(n + 40) – 25(n + 40) = 0
⇒ (n + 40)(n – 25) = 0
यदि n + 40 = 0 तो n = -40 असम्भव
(क्योंकि दिनों की संख्या ऋणात्मक नहीं हो सकती)
यदि n – 25 = 0 तो n = 25
अत: आदमी की बचत 25 दिनों में ₹ 2000 होगी।

प्रश्न 2.
श्रेढ़ी 18, 15, 12, …….. का कौन-सा पद -87 है? क्या इस श्रेढ़ी का कोई पद शून्य है? यदि हाँ, तो कौन-सा पद?
हल
दी हुई श्रेढ़ी 18, 15, 12, ……
पहला पद (a) = 18 तथा सार्वान्तर (d) = 15 – 18 = -3
माना n वाँ पद -87 है।
n वाँ पद = -87
⇒ a + (n – 1)d = -87 [∵ n वाँ पद = a + (n – 1)d]
⇒ 18 + (n – 1)(-3) = -87
⇒ 18 – 3n + 3 = -87
⇒ -3n = -87 – 18 – 3 = -108
⇒ n = 108/3 = 36
अत: श्रेढ़ी का 36 वाँ पद -87 है।
पुनः माना श्रेढ़ी का nवाँ पद शून्य है।
nवाँ पद = 0
⇒ a + (n – 1)d = 0
⇒ 18 + (n – 1) (-3) = 0
⇒ -3(n – 1) = -18
⇒ n – 1 = 18/3 = 6
⇒ n = 6 + 1 = 7
अत: श्रेढ़ी का 7 वाँ पद शून्य है।

tense in english