bihar board class 10th maths | सांख्यिकी

Bihar Board Solutions for Class 10 Maths Chapter 14 Statistics (सांख्यिकी)

प्रश्नावली 14.1

प्रश्न 1. विद्यार्थियों के एक समूह द्वारा अपने पर्यावरण संचेतना अभियान के अन्तर्गत एक सर्वेक्षण किया गया, जिसमें उन्होंने एक मौहल्ले के 20 घरों में लगे हुए पौधों से सम्बन्धित निम्नलिखित आँकड़े एकत्रित किए। प्रति घर माध्य पौधों की संख्या ज्ञात कीजिए।

माध्य ज्ञात करने के लिए आपने किस विधि का प्रयोग किया और क्यों?
हल: हम आँकड़ों का माध्य प्रत्यक्ष (सरल)विधि से ज्ञात करेंगे क्योंकि अंक छोटे (कम) हैं।

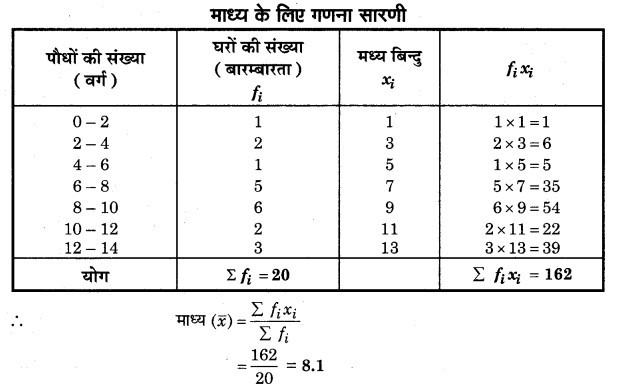
अतः प्रति घर में पौधों की औसत संख्या = 8.1 पौधे। यहाँ xi व fi के मान अत्यधिक कम होने के कारण प्रत्यक्ष विधि का प्रयोग किया गया है।

प्रश्न 2. किसी फैक्टरी के 50 श्रमिकों की दैनिक मजदूरी के निम्नलिखित बंटन पर विचार कीजिए:

एक उपयुक्त विधि का प्रयोग करते हुए, इस फैक्टरी के श्रमिकों की माध्य दैनिक मजदूरी ज्ञात कीजिए।
हल:

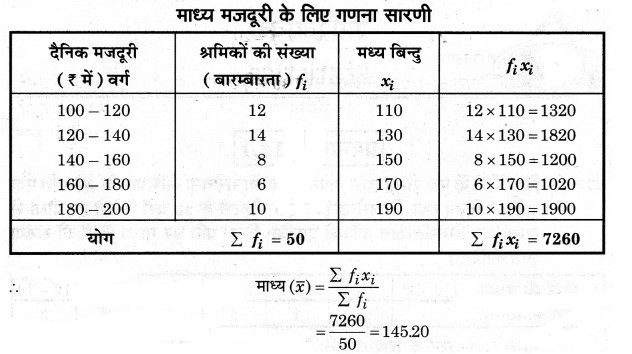
अतः श्रमिकों की माध्य दैनिक मजदूरी = ₹ 145.20

प्रश्न 3. निम्नलिखित बंटन एक मौहल्ले के बच्चों के दैनिक जेब खर्च दर्शाता है। माध्य जेब खर्च ₹ 18 है। लुप्त बारम्बारता f ज्ञात कीजिए:

हल: पहले दिए गए बंटन से औसत जेब खर्च निकाला जाएगा, तब गणना किए गए जेब खर्च और प्रश्न में दिए गए जेब खर्च में समानता स्थापित कर f का मान ज्ञात किया जा सकता है।

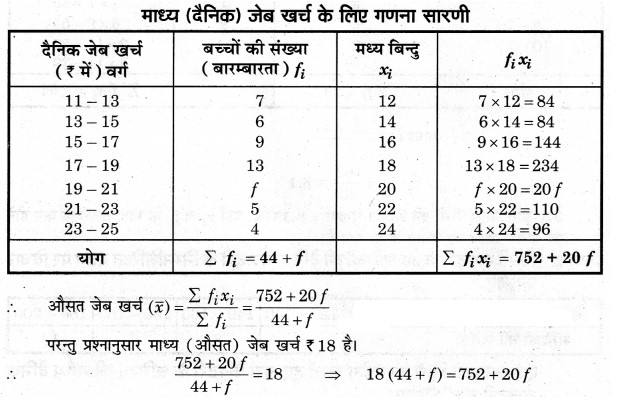
⇒ 792 + 18f = 752 + 20f
⇒ 2f = (792 – 752)
⇒ 2f = 40
⇒ f = 20
अतः लुप्त बारम्बारता f = 20

प्रश्न 4. किसी अस्पताल में, एक डॉक्टर द्वारा 30 महिलाओं की जाँच की गई और उनके हृदय स्पन्दन (beat) की प्रति मिनट संख्या नोट करके नीचे दर्शाए अनुसार संक्षिप्त रूप में लिखी गई। एक उपयुक्त विधि चुनते हुए, इन महिलाओं के हृदय स्पन्दन की प्रति मिनट माध्य संख्या ज्ञात कीजिए :

हल: यहाँ दिए गए वर्गों (65 – 68), (68 – 71),…….. के मध्य बिन्दु क्रमश: 66.5, 69.5, …… इत्यादि हैं; अतः विचलन विधि का प्रयोग उपयुक्त हैं।
प्रति मिनट हृदय स्पन्दन के माध्य हेतु गणना सारणी
माना स्पन्दन का कल्पित माध्य, A = 75.5 है।

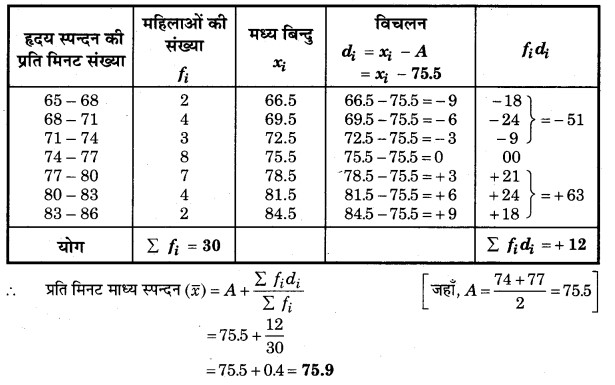
अत: महिलाओं के प्रति मिनट माध्य हृदय स्पन्दन की संख्या = 75.9

प्रश्न 5. किसी फुटकर बाजार में, फल विक्रेता पेटियों में रखे आम बेच रहे थे। इन पेटियों में आमों की संख्याएँ भिन्न-भिन्न थीं। पेटियों की संख्या के अनुसार, आमों का बंटन निम्नलिखित था:

एक पेटी में रखे आमों की माध्य संख्या ज्ञात कीजिए। आपने माध्य ज्ञात करने की किस विधि का प्रयोग किया है?
हल: माध्य के लिए गणना सारणी
माना प्रत्येक पेटी में आमों की कल्पित माध्य, A = 57 और वर्ग माप h = 3 है।

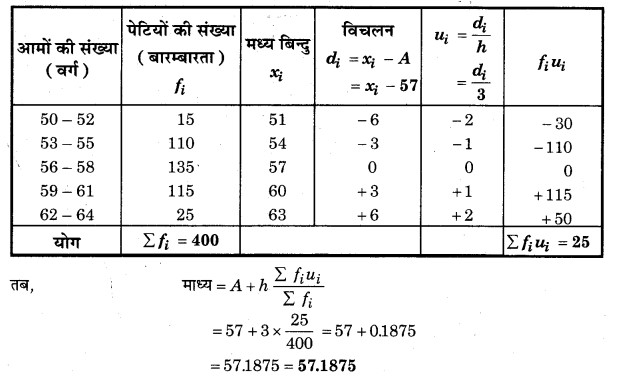
अत: आमों की माध्य संख्या = 57.1875 या 57.19
हमने माध्य ज्ञात करने के लिए कल्पित माध्य विधि का प्रयोग किया है।
वैकल्पिक विधि
चूँकि दिए गए आँकड़े सतत् नहीं है। अतः हम प्रत्येक वर्ग की उच्च सीमा में 0.5 जोड़ते हैं तथा निम्न सीमा में से 0.5 घटाते हैं।

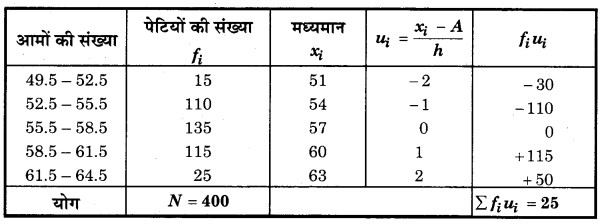
यहाँ, A = 57, h = 3, N = 400 तथा Σf_iu_i = 25
मानक विचलन विधि से,

अत: आमों की माध्य संख्या = 57.19

प्रश्न 6. निम्नलिखित सारणी किसी मौहल्ले के 25 परिवारों में भोजन पर हुए दैनिक व्यय को दर्शाती है :

एक उपयुक्त विधि द्वारा भोजन पर हुआ माध्य व्यय ज्ञात कीजिए।
हल: दैनिक भोजन व्यय की गणना हेतु सारणी
माना कल्पित माध्य, A = ₹ 225 और वर्ग माप, h = 50 है।

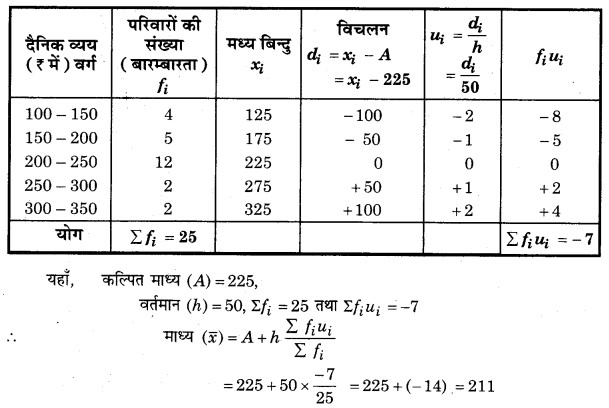
अतः प्रति परिवार भोजन पर होने वाले दैनिक व्यय का माध्य = ₹ 211

प्रश्न 7. वायु में सल्फर डाइ-ऑक्साइड (SO₂) की सान्द्रता (भाग प्रति मिलियन में) को ज्ञात करने के लिए, एक नगर के 30 मौहल्लों से आँकड़े एकत्रित किए गए, जिन्हें नीचे प्रस्तुत किया गया है :

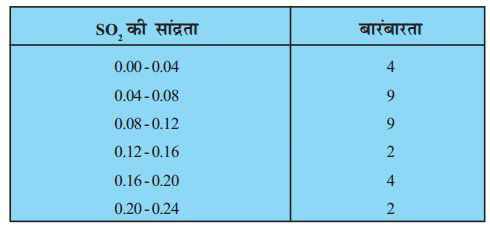
वायु में SO₂ की सान्द्रता का माध्य ज्ञात कीजिए।
हल: वायु में सल्फर डाइऑक्साइड (SO₂) की सान्द्रता ज्ञात करने के लिए गणना सारणी

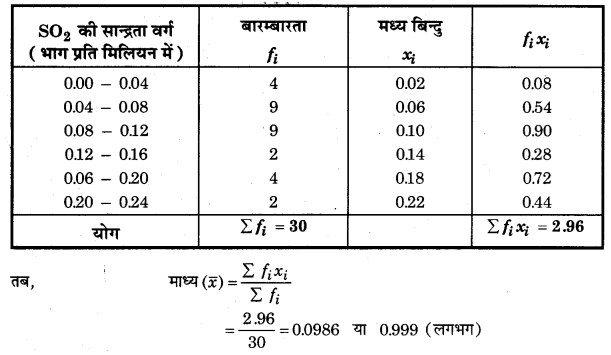
अत: वायु में SO₂ की सान्द्रता का माध्य = 0.999 भाग प्रति मिलियन।

प्रश्न 8. किसी कक्षा अध्यापिका ने पूरे सत्र के लिए अपनी कक्षा के 40 विद्यार्थियों की अनुपस्थिति निम्नलिखित रूप में रिकार्ड (record) की। एक विद्यार्थी जितने दिन अनुपस्थित रहा उनका माध्य ज्ञात कीजिए :

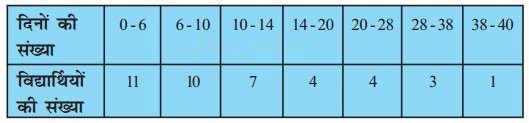
हल: विद्यार्थियों की माध्य अनुपस्थिति के लिए गणना सारणी

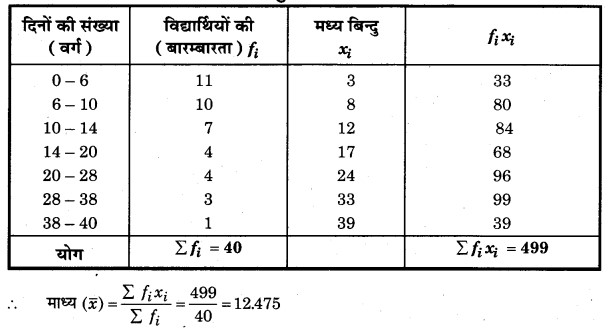
अतः विद्यार्थियों की अनुपस्थिति का माध्य = 12.75 ~ 12.48 दिन

प्रश्न 9. निम्नलिखित सारणी 35 नगरों की साक्षरता दर (प्रतिशत में) दर्शाती है। माध्य साक्षरता दर ज्ञात कीजिए:

हल: माध्य साक्षरता दर के लिए गणना सारणी
माना औसत साक्षरता दर का कल्पित माध्य, A = 70%

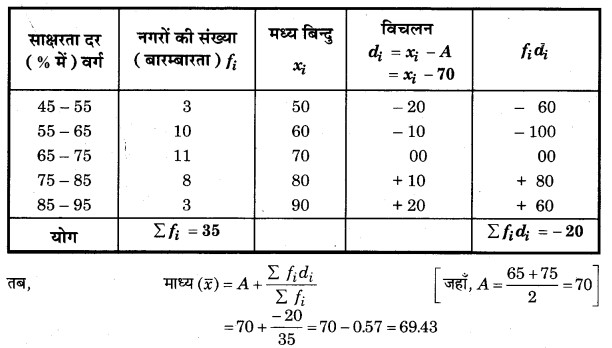
अत: साक्षरता दर के प्रतिशत का माध्य = 69.43

प्रश्नावली 14.2

प्रश्न 1.निम्नलिखित सारणी किसी अस्पताल में एक विशेष वर्ष में भर्ती हुए रोगियों की आयु को दर्शाती है:

उपर्युक्त आँकड़ों के बहुलक और माध्य ज्ञात कीजिए। दोनों केन्द्रीय प्रवृत्ति की मापों की तुलना कीजिए और उनकी व्याख्या कीजिए।
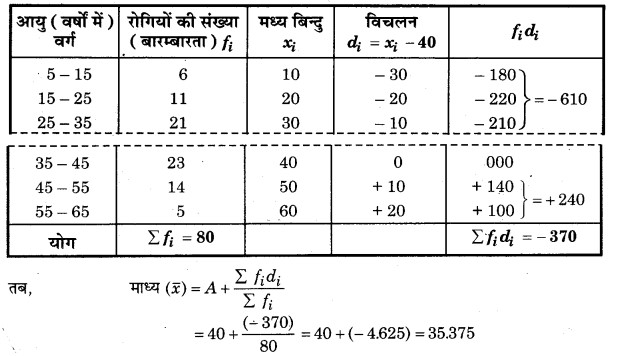
हल: केन्द्रीय प्रवृत्ति की मापों के लिए गणना सारणी
माना कल्पित माध्य A = 40

बहुलक के लिए : अधिकतम बारम्बारता वाला वर्ग = (35 – 45)
बहुलक वर्ग (Modal Class) = (35 – 45)
बहुलक वर्ग की निम्न सीमा (l₁) = 35
बहुलक वर्ग की उच्च सीमा (l₂) = 45
बहुलक वर्ग की बारम्बारता (f) = 23
बहुलक वर्ग के पूर्व वर्ग की बारम्बारता (f₁) = 21
बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता (f₂) = 14
बहुलक वर्ग का विस्तार (h) = l₂ – l₁ = 45 – 35 = 10

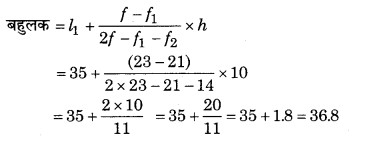
अत: आँकड़ों का माध्य = 35.375 वर्ष तथा बहुलक = 36.8 वर्ष।
इसका अर्थ है कि सम्बन्धित वर्ष में अधिकांश रोगी 36.8 वर्ष के हैं जबकि सभी रोगियों की औसत आयु 35.375 वर्ष है।

प्रश्न 2. निम्नलिखित आँकड़े 225 बिजली उपकरणों के प्रेक्षित जीवनकाल (घण्टों में) की सूचना देते हैं:

उपकरणों का बहुलक जीवनकाल ज्ञात कीजिए।
हल: दिए गए आँकड़ों का बहुलक वर्ग (60 – 80) है, क्योंकि इस वर्ग की बारम्बारता दिए गए आँकड़ों के वर्ग में सबसे अधिक है।
बहुलक वर्ग की निम्न सीमा (l₁) = 60
बहुलक वर्ग की उच्च सीमा (l₂) = 80
बहुलक वर्ग की बारम्बारता (f) = 61
बहुलक वर्ग के पूर्व वर्ग की बारम्बारता (f₁) = 52
बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता (f₂) = 38
बहुलक वर्ग का आकार या विस्तार (h) = l₂ – l₁ = 80 – 60 = 20

अत: उपकरणों का बहुलक जीवनकाल = 65.625 घण्टे।

प्रश्न 3. निम्नलिखित आँकड़े किसी गाँव के 200 परिवारों के कुल मासिक घरेलू व्यय के बंटन को दर्शाते हैं। इन परिवारों का बहुलक मासिक व्यय ज्ञात कीजिए। साथ ही, माध्य मासिक व्यय भी ज्ञात कीजिए।

हल: निरीक्षण से, बहुलक वर्ग = अधिकतम बारम्बारता वाला वर्ग = 1500 – 2000
बहुलक वर्ग की निम्न सीमा (l₁) = ₹ 1500
बहुलक वर्ग की उच्च सीमा (l₂) = ₹ 2000
बहुलक वर्ग का विस्तार (h) = l₂ – l₁ = 2000 – 1500 = ₹ 500
बहुलक वर्ग की बारम्बारता (f) = 40
बहुलक वर्ग के पूर्व वर्ग की बारम्बारता (f₁) = 24
बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता (f₂) = 33

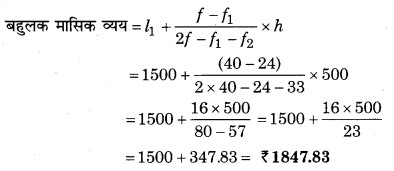
माध्य व्यय के लिए गणना सारणी
माना व्यय का कल्पित माध्य A = ₹ 2750 है और वर्ग विस्तार (माप) h = ₹ 500

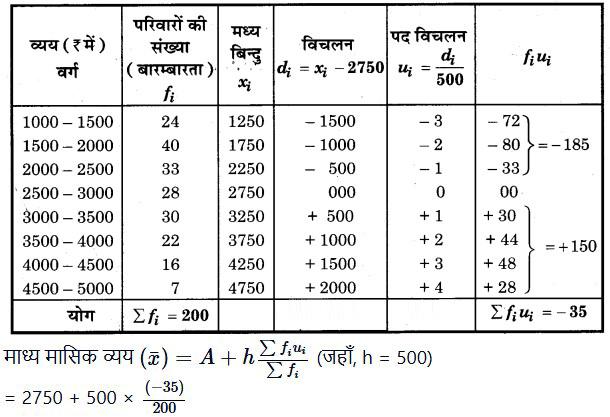
= 2750 + (2.5 × -35)
= 2750 + (-87.5)
= 2662.50
अतः व्यय का बहुलक = 1847.84 तथा व्यय का माध्य = ₹ 2662.50

प्रश्न 4. निम्नलिखित बंटन भारत के उच्चतर माध्यमिक स्कूलों में, राज्यों के अनुसार, शिक्षक-विद्यार्थी अनुपात को दर्शाता है। इन आँकड़ों के बहुलक और माध्य ज्ञात कीजिए। दोनों मापकों की व्याख्या कीजिए।

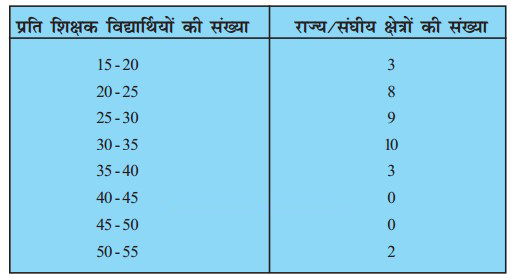
हल:
चूँकि सबसे अधिक बारम्बारता f = 10 है।
अत: इसका बहुलक वर्ग (30 – 35) है।
बहुलक वर्ग की निम्न सीमा (l₁) = 30
बहुलक वर्ग की उच्च सीमा (l₂) = 35
बहुलक वर्ग का विस्तार (h) = l₂ – l₁ = 35 – 30 = 5
बहुलक वर्ग की बारम्बारता (f) = 10
बहुलक वर्ग के पूर्व वर्ग की बारम्बारता (f₁) = 9
बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता (f₂) = 3


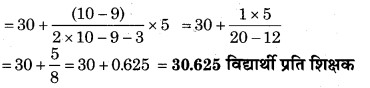
माध्य गणना हेतु सारणी
माना प्रति शिक्षक विद्यार्थियों की संख्या का कल्पित माध्य A = 27.5 है।

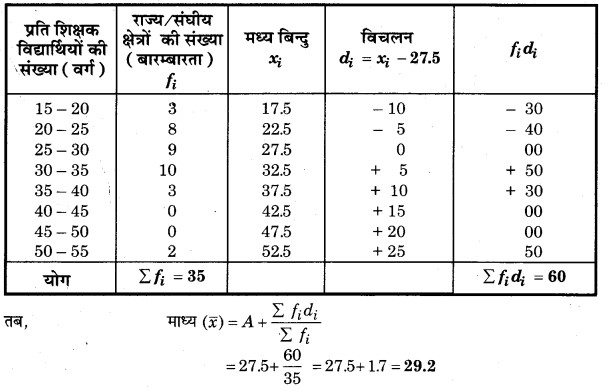
अत: भारत के उच्चतर माध्यमिक स्कूलों में राज्यों के अनुसार प्रति शिक्षक विद्यार्थियों का माध्य 29.2 है जबकि अधिकांश राज्यों में प्रति शिक्षक विद्यार्थियों की संख्या 30.625 है।

प्रश्न 5. दिया हुआ बंटन विश्व के कुछ श्रेष्ठतम बल्लेबाजों द्वारा एक दिवसीय अन्तर्राष्ट्रीय क्रिकेट मैचों में बनाए गए रनों को दर्शाता है :

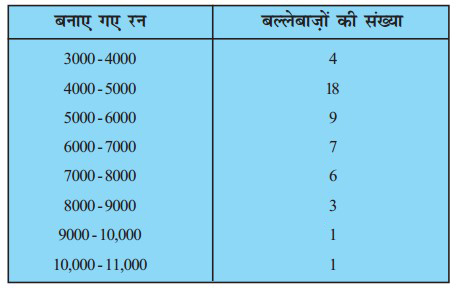
इन आँकड़ों का बहुलक ज्ञात कीजिए।
हल:
चूँकि अधिकतम बारम्बारता f = 18 है। इसलिए इसका बहुलक वर्ग (4000 – 5000) है।
बहुलक वर्ग की निम्न सीमा (l₁) = 4000
बहुलक वर्ग की उच्च सीमा (l₂) = 5000
बहुलक वर्ग का विस्तार (h) = 5000 – 4000 = 1000
बहुलक वर्ग की बारम्बारता (f) = 18
बहुलक वर्ग के पूर्व वर्ग की बारम्बारता (f₁) = 4
बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता (f₂) = 9

प्रश्न 6. एक विद्यार्थी ने एक सड़क के किसी स्थान से होकर जाती हुई कारों की संख्याएँ नोट की और उन्हें नीचे दी हुई सारणी के रूप में व्यक्त किया। सारणी में दिया प्रत्येक प्रेक्षण 3 मिनट के अन्तराल में उस स्थान से होकर जाने वाली कारों की संख्याओं से सम्बन्धित है। ऐसे 100 अन्तरालों पर प्रेक्षण लिए गए। इन आँकड़ों का बहुलक ज्ञात कीजिए।

हल:
चूँकि अधिकतम बारम्बारता 20 है। इसलिए इसका बहुलक वर्ग (40 – 50) है।
बहुलक वर्ग = 40 – 50
बहुलक वर्ग की निम्न सीमा (l₁) = 40
बहुलक वर्ग की उच्च सीमा (l₂) = 50
बहुलक वर्ग का विस्तार (h) = 50 – 40 = 10
बहुलक वर्ग की बारम्बारता (f) = 20
बहुलक वर्ग के पूर्व वर्ग की बारम्बारता (f₁) = 12
बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता (f₂) = 11

अत: सड़क पर प्रति तीन मिनट के अन्तरालों में अधिकांश अन्तरालों में गुजरने वाली कारों की संख्या (बहुलक) = 44.7

प्रश्नावली 14.3

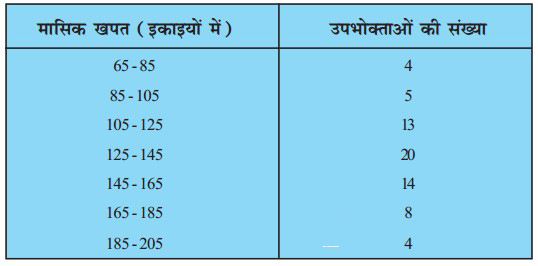
प्रश्न 1. निम्नलिखित बारम्बारता बंटन किसी मौहल्ले के 68 उपभोक्ताओं की बिजली की मासिक खपत दर्शाता है। इन आँकड़ों के माध्यिका, माध्य और बहुलक ज्ञात कीजिए। इनकी तुलना कीजिए।

हल: दिए गए बारम्बारता बंटन के लिए माध्य और माध्यिका की गणना सारणी
माना कल्पित माध्य, A = 115 तथा वर्ग माप, h = 20 है।

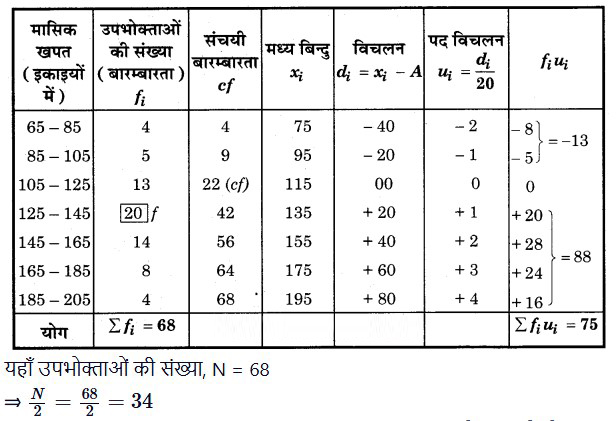
संचयी बारम्बारता सारणी से स्पष्ट है कि 34 संचयी बारम्बारता 42 के अन्तर्गत है, इसलिए (125 – 145) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l₁) = 125
माध्यिका वर्ग की उच्च सीमा (l₂) = 145
माध्यिका वर्ग का वर्ग विस्तार (h) = l₂ – l₁ = 245 – 125 = 20
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 22
माध्यिका वर्ग की बारम्बारता (f) = 20

बहुलक के लिए : चूँकि अधिकतम बारम्बारता f = 20 है। इसलिए इसका बहुलक वर्ग (125 – 145)
बहुलक वर्ग की निम्न सीमा (l₁) = 125
बहुलक वर्ग की उच्च सीमा (l₂) = 145
बहुलक वर्ग का विस्तार (h) = l₂ – l₁ = 145 – 125 = 20
बहुलक वर्ग की बारम्बारता (f) = 20
बहुलक वर्ग के ठीक पहले वर्ग की बारम्बारता (f₁) = 13
बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता (f₂) = 14

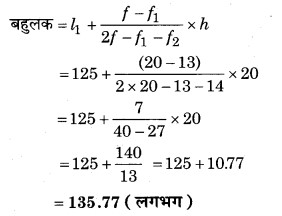
तुलनात्मक रूप से तीनों मापें लगभग समान हैं।

प्रश्न 2. यदि नीचे दिए गए बंटन का माध्यिका 28.5 हो, तो x और y के मान ज्ञात कीजिए :

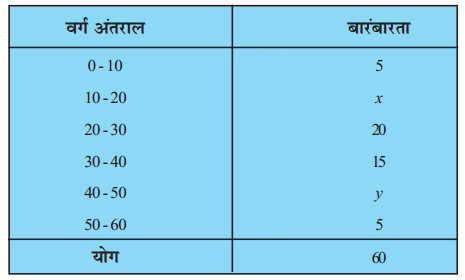
हल: संचयी बारम्बारता के लिए सारणी

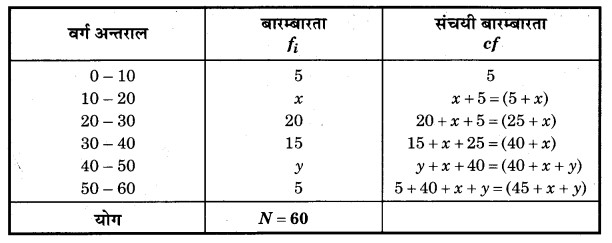
परन्तु बारम्बारताओं का योग N = 60 है।
अन्तिम वर्ग की संचयी बारम्बारता सभी बारम्बारताओं के योगफल के बराबर होती है।
45 + x + y = 60
⇒ x + y = 15 ……(1)
दिया है, माध्यिका 28.5 है।
माध्यिका वर्ग = (20 से 30 तक)
माध्यिका वर्ग की निम्न सीमा (l₁) = 20
माध्यिका वर्ग की अन्य सीमा (l₂) = 30
माध्यिका वर्ग का वर्ग विस्तार (h) = 30 – 20 = 10
माध्यिका वर्ग की बारम्बारता (f) = 20
माध्यिका वर्ग के पूर्व वर्ग की संचयी बारम्बारता (cf) = x + 5

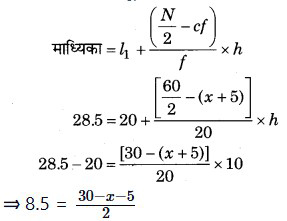
⇒ 17 = 25 – x
⇒ x = 25 – 17
⇒ x = 8 ……(2)
x का मान समी० (1) में रखने पर,
8 + y = 15
⇒ y = 15 – 8 = 7
अत: x = 8 तथा y = 7

प्रश्न 3. एक जीवन बीमा एजेण्ट 100 पॉलिसी धारकों की आयु के बंटन के निम्नलिखित आँकड़े ज्ञात करता है। माध्यिका आयु परिकलित कीजिए, यदि पॉलिसी केवल उन्हीं व्यक्तियों को दी जाती है, जिनकी आयु 18 वर्ष या उससे अधिक हो, परन्तु 60 वर्ष से कम हो।

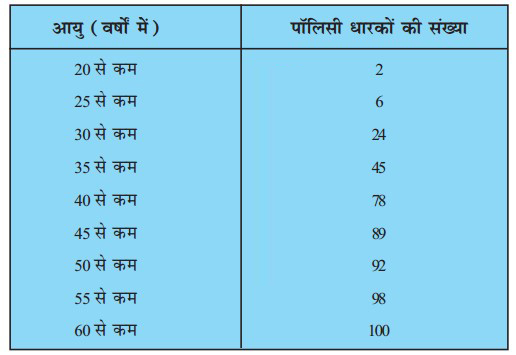
हल:

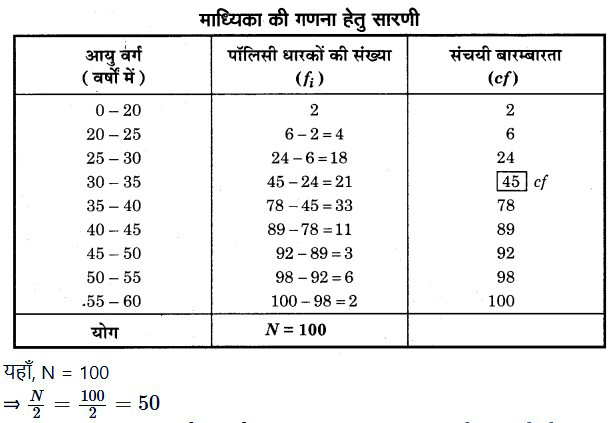
संचयी बारम्बारता सारणी से स्पष्ट है कि 50 संचयी बारम्बारता 78 के अन्तर्गत है, इसलिए (35 – 40) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l₁) = 35
माध्यिका वर्ग की उच्च सीमा (l₂) = 40
माध्यिका वर्ग (h) = l₂ – l₁ = 40 – 35 = 5
माध्यिका वर्ग की बारम्बारता (f) = 33
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 45

= 35 + 0.76
= 35.76 वर्ष (लगभग)
अत: माध्यिका = 35.76 वर्ष (लगभग)

प्रश्न 4. एक पौधे की 40 पत्तियों की लम्बाइयाँ निकटतम मिलीमीटरों में मापी जाती है तथा प्राप्त आँकड़ों को निम्नलिखित सारणी के रूप में निरूपित किया जाता है :

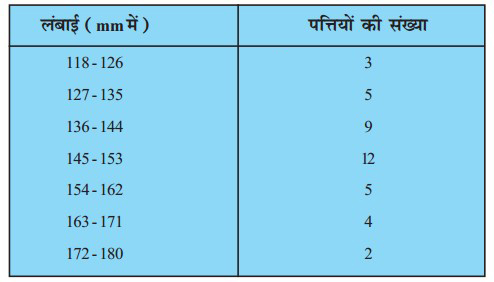
पत्तियों की माध्यिका लम्बाई ज्ञात कीजिए।
हल: चूँकि आँकड़ें सतत् नहीं है। अत: हमें माध्यिका ज्ञात करने के लिए इन्हें सतत् में बदलने की आवश्यकता है, तब वर्ग 117.5 – 126.5, 126.5 – 135.5…; 171.5 – 180.5 में बदल जाएँगे।
तब, परिकलित संचयी बारम्बारता सारणी

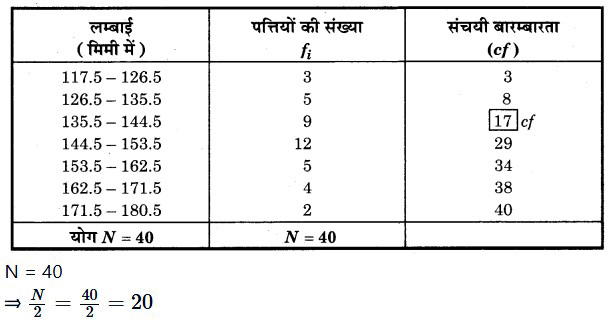
संचयी बारम्बारता सारणी से स्पष्ट है कि 20 संचयी बारम्बारता 29 के अन्तर्गत है, इसलिए (144.5 – 153.5) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l₁) = 144.5
माध्यिका वर्ग उच्च सीमा (l₂) = 153.5
वर्गमाप या माध्यिका वर्ग का वर्ग अन्तराल (h) = l₂ – l₁ = 153.5 – 144.5 = 9
.माध्यिका वर्ग की बारम्बारता (f) = 12
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 17

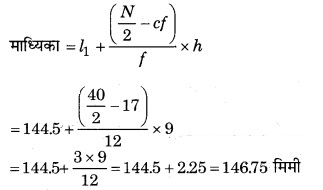
अत: पत्तियों की माध्यिका लम्बाई = 146.75 मिमी

प्रश्न 5. निम्नलिखित सारणी 400 निऑन लैम्पों के जीवनकालों (life time) को प्रदर्शित करती है:

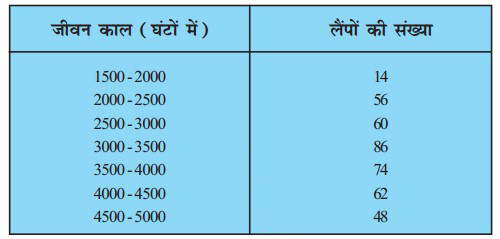
एक लैम्प का माध्यिका जीवनकाल ज्ञात कीजिए।
हल: माध्यिका हेतु संचयी बारम्बारता सारणी

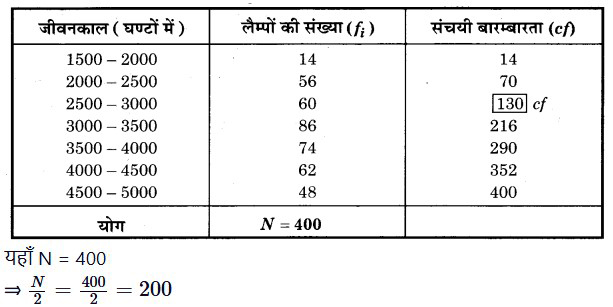
संचयी बारम्बारता सारणी से स्पष्ट है कि 200 संचयी बारम्बारता 216 के अन्तर्गत है, इसलिए (3000 – 3500) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l₁) = 3000
माध्यिका वर्ग की उच्च सीमा (l₂) = 3500
माध्यिका वर्ग का वर्ग अन्तराल (h) = l₂ – l₁ = 3500 – 3000 = 500
माध्यिका वर्ग की बारम्बारता (f) = 86
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 130

अत: लैम्पों का माध्यिका जीवनकाल = 3406.98 घण्टे

प्रश्न 6. एक स्थानीय टेलीफोन निर्देशिका से 100 कुलनाम (surnames) लिए गए और उनमें प्रयुक्त अंग्रेजी वर्णमाला के अक्षरों की संख्या का निम्नलिखित बारम्बारता बंटन प्राप्त हुआ:

कुलनामों में माध्यिका अक्षरों की संख्या ज्ञात कीजिए। कुलनामों में माध्य अक्षरों की संख्या ज्ञात कीजिए। साथ ही, कुलनामों का बहुलक ज्ञात कीजिए।
हल: माध्यिका एवं माध्य की गणना के लिए सारणी

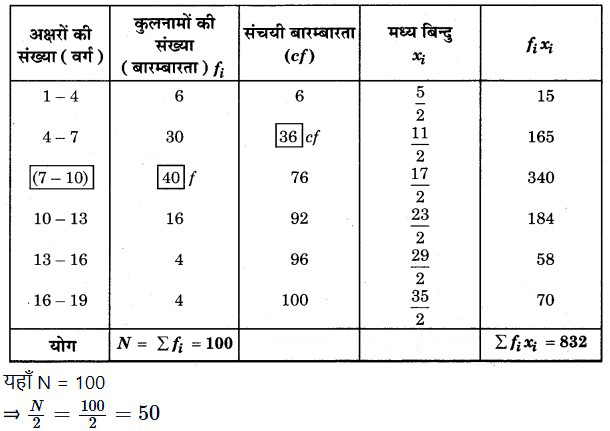
संचयी बारम्बारता सारणी से स्पष्ट है कि 50 संचयी बारम्बारता 76 के अन्तर्गत है, इसलिए (7 – 10) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l₁) = 7
माध्यिका वर्ग की उच्च सीमा (l₂) = 10
माध्यिका वर्ग का वर्ग अन्तराल (h) = l₂ – l₁ = 10 – 7 = 3
माध्यिका वर्ग की बारम्बारता (f) = 40
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 36

अतः कुलनामों में माध्य अक्षरों की संख्या 8.32 है।
बहुलक के लिए : बहुलक वर्ग = 7 – 10, है, क्योंकि इसकी अधिकतम बारम्बारता f = 40 है।
बहुलक वर्ग की निम्न सीमा (l₁) = 7
बहुलक वर्ग की उच्च सीमा (l₂) = 10
बहुलक वर्ग का वर्ग अन्तराल (h) = l₂ – l₁ = 10 – 7 = 3
बहुलक वर्ग की बारम्बारता (f) = 40
बहुलक वर्ग के ठीक पूर्व वर्ग की बारम्बारता (f₁) = 30
बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता (f₂) = 16

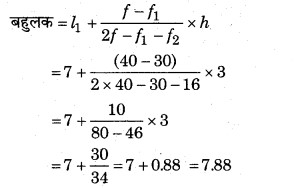
अतः कुलनामों का बहुलक 7.88 है।

प्रश्न 7. नीचे दिया हुआ बंटन एक कक्षा के 30 विद्यार्थियों के भार दर्शा रहा है। विद्यार्थियों का माध्यिका भार ज्ञात कीजिए।

हल: माध्यिका की गणना के लिए संचयी बारम्बारता सारणी

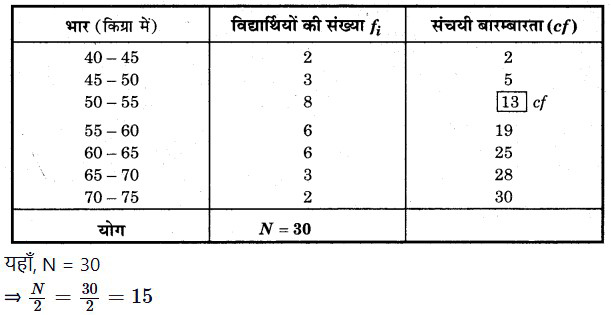
संचयी बारम्बारता सारणी से स्पष्ट है कि 15 संचयी बारम्बारता 19 के अन्तर्गत है, इसलिए (55 – 60) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l₁) = 55
माध्यिका वर्ग की उच्च सीमा (l₂) = 60
माध्यिका वर्ग का वर्ग अन्तराल (h) = l₂ – l₁ = 60 – 55 = 5
माध्यिका वर्ग की बारम्बारता (f) = 6
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 13

अत: विद्यार्थियों के भार का माध्यिका = 56.67 किग्रा (लगभग)

प्रश्नावली 14.4

प्रश्न 1. निम्नलिखित बंटन किसी फैक्टरी के 50 श्रमिकों की दैनिक आय दर्शाता है :

उपर्युक्त बंटन को एक कम प्रकार के संचयी बारम्बारता बंटन में बदलिए और उसका तोरण खींचिए।
हल: दिए गए बारम्बारता बंटन से “कम प्रकार” का संचयी बारम्बारता बंटन प्राप्त करना

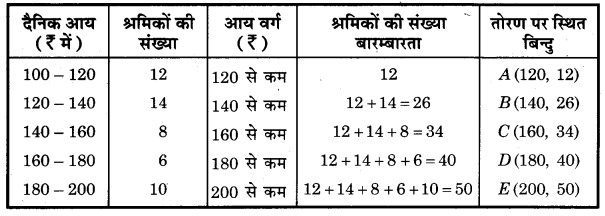
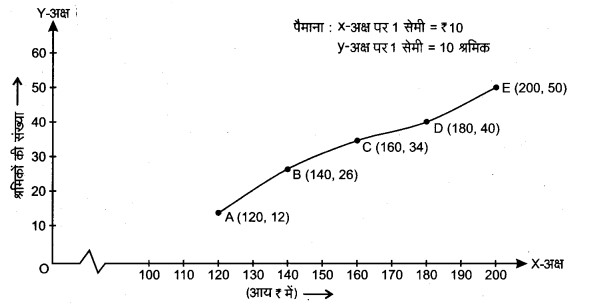
संचयी बारम्बारता वक्र (तोरण)

प्रश्न 2. किसी कक्षा के 35 विद्यार्थियों की मेडिकल जाँच के समय, उनके भार निम्नलिखित रूप में रिकार्ड किए गए :

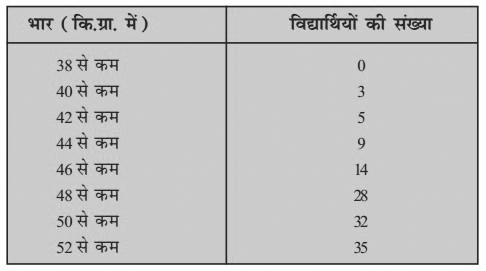
उपर्युक्त आँकड़ों के लिए कम प्रकार’ का तोरण खींचिए। इसके बाद माध्यिका भार ज्ञात कीजिए।
हल:

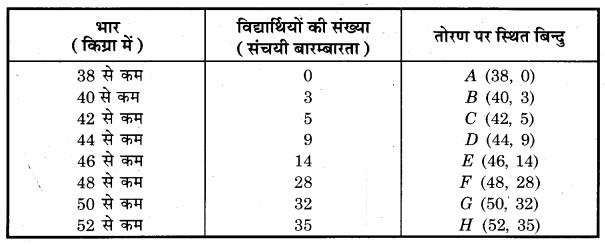
संचयी बारम्बारता वक्र (तोरण)

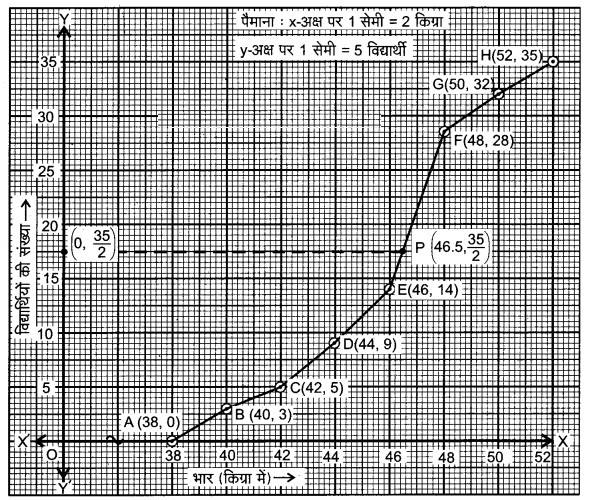
माध्यिका ज्ञात करना : बिंदु = 35/2 = 17.5, Y-अक्ष पर लेकर, X-अक्ष के समान्तर रेखा खींचते हैं। जोकि बिन्दु P पर मिलती है। बिन्दु P का भुज वक्र से ज्ञात करते हैं। यही प्रतिच्छेदी बिन्दु ही अभीष्ट माध्यिका है।
ग्राफ से, माध्यिका भार = 46.5 किग्रा, माध्यिका वर्ग (46 – 48) है।
दिया है, निम्न माध्यिका वर्ग (l₁) = 46, f = 14, cf = 14, वर्ग माप (h) = 2
कुल प्रेक्षण (N) = 35

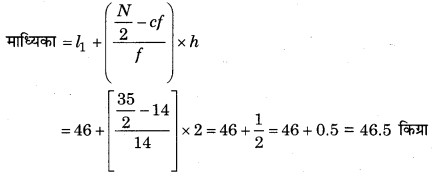
अत: माध्यिका समान है। जैसा कि हम ग्राफ से देखते हैं।

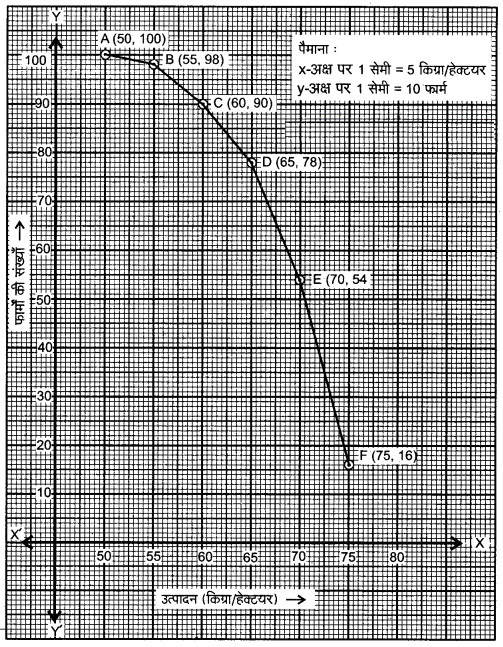
प्रश्न 3. निम्नलिखित सारणी किसी गाँव के 100 फार्मों में हुआ प्रति हेक्टेयर गेहूँ का उत्पादन दर्शाते हैं :

इस बंटन को से अधिक प्रकार के बंटन में बदलिए और फिर उसका तोरण खींचिए।
हल: दिए गए बंटन को ‘से अधिक’ प्रकार के बंटन में बदलना

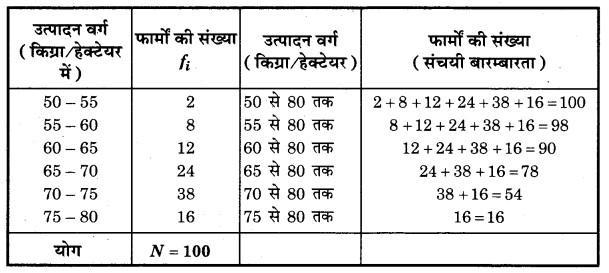
“से अधिक” प्रकार का बंटन

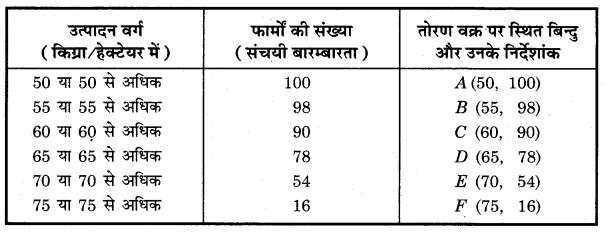
संचयी बारम्बारता वक्र (तोरण)

सांख्यिकी Additional Questions

बहुविकल्पीय प्रश्न

प्रश्न 1.
जब वर्गीकृत आँकड़ों के माध्य की गणना करते हैं, तो हम मानते हैं कि बारम्बारताएँ हैं
(i) सभी वर्गों के लिए समान बंटित
(ii) वर्गों के वर्ग अंक पर केन्द्रित
(iii) वर्गों की उच्च सीमा पर केन्द्रित
(iv) वर्गों की निम्न सीमा पर केन्द्रित
हल
(ii) वर्गों के वर्ग अंक पर केन्द्रित

प्रश्न 2.
वर्गीकृत आँकड़ों का ‘से कम प्रकार का’ और ‘से अधिक प्रकार का’ संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु के भुज (x-अक्ष) पर काटता है, तब इससे प्राप्त होता है
(i) माध्य
(ii) माध्यिका
(iii) बहुलक
(iv) ये सभी
हल
(ii) माध्यिका

प्रश्न 3.
निम्नलिखित बंटन के लिए

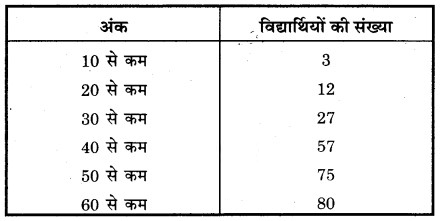
बहुलक वर्ग है
(i) 10 – 20
(ii) 20 – 30
(iii) 30 – 40
(iv) 50 – 60
हल
(iii) 30 – 40

प्रश्न 4.
निम्नलिखित बंटन में विद्यार्थियों की संख्या

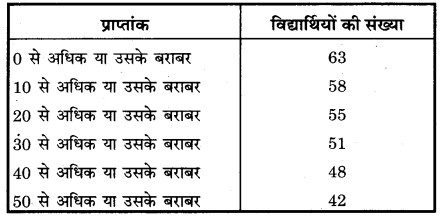
वर्ग 30 – 40 की बारम्बारता है
(i) 3
(ii) 4
(iii) 48
(iv) 51
हल
(i) 3

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
गणित विषय की परीक्षा में 10 छात्रों ने निम्नलिखित अंक प्राप्त किये
38, 17, 20, 8, 19, 35, 45, 15, 34, 14
प्राप्तांकों की माध्यिका ज्ञात कीजिए।
हल
पदों को आरोही क्रम में रखने पर,
8, 14, 15, 17, 19, 20, 34, 35, 38, 45
पदों की संख्या N = 10 है जो कि सम है।

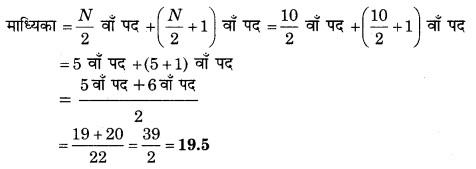
प्रश्न 2.
किसी बंटन का माध्य ज्ञात कीजिए यदि इसकी माध्यिका 45 और बहुलक 13 हो।
हल
बहुलक, माध्य तथा माध्यिका के बीच सम्बन्ध :
बहुलक = 3 × माध्यिका – 2 × माध्य
अथवा 2 × माध्य = 3 × माध्यिका – बहुलक
= 3 × 45 – 13
= 135 – 13
= 122
माध्य = 122/2 = 61

प्रश्न 3.
यदि किसी बंटन का माध्य 16 और बहुलक 13 हो तो बंटन माध्यिका ज्ञात कीजिए।
हल
बहुलक = 3 × माध्यिका – 2 × माध्य
⇒ 13 = 3(माध्यिका) – 2 × 16
⇒ 3(माध्यिका) = 13 + 32 = 45
⇒ माध्यिका = 45/3 = 15

प्रश्न 4.
यदि प्रेक्षणों x₁, x₂, x₃, ….., x_n, की बारम्बारताएँ क्रमशः f₁, f₂, f₃,…..,f_n हों तो इनका माध्य ज्ञात करने के लिए सूत्र लिखिए।
हल

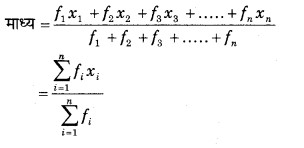
प्रश्न 5.
निम्न आँकड़ों का बहुलक ज्ञात कीजिए :
6, 9, 8, 7, 6, 7, 3, 6, 5, 6, 4
हल
उक्त आँकड़ों के निरीक्षण से हमें ज्ञात होता है कि आँकड़े 6 की आवृत्ति अधिकतम है।
अत: बहुलक = 6

प्रश्न 6.
बहुलक को परिभाषित कीजिए।
हल
आँकड़ों के किसी संग्रह या संकलन में जिस प्रेक्षण की आवृत्ति (बारम्बारता) अधिकतम होती है। उस प्रेक्षण को संग्रह का ‘बहुलक’ कहते हैं।

लघु उत्तरीय प्रश्न

प्रश्न 1.
निम्नलिखित आँकड़ों से माध्य ज्ञात कीजिए

हल

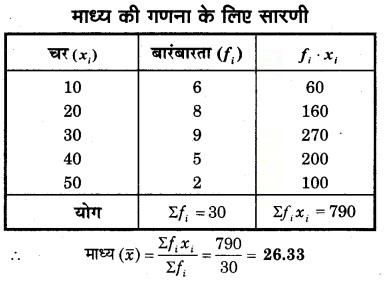
प्रश्न 2.
एक कक्षा के 50 छात्रों के भार नीचे की सारणी में प्रदर्शित हैं

इन छात्रों के भार का माध्य ज्ञात कीजिए।
हल
माना कल्पित माध्य, A = 47 किग्रा

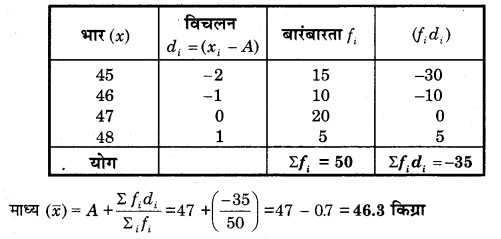
प्रश्न 3.
निम्नलिखित आँकड़ों का माध्य ज्ञात कीजिए

हल

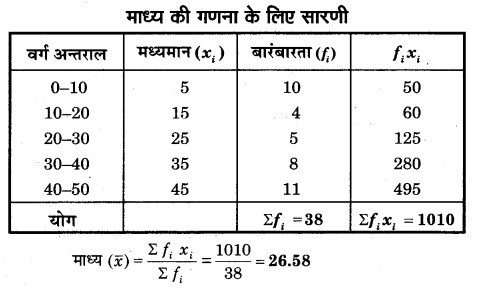
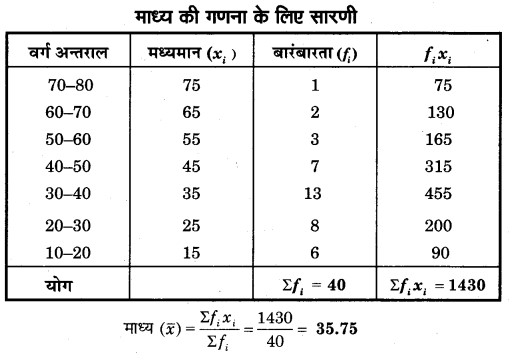
प्रश्न 4.
निम्नलिखित सारणी से माध्य की गणना कीजिए

हल

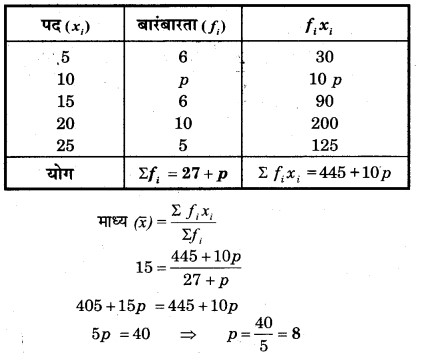
प्रश्न 5.
यदि निम्नांकित आँकड़ों का माध्य 15 है तो p का मान ज्ञात कीजिए

हल

प्रश्न 6.
यदि निम्नलिखित बारम्बारता बंटन का माध्य 1.46 है, तो f₁ और f₂ के मान ज्ञात कीजिए:

बारंबारताओं का कुल योगफल 200 है।
हल

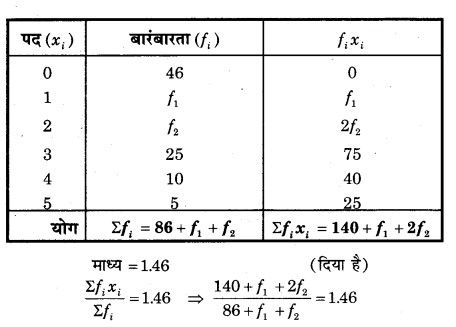
⇒ 140 + f₁ + 2f₂ = 1.46 (86 + f₁ + f₂) …….(1)
पुनः बारंबारताओं का योग 86 + f₁ + f₂ = 200
⇒ f₁ + f₂ = 114 …….(2)
समी० (2) से (f₁ + f₂) का मान समी० (1) में रखने पर,
140 + f₁ + 114 = 1.46(86 + 114)
⇒ f₁ = 292 – 254 = 38
समी० (2) से f₂ + 38 = 114
⇒ f₂ = 76
अत: f₁ और f₂ के मान क्रमशः 76 व 38 हैं।

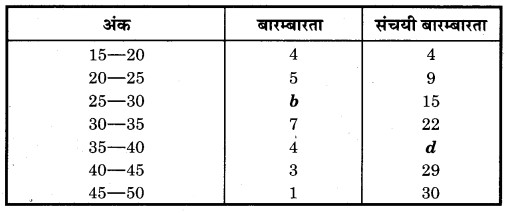
प्रश्न 7.
निम्नलिखित बारम्बारता बंटन सारणी को ध्यान से पढ़िए तथा b और d के मान लिखिए

हल
वर्ग 25 – 30 की संचयी बारम्बारता = 9 + b
प्रश्नानुसार, संचयी बारम्बारता = 15
⇒ 9 + b = 15
⇒ b = 15 – 9 = 6
इसी प्रकार, वर्ग 35 – 40 की संचयी बारम्बारता = 22 + 4 = 26
प्रश्नानुसार, संचयी बारम्बारता = d
⇒ d = 26
अतः b = 6 और d = 26

प्रश्न 8.
कक्षा X के 100 विद्यार्थियों द्वारा गणित में प्राप्त अंक नीचे सारणी में दिए गए हैं। प्राप्त अंकों का माध्यक ज्ञात कीजिए।

हल
असतत श्रेणी को सतत श्रेणी में बदलने पर,

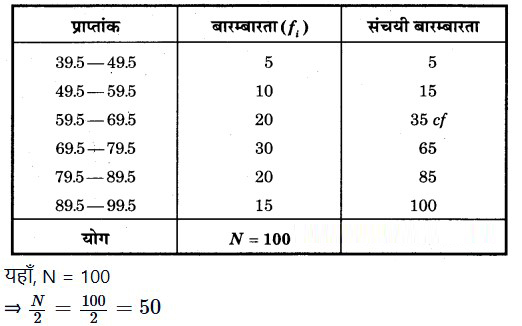
संचयी बारम्बारता से स्पष्ट है कि 50 संचयी बारम्बारता 65 के अन्तर्गत है, इसलिए (69.5 – 79.5) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l₁) = 69.5
माध्यिका वर्ग की उच्च सीमा (l₂) = 79.5
माध्यिका वर्ग का वर्ग अन्तराल (h) = l₂ – l₁ = 79.5 – 69.5 = 10
माध्यिका वर्ग की बारम्बारता (f) = 30
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 35

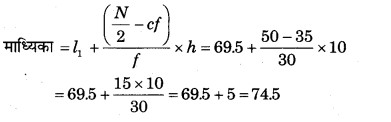
दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
निम्नलिखित बारंबारता बंटन का माध्य लघु विधि (विचलन विधि) से ज्ञात कीजिए

हल
माना कल्पित माध्य, A = 35 है।

प्रश्न 2.
निम्नलिखित बंटनों की माध्यिका ज्ञात कीजिए

हल
उपर्युक्त बंटन की संचयी बारंबारता सारणी निम्नवत् है

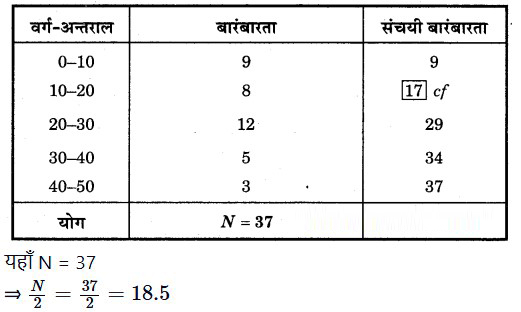
संचयी बारम्बारता सारणी से स्पष्ट है कि 18.5 संचयी बारम्बारता 29 के अन्तर्गत है, इसलिए (20 – 30) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l₁) = 20
माध्यिका वर्ग की उच्च सीमा (l₂) = 30
माध्यिका वर्ग का वर्ग अन्तराल (h) = l₂ – l₁ = 30 – 20 = 10
माध्यिका वर्ग की बारम्बारता (f) = 12
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 17

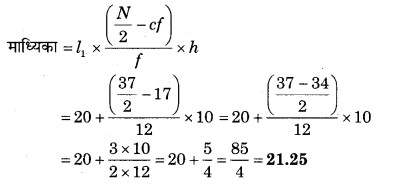
प्रश्न 4.
निम्नलिखित बारम्बारता बंटन के लिए माध्य ज्ञात कीजिए :

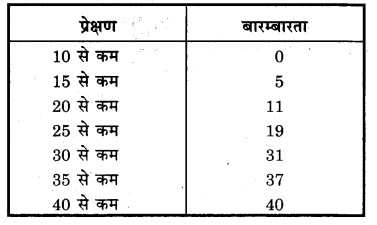
हल

tense in english