bihar board class 10th maths | Areas Related to Circles (वृतों से सम्बंधित क्षेत्रफल)

20 March 20217 May 2025

Bihar Board Solutions for Class 10 Maths Chapter 12 Areas Related to Circles (वृतों से सम्बंधित क्षेत्रफल)

प्रश्नावली 12.1

प्रश्न 1. दो वृत्तों की त्रिज्याएँ क्रमशः 19 cm और 9 cm हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है।
हल:
पहले वृत्त की त्रिज्या (r₁) = 19 cm
पहले वृत्त की परिधि = 2πr₁ = 2π × 19 = 38π cm
इसी प्रकार, दूसरे वृत्त की त्रिज्या (r₂) = 9 cm
दूसरे वृत्त की परिधि = 2πr₂ = 2π × 9 = 18π cm
दोनों वृत्तों की परिधियों का योग = (38π + 18π) = 56π cm
वांछित वृत्त की परिधि = 56π cm
माना वांछित वृत्त की त्रिज्या = r cm
तब, वांछित वृत्त की परिधि = 56π m
⇒ 2πr = 56π

अतः अभीष्ट वृत्त की त्रिज्या = 28 cm

प्रश्न 2. दो वृत्तों की त्रिज्याएँ क्रमशः 8 cm और 6 cm हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसका क्षेत्रफल इन दोनों वृत्तों के क्षेत्रफलों के योग के बराबर है।
हल:
पहले वृत्त की त्रिज्या (r₁) = 8 cm
पहले वृत्त का क्षेत्रफल = πr²₁ = π × 8 × 8 = 64π cm²
इसी प्रकार, दूसरे वृत्त की त्रिज्या (r₂) = 6 cm
दूसरे वृत्त का क्षेत्रफल = πr²₂ = π × 6 × 6 = 36π cm²
दोनों वृत्तों के क्षेत्रफलों का योग = 64π + 36π = 100π cm²
वांछित वृत्त का क्षेत्रफल = 100π cm²
माना वांछित वृत्त की त्रिज्या r cm है।
तब, वांछित वृत्त का क्षेत्रफल = 100π cm²
⇒ πr² = 100π
⇒ r² = 100π
⇒ r = √100 = 10
अतः अभीष्ट वृत्त की त्रिज्या = 10 cm

प्रश्न 3. दी गई आकृति एक तीरंदाजी लक्ष्य को दर्शाती है, जिसमें केन्द्र से बाहर की ओर पाँच क्षेत्र GOLD, RED, BLUE, BLACK और WHITE चिह्नित हैं, जिनसे अंक अर्जित किए जा सकते हैं। GOLD अंक वाले क्षेत्र GOLD का व्यास 21 cm है तथा प्रत्येक अन्य पट्टी 10.5 cm चौड़ी है। अंक प्राप्त कराने वाले इन पाँचों क्षेत्रों में से प्रत्येक का क्षेत्रफल ज्ञात कीजिए।

हल:
सबसे पहले क्षेत्र का व्यास = 21 cm
GOLD क्षेत्र की त्रिज्या R_G = 21/2 = 10.5 cm
और अगली प्रत्येक पट्टी की चौड़ाई = 10.5 cm
तीरंदाजी के पाँच क्षेत्रों का क्रम = GOLD, RED, BLUE, BLACK, WHITE
RED क्षेत्र की भीतरी त्रिज्या R_r2 = 10.5 cm
तथा बाहरी त्रिज्या R_r1 = R_r2 + 10.5 cm = 10.5 + 10.5 = 21.0 cm
तब, BLUE क्षेत्र की भीतरी त्रिज्या R_B2 = 21.0 cm
तथा बाहरी त्रिज्या R_B1 = R_B2 + 10.5 cm = 21.0 + 10.5 = 31.5 cm
तब, BLACK क्षेत्र की भीतरी त्रिज्या R_b2 = 31.5 cm
तथा बाहरी त्रिज्या R_b1 = R_b2 + 10.5 cm = 31.5 + 10.5 = 42.0 cm
तब, WHITE क्षेत्र की भीतरी त्रिज्या R_w2 = 42.0 cm
बाहरी त्रिज्या R_w1 = R_w2 + 10.5 cm = 42.0 + 10.5 = 52.5 cm
इस प्रकार क्षेत्रवार त्रिज्याएँ :

प्रश्न 4. किसी कार के प्रत्येक पहिए का व्यास 80 cm है। यदि यह कार 66 km प्रति घण्टे की चाल से चल रही है तो 10 मिनट में प्रत्येक पहिया कितने चक्कर लगाता है?
हल:
कार के पहिए का व्यास = 80 cm
कार के पहिए की परिधि = π × व्यास

= 110000 cm/min
∴ कार द्वारा 10 मिनट में चली दूरी = चाल × समय
= 110000 × 10
= 1100000 cm
∴ 10 मिनट में चली दूरी 1100000 cm के लिए पहिए के चक्करों की संख्या

अत: 10 मिनट में कार का प्रत्येक पहिया 4375 चक्कर लगाएगा।

प्रश्न 5. निम्नलिखित में सही उत्तर चुनिए तथा अपने उत्तर का औचित्य दीजिए-
यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप से बराबर है तो उस वृत्त की त्रिज्या है-
(A) 2 मात्रक
(B) π मात्रक
(C) 4 मात्रक
(D) 7 मात्रक
हल:
माना वृत्त की त्रिज्या = R
तब, वृत्त का परिमाप (परिधि) = 2πR
और वृत्त का क्षेत्रफल = πR²
संख्यात्मक रूप से, वृत्त का क्षेत्रफल = वृत्त का परिमाप
πR² = 2πR
R = 2 (दोनों पक्षों को πR से भाग देने पर)
वृत्त की त्रिज्या = 2 मात्रक
अत: विकल्प (A) सही है।

प्रश्नावली 12.2

प्रश्न 1. 6 cm त्रिज्या वाले एक वृत्त के एक त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60° है।
हल:
वृत्त की त्रिज्या (r) = 6 cm
त्रिज्यखण्ड का कोण (θ) = 60°
तब, त्रिज्यखण्ड का क्षेत्रफल

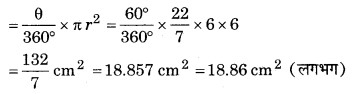
अत: त्रिज्यखण्ड का क्षेत्रफल = 18.86 cm² (लगभग) या 132/7 cm²

प्रश्न 2. एक वृत्त के चतुर्थांश (quadrant) का क्षेत्रफल ज्ञात कीजिए जिसकी परिधि 22 cm है।
हल: दिया है, वृत्त की परिधि (2πr) = 22 cm

अत: अभीष्ट क्षेत्रफल = 9.625 cm²

प्रश्न 3. एक घड़ी की मिनट की सुई की लम्बाई 14 cm है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए।
हल: मिनट की सुई 1 घण्टे या 60 मिनट में 1 पूरा चक्कर लगाती है

प्रश्न 4. 10 cm त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर एक समकोण अन्तरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए-
(i) संगत लघु वृत्तखण्ड
(ii) संगत त्रिज्यखण्ड (π = 3.14 का प्रयोग कीजिए)।
हल:
(i) वृत्त की त्रिज्या (r) = 10 cm
जीवा द्वारा केन्द्र पर अन्तरित कोण (θ) = 90°
संगत लघ वत्तखण्ड का क्षेत्रफल
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2 Q4
अतः संगत लघु वृत्तखण्ड का क्षेत्रफल = 28.5 cm²

(ii) संगत त्रिज्यखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड का क्षेत्रफल
= πr² – 28.5
= 3.14 × (10)² – 28.5
= 314 – 28.5
= 285.5
अत: संगत त्रिज्यखण्ड का क्षेत्रफल = 285.5 cm²

प्रश्न 5. त्रिज्या 21 cm वाले वृत्त का एक चाप केन्द्र पर 60° का कोण अन्तरित करता है। ज्ञात कीजिए-
(i) चाप की लम्बाई,
(ii) चाप द्वारा बनाए गए त्रिज्यखण्ड का क्षेत्रफल,
(iii) संगत जीवा द्वारा बनाए गए वृत्तखण्ड का क्षेत्रफल।
हल:
दिया है, वृत्त की त्रिज्या (r) = 21 cm
तथा चाप द्वारा केन्द्र पर बना कोण (θ) = 60°
(i) चाप की लम्बाई (l)
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2 Q5
अतः चाप की लम्बाई (l) = 22 cm

(ii) चाप द्वारा बनाए गए त्रिज्यखण्ड का क्षेत्रफल

अत: अभीष्ट त्रिज्यखण्ड का क्षेत्रफल = 231 cm²

(iii) संगत जीवा द्वारा बने वृत्तखण्ड का क्षेत्रफल
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2 Q5.2
अत: अभीष्ट वृत्तखण्ड का क्षेत्रफल = 40.05 cm²

प्रश्न 6. 15 cm त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर 60° का कोण अन्तरित करती है। संगत लघु और दीर्घ वृत्तखण्डों के क्षेत्रफल ज्ञात कीजिए। (π = 3.14 और √3 = 1.73) का प्रयोग कीजिए।
हल:
वृत्त की त्रिज्या (r) = 15 cm
जीवा द्वारा केन्द्र पर अन्तरित कोण (θ) = 60°
संगत लघु वृत्तखण्ड का क्षेत्रफल
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2 Q6

तब, संगत दीर्घ वृत्तखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड का क्षेत्रफल
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2 Q6.2
अतः लघु वृत्तखण्ड का क्षेत्रफल = 20.4375 cm²
तथा दीर्घ वृत्तखण्ड का क्षेत्रफल = 686.0625 cm²

प्रश्न 7. त्रिज्या 12 cm वाले एक वृत्त की कोई जीवा केन्द्र पर 120° का कोण अन्तरित करती है। संगत वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए।
(π = 3.14 और √3 = 1.73 का प्रयोग कीजिए।)
हल:
वृत्त की त्रिज्या (r) = 12 सेमी
तथा जीवा द्वारा केन्द्र पर अन्तरित कोण (θ) = 120°
संगत (लघु) वृत्तखण्ड का क्षेत्रफल

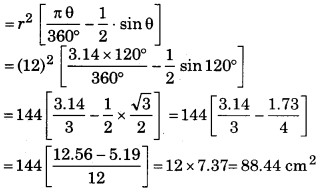
अतः अभीष्ट वृत्तखण्ड का क्षेत्रफल = 88.44 cm²

प्रश्न 8. 15 cm भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूटे से एक घोड़े को 5 m लम्बी रस्सी से बाँध दिया गया है। ज्ञात कीजिए-
(i) मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
(ii) चरे जा सकने वाले क्षेत्रफल में वृद्धि यदि घोड़े को 5 m लम्बी रस्सी के स्थान पर 10 m लम्बी रस्सी से बाँध दिया जाए। (π = 3.14 का प्रयोग कीजिए।)

हल:
वर्गाकार मैदान की भुजा = 15 m
पूरे मैदान का क्षेत्रफल = (भुजा)² = (15)² = 225 m²
(i) घोड़ा एक 5 मीटर लम्बी रस्सी से बँधा है, तब वह अधिकतम 5 मीटर त्रिज्या वाले वृत्त के उस त्रिज्यखण्ड की घास चर सकेगा जिसका कोण वर्ग के अन्त:कोण के बराबर अर्थात् 90° है।
तब, त्रिज्यखण्ड का क्षेत्रफल
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.2 Q8.1
अत: घोड़ा 19.625 m² क्षेत्रफल की घास चर सकता है।

(ii) यदि रस्सी की लम्बाई 10 मीटर कर दी जाए अर्थात् त्रिज्या r = 10 मीटर हो तो त्रिज्यखण्ड का क्षेत्रफल

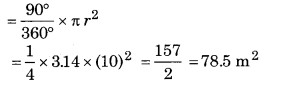
अब घोड़ा 78.5 m² क्षेत्र की घास चर सकेगा।
अतः क्षेत्रफल में वृद्धि = 78.5 – 19.625 = 58.875 m²

प्रश्न 9. एक वृत्ताकार ब्रच (brooch) को चाँदी के तार से बनाया जाना है जिसका व्यास 35 mm है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखण्डों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है तो ज्ञात कीजिए-
(i) कुल वांछित चाँदी के तार की लम्बाई।
(ii) ब्रूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल।

हल:
दिया है, वृत्ताकार ब्रूच का व्यास = 35 mm
⇒ त्रिज्या (r) = 35/2 mm
(i) चाँदी के ब्रूच के वृत्तीय भाग की माप = π × व्यास
= 22/7 × 35
= 110 mm
और 5 व्यासों की लम्बाई = 5 × 35 = 175 mm
अतः चाँदी के तार की कुल लम्बाई = 110 + 175 = 285 mm = 28.5 cm

अत: ब्रूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल = 96.25 mm²

प्रश्न 10. एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगी हुई हैं। छतरी को 45 cm त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।

हल:
दिया है, छतरी की त्रिज्या (r) = 45 cm
दो क्रमागत तारों के मध्य एक त्रिज्यखण्ड बनेगा।

प्रश्न 11. किसी कार के दो वाइपर (wipers) हैं, परस्पर कभी आच्छादित नहीं होते हैं। प्रत्येक वाइपर की पत्ती की लम्बाई 25 cm है और 115° के कोण तक घूमकर सफाई कर सकता है। पत्तियों की प्रत्येक बहार के साथ जितना क्षेत्रफल साफ हो जाता है, वह ज्ञात कीजिए।
हल: प्रत्येक वाइपर की सफाई का क्षेत्र उस त्रिज्यखण्ड का क्षेत्रफल होगा जिसकी त्रिज्या (r) = पत्ती की लम्बाई = 25 cm
तथा त्रिज्यखण्ड का कोण (θ) = 115°
तब, प्रत्येक वाइपर के द्वारा साफ हुआ क्षेत्रफल = त्रिज्यखण्ड का क्षेत्रफल

प्रश्न 12. जहाजों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए एक लाइट हाउस (light house) 80° कोण वाले एक त्रिज्यखण्ड में 16.5 km की दूरी तक लाल रंग का प्रकाश फैलाता है। समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए। जिसमें जहाजों को चेतावनी दी जा सके।(π = 3.14 का प्रयोग कीजिए।)
हल:
दिया है, त्रिज्यखण्ड का कोण (θ) = 80°

अतः समुद्र के उस भाग, जहाँ जहाजों को चेतावनी दी जा सके, का क्षेत्रफल = 189.97 km²

प्रश्न 13. एक गोल मेजपोश पर छह समान डिजाइन बने हुए हैं जैसा कि आकृति में दर्शाया गया है। यदि मेजपोश की त्रिज्या 28 cm है तो ₹ 0.35 प्रति वर्ग सेंटीमीटर की दर से इन डिजाइनों को बनाने की लागत ज्ञात कीजिए। (√3 = 1.7 का प्रयोग त्रिी कीजिए)

हल:
दिया है, मेजपोश के वृत्त की त्रिज्या (r) = 28 cm
सभी डिजाइनों के क्षेत्रफल समान हैं,
प्रत्येक वृत्तखण्ड का क्षेत्रफल और जीवाओं द्वारा केन्द्र पर अन्तरित कोण θ समान हैं तथा प्रत्येक 60° है।

₹ 0.35 प्रति वर्ग सेमी की दर से डिजाइन कराने का व्यय = ₹ (0.35 × 464.8) = ₹ 162.68
अत: डिजाइनों को बनाने की लागत = ₹ 162.68

प्रश्न 14. निम्नलिखित में सही उत्तर चुनिए-
त्रिज्या R वाले वृत के उस त्रिज्यखण्ड का क्षेत्रफल जिसका कोण p° है, निम्नलिखित है-

हल:
दिया है, वृत्त की त्रिज्या = R
तथा त्रिज्यखण्ड का कोण (θ) = p°
त्रिज्यखण्ड का क्षेत्रफल

अत: विकल्प (D) सही है।

प्रश्नावली 12.3

(जब तक अन्यथा न कहा जाए, π = $\frac { 22 }{ 7 }$ का प्रयोग कीजिए।)

प्रश्न 1. दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 cm, PR = 7 cm तथा O वृत्त का केन्द्र है।

हल:
दिया है, PQ = 24 cm, PR = 7 cm
O वृत्त का केन्द्र है।
QR व्यास है।
तब, वृत्त की त्रिज्या (r) = QR/2
∆PQR समकोणीय होगा क्योंकि अर्द्धवृत्त में बना कोण समकोण होता है।
तब, समकोण ∆PQR में, [∵ ∠QPR = 90°]
पाइथागोरस प्रमेय से,
QR² = PQ² + PR²
= (24)² + (7)²
= 576 + 49
= 625

प्रश्न 2. दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केन्द्र O वाले दोनों संकेन्द्रीय वृत्तों की त्रिज्याएँ क्रमशः 7 cm और 14 cm हैं तथा ∠AOC = 40° है।

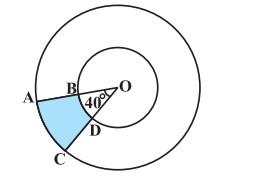
हल:
दिया है, बड़े वृत्त की त्रिज्या (r₁) = 14 cm और छोटे वृत्त की त्रिज्या (r₂) = 7 cm
त्रिज्यखण्ड का कोण (θ) = 40°
छायांकित भाग का क्षेत्रफल
= त्रिज्यखण्ड OAC का क्षेत्रफल – त्रिज्यखण्ड OBD का क्षेत्रफल

प्रश्न 3. दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 cm का एक वर्ग है तथा APP और BPC दो अर्द्धवृत्त हैं।

हल:
दिया है, वर्ग ABCD की भुजा = 14 cm
वर्ग ABCD का क्षेत्रफल = भुजा2 = 14 × 14 cm² = 196 cm²
अर्द्धवृत्तों का व्यास = वर्ग ABCD की भुजा
2 × त्रिज्या = 14
⇒ त्रिज्या (r) = 7 cm

= 154 cm²
चित्र से स्पष्ट है कि छायांकित भाग का क्षेत्रफल = वर्ग ABCD का क्षेत्रफल – दोनों अर्द्धवृत्तों का क्षेत्रफल
= 196 cm² – 154 cm²
= 42 cm²
अत: छायांकित भाग का क्षेत्रफल = 42 cm²

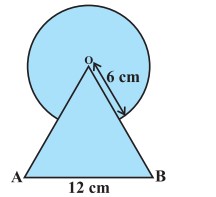
प्रश्न 4. दी गई आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ भुजा 12 cm वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केन्द्र मानकर 6 cm त्रिज्या वाला एक वृत्तीय चाप खींचा गया है।

हल:
दिया है, समबाहु त्रिभुज की भुजा = 12 cm
हम जानते हैं कि समबाहु ΔOAB का क्षेत्रफल
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.3 Q4.1
दीर्घ त्रिज्यखण्ड का कोण, θ = 360° – 60° = 300°
(∵ समबाहु त्रिभुज का अन्त:कोण 60° का होता है।)
दिया है, वृत्त की त्रिज्या (r) = 6 cm
दीर्घ त्रिज्यखण्ड का क्षेत्रफल
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.3 Q4.2
छायांकित भाग का सम्पूर्ण क्षेत्रफल = दीर्घ त्रिज्यखण्ड का क्षेत्रफल + समबाहु त्रिभुज का क्षेत्रफल

प्रश्न 5. भुजा 4 cm वाले एक वर्ग के प्रत्येक कोने से 1 cm त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है तथा बीच में 2 cm व्यास का एक वृत्त भी काटा गया है जैसा कि आकृति में दर्शाया गया है। वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए।

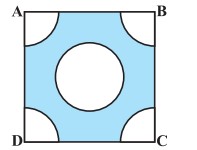
हल:
ABCD एक वर्ग है जिसकी प्रत्येक भुजा 4 cm है।
वर्ग का क्षेत्रफल = 4 × 4 = 16 m²
दिया है, वृत्त के एक चतुर्थांश की त्रिज्या (r) = 1 cm

छायांकित भाग का क्षेत्रफल = वर्ग का क्षेत्रफल – (चारों चतुर्थांशों का क्षेत्रफल + वृत्त का क्षेत्रफल)
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.3 Q5.1

प्रश्न 6. एक वृत्ताकार मेजपोश, जिसकी त्रिज्या 32 cm है, के बीच में एक समबाहु त्रिभुज ABC छोड़ते हुए एक डिजाइन बना हुआ है, जैसा कि आकृति में दिखाया गया है। इस छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए।

हल:
∆ABC एक समबाहु त्रिभुज है।
∠B = 60°
OB तथा OC वृत्ताकार मेजपोश की त्रिज्याएँ हैं।
OB = 32 cm

प्रश्न 7. दी गई आकृति में, ABCD भुजा 14 cm वाला एक वर्ग है। A, B, C और D को केन्द्र मानकर, चार वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त तीन शेष वृत्तों में से दो वृत्तों को बाह्य रूप से स्पर्श करता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल:
दिया है, वर्ग ABCD की भुजा = 14 cm
अर्थात् AB = BC = CD = DA = 14 cm
वर्ग ABCD का क्षेत्रफल = (भुजा)² = 14 × 14 = 196 cm²
चित्र से स्पष्ट है कि चारों वृत्तों के चतुर्थांश वर्ग ABCD में समाहित हैं।
चारों वृत्त-चतुर्थांशों का क्षेत्रफल = एक वृत्त का क्षेत्रफल

छायांकित भाग का क्षेत्रफल = वर्ग ABCD का क्षेत्रफल – चारों वृत्तीय चतुर्थांशों का क्षेत्रफल
= (196 – 154) cm²
= 42 cm²
अतः छायांकित भाग का क्षेत्रफल = 42 cm²

प्रश्न 8. आकृति एक दौड़ने का पथ (racing track) दर्शाती है, जिसके बाएँ और दाएँ सिरे अर्द्धवृत्ताकार हैं।

दोनों आन्तरिक समान्तर रेखाखण्डों के बीच की दूरी 60 m है तथा इनमें से प्रत्येक रेखाखण्ड 106 m लम्बा है। यदि यह पथ 10 m चौड़ा है, तो ज्ञात कीजिए :
(i) पथ के आन्तरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दूरी
(ii) पथ का क्षेत्रफल।
हल
(i) दिया है, अर्द्धवृत्ताकार पथों की आन्तरिक त्रिज्या (r’) = 60/2 m = 30 m

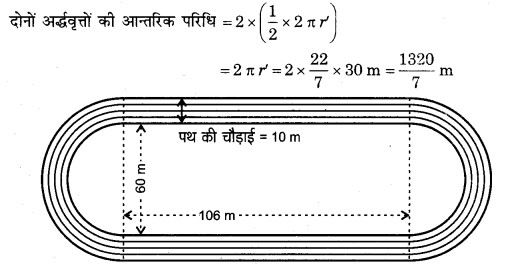
दिया है, प्रत्येक रेखाखण्ड की लम्बाई = 106 m
दोनों आन्तरिक समान्तर रेखाखण्डों की लम्बाई = 106 m + 106 m = 212 m.
पथ के आन्तरिक किनारों के अनुदिश 1 चक्कर की लम्बाई = दोनों अर्द्धवृत्तों की आन्तरिक परिधि + दोनों आन्तरिक समान्तर रेखाखण्डों की लम्बाई
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.3 Q8.2
अत: पथ के आन्तरिक किनारों के अनुदिश 1 पूरा चक्कर लगाने में चली गई दूरी = 2804/7 m

(ii) वृत्ताकार पथ भागों की आन्तरिक त्रिज्या (r’) = 30 m और पथ चौड़ाई = 10 m
वृत्ताकार पथ भागों की बाह्य त्रिज्या r = (30 + 10) m = 40 m
दोनों वृत्ताकार भागों का क्षेत्रफल = π(r² – r’²)
= π(r + r’) (r – r’)
= π(40 + 30) (40 – 30)
= $\frac { 22 }{ 7 }$ × 70 × 10
= 2200 m²
वृत्ताकार भागों के अतिरिक्त पथ का क्षेत्रफल = 2 × (लम्बाई × पथ की चौड़ाई)
= 2 × (106 × 10)
= 2120 m²
पथ का कुल क्षेत्रफल = (2200 + 2120) m² = 4320 m²
अत: पथ का क्षेत्रफल = 4320 m²

प्रश्न 9. आकृति में, AB और CD केन्द्र O वाले एक वृत्त के दो परस्पर व्यास हैं तथा OD छोटे वृत्त का व्यास है। यदि OA = 7 cm है तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल:
बड़े वृत्त की त्रिज्या OA = OD = छोटे वृत्त का व्यास
छोटे वृत्त का व्यास = OD = OA = 7 cm

= OA²
= (7)²
= 49 cm
अर्द्धवृत्त AOBCA के छायांकित भाग का क्षेत्रफल = (77 – 49) cm² = 28 cm²
अतः सम्पूर्ण छायांकित भाग का क्षेत्रफल = (छोटे वृत्त का क्षेत्रफल + अर्द्धवृत्त AOBCA के छायांकित भाग का क्षेत्रफल
= (38.5 + 28)
= 66.5 cm²

प्रश्न 10. एक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 cm² है। इस त्रिभुज के प्रत्येक शीर्ष को केन्द्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 और √3 = 1.73205 लीजिए)

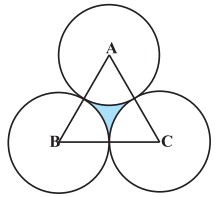
हल:
माना वृत्तों की त्रिज्याएँ r cm हैं।
समबाहु त्रिभुज की भुजा = वृत्त का व्यास = 2r cm

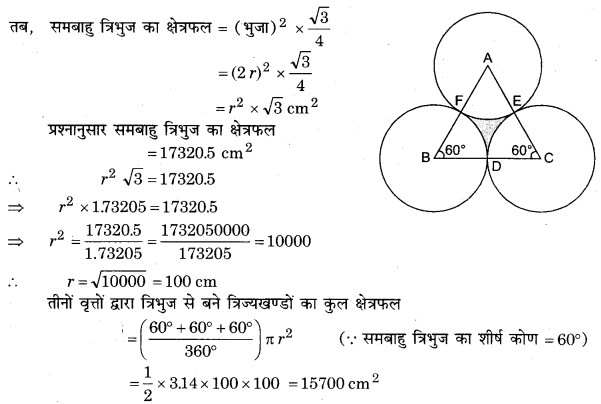
समबाहु त्रिभुज का क्षेत्रफल = 17320.5 cm²
अतः त्रिभुज के उस भाग का क्षेत्रफल जो वृत्तों के अन्दर नहीं है = समबाहु त्रिभुज का क्षेत्रफल – त्रिज्यखण्डों का कुल क्षेत्रफल
= 17320.5 – 15700
= 1620.5 cm²

प्रश्न 11. एक वर्गाकार रूमाल पर नौ वृत्ताकार डिजाइन बने हैं, जिनमें से प्रत्येक की त्रिज्या 7 cm है (आकृति देखिए)। रूमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए।

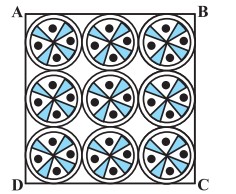
हल:
दिया है, प्रत्येक वृत्त की त्रिज्या (r) = 7 cm
प्रत्येक वृत्त का क्षेत्रफल = πr²
= $\frac { 22 }{ 7 }$ × 7 × 7 cm²
= 154 cm²
नौ वृत्ताकार डिजाइनों का क्षेत्रफल = 9 × 154 = 1386 cm²
प्रत्येक वृत्त का व्यास = 2 × 7 = 14 cm
दिए गए चित्र में, प्रत्येक पंक्ति में 3 वृत्त हैं।
वर्गाकार रूमाल की लम्बाई = 3 x एक वृत्त का व्यास = 3 × 14 = 42 cm
वर्गाकार रूमाल का कुल क्षेत्रफल = 42 × 42 cm² = 1764 cm²
रूमाल के शेष भाग का क्षेत्रफल = रूमाल का कुल क्षेत्रफल – 9 वृत्ताकार डिजाइनों का क्षेत्रफल
= (1764 – 1386) cm²
= 378 cm²
अतः रूमाल के शेष भाग का क्षेत्रफल = 378 cm²

प्रश्न 12. दी गई आकृति में, OACB केन्द्र O और त्रिज्या 3.5 cm वाले एक वृत्त का चतुर्थांश है। यदि OD = 2 cm है तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
(i) चतुर्थांश OACB
(ii) छायांकित भाग।

हल:
दिया है, वृत्ताकार चतुर्थांश की त्रिज्या (r) = 3.5 cm, OD = 2 cm

प्रश्न 13. दी गई आकृति में, एक चतुर्थांश OPBQ के अन्तर्गत एक वर्ग OABC बना हुआ है। यदि OA = 20 cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)

हल:
दिया है, वर्ग OABC की भुजा, OA = 20 cm
वर्ग OABC का विकर्ण, OB = भुजा√2 = OA√2 = 20√2 cm
चतुर्थांश OPBQ की त्रिज्या (r) = OB = 20√2 cm
चतुर्थांश OPBQ का क्षेत्रफल = ¼πr2
= ¼ × 3.14 × (20√2)²
= ¼ × 3.14 × 20√2 × 20√2
= 628 cm²
और वर्ग OABC का क्षेत्रफल = (भुजा)² = (OA)² = (20)² = 400 cm²
अंत: छायांकित भाग का क्षेत्रफल = (चतुर्थाश OPBQ का क्षेत्रफल – वर्ग OABC का क्षेत्रफल)
= 628 – 400
= 228 cm²

प्रश्न 14. AB और CD केन्द्र O तथा त्रिज्याओं 21 cm और 7 cm वाले दो संकेन्द्रीय वृत्तों के क्रमशः दो चाप हैं (आकृति देखिए) यदि ∠AOB = 30° है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल:
दिए गए चित्र में,
त्रिज्यखण्ड OBAO की लम्बाई (r₁) = 21 cm
तथा त्रिज्यखण्ड OCDO की लम्बाई (r₂) = 7 cm
माना संकेन्द्रीय वृत्तों का त्रिज्यकोण (θ) = 30°
त्रिज्यखण्ड ORAO का क्षेत्रफल
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Ex 12.3 Q14.1
त्रिज्यखण्ड OCDO का क्षेत्रफल

अत: छायांकित भाग का क्षेत्रफल = दोनों त्रिज्यखण्डों के क्षेत्रफलों का अन्तर
= (त्रिज्यखण्ड OBAO का क्षेत्रफल – त्रिज्यखण्ड OCDO का क्षेत्रफल)

प्रश्न 15. दी गई आकृति में, ABC त्रिज्या 14 सेमी वाले एक वृत्त का चतुर्थांश है तथा BC को व्यास मानकर एक अर्द्धवृत्त खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल:
दिया है, चतुर्थांश ABC की त्रिज्या (r) = 14 cm

= 154 cm²
छायांकित भाग का क्षेत्रफल = BC व्यास वाले अर्द्धवृत्त का क्षेत्रफल – (चतुर्थांश ABC का क्षेत्रफल – समकोण ΔABC का क्षेत्रफल)
= समकोण ∆ABC का क्षेत्रफल + अर्द्धवृत्त का क्षेत्रफल – चतुर्थांश ABC का क्षेत्रफल
= (98 + 154 – 154) cm²
= 98 cm²
अत: छायांकित भाग का क्षेत्रफल = 98 cm²

प्रश्न 16. दी गई आकृति में, छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 cm त्रिज्याओं वाले दो वृत्तों के चतुर्थांशों के बीच उभयनिष्ठ है।

हल:
ध्यान दीजिए दो समान त्रिज्यखण्डों को मिलाने 8 सेमी पर दी गई आकृति प्राप्त होती है और लूप परस्पर आच्छादित करते हैं।
दिया है, चतुर्थांशों की त्रिज्याएँ (r) = 8 cm
तथा चतुर्थांश का कोण (θ) = 90°
एक चतुर्थांश का क्षेत्रफल

वृतों से संबंधित क्षेत्रफल Additional Questions

बहुविकल्पीय प्रश्न

प्रश्न 1.
यदि R₁ और R₂ त्रिज्याओं वाले दो वृत्तों की परिधियों का योग त्रिज्या R वाले एक वृत्त की परिधि के बराबर हो, तो
(i) R₁ + R₂ = R
(ii) R₁ + R₂ > R
(iii) R₁ + R₂ < R
(iv) R₁, R₂ और R के बीच सम्बन्ध के बारे में निश्चित रूप से कुछ नहीं कहा जा सकता।
हल
(i) R₁ + R₂ = R

प्रश्न 2.
यदि एक वृत्त की परिधि और एक वर्ग का परिमाप बराबर है, तो
(i) वृत्त का क्षेत्रफल = वर्ग का क्षेत्रफल
(ii) वृत्त का क्षेत्रफल > वर्ग का क्षेत्रफल
(iii) वृत्त का क्षेत्रफल < वर्ग का क्षेत्रफल
(iv) वृत्त और वर्ग के क्षेत्रफलों के बीच के सम्बन्ध में निश्चित रूप से नहीं कहा जा सकता।
हल
(ii) वृत्त का क्षेत्रफल > वर्ग का क्षेत्रफल

प्रश्न 3.
त्रिज्या r के अर्धवृत्त के अन्तर्गत खींचे जा सकने वाले सबसे बड़े त्रिभुज का क्षेत्रफल है
(i) r²
(ii) 1/2 r²
(iii) 2r²
(iv) √2r²
हल
(i) r²

प्रश्न 4.
यदि एक वृत्त का परिमाप का एक वर्ग के परिमाप के बराबर है, तो उनके क्षेत्रफलों का अनुपात है
(i) 22 : 7
(ii) 14 : 11
(iii) 7 : 22
(iv) 11 : 14
हल
(ii) 14 : 11

प्रश्न 5.
किसी स्थान पर 16 m और 12 m व्यास वाले दो वृत्ताकार पार्को के क्षेत्रफलों के योग के बराबर क्षेत्रफल का एक अकेला साकार पार्क बनाने का प्रस्ताव है। नये पार्क की त्रिज्या होगी।
(i) 10 m
(ii) 15 m
(iii) 20 m
(iv) 24 m
हल
(i) 10 m

प्रश्न 6.
भुजा 6 cm वाले एक वर्ग के अन्तर्गत खींचे जा सकने वाले वृत्त का क्षेत्रफल है
(i) 36π cm²
(ii) 18π cm²
(iii) 12π cm²
(iv) 9π cm²
हल
(iv) 9π cm²

प्रश्न 7.
त्रिज्या 8 cm वाले एक वृत्त के अन्तर्गत खींचे जा सकने वाले वर्ग का क्षेत्रफल है
(i) 256 cm²
(ii) 128 cm²
(iii) 64√2 cm²
(iv) 64 cm²
हल
(ii) 128 cm²

प्रश्न 8.
व्यासों 36 cm और 20 cm वाले दो वृत्तों की परिधियों के योग के बराबर परिधि वाले एक वृत्त की त्रिज्या है.
(i) 56 cm
(ii) 42 cm
(iii) 28 cm
(iv) 16 cm
हल
(iii) 28 cm

प्रश्न 9.
त्रिज्याओं 24 cm वाले और 7 cm वाले दो वृत्तों के क्षेत्रफलों के योग के बराबर क्षेत्रफल वाले एक वृत्त का व्यास है।
(i) 31 cm
(ii) 25 cm
(iii) 62 cm
(iv) 50 cm
हल
(iv) 50 cm

प्रश्न 10.
यदि एक वृत्त का क्षेत्रफल 154 cm² हैं, तो उसका परिमाप है
(i) 11 cm
(ii) 22 cm
(iii) 44 cm
(iv) 55 cm
हल
(iii) 44 cm

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
7 cm त्रिज्या वाले वृत्त के एक त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए जिसका कोण 90° है।
हल
दिया है, वृत्त की त्रिज्या = 7 cm
तथा त्रिज्यखण्ड कोण, (θ) = 90°
त्रिज्यखण्ड का क्षेत्रफल

प्रश्न 2.
दो वृत्तों की परिधियों का अनुपात 2 : 3 है, उनकी त्रिज्याओं का अनुपात ज्ञात कीजिए।
हल
माना वृत्तों की त्रिज्याएँ क्रमशः r₁ तथा r₂ हैं, तब इनकी परिधियाँ क्रमश: 2πr₁ तथा 2πr₂ होंगी।
प्रश्नानुसार, परिधियों का अनुपात = 2 : 3
⇒ 2πr₁ : 2πr₂ = 2 : 3
⇒ r₁ : r₂ = 2 : 3
अत: त्रिज्याओं का अनुपात 2 : 3 है।

प्रश्न 3.
आकृति में, चाप AB की लम्बाई सेमी में ज्ञात कीजिए।

हल
दिया है, OA = OB = 28 cm तथा θ = 45°

लघु उत्तरीय प्रश्न

प्रश्न 1.
21 सेमी त्रिज्या वाले एक वृत्त का चाप केन्द्र पर 120° का कोण अन्तरित करता है। चाप द्वारा बने त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हल
दिया है, वृत्त की त्रिज्या (r) = 21 cm
त्रिज्यखण्ड का कोण (θ) = 120°
त्रिज्यखण्ड का क्षेत्रफल

अत: चाप द्वारा बने त्रिज्यखण्ड का क्षेत्रफल = 462 cm²

प्रश्न 2.
आकृति में, 35 m त्रिज्या वाले एक वृत्ताकार बाग का केन्द्र O है। इसके छायांकित भाग में पत्थर बिछाने का व्ययर 75.0 प्रति वर्ग मीटर की दर से ज्ञात कीजिए ∠AOB = 120° है।

हल
दिया है, r = 35 m तथा θ = 120°
त्रिज्यखण्ड (छायांकित भाग) का क्षेत्रफल

अतः पत्थर बिछाने का व्यय = ₹ 96250

प्रश्न 3.
त्रिज्या 4 cm वाले एक वृत्त के त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60° है। संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल भी ज्ञात कीजिए। (π = 3.14)

हल
दिया है, त्रिज्या (r) = 4 cm तथा त्रिज्याखण्ड का कोण (θ) = 60°

= 8.37 cm²
संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल = (वृत्त का क्षेत्रफल – त्रिज्यखण्ड OAPBO का क्षेत्रफल)
= πr² – 8.37
= 3.14 × 4 × 4 – 8.37
= 50.24 – 8.37
= 41.87 cm²
अत: वृत्त के त्रिज्यखण्ड का क्षेत्रफल = 8.37 cm²
तथा संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल = 41.87 cm²

प्रश्न 4.
संलग्न आकृति में छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए, जहाँ ABCD भुजा 14 cm का एक वर्ग है।

हल
दिया है, वर्ग की भुजा = 14 cm
वर्ग ABCD का क्षेत्रफल = (14 × 14) cm² = 196 cm²

अतः छायांकित क्षेत्र का क्षेत्रफल = (196 – 154) cm² = 42 cm²

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
आकृति में, AB और CD केन्द्र O तथा त्रिज्याओं 15 सेमी वाले दो सकेन्द्रीय वृत्तों के क्रमशः दो चाप हैं, यदि ∠AOB = 60°, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल

अतः छायांकित भाग का क्षेत्रफल 99 cm² है।

प्रश्न 2.
दी गई आकृति से लघु वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए यदि ∠AOB = 120° और वृत्त की त्रिज्या OA = 21 cm

हल
दिया है, वृत्त की त्रिज्या (R) = OA = 21 cm और θ = ∠AOB = 120°
त्रिज्यखण्ड AOBA का क्षेत्रफल
Bihar Board Class 10 Maths Solutions Chapter 12 वृतों से संबंधित क्षेत्रफल Additional Questions LAQ 2.1
∆OAB के क्षेत्रफल के लिए :

∆OAB में, OA = OB
अर्थात् ∆OAB समद्विबाहु त्रिभुज है
शीर्ष O से AB पर लम्ब OD खींचा जो AB को समद्विभाजित करेगा, क्योंकि AB वृत्त की जीवा भी है और लम्ब OD वृत्त के केन्द्र से जाता है।
तब, ∆OAD में, ∠AOD = 60° और ∠OAD = 30° तथा ∠ADO = 90°
समकोण ∆OAD में,

अब, लघु वृत्तखण्ड का क्षेत्रफल = त्रिज्यखण्ड AOBA का क्षेत्रफल – ∆OAB का क्षेत्रफल
= (462 – 441/4 √3) cm²
= (462 – 110.25 × √3) cm²
= (462 – 110.25 × 1.732) cm²
= (462 – 190.953) cm²
= 271.047 cm²
अत: लघु वृत्तखण्ड का क्षेत्रफल = 271.047 cm²