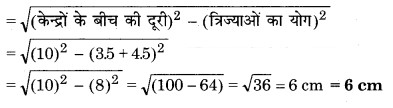bihar board class 10th maths | Constructions (रचनाएँ)

Bihar Board Solutions for Class 10 Maths Chapter 11 Constructions (रचनाएँ)

प्रश्नावली 11.1

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिएः

प्रश्न 1. 7.6 cm लम्बा एक रेखाखण्ड खींचिए और इसे 5 : 8 के अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
हल:
दिया है : रेखाखण्ड AB = 7.6 cm
रचना करनी है : रेखा AB को 5 : 8 में विभाजित करने की।
रचना विधि :
1. रेखाखण्ड AB = 7.6 cm खींचा।
2. रेखाखण्ड AB पर बिन्दु A से न्यूनकोण बनाती हुई एक ऋजु रेखा AX खींची।

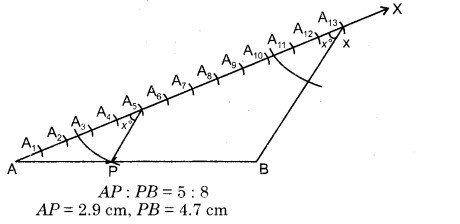
3. रेखा AX में से समान लम्बाई के (5 + 8 = 13) भाग AA₁, A₁A₂, A₂A₃, A₃A₄, A₄A₅, A₅A₆, A₆A₇, A₇A₈, A₈A₉, A₉A₁₀, A₁₀A₁₁, A₁₁A₁₂ व A₁₂A₁₃ खण्ड काटे।
4. रेखाखण्ड AB खींचा।
5. बिन्दु A₅ से A₁₃B के समान्तर रेखा A₅P खींची जो AB को बिन्दु P पर काटती है।
AP तथा PB, रेखाखण्ड AB के अभीष्ट भाग हैं जो 5 : 8 के अनुपात में हैं।
औचित्य ( उपपत्ति) :
∆AA₅P तथा ∆AA₁₃B में A₅P || A₁₃B
अतः ये त्रिभुज परस्पर समरूप हैं।
∴ AA₅ : A₅A₁₃ = AP : PB
परन्तु AA₅ : A₅A₁₃ = 5 : 8
∴ AP : PB = 5 : 8
मापने पर : AP = 2.9 cm व PB = 4.7 cm

प्रश्न 2. 4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की  गुनी हों।
हल: 
दिया है : ∆ABC में भुजा AB = 4.0 cm, BC = 5.0 cm तथा CA = 6.0 cm
रचना करनी है : ∆ABC के समरूप एक ∆A’BC’ की जिसकी प्रत्येक भुजा ∆ABC की संगत भुजा की  हो।
रचना विधि :
1. ऋजु रेखा BC = 5.0 cm खींची।
2. B को केन्द्र मानकर 4.0 cm त्रिज्या से और C को केन्द्र मानकर 6.0 cm त्रिज्या से चाप लगाए जो परस्पर A पर काटते हैं।

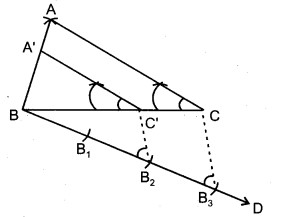
3. ऋजु रेखाओं AB तथा AC को पूरा किया।
4. B से एक ऋजु रेखा BD खींचकर उसमें से BB₁, BB₂, BB₃ तीन समान भाग काटे।
5. ऋजु रेखा CB₃ खींची।
6. B₂ से CB₃ के समान्तर ऋजु रेखा C’B₂ खींची जिससे
BC’ =  BC
7. C’ से CA के समान्तर ऋजु रेखा C’A’ खींची जो AB को A’ पर मिलती है जिससे
A’B =  AB
∆A’BC’अभीष्ट समरूप त्रिभुज है।
औचित्य : ∆BB₂C’ व ∆BB₃C में, B₂C’ || B₃C
ये त्रिभुज समरूप हैं,
BC’ : BC = BB₂ : BB₃
परन्तु BB₂ : BB₃ = 2 : 3
BC’ : BC = 2 : 3
⇒ BC’ =  BC
इसी प्रकार ∆BC’A’ व ∆BCA समरूप हैं।
BA’ : BA = C’A’ : CA = BC’ : BC = 2 : 3
अत: ∆BC’A’ दिए गए त्रिभुज के समरूप है जिसकी भुजाएँ मूल त्रिभुज की भुजाओं की हैं।

प्रश्न 3. 5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की  गुनी हों।
हल: दिया है : 5 cm, 6 cm, 7 cm भुजाओं वाला एक त्रिभुज।
रचना करनी है : उपर्युक्त त्रिभुज के समरूप एक अन्य त्रिभुज की जिसकी प्रत्येक भुजा दिए त्रिभुज की प्रत्येक संगत भुजा का  वाँ भाग हो।
रचना विधि :
1. रेखाखण्ड BC = 6 cm खींचा।
2. B को केन्द्र मानकर 5 cm त्रिज्या से एवं C को केन्द्र मानकर 7 cm त्रिज्या के चाप खींचे जो परस्पर A पर काटते हैं।
3. रेखाखण्ड AB तथा AC खींचकर दिया हुआ त्रिभुज ABC प्राप्त किया।
4. बिन्दु B से रेखा BD खींची और उसमें से BB₁, B₁B₂, B₂B₃, B₃B₄, B₄B₅, B₅B₆ तथा B₆B₇ सात समान भाग काटे।

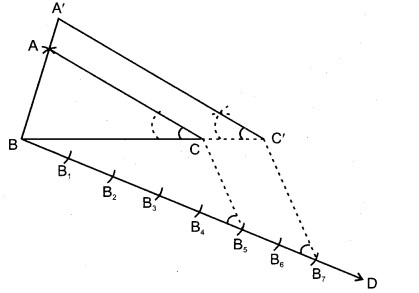
5. रेखाखण्ड CB खींचा।
6. B₇ से रेखा B₇C’ || B₅C खींची जो BC को बढ़ाने पर C’ पर काटती है जिससे BC’ =  BC
7. C’ से C’A’ || CA खींची जो BA को बढ़ाने पर इसे A पर काटे जिससे A’B =  AB
∆A’BC’ अभीष्ट समरूप त्रिभुज है।
औचित्य : ∆BB₂C’ व ∆BB₃C में, B₂C’ || B₃C
ये त्रिभुज समरूप हैं,
BC’ : BC = BB₂ : BB₃
परन्तु BB₂ : BB₃ = 7 : 5
BC’ : BC = 7 : 5
⇒ BC’ =  BC
इसी प्रकार ∆BC’A’ व ∆BCA समरूप हैं।
BA’ : BA = C’A’ : CA = BC’ : BC = 7 : 5
अत: ∆BC’A’ दिए गए त्रिभुज के समरूप है जिसकी भुजाएँ मूल त्रिभुज की भुजाओं की हैं।

प्रश्न 4. आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 1 गुनी हों।
हल:
दिया है : 8 cm आधार और 4 cm ऊँचाई का एक समद्विबाहु त्रिभुज।
रचना करनी है : उक्त समद्विबाहु त्रिभुज की और एक अन्य त्रिभुज की जिसकी भुजाएँ दिए हुए समद्विबाहु त्रिभुज की संगत भुजाओं की 3/2 हों।
रचना विधि :
1. रेखाखण्ड AB = 8 cm खींचा।
2. रेखाखण्ड AB का लम्ब समद्विभाजक खींचा जो AB को M पर काटता है।
3. M को केन्द्र मानकर समद्विभाजक में से MA = 4 cm काटा।
4. रेखाखण्ड AB व AC खींचकर समद्विबाहु त्रिभुज ABC प्राप्त किया।

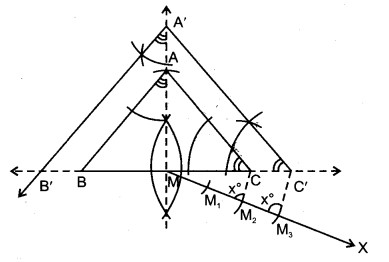
5. BC को दोनों ओर बढ़ाया।
6. बिन्दु M पर BC से नीचे की ओर न्यूनकोण बनाती हुई रेखा MX खींची।
7. MX में से 3 समान भाग MM₁, M₁M₂, M₂M₃ खींचे।
8. रेखाखण्ड M₂C खींचा और M₃ से M₂C के समान्तर रेखा खींची जो बढ़ी हुई BC में C’ पर मिलती है।
9. C’ से AC के समान्तर C’A’ खींची जो MA से बिन्दु A’ पर मिलती है।
10. अब A से AB के समान्तर AB’ खींची जो बढ़ी हुई CB से B’ पर मिलती है।
ΔABC’ अभीष्ट त्रिभुज है।
औचित्य : ∆BB₂C’ व ∆BB₃C में, B₂C’ || B₃C
ये त्रिभुज समरूप हैं,
BC’ : BC = BB₂ : BB₃
परन्तु BB₂ : BB₃ = 3 : 2
BC’ : BC = 3 : 2
⇒ BC’ = 3/2 BC
इसी प्रकार ∆BC’A’ व ∆BCA समरूप हैं।
BA’ : BA = C’A’ : CA = BC’ : BC = 3 : 2
अत: ∆BC’A’ दिए गए त्रिभुज के समरूप है जिसकी भुजाएँ मूल त्रिभुज की भुजाओं की 3/2 हैं।

प्रश्न 5. एक त्रिभुज ABC बनाइए जिसमें BC = 6 सेमी, AB = 5 सेमी. और ∠ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की गुनी हों। [CBSE Sample Paper2011]
हलः
दिया है : एक त्रिभुज ABC जिसकी भुजा AB = 5 cm, BC = 6 cm और ∠ABC = 60° हैं।
रचना करनी है : एक अन्य त्रिभुज की जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 3/2 गुनी हों।
रचना विधि :
1. रेखाखण्ड BC = 6 cm खींचा।
2. BC के बिन्दु B पर BC से 60° का B कोण बनाती हुई रेखा BY खींची।
3. BY में से AB = 5 cm काटी और रेखाखण्ड AC को खींचकर त्रिभुज ABC प्राप्त किया।

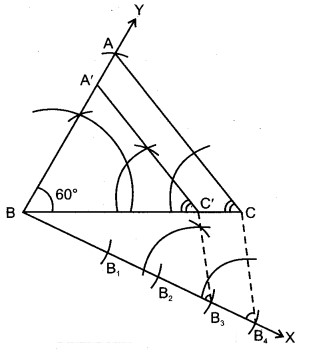
4. BC के दूसरी ओर बिन्दु B से BC पर न्यूनकोण बनाती हुई रेखा BX खींची।
5. BX में से चार समान भाग BB₁, B₁B₂, B₂B₃ और B₃B₄ खींचे।
6. B₄C खींची और B₃ से B₄C के समान्तर एक रेखा खींची जो BC से C” पर मिलती है।
7. C’ से AC के समान्तर रेखा C’A’ खींची जो AB से A’ पर मिलती है।
∆A’BC’ अभीष्ट त्रिभुज है।
औचित्य : ∆BB₂C’ व ∆BB₃C में, B₂C’ || B₃C
ये त्रिभुज समरूप हैं,
BC’ : BC = BB₂ : BB₃
परन्तु BB₂ : BB₃ = 3 : 4
BC’ : BC = 3 : 4
⇒ BC’ =  BC
इसी प्रकार ∆BC’A’ व ∆BCA समरूप हैं।
BA’ : BA = C’A’ : CA = BC’ : BC = 3 : 4
अत: ∆BC’A’ दिए गए त्रिभुज के समरूप है जिसकी भुजाएँ मूल त्रिभुज की भुजाओं की  हैं।

प्रश्न 6. एक त्रिभुज ABC बनाइए जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की गुनी हों।
हलः
दिया है : ∆ABC जिसमें BC = 7 cm, ∠B = 45° व ∠A = 105°
रचना करनी है : एक अन्य त्रिभुज की जिसकी भुजाएँ ∆ABC की संगत भुजाओं की  गुनी हो।
रचना विधि :
1. रेखाखण्ड BC =7 cm खींचा।
2. BC के बिन्दु B पर BC से 45° का कोण बनाती हुई एक रेखा BZ खींची।
3. BC के दूसरी ओर B पर BC से 105° के कोण पर रेखा BD खींची।
4. BD के बिन्दु B पर BD से समकोण बनाती हुई एक रेखा BX खींची।
5. BC का लम्ब समद्विभाजक खींचा जो Bx को बिन्दु O पर काटती है।
6. O को केन्द्र मानकर OB त्रिज्या से वृत्तखण्ड BAC खींचा जो BZ को बिन्दु A पर काटता है।
7. AC को मिलाकर ∆ABC प्राप्त किया।

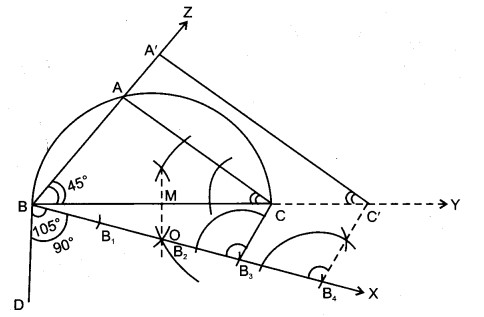
8. BX में से 4 समान खण्ड BB₁, B₁B₂, B₂B₃ व B₃B₄ खींचे।
9. रेखाखण्ड B₃C खींचा।
10. बिन्दु B₄ से B₄C’ समान्तर BC खींची जो बढ़ी हुई BC को C’ पर काटती है।
11. C’ से C’A’ समान्तर AC खींची जो BZ को A’ पर काटती है।
∆A’BC’ अभीष्ट त्रिभुज है।

प्रश्न 7. एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 सेमी. तथा 3 सेमी. लम्बाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की गुनी हों।
हलः
दिया है : समकोण त्रिभुज जिसकी समकोण बनाने वाली भुजाएँ 3 cm व 4 cm हों।
रचना करनी है : एक अन्य त्रिभुज की जिसकी भुजाएँ उक्त समकोण त्रिभुज की संगत भुजाओं की  गुनी हों।
रचना विधि :
1. रेखाखण्ड BC = 4 cm खींचा।
2. BC के बिन्दु B से BC पर लम्ब BY खींचा और उसमें से BA (या AB) = 3 cm काटी।
3. AC को मिलाया। इस प्रकार ∆ABC प्राप्त होगा।
4. BC के बिन्दु B पर BC से न्यूनकोण बनाती हुई रेखा BX खींची।
5. BX में से 5 समान भाग BB₁, B₁B₂, B₂B₃, B₃B₄ व B₄B₅ काटी।
6. B₃C को मिलाया।

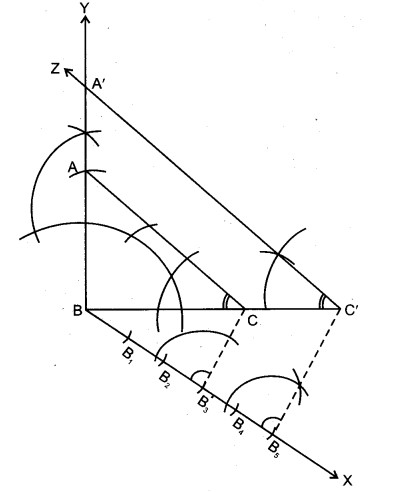
7. B₅ से B₅C के समान्तर रेखा B₅C’ खींची जो बढ़ी हुई BC से C’ पर मिलती है।
8. C’ से C’A’ || CA खींची जो BY से A’ पर मिलती है।
∆A’BC’अभीष्ट त्रिभुज है।
औचित्य : ∵ BB₅, BB₃ की  गुनी है और B₃C || B₅C
BC’ = BC और BC’ =  BC
तथा AC || AC’
A’B =  AB
अतः भुजाएँ A’B, BC’ व C’A’ क्रमश: AB, BC व CA की  गुनी है।

प्रश्नावली 11.2

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिएः

प्रश्न 1. 6 cm त्रिज्या का एक वृत्त खींचिए। केन्द्र से 10 cm दूर एक बिन्दु से वृत्त पर स्पर्श रेखा-युग्म की रचना कीजिए और उनकी लम्बाइयाँ मापकर लिखिए।
हल: दिया है : 6 cm त्रिज्या का एक वृत्त और उसके केन्द्र O से 10 cm दूरी पर एक बिन्दु P.
रचना करनी है : वृत्त के स्पर्श रेखा-युग्म की।
रचना विधि :
1. सर्वप्रथम बिन्दु O को केन्द्र मानकर 6 cm त्रिज्या का एक वृत्त खींचा।
2. वृत्त के केन्द्र O से 10 cm की दूरी पर एक बिन्दु P लिया।
3. OP को मिलाया।
4. OP को व्यास मानकर एक वृत्त खींचा जिसने केन्द्र O वाले वृत्त को T₁ और T₂ बिन्दुओं पर काटा।
5. PT₁ और PT₂ को मिलाया जो वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।

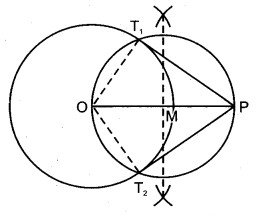
मापने पर : PT₁ = PT₂ = 8.0 cm
उपपत्ति : रेखाखण्ड OT₁ व OT₂ खींचिए।
∵ OP व्यास है।
∴ OT₁P तथा OT₂P अर्द्धवृत्त हैं
∵ ∠OT₁P, अर्द्धवृत्त OT₁P में तथा ∠OT₂P, अर्द्धवृत्त ∠OT₂P में स्थित हैं।
∠OT₁P = 90° तथा ∠OT₂P = 90°
∵ OT₁ और OT₂, केन्द्र O वाले वृत्त की त्रिज्याएँ हैं जिनके सिरों T₁ व T₂ पर T₁P तथा T₂P समकोण बनाती हैं।
अत: PT₁ तथा PT₂ स्पर्श रेखाएँ हैं।

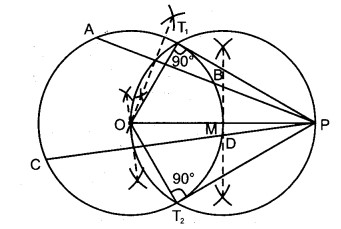
प्रश्न 2. 4 cm त्रिज्या के एक वृत्त पर 6 cm त्रिज्या के एक संकेन्द्रीय वृत्त के किसी बिन्दु से एक स्पर्श रेखा की रचना कीजिए और उसकी लम्बाई मापिए। परिकलन से इस माप की जाँच भी कीजिए।
हल: दिया है : 4 cm त्रिज्या का एक वृत्त और 6 cm त्रिज्या का एक संकेन्द्रीय वृत्त जिस पर एक बिन्दु P है।
रचना करनी है : 4 cm त्रिज्या वाले वृत्त की स्पर्श रेखाओं की।
रचना विधि :
1. 4 cm त्रिज्या लेकर केन्द्र O वाला एक वृत्त खींचा।
2. केन्द्र O से 6 cm त्रिज्या का एक संकेन्द्रीय वृत्त खींचा और इस पर एक बिन्दु लिया।
3. रेखाखण्ड OP खींचा और इसका लम्ब समद्विभाजक खींचा जो OP को बिन्दु M पर काटता है।
4. केन्द्र M से OP व्यास का एक वृत्त खींचा जो केन्द्र O के 4 cm त्रिज्या वाले वृत्त को T₁ तथा T₂ पर काटता है।
5. रेखाखण्ड PT₁ तथा PT₂ खींचा।

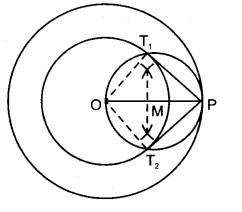
PT₁ तथा PT₂ अभीष्ट स्पर्श रेखाएँ हैं।
मापने पर : PT₁ = 4.5 cm तथा PT₂ = 4.5 cm
परिकलन :

औचित्य : ∠OT₁P = ∠OT₂P = 90°
∵ दोनों कोण OP व्यास वाले वृत्त के अन्दर अर्द्धवृत्त के कोण हैं।
∴ OT₁ ⊥ PT₁, OT₂ ⊥ PT₂
अत: रेखाएँ PT₁ व PT₂ अभीष्ट स्पर्शियाँ हैं।

प्रश्न 3. 3 cm त्रिज्या का एक वृत्त खींचिए। इसके किसी बढ़ाए गए व्यास पर केन्द्र से 7 cm की दूरी पर स्थित दो बिन्दु P और Q लीजिए। इन दोनों बिन्दुओं से वृत्त पर स्पर्श रेखाएँ खींचिए।
हल: दिया है : एक वृत्त जिसका केन्द्र 0 है तथा त्रिज्या 3 cm है। AOB वृत्त का एक व्यास है जिसको इस प्रकार बिन्दुओं P व Q तक बढ़ाया गया है कि वृत्त के केन्द्र O से प्रत्येक बिन्दु P व Q की दूरियाँ OP व OQ = 7 cm हैं।
रचना करनी है : बिन्दुओं P व Q से वृत्त की स्पर्श रेखाओं की।
रचना विधि :
1. O केन्द्र वाला 3 cm त्रिज्या का एक वृत्त खींचा।
2. इसका व्यास AOB खींचा और इसे दोनों ओर क्रमश: P व Q तक इस प्रकार बढ़ाया कि OP = OQ = 7 cm
3. OP व OQ के मध्य बिन्दु क्रमश: M₁ व M₂ ज्ञात किए।
4. केन्द्र M₁ से M₁O त्रिज्या का एक वृत्त खींचा जो O केन्द्र वाले वृत्त को बिन्दुओं T₁ व T₂ पर काटता है।
5. रेखाखण्ड PT₁ व PT₂ खींचे।
6. केन्द्र M₂ से M₂O त्रिज्या का एक वृत्त खींचा जो O केन्द्र वाले वृत्त को बिन्दुओं S₁ व S₂ पर काटता है।
7. रेखाखण्ड QS₁ तथा QS₂ खींचे।

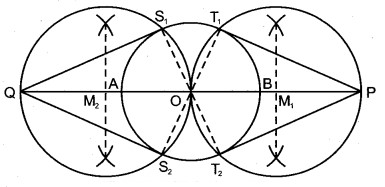
रेखाखण्ड PT₁, PT₂, QS₁ व QS₂ अभीष्ट स्पर्श रेखाएँ हैं।
उपपत्ति : केन्द्र O वाले वृत्त की त्रिज्याएँ OT₁, OT₂, OS₁ व OS₂ खींची।
∵ केन्द्र M वाले वृत्त में ∠OT₁P व ∠OT₂P अर्द्धवृत्तों में स्थित कोण हैं।
∴ ∠OT₁P व ∠OT₂P समकोण हैं जो क्रमशः त्रिज्याओं OT₁ व OT₂ के सिरों T₁ व T₂ पर स्थित हैं।
∴ PT₁ व PT₂ केन्द्र O वाले वृत्त की स्पर्श रेखाएँ हैं।
इसी प्रकार, QS₁ व QS₂ भी केन्द्र O वाले वृत्त की स्पर्शरेखाएँ हैं।

प्रश्न 4. 5 cm त्रिज्या के एक वृत्त पर ऐसी दो स्पर्श रेखाएँ खींचिए, जो परस्पर 60° के कोण पर झकी हों।
हल: दिया है : एक वृत्त जिसका केन्द्र O है तथा त्रिज्या 5 cm है।
रचना करनी है : वृत्त की दो स्पर्श रेखाओं की जिनके बीच का कोण 60° हो।
विश्लेषण : माना वृत्त का केन्द्र O तथा PT और BT इसकी दो स्पर्श रेखाएँ हैं जिनके बीच का कोण 60° है।
∵ ∠PTB = 60°
∴ ∠POB = 180° – 60° = 120°
⇒ ∠POA = 60°

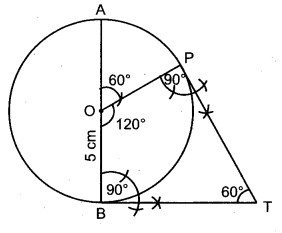
रचना विधि :
1. बिन्दु O को केन्द्र मानकर 5 cm त्रिज्या का एक वृत्त खींचा।
2. वृत्त का एक व्यास AB खींचा।
3. बिन्दु O पर OA से 60° का कोण बनाती हुई एक रेखा OP खींची जो वृत्त को बिन्दु P पर काटती है।
4. बिन्दु B पर OB के लम्बवत् एक रेखा खींची तथा बिन्दु P पर OP के लम्बवत् एक रेखा खींची। दोनों रेखाएँ एक-दूसरे को बिन्दु T पर काटती हैं।
अत: PT और BT वृत्त की दो अभीष्ट स्पर्श रेखाएँ हैं जो एक-दूसरे के साथ 60° का कोण बनाती हैं।
औचित्य : उपर्युक्त विश्लेषण ही अभीष्ट औचित्य है।

प्रश्न 5. 8 cm लम्बा एक रेखाखण्ड AB खींचिए। A को केन्द्र मानकर 4 cm त्रिज्या का एक वृत्त तथा B को केन्द्र मानकर 3 cm त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से स्पर्श रेखाओं की रचना कीजिए।
हल: दिया है : रेखाखण्ड AB = 8.0 cm। केन्द्र A से 4 cm त्रिज्या का एक वृत्त खींचा गया है तथा केन्द्र B से 3 cm त्रिज्या का एक अन्य वृत्त खींचा गया है।
रचना करनी है : केन्द्र बिन्दु A से केन्द्र B वाले वृत्त की दो स्पर्श रेखाओं तथा बिन्दु B से केन्द्र A वाले वृत्त की दो स्पर्श रेखाओं की।

रचना विधि:
1. रेखाखण्ड AB= 8 cm खींचा।
2. केन्द्र A से 4 cm त्रिज्या का एक वृत्त खींचा और केन्द्र B से 3 cm त्रिज्या का एक वृत्त खींचा।
3. AB का मध्य बिन्दु M ज्ञात किया।
4. M को केन्द्र मानकर AB व्यास का एक वृत्त खींचा जो A केन्द्र वाले वृत्त को बिन्दुओं S₁ व S₂ पर तथा B केन्द्र वाले वृत्त को बिन्दुओं T₁ व T₂ पर काटता है।
5. रेखाखण्ड S₁B व S₂B तथा AT₁ व AT₂ खींचे।
S₁B व S₂B केन्द्र A वाले वृत्त की तथा AT₁ व AT₂ केन्द्र B वाले वृत्त की स्पर्श रेखाएँ हैं।
उपपत्ति : ∵ केन्द्र M वाले वृत्त का AB व्यास है।
∴ ∠AS₁B, ∠AS₂B, ∠AT₁B व ∠AT₂B अर्द्धवृत्त के कोण हैं। अत: प्रत्येक समकोण है।
रेखाखण्ड AS₁ व AS₂ केन्द्र A वाले वृत्त और BT₁ व BT₂ केन्द्र B वाले वृत्त की त्रिज्याएँ हैं।
∴ S₁B व S₂B केन्द्र A वाले वृत्त और AT₁ व AT₂ केन्द्र B वाले वृत्त की स्पर्श रेखाएँ हैं।

प्रश्न 6. ABC एक समकोण त्रिभुज है, जिसमें AB = 6 cm, BC = 8 cm तथा ∠B = 90° है। B से AC पर BD लम्ब है। बिन्दुओं B, C व D से होकर जाने वाला एक वृत्त खींचा गया है। A से इस वृत्त पर स्पर्श रेखा की रचना कीजिए।
हल: दिया है : एक समकोण त्रिभुज ABC में AB = 6 cm, BC = 8 cm तथा ∠B = 90°| B से भुजा AC पर BD लम्ब खींचा गया है।
रचना करनी है : एक ऐसे वृत्त की जो बिन्दुओं B, C तथा D से होकर जाता है और बिन्दु A से इस वृत्त की स्पर्श रेखा की।
रचना विधि :
1. सर्वप्रथम दिए गए समकोण त्रिभुज ABC की रचना की।
2. बिन्दु B से AC पर लम्ब खींचा जो AC को D पर मिलता है।
3. ∆BCD की भुजाओं BD तथा CD के लम्ब समद्विभाजक खींचे जो परस्पर बिन्दुओं O पर काटते हैं।

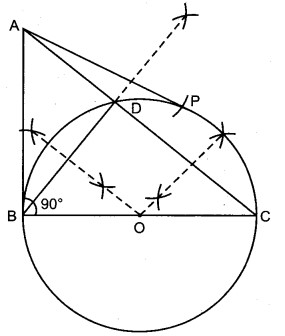
4. O को केन्द्र मानकर OB त्रिज्या से एक वृत्त खींचा जो बिन्दुओं B, C व D से होकर जाएगा।
5. AB स्वयं स्पर्श रेखा है; अत: A को केन्द्र BP मानकर AB त्रिज्या से चाप खींचे जो वृत्त को बिन्दु P पर काटते हैं।
AP अभीष्ट स्पर्श रेखा है।
औचित्य : ∠ABC = 90°, अत: रेखा AB स्वयं स्पर्श रेखा है।
AP = AB अतः रेखा AB, बिन्दु A से खींची गई दूसरी स्पर्श-रेखा है।

प्रश्न 7. किसी चूड़ी की सहायता से एक वृत्त खींचिए। वृत्त के बाहर एक बिन्दु लीजिए। इस बिन्दु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए।
हल: दिया है : एक वृत्त जिसका केन्द्र ज्ञात नहीं है। वृत्त के बाहर एक बिन्दु P है।

रचना करनी है : बिन्दु P से वृत्त की स्पर्श रेखाओं की।
रचना विधि :
1. बिन्दु P से ABP तथा CDP दो छेदक रेखाएँ खींची।
2. जीवाओं AB व CD के लम्ब समद्विभाजक खींचे जो परस्पर बिन्दु O पर काटते हैं। बिन्दु O दिए गए वृत्त का केन्द्र होगा।
3. रेखाखण्ड OP खींचा और इसका मध्य बिन्दु M ज्ञात किया।
4. M को केन्द्र मानकर MO त्रिज्या (OP व्यास) का वृत्त खींचा जो दिए गए वृत्त को क्रमश: बिन्दुओं T₁ व T₂ पर काटता है।
5. रेखाखण्ड PT₁ व PT₂ खींचे।
रेखाखण्ड PT₁ व PT₂ अभीष्ट स्पर्श रेखाएँ हैं।
औचित्य : केन्द्र O के बिन्दुओं T₁ व T₂ से मिलाया।
∠OT₁P = ∠OT₂P = 90° (अर्द्धवृत्त के कोण हैं)
∴ रेखाएँ PT₁ व PT₂ अभीष्ट स्पर्शियाँ हैं।

रचनाएँ Additional Questions

बहुविकल्पीय प्रश्न

प्रश्न 1.
एक रेखाखण्ड AB को p : q के अनुपात में विभाजित करने के लिए (यहाँ p और q धनात्मक पूर्णांक हैं), एक किरण AX खींचिए ताकि ∠BAX एक न्यून कोण हो। फिर किरण AX पर समान दूरियों पर इतने बिन्दु अंकित कीजिए कि इन बिन्दुओं की न्यूनतम संख्या हो।
(i) p और q में से बड़ी
(ii) p + q
(iii) p + q – 1
(iv) pq
हल
(ii) p + q

प्रश्न 2.
किसी वृत्त पर स्पर्श रेखाओं का ऐसा युग्म खींचने के लिए कि उनके बीच का कोण 35° हो, उन दो त्रिज्याओं के सिरों पर स्पर्श रेखाएँ खींचनी चाहिए, जिनके बीच का कोण हो
(i) 105°
(ii) 70°
(iii) 140°
(iv) 145°
हल
(iv) 145°

प्रश्न 3.
एक रेखाखण्ड AB को 5 : 7 के अनुपात में विभाजित करने के लिए, पहले एक किरण AX खींचिए, ताकि ∠BAX एक न्यून कोण हो और फिर किरण AX पर समान दूरियों पर बिन्दु अंकित किये जाएँ ताकि इनकी न्यूनतम संख्या हो
(i) 8
(ii) 10
(iii) 11
(iv) 12
हल
(iv) 12

प्रश्न 4.
एक रेखाखण्ड AB को 4 : 7 के अनुपात में विभाजित करने के लिए, पहले एक किरण AX इस प्रकार खींची जाती है कि ∠BAX एक न्यूनकोण हो और फिर किरण AX पर समान दूरियों पर बिन्दु, A₁, A₂, A₃,…. अंकित किए जाते हैं और बिन्दु B को निम्नलिखित से मिलाया जाता है
(i) A₁₂
(ii) A₁₁
(iii) A₁₀
(iv) A₉
हल
(ii) A₁₁

प्रश्न 5.
एक रेखाखण्ड AB को 5 : 6 के अनुपात में विभाजित करने के लिए, एक किरण AX खींचिए ताकि ∠BAX एक न्यूनकोण हो, फिर BY किरण AX के समांतर विपरीत दिशा में खींचिए। इसके बाद AX और BY किरणों पर क्रमशः समान दूरियों पर बिन्दु A₁, A₂, A₃, …और B₁, B₂, B₃,… अंकित किए जाएँ। फिर जिन बिन्दुओं को मिलाया जाता है वे हैं
(i) A₅ और B₆
(ii) A₆ और B₅
(iii) A₄ और B₅
(iv) A₅ और B₄
हल
(i) A₅ और B₆

प्रश्न 6.
किसी वृत्त पर स्पर्श रेखाओं का एक ऐसा युग्म खींचने के लिए कि उनके बीच कोण 60° हों, उन दो त्रिज्याओं के सिरों पर स्पर्श रेखाएँ खींचनी चाहिए जिनके बीच का कोण हो
(i) 135°
(ii) 90°
(iii) 60°
(iv) 120°
हल
(iv) 120°

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
3.0 cm त्रिज्या के वृत्त के किसी बिन्दु P पर स्पर्श रेखा खींचिए।
या
6.0 cm व्यास के एक वृत्त की रचना कीजिए और वृत्त के किसी बिन्दु पर स्पर्शरेखा खींचिए और रचना-विधि लिखिए।
हल
दिया है : एक वृत्त जिसका केन्द्र O तथा व्यास 6.0 cm है।
रचना करनी है : वृत्त के बिन्दु P पर वृत्त की स्पर्शरेखा की

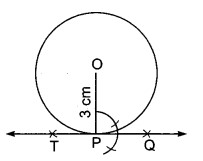
रचना विधि :
1. सर्वप्रथम O को केन्द्र मानकर 6.0/2 = 3.0 cm त्रिज्या का वृत्त खींचा और वृत्त पर कोई बिन्दु P लिया।
2. O को P से मिलाया।
3. बिन्दु P पर PQ ⊥ OP खींचा।
AB वृत्त के बिन्दु A पर अभीष्ट स्पर्श रेखा है। यही रचना करनी थी।

प्रश्न 2.
ऐसे वृत्त की रचना कीजिए, जिसकी त्रिज्या 3.5 cm तथा जो 5 cm दूरी पर स्थित बिन्दुओं A और B से होकर जाता है।
हल
दिया है : 5 cm दूर स्थित दो बिन्दु A और B हैं।
रचना करनी है : 3.5 cm त्रिज्या के वृत्त की जो A और B बिन्दुओं से होकर जाता है।

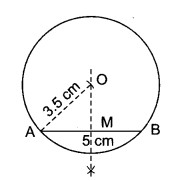
रचना विधि :
1. AB का लम्ब समद्विभाजक OM खींचा जो AB को बिन्दु M पर काटता है।
2. A को केन्द्र मानकर तथा 3.5 cm त्रिज्या लेकर एक चाप खींचा जो OM को बिन्दु O पर काटता है।
3. O को केन्द्र मानकर तथा 3.5 cm त्रिज्या लेकर एक वृत्त खींचा जो A और B से होकर जाता है।
यही रचना करनी थी।

लघु उत्तरीय प्रश्न

प्रश्न 1.
चित्र में AB, AC और PQ वृत्त O की स्पर्श रेखाएँ हैं। यदि AB = 5 cm, ∆APQ का परिमाप ज्ञात कीजिए।
हल
किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्शियाँ लम्बाई में बराबर होती हैं।

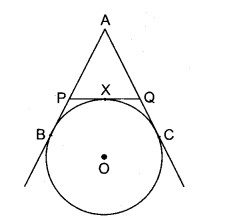
AB = AC = 5 cm
इसी प्रकार, PB = PX, QC = QX
त्रिभुज का परिमाप = AP + PQ + QA
= AP + PX + XQ + AQ
= AP + PB + QC + QA
= AB + AC
= 5 + 5
= 10 cm

प्रश्न 2.
संलग्न चित्र में AQ, AR तथा BC वृत्त के क्रमशः Q, R तथा P बिन्दुओं पर खींची गई स्पर्शियाँ हैं यदि AR = 8 cm है तो ∆ABC का परिमाप ज्ञात कीजिए। हल

किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्शियाँ लम्बाई में बराबर होती हैं।
अतः AQ = AR = 8 cm
इसी प्रकार, CP = CR तथा BP = BQ
त्रिभुज का परिमाप = AB + BC + CA
= AB + (BP + PC) + CA
= AB + BQ + CR + AC
= AQ + AR
= 8 + 8
= 16 cm

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
3 cm त्रिज्या का एक वृत्त खींचिए। वृत्त के केन्द्र से 5 cm दूर स्थित एक बिन्दु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और उनकी लम्बाई मापिए।
हल
रचना विधि :
1. सर्वप्रथम 5 cm लम्बाई का रेखाखण्ड OP खींचा।
2. बिन्दु O को केन्द्र मानकर 3 cm त्रिज्या का वृत्त खींचा।
3. OP का लम्बार्धक खींचा जो इसे बिन्दु M पर काटता है।
4. बिन्दु M को केन्द्र मानकर OM त्रिज्या का एक वृत्त खींचा जो केन्द्र O के दिए हुए वृत्त को A और B बिन्दुओं पर काटता है।
5. PA तथा PB को मिलाया जो वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।

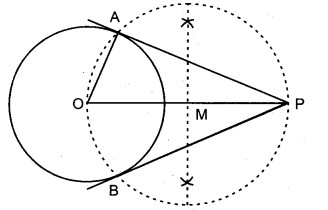
उपपत्ति : रेखाखण्ड OA खींचा।
∵ M, OP का मध्य-बिन्दु है जिससे OP व्यास है।
तब, वृत्त OAPB में, ∠OAP, अर्द्धवृत्त OAPO में स्थित है।
∴ ∠OAP = 90°
और OA त्रिज्या है।
तब, AP, त्रिज्या OA पर लम्ब है।
∴ AP वृत्त की स्पर्श रेखा है। इसी प्रकार BP भी वृत्त की स्पर्श रेखा है।
माप करने पर प्रत्येक स्पर्श रेखा की लम्बाई = 4 cm

प्रश्न 2.
एक दिए गए त्रिभुज ABC के समरूप एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए गए त्रिभुज ABC की संगत भुजाओं की 3/4 हों।
हल
दिया है : एक त्रिभुज ABC
रचना करनी है : एक अन्य त्रिभुज की जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की 3/4 हों।

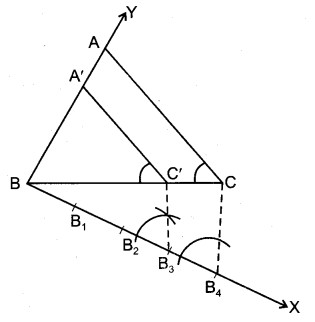
रचना विधि :
1. BC के बिन्दु B से ∠CBX चित्र की भाँति नीचे की ओर बनाया।
2. BX में से चार समान भाग BB₁, B₁B₂, B₂B₃ और B₃B₄ काटे।
3. B₄C खींची और B₃ से B₄C के समान्तर एक रेखा खींची जो BC से C’ पर मिलती है।
4. C’ से AC के समान्तर रेखा C’A’ खींची जो AB से A’ पर मिलती है।
∆ABC’ अभीष्ट त्रिभुज है।

प्रश्न 3.
5 cm, भुजा वाले एक समबाहु त्रिभुज ABC की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 6/7 गुनी हों।
हल
दिया है : समबाहु ∆ABC में भुजा AB = BC = CA = 5 cm
रचना करनी है : एक समबाहु ∆ABC की तथा इसके समरूप एक ∆ की प्रत्येक भुजा ∆ABC की संगत भुजा की 6/7 गुनी हो।

रचना विधि :
1. रेखाखण्ड BC = 5 cm खींचा।
2. B और C को केन्द्र मान कर 5 सेमी के दो चाप लगाए जो एक-दूसरे को A पर काटते हैं।
3. AB और AC को मिलाया। ABC अभीष्ट समबाहु ∆ है।
4. B से न्यूनकोण बनाती हुई रेखा BX खींची। उसमें से BB₁, B₁B₂, B₂B₃, B₃B₄, B₄B₅, B₅B₆ व B₆B₇ के 7 समान भाग काटे।
5. ऋजु रेखा CB₇ खींची।
6. B₆ से CB₇ के समान्तर ऋजु रेखा C’B₆ खींची।
7. C’ से CA के समान्तर ऋजु रेखा C’A’ खींची जो AB को A’ पर मिलती है जिससे A’B = 6/7 AB, ∆A’BC’ अभीष्ट समरूप त्रिभुज है।

प्रश्न 4.
एक समद्विबाहु त्रिभुज ABC की रचना कीजिए, जिसकी भुजाएँ AB = AC = 4.6 cm और ऊँचाई 3.6 cm। फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी संगत भुजाएँ त्रिभुज ABC की संगत भुजाओं के 3/2 गुनी है।
हल
दिया है : समद्विबाहु ∆ABC में AB = AC = 4.6 cm और ऊँचाई = 3.6 cm
रचना करनी है : उक्त समद्विबाहु त्रिभुज की और एक अन्य त्रिभुज की जिसकी भुजाएँ दिए हुए समद्विबाहु त्रिभुज की संगत भुजाओं की 3/2 हों।

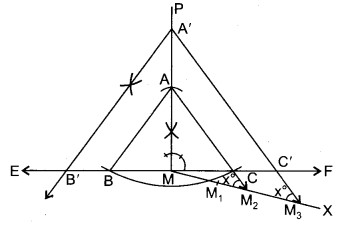
रचना विधि :
1. रेखा EF खींची।
2. इस पर कोई बिन्दु M लिया। इस पर एक लम्ब MP खींचा। इसमें से MA = 3.6 cm काटा।
3. A को केन्द्र मान कर 4.6 cm दूरी पर दो चाप लगाए जो EF को B और C में काटते हैं।
4. AB और AC को मिलाया। समद्विबाहु त्रिभुज ABC प्राप्त किया।
5. बिन्दु M पर BC से नीचे की ओर न्यूनकोण बनाती हुई रेखा MX खींची।
6. MX में से 3 समान भाग MM₁, M₁M₂, M₂M₃ खींचे।
7. रेखाखण्ड M₂C खींचा और M₃ से M₂C के समान्तर रेखा खींची जो EF को C’ पर मिलती है।
8. C’ से AC के समान्तर C’A’ खींची जो MP से A’ पर मिलती है।
9. अब A’ से AB के समान्तर A’B’ रेखा खींची जो EF से B’ पर मिलती है।
∆A’B’C’ अभीष्ट त्रिभुज है।

प्रश्न 5.
दो वृत्तों पर जिनकी त्रिज्याएँ 3.2 cm और 1.5 cm हैं और जिनके केन्द्रों के बीच की दूरी 6.2 cm है, उभयनिष्ठ अनुस्पर्श रेखाएँ खींचिए। इन स्पर्श रेखाओं की माप बताइए। गणना द्वारा उत्तर की जाँच कीजिए।
हल
दिया है : 3.2 cm तथा 1.5 cm त्रिज्या के O तथा E केन्द्रीय दो वृत्त जिनके केन्द्रों के बीच की दूरी OE = 6.2 cm है।
अभीष्ट :
(i) दोनों वृत्तों के उभयनिष्ठ अनुस्पर्शी रेखाओं की रचना करनी है।
(ii) उनकी लम्बाई नापकर लिखनी है।
(iii) गणना द्वारा उत्तर की जाँच करनी है।

रचना विधि :
1. सर्वप्रथम रेखाखण्ड OE = 6.2 cm खींचा।
2. O पर 3.2 cm त्रिज्या का वृत्त खींचा तथा E पर 1.5 cm त्रिज्या का वृत्त खींचा।
3. OE को व्यास मानकर एक वृत्त खींचा तथा O को केन्द्र मानकर 3.2 – 1.5 = 1.7 cm त्रिज्या का वृत्त खींचा जो OE व्यास वाले वृत्त को बिन्दुओं C और C’ पर काटता है।
4. OC और OC’ को मिला कर आगे बढ़ाया जो बड़े वृत्त को D तथा D’ बिन्दुओं पर काटती हैं।
5. OD और OD’ के समान्तर छोटे वृत्त के केन्द्र E से क्रमश: EB तथा EB रेखाएँ खींची जो वृत्त को बिन्दुओं B तथा B पर काटती हैं। DB और DB को मिलाया।
नापने पर इनकी लम्बाई 6 cm लगभग है।
यही रचना करनी थी।
गणना द्वारा पुष्टि : उभयनिष्ठ अनुस्पर्शी रेखा की लम्बाई

प्रश्न 6.
दो वृत्तों के केन्द्रों के बीच की दूरी 10 cm है, जिनकी त्रिज्या क्रमशः 4.5 cm व 3.5 cm हैं। वृत्तों की उभयनिष्ठ तिर्यक स्पर्शरेखा खींचिए तथा स्पर्शरेखा की लम्बाई नापकर लिखिए तथा गणना द्वारा उत्तर की जाँच कीजिए।
हल
दिया है : 3.5 cm तथा 4.5 cm त्रिज्या के O तथा E केन्द्रीय दो वृत्त जिनके केन्द्रों के बीच की दूरी OE = 10 cm
अभीष्ट :
(i) दोनों वृत्तों के उभयनिष्ठ तिर्यक स्पर्शरेखाओं की रचना करनी है।
(ii) स्पर्शरेखाओं की लम्बाई नापकर लिखनी है।
(iii) स्पर्शरेखा की लम्बाई गणना द्वारा जाँचनी है।

रचना विधि :
1. सर्वप्रथम रेखाखण्ड OE = 10 cm खींचा।
2. O को केन्द्र मानकर 3.5 cm त्रिज्या का वृत्त तथा E को केन्द्र मानकर 4.5 cm त्रिज्या का वृत्त खींचा।
3. O को केन्द्र मानकर 3.5 + 4.5 = 8 cm त्रिज्या का वृत्त खींचा और OE को व्यास मानकर वृत्त खींचा जो 8 cm त्रिज्या वाले वृत्त को D तथा D’ पर काटता है।
4. OD तथा OD’ को मिलाया जो 3.5 cm त्रिज्या वाले वृत्त को C तथा C’ पर काटती हैं।
5. E से OD के समान्तर EB तथा OD’ के समान्तर EB’ खींची जो E केन्द्र वाले वृत्त को B तथा B बिन्दुओं पर काटती हैं।
6. BC तथा B’C’ को मिलाया। ये ही उभयनिष्ठ तिर्यक स्पर्श रेखा हैं।
नापने पर इनकी लम्बाई 6 cm है।
यही रचना करनी थी।
गणना द्वारा पुष्टि : तिर्यक उभयनिष्ठ स्पर्शरेखा की लम्बाई

tense in english