bihar board class 10th maths | Circles (वृत्त)

Bihar Board Solutions for Class 10 Maths Chapter 10 Circles (वृत्त)

प्रश्नावली 10.1

प्रश्न 1. एक वृत्त की कितनी स्पर्श रेखाएँ हो सकती हैं?
हलः एक वृत्त की अनगिनत स्पर्श-रेखाएँ हो सकती हैं।

प्रश्न 2. रिक्त स्थानों की पूर्ति कीजिएः
(i) किसी वृत्त की स्पर्श रेखा उसे बिंदु ………….. पर प्रतिच्छेद करती है।
(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को …………. कहते हैं।
(iii) एक वृत्त की ………….. समांतर स्पर्श रेखाएँ हो सकती हैं।
(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को ………….. कहते हैं।
हलः
(i) केवल एक
(ii) छेदक-रेखा
(iii) दो।
(iv) स्पर्श बिन्दु

प्रश्न 3. 5 सेमी त्रिज्या वाले एक वृत्त के बिन्दु P पर स्पर्श रेखा PR केन्द्र O से जाने वाली एक रेखा से बिन्दु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी PQ की लम्बाई है-
(A) 12 सेमी
(B) 13 सेमी
(C) 8.5 सेमी
(D) √119 सेमी
हल:
दिया है, त्रिज्या OP = 5 सेमी है तथा OQ = 12 सेमी
हम जानते हैं कि वृत्त के किसी बिन्दु पर स्पर्श रेखा स्पर्श बिन्दु से जाने वाली त्रिज्या पर लम्ब होती है।

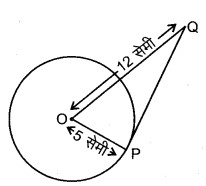
∴ OP ⊥ PQ
समकोण ∆OPQ में, पाइथागोरस प्रमेय से,
OP² + PQ² = OQ²
⇒ (5)² + PQ² = (12)²
⇒ PQ² = 12² – 5² = 144 – 25 = 119
⇒ PQ = √119 सेमी
अत: विकल्प (D) सही है।

प्रश्न 4. एक वृत्त खींचिए और एक दी गई रेखा के समान्तर दो ऐसी रेखाएँ खींचिए कि उनमें से एक स्पर्श रेखा हो तथा दूसरी छेदक रेखा हो।
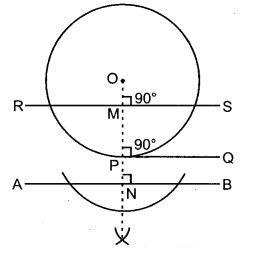
हल: एक वृत्त बनाया जिसका केन्द्र O है और माना AB एक दी गई रेखा है।
हमें AB के समान्तर दो रेखाएँ (माना PQ व RS) खींचनी हैं जिनमें PQ स्पर्श रेखा और RS छेदक रेखा हो।
रचना विधि :
(i) रेखा AB पर केन्द्र-बिन्दु से लम्ब ON खींचा जो वृत्त को बिन्दु P पर काटता है।
(ii) त्रिज्या OP के बिन्दु P पर लम्ब PQ खींचिए। PQ स्पर्श रेखा है।
(iii) OP पर एक बिन्दु M लेकर M से OP पर लम्ब RS खींचा। RS छेदक रेखा है।

प्रश्नावली 10.2

प्रश्न सं. 1,2,3 में सही विकल्प चुनिए एवं उचित कारण दीजिए।

प्रश्न 1. एक बिन्दु से एक वृत्त पर स्पर्श रेखा की लम्बाई 24 cm तथा Q की केन्द्र से दूरी 25 cm है। वृत्त की त्रिज्या है :
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
हल:

माना वृत्त की त्रिज्या R cm है।
दिया है, स्पर्श रेखा की लम्बाई (PQ) = 24 cm
और बिन्दु Q से वृत्त के केन्द्र की दूरी (OP) = 25 cm
समकोण ΔOPQ में, पाइथागोरस प्रमेय से,
OQ² = OP² + PQ²
⇒ OP² = OQ² – PQ²
⇒ R² = (25)² – (24)²
⇒ R² = 625 – 576
⇒ R² = 49
⇒ R = 7
अत: विकल्प (A) सही है।

प्रश्न 2. आकृति में, यदि TP, TQ केंद्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110°, तो ∠PTQ बराबर हैं:
(A) 60°
(B) 70°
(C) 80°
(D) 90°

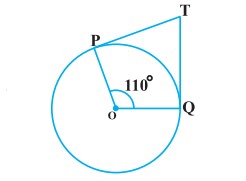
हलः आकृति में O वृत्त का केन्द्र है, बाह्य बिन्दु T से दो स्पर्श रेखाएँ TP और TQ इस प्रकार हैं कि
∠POQ = 110°
OP ⊥ PT और OQ ⊥ QT
⇒ ∠OPT = 90° और ∠OQT = 90°
अब, चतुर्भुज TPOQ में, हमें प्राप्त है:
∠PTQ + 90° + 110° + 90° = 360°
⇒ ∠PTQ + 290° = 360°
⇒ ∠PTQ = 360° – 290° = 70°
इस प्रकार विकल्प (B) सही है।

प्रश्न 3. यदि एक बिंदु P से O केंद्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हों, तो ∠POA बराबर हैः
(A) 50°
(B) 60°
(C) 70°
(D) 80°

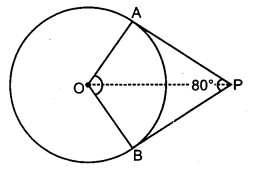
हलः चूंकि, वृत्त का केन्द्र O और P से वृत्त की दो स्पर्श रेखाएँ PA और PB हैं:
OA ⊥ AP और OB ⊥ BP
∠OAP = ∠OBP = 90°
अब, चतुर्भुज PAOB में, हमें प्राप्त है:
∠APB + ∠PAO + ∠AOB + ∠PBO = 360°
⇒ 80° + 90° + ∠AOB + 90° = 360°
⇒ 260° + ∠AOB = 360°
⇒ ∠AOB = 360° – 260°
⇒ ∠AOB = 100°
अब, समकोण ∆OAP तथा समकोण ∆OBP में,
OP = OP [उभयनिष्ठ]
∠OAP = ∠OBP [प्रत्येक = 90°]
OA = OB [एक ही वृत की त्रिज्याएँ]
∆OAP = ∆OBP [SAS]
इनके संगत-अंग समान होंगे।
∠POA = ∠POB
⇒ ∠POA = ∠AOB = x 100° = 50°
इस प्रकार, विकल्प (A) सही है।

प्रश्न 4. सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं।
हल:

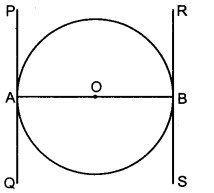
दिया है : एक वृत्त का केन्द्र O तथा व्यास AB है। व्यास के सिरों A तथा B से वृत्त पर स्पर्श रेखाएँ PAQ तथा RBS खींची गई हैं।
सिद्ध करना है : PQ || RS
उपपत्ति : दिया है, AB वृत्त का व्यास है और PAQ तथा RBS बिन्दुओं A तथा B पर वृत्त की स्पर्श रेखाएँ हैं।
∴ ∠PAB = 90° तथा ∠ABS = 90°
परन्तु ∠PAB तथा ∠ABS ऋजु रेखाओं PQ तथा RS को तिर्यक रेखा AB के द्वारा काटने से बने समान एकान्तर कोण हैं।
PQ || RS

प्रश्न 5. सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
हल:

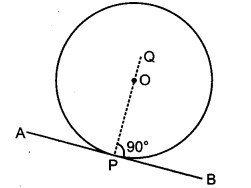
दिया है : एक वृत्त का केन्द्र O है और AB वृत्त की स्पर्श रेखा है जो वृत्त को बिन्दु P पर स्पर्श करती है।
P से वृत्त की स्पर्श रेखा AB पर PQ लम्ब खींचा गया है।
सिद्ध करना है : लम्ब PQ वृत्त के केन्द्र O से जाता है।
उपपत्ति: ∵ AP,वृत्त के स्पर्श बिन्दु P पर स्पर्श-रेखा है।
∴ AP, वृत्त की त्रिज्या पर लम्ब होगी।
∵ PQ ⊥ AP
∴ PQ रेखा में वृत्त की त्रिज्या समाहित होगी।
∵ त्रिज्या का एक सिरा P है, तब दूसरा सिरा केन्द्र O होगा।
∴ रेखा PQ में केन्द्र O भी समाहित है।
अतः लम्ब PQ वृत्त के केन्द्र O से होकर जाता है।

प्रश्न 6. एक बिन्दु A से, जो एक वृत्त के केन्द्र से 5 cm दूरी पर है, वृत्त पर स्पर्श रेखा की लम्बाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल:
बिन्दु A से वृत्त के केन्द्र की दूरी (D) = 5 cm
और वृत्त की स्पर्श रेखा की लम्बाई (T) = 4 cm
माना वृत्त की त्रिज्या R cm है।
∵ बिन्दु A से,
(वृत्त की स्पर्श रेखा की लम्बाई)² = (वृत्त के केन्द्र से दूरी)² – (त्रिज्या)²
⇒ T² = D² – R²
⇒ (4)² = (5)² – R²
⇒ R² = 5² – 4² = 25 – 16 = 9
⇒ R = 3 cm
अत: वृत्त की त्रिज्या (R) = 3 cm

प्रश्न 7. दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
हल:

माना O केन्द्र वाले दो संकेन्द्रीय वृत्त हैं जिनकी त्रिज्याएँ OA तथा OP क्रमश: 5 cm व 3 cm हैं।
बड़े वृत्त की एक जीवा AB है जो छोटे वृत्त को बिन्दु P पर स्पर्श करती है।
∴ OP ⊥ AB (OP वृत्त की त्रिज्या है)
∴ ∆OAP समकोणीय त्रिभुज है।
तब, पाइथागोरस प्रमेय से,
AP² + OP² = OA²
⇒ AP² + (3)² = (5)²
⇒ AP² = (5)² – (3)² = 25 – 9 = 16
⇒ AP = 4 cm
परन्तु बड़े वृत्त में, जीवा AB पर केन्द्र O से OP लम्ब है।
∴ P, AB को अर्धित करता है
∴ AP = BP
⇒ BP = 4 cm
तब, जीवा AB की लम्बाई = AP + BP = 4 + 4 = 8 cm

प्रश्न 8. एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है। सिद्ध कीजिए-
AB + CD = AD + BC

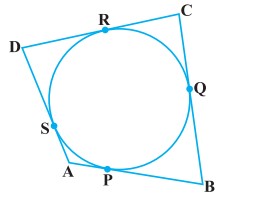
हल:
दिया है : O केन्द्र वाले वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है जिसकी भुजाएँ AB, BC, CD तथा DA वृत्त को क्रमशः बिन्दुओं P, Q, R और S पर स्पर्श करती हैं।
सिद्ध करना है : AB + CD = AD + BC
उपपत्ति: ∴ AB तथा AD वृत्त को P तथा S पर स्पर्श करती हैं।
AP= AS
पुन: AB तथा BC वृत्त को P तथा Q पर स्पर्श करती हैं।
∴ PB = BQ
∵ BC तथा CD वृत्त को Q तथा R पर स्पर्श करती हैं।
∴ QC = CR
और CD तथा DA वृत्त को R तथा S पर स्पर्श करती हैं।
∴ DR = SD
AB + CD = AP + PB + DR + CR (आकृति देखिए)
= AS + BQ + SD + QC
= (AS + SD) + (BQ + QC)
= AD + BC
अत: AB + CD = AD + BC

प्रश्न 9. संलग्न आकृति में, XY और X’Y’, O केन्द्र के वाले एक वृत्त की दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A पर तथा X’Y’ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ∠AOB = 90° है।

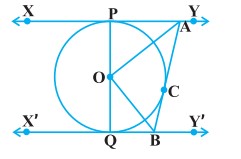
हल: दिया है : O केन्द्र वाले वृत्त की XY तथा X’Y’ दो समान्तर स्पर्श रेखाएँ हैं। वृत्त पर एक बिन्दु C से स्पर्श रेखा AB खींची गई है जो XY को A पर तथा X’Y’ को B पर काटती है। OA तथा OB को मिलाया गया है।

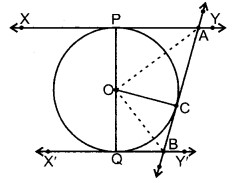
सिद्ध करना है : ∠AOB = 90°
रचना : रेखाखण्ड OC खींचा।
उपपत्ति : ∵ XY और X’Y’ वृत्त की दो समान्तर स्पर्श रेखाएँ हैं जो वृत्त को (माना) P तथा Q पर स्पर्श करती हैं। C से वृत्त की एक स्पर्श रेखा AB, XY को A पर तथा X’Y’ को B पर काटती है।
∴ बिन्दु A से वृत्त पर AP व AC स्पर्श रेखाएँ हैं।
तब, ∆OPA व ∆OCA में,
OP = OC (वृत्त की त्रिज्याएँ हैं)
AP = AC (बाह्य बिन्दु से वृत्त की स्पर्श रेखाएँ हैं)
OA = OA (उभयनिष्ठ भुजा है)
∆OPA ≅ ∆OCA
∠POA = ∠AOC …….(1)
इसी प्रकार, बिन्दु B से वृत्त पर BQ और BC स्पर्श रेखाएँ हैं।
तब, ∆OQB तथा ∆OBC में,
OQ = OC (वृत्त की त्रिज्याएँ हैं)
BQ = BC (बिन्दु B से वृत्त की स्पर्श रेखाएँ हैं)
OB = OB (उभयनिष्ठ भुजा है)
∆OQB ≅ ∆OBC
∠BOQ = ∠COB …….(2)
∵ ∠POA + ∠AOC + ∠COB + ∠BOQ = 180°
⇒ ∠AOC + ∠AOC + ∠COB + ∠COB = 180° [समीकरण (1) व समीकरण (2) से]
⇒ 2(∠AOC + ∠COB) = 180°
⇒ ∠AOC + ∠COB = 90°
अतः ∠AOB = 90°

प्रश्न 10. सिद्ध कीजिए कि किसी बाह्य बिन्दु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक होता है।
हल:

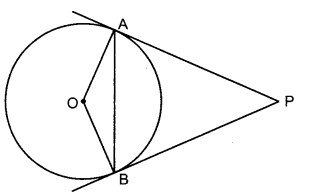
दिया है : O केन्द्र वाले वृत्त के बाहर एक बिन्दु P है। Pसे वृत्त पर PA तथा PB दो स्पर्श रेखाएँ खींची गई हैं। स्पर्श रेखाओं के बीच का ∠APB है। स्पर्श बिन्दुओं को रेखा AB मिलाती है जो वृत्त के केन्द्र पर ∠AOB बनाती है।
सिद्ध करना है : ∠APB, ∠AOB का सम्पूरक है।
उपपत्ति: ∵ OA वृत्त की त्रिज्या है और बाह्य बिन्दु P से PA स्पर्श रेखा है जो वृत्त को बिन्दु A पर स्पर्श करती है।
∴ ∠OAP = 90° …….(1)
इसी प्रकार, OB वृत्त की त्रिज्या है और बाह्य बिन्दु P से PB वृत्त की स्पर्श रेखा है जो वृत्त को बिन्दु B पर स्पर्श करती है।
∴ ∠OBP = 90° …….(2)
समीकरण (1) व (2) को जोड़ने पर,
∠OAP + ∠OBP = 180°
तब, चतुर्भुज OAPB में,
∠AOB + ∠OAP + ∠OBP + ∠APB = 360°
⇒ ∠AOB + 180° + ∠APB = 360°
⇒ ∠AOB + ∠APB = 360° – 180° = 180°
⇒ ∠AOB + ∠APB = 180°
अत: ∠APB, ∠AOB का सम्पूरक है।

प्रश्न 11. सिद्ध कीजिए कि किसी वृत्त के परिगत समान्तर चतुर्भुज, समचतुर्भुज होता है।
हल:

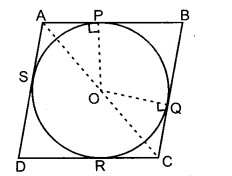
दिया है : केन्द्र O वाले वृत्त के परिगत खींचा गया समान्तर चतुर्भुज ABCD जिसकी भुजाएँ वृत्त को क्रमशः P, Q, R और S बिन्दुओं पर स्पर्श करती हैं।
सिद्ध करना है : ABCD एक समचतुर्भुज है।
रचना : AC, OP और OQ को मिलाया।
उपपत्ति : चूँकि बाह्य बिन्दु से वृत्त पर खींची गई दोनों स्पर्श रेखाएँ लम्बाई में बराबर होती हैं,
∴ AP = AS, BP = BQ, CQ = CR तथा DR = DS
अब, ∆OAP और ∆OCQ में,
OP = OQ (एक ही वृत्त की त्रिज्याएँ हैं)
∠OAP = ∠OCQ (समान्तर चतुर्भुज के सम्मुख कोणों के अर्द्धक हैं)
∠OPA = ∠OQC (प्रत्येक समकोण है)
दोनों त्रिभुज सर्वांगसम हैं अर्थात् ∆OAP ≅ ∆OCQ
⇒ AP = CQ
⇒ AP + BP = CQ + BQ (∵ BP = BQ)
⇒ AB = BC
इसी प्रकार सिद्ध कर सकते हैं कि AD = AB तथा BC = CD
∴ समान्तर चतुर्भुज ABCD में,
AB = CD = BC = AD
अत: ABCD एक समचतुर्भुज है।

प्रश्न 12. 4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिन्दु Dद्वारा BC विभाजित है) की लम्बाइयाँ क्रमशः 8 cm और 6 cm हैं। भुजाएँ AB और AC ज्ञात कीजिए।

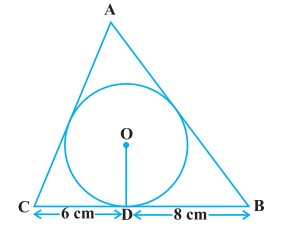
हल: चित्र में, ABC एक त्रिभुज है जिसके अन्तर्वृत्त का केन्द्र O है तथा अन्तर्वृत्त की त्रिज्याएँ OD = OE = OF = 4 cm हैं।
स्पर्श बिन्दु D से BC के खण्ड BD = 6 cm तथा DC = 8 cm हैं।

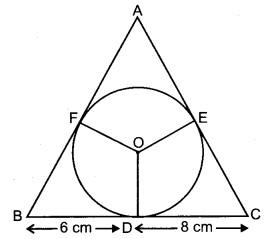
तब, BF = 6 cm तथा CE = 8 cm
माना AF = AE = x cm
तब, AB = AF + BF = (x + 6) cm
⇒ c = (x + 6) cm [∵ ∆ABC से BC = a, AB = c, CA = b]
BC = 8 + 6 = 14 cm
⇒ a = 14 cm
तथा CA = AE + CE = (x + 8) cm
⇒ b = (x + 8) cm

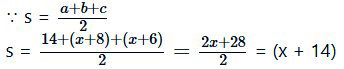
(s – a) = (x + 14) – 14 = x
(s – b) = (x + 14) – (x + 8) = 6
(s – c) = (x + 14) – (x + 6) = 8

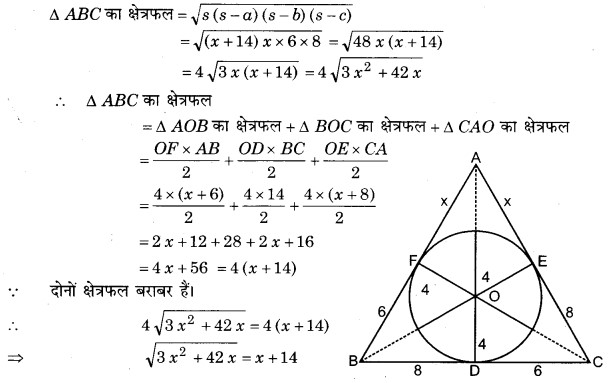
दोनों पक्षों का वर्ग करने पर,
3x² + 42x = (x + 14)²
⇒ 3x² + 42x = x² + 28x + 196
⇒ 3x² + 42x – x² – 28x – 196 = 0
⇒ 2x² + 14x – 196 = 0
⇒ x² + 7x – 98 = 0
⇒ x² + (14 – 7)x – 98 = 0
⇒ x² + 14x – 7x – 98 = 0
⇒ (x² + 14x) – (7x + 98) = 0
⇒ x(x + 14) – 7(x + 14) = 0
⇒ (x + 14) (x – 7) = 0
यदि x + 14 = 0, तो x = -14
और यदि x – 7 = 0, तो x = 7
x का मान -14 ऋणात्मक है जो लम्बाई नहीं हो सकता। अत: यह स्वीकार्य नहीं है।
तब, x = 7
∴ भुजा AB = x + 6 = 7 + 6 = 13 cm
तथा भुजा CA = x + 8 = 7 + 8 = 15 cm
अत: त्रिभुज की अन्य दो भुजाएँ AB व CA क्रमश: 13 cm व 15 cm हैं।

प्रश्न 13. सिद्धं कीजिए कि वृत्त के परिगत बने चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
हल:

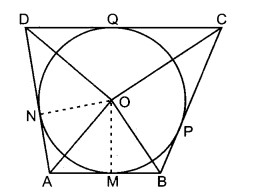
दिया है : केन्द्र O वाले वृत्त के परिगत चतुर्भुज ABCD खींचा गया है जिसकी भुजाएँ AB, BC, CD व DA वृत्त को क्रमशः बिन्दुओं M, P, Q व N पर स्पर्श करती हैं।
सिद्ध करना है : ∠AOB + ∠COD = 180°
रचना : स्पर्श बिन्दु M और N को केन्द्र O से मिलाया।
उपपत्ति : माना ∠A = 2α, ∠B = 2β, ∠C = 2γ, ∠D = 2δ
∆OAM और ∆OAN में,
∠OMA = ∠ONA (प्रत्येक समकोण है)
OM = ON (एक ही वृत्त की त्रिज्या है)
OA = OA
∴ दोनों त्रिभुज सर्वांगसम हैं अर्थात् ∆OAM ≅ ∆OAN
⇒ ∠OAM = ∠OAN = 1/2 (∠A) = 1/2 (2α) = α
⇒ ∠OAB = ∠OAD = α
इसी प्रकार, ∠OBA = ∠OBC = β
∠OCB = ∠OCD = γ
तथा ∠ODA = ∠ODC = δ
अब, ∆AOB में,
∠AOB = 180° – ∠OAB – ∠OBA = 180° – α – β = 180° – (α + β)
तथा ∠COD = 180° – ∠OCD – ∠ODC = 180° – γ – δ = 180° – (γ + δ)
समीकरण (1) व (2) को जोड़ने पर,
∠AOB + ∠COD = {180° – (α + β)} + {180° – (γ + δ)}
⇒ ∠AOB + ∠COD = 360° – (α + β + γ + δ)
परन्तु ∠A + ∠B + ∠C + ∠D = 360°
⇒ 2α + 2β + 2γ + 2δ = 360°
⇒ α + β + γ + δ = 180°
अत: समीकरण (3) से,
∠AOB + ∠COD = 360° – 180° = 180°

वृत्त Additional Questions

बहुविकल्पीय प्रश्न

प्रश्न 1.
चित्र में O केन्द्र वाले वृत्त की त्रिज्या OD = 4 cm है। यदि OB = 5 cm हो, तो स्पर्श रेखा BC की लम्बाई होगी
(i) 3 cm
(ii) 4 cm
(iii) 2 cm
(iv) 3.5 cm
हल
(i) 3 cm

प्रश्न 2.
दो वृत्त परस्पर बाह्य स्पर्श करते हैं। उनकी त्रिज्याएँ 3.6 cm और 1.6 cm हैं। इनके केन्द्रों के बीच की दूरी होगी
(i) 1.6 cm
(ii) 3.6 cm
(iii) 2.0 cm
(iv) 5.2 cm
हल
(iv) 5.2 cm

प्रश्न 3.
दो वृत्त एक-दूसरे को बाह्यतः स्पर्श करते हैं। उनके केन्द्रों के बीच की दूरी 7 cm और एक वृत्त की त्रिज्या 3 cm है, तो दूसरे वृत्त की त्रिज्या होगी
(i) 10 cm
(ii) 4 cm
(iii) 3 cm
(iv) 7 cm
हल
(ii) 4 cm

प्रश्न 4.
चित्र में वृत्त का केन्द्र O है। वृत्त के बिन्दु P पर स्पर्शरखा TPT’ खींची गई है और इसके अन्तर्गत एक त्रिभुज ABP खींचा गया है। यदि ∠BPT = 60° हो, तो ∠BAP का मान क्या होगा?

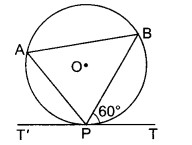
(i) 30°
(ii) 45°
(iii) 60°
(iv) 75°
हल
(iii) 60°

प्रश्न 5.
चित्र में ABCD एक चक्रीय चतुर्भुज है। वृत्त के बिन्दु B पर स्पर्श रेखा PBQ खींची गई है। यदि ∠DBQ = 110° तो ∠DAB की माप होगी

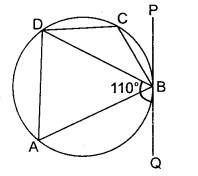
(i) 110°
(ii) 90°
(iii) 70°
(iv) 55°
हल
(iii) 70°

प्रश्न 6.
चित्र में O वृत्त का केन्द्र है। AB एक जीवा तथा AC स्पर्शी है। यदि ∠BOA = 120° हो, तो ∠BAC का मान होगा

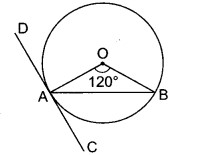
(i) 40°
(ii) 60°
(iii) 80°
(iv) 100°
हल
(ii) 60°

प्रश्न 7.
चित्र में एक वृत्त का केन्द्र O है। इस वृत्त के बाह्य बिन्द T से वृत्त पर स्पर्शरेखाएँ TP और TQ खींची जाती हैं। सम्पर्क जीवा PQ वृत्त के शेष भाग पर ∠PAQ = 70° बनाती है तो स्पर्शरेखाओं के बीच कितने अंश का कोण होगा?

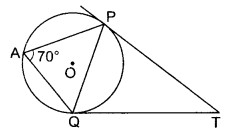
(i) 20°
(ii) 40°
(iii) 70°
(iv) 110°
हल
(ii) 40°

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
एक वृत्त की त्रिज्या 5 cm है। इस वृत्त पर किसी बाहरी बिन्दु से एक स्पर्शरेखा खींची जाती है। यदि स्पर्शरेखा की लम्बाई 12 cm है, तो बिन्दु की वृत्त के केन्द्र से दूरी ज्ञात कीजिए।

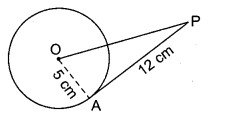
हल
दिया है : O केन्द्र वाले वृत्त में बाह्य बिन्दु P से स्पर्श रेखा PA खींची गयी है।
AP = 12 cm तथा त्रिज्या OA = 5 cm
गणना : O को A से मिलाया।
∆OAP में, ∠OAP = 90°
समकोण ∆OAP में,
OP² = OA² + AP²
⇒ OP² = (5)² + (12)²
⇒ OP² = 25 + 144
⇒ OP² = 169
⇒ OP = √169 = 13 cm
अत: बिन्दु की वृत्त के केन्द्र से दूरी 3 cm है।

प्रश्न 2.
उस वृत्त की त्रिज्या क्या होगी जिसके केन्द्र से 5.0 cm की दूरी पर स्थित एक बिन्दु से खींची गई उस वृत्त की स्पर्शरेखा की लम्बाई 3.0 cm है?

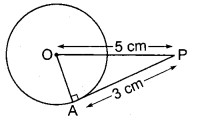
हल
दिया है : O केन्द्र वाले वृत्त में बाह्य बिन्दु P से स्पर्शरेखा AP = 3 cm
गणना : O को A से मिलाया।
तब ∆OAP में, ∠OAP = 90°
∆OAP में,
OA² = OP² – AP²
⇒ OA² = (5.0)² – (3.0)²
⇒ OA² = 25 – 9 = 16
⇒ OA = √16 cm = 4 cm
अत: वृत्त की त्रिज्या 4 cm है।

प्रश्न 3.
चित्र में AB और CD दो वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ परस्पर बिन्दु E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि AE + ED = BE + EC

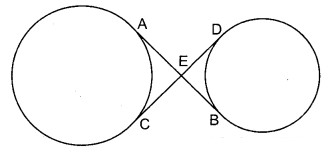
हल
AE = EC (बाह्य बिन्दु से एक ही वृत्त की स्पर्श रेखाएँ) ……… (1)
इसी प्रकार ED = EB (बाह्य बिन्दु से एक ही वृत्त की स्पर्श रेखाएँ) ………. (2)
समी० (1) व (2) को जोड़ने पर,
AE + ED = EC + EB
⇒ AE + ED = BE + EC
इति सिद्धम्

प्रश्न 4.
चित्र में, O वृत्त का केन्द्र है। वृत्त की स्पर्शरेखाओं PA तथा PB के बीच का ∠APB = 50° है, तो ∠AOB की माप ज्ञात कीजिए।

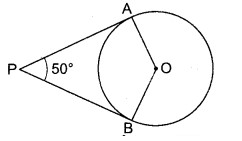
हल
∠OAP = 90° तथा ∠OBP = 90°
(स्पर्श त्रिज्या और स्पर्शरेखा के बीच बने कोण)
∴ ∠OAP + ∠OBP = 90° + 90° = 180°
∴ OAPB एक चक्रीय चतुर्भुज है।
∴ ∠AOB + ∠APB = 180°
⇒ ∠AOB = 180° – ∠APB = 180° – 50° = 130°

प्रश्न 5.
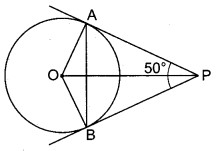
चित्र में O, वृत्त का केन्द्र है, PA और PB वृत्त की बिन्दु P से स्पर्शियाँ हैं और ∠APB = 50° तो ∠OAB की माप ज्ञात कीजिए।

हल
∆ABP में, AP = BP(बाह्य बिन्दु से स्पर्श रेखाखण्ड)
∴ ∠PAB = ∠ABP
पुनः ∠PAB + ∠ABP + ∠APB = 180°
⇒ 2∠PAB = 180° – 50° = 130°
⇒ ∠PAB = 65°
∠OAB = 90° – ∠PAB (∵ OA ⊥ AP)
⇒ ∠OAB = 90° – 65° = 25°

प्रश्न 6.
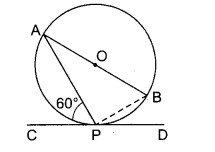
चित्र में, बिन्दु O वृत्त का केन्द्र है तथा CPD वृत्त की स्पर्शरेखा है। यदि ∠APC = 60° तो ∠BAP की माप ज्ञात कीजिए।

हल
P को B से मिलाया।
तब ∠ABP = ∠APC = 60° (एकान्तर वृत्तखण्ड में स्थित कोण)
तथा ∠APB = 90° (अर्द्धवृत्त में स्थित कोण)
∆APB में,
∠BAP = 180° – (∠ABP + ∠APB)
= 180° – (60° + 90° )
= 30°

प्रश्न 7.
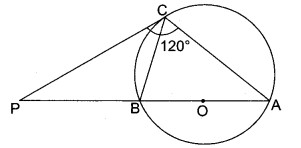
चित्र में वृत्त के बिन्दु पर खींची गई स्पर्श रेखा और व्यास AB बढ़ाने पर बिन्दु P पर मिलते हैं। यदि ∠PCA = 120°, तो ∠CBA की माप ज्ञात कीजिए।

हल
चित्र में ∠ACB = 90° (अर्द्धवृत्त में स्थित कोण)
∠PCB = 120° – 90° = 30°
पुनः ∠CAB = ∠PCB = 30° (एकान्तर वृत्त खण्ड में स्थित कोण)
∆ABC में, ∠CBA = 180° – (∠ACB + ∠CAB)
= 180° – (90° + 30°)
= 60°

लघु उत्तरीय प्रश्न

प्रश्न 1.
सिद्ध कीजिए कि किसी बाह्य बिन्दु से वृत्त पर खींची गई दो स्पर्शरेखाओं की लम्बाइयाँ बराबर होती हैं। तथा केन्द्र पर समान कोण अन्तरित करती है।
हल
दिया है : AP व AQ बिन्दु A से वृत्त C(O, r) पर खींचे गए दो स्पर्श रेखाखण्ड हैं।

सिद्ध करना है: AP = AQ तथा ∠AOP = ∠AOQ
रचना : रेखाखण्ड OA, OP और OQ खींचिए।
उपपत्ति: ∠OPA = ∠OQA = 90° (∵ वृत्त की स्पर्शरेखा स्पर्श बिन्द से जाने वाली त्रिज्या पर लम्ब होती है।)
∆OPA व ∆OQA में,
∠OPA = ∠OQA (अभी सिद्ध किया है)
OP = OQ (वृत्त की त्रिज्याएँ)
तथा OA उभयनिष्ठ है।
ΔΟΡΑ ≅ ΔOQA
AP = AQ (सर्वांगसम त्रिभुज के संगत भाग)
तथा ∠AOP = ∠AOQ

प्रश्न 2.
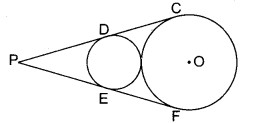
दिये गये चित्र में बाह्य स्पर्श करने वाले दो वृत्तों की उभयनिष्ठ अनुस्पर्शी रेखाएँ PDC तथा PEF खींची गई हैं जो वृत्तों को क्रमश: D व C तथा E व F पर स्पर्श करती हैं। सिद्ध कीजिए DC = EF

हल
दिया है : वृत्तों की बाह्य बिन्दु P से उभयनिष्ठ स्पर्श रेखाएँ PDC व PEF हैं।
सिद्ध करना है : DC = EF
उपपत्ति: ∵ PC व PF बड़े वृत्त की बाह्य बिन्दु P से स्पर्श रेखाएँ हैं।
PC = PF ………(1)
इसी प्रकार छोटे वृत्त के लिए
PD = PE ……….(2)
समी० (1) से (2) को घटाने पर,
PC – PD = PF – PE
DC = EF

प्रश्न 3.
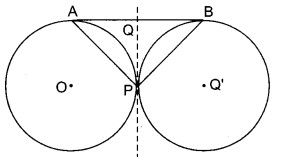
दो वृत्तों के केन्द्र O और O’ हैं जो एक-दूसरे को बाह्मतः बिन्दु P पर स्पर्श करते हैं। इन वृत्तों की एक उभयनिष्ठ स्पर्श रेखा AB खींची जाती है। सिद्ध कीजिए कि
∠APB = 90°

हल
दिया है : दो वृत्त जिनके केन्द्र O व O’ है, बाह्यतः बिन्दु P पर एक-दूसरे को स्पर्श करते हैं तथा दोनों वृत्तों की एक उभयनिष्ठ स्पर्श रेखा AB है।
सिद्ध करना है : ∠APB = 90°
रचना : बिन्दु P से दोनों वृत्तों की उभयनिष्ठ स्पर्श रेखा खींची जो AB को बिन्दु Q काटती है।
उपपत्ति : ∆BPQ में,
PQ = BQ (उभयनिष्ठ बिन्दु से वृत्त की स्पर्श रेखायें)
पुनः इसी प्रकार ∆APQ में, AQ = PQ
AQ = BQ
अर्थात् Q, AB का मध्य बिन्दु है।
अर्थात् ∆APB में शीर्ष P से खींची गयी माध्यिका सम्मुख भुजा की आधी है।
∆APB समकोण त्रिभुज है।
अर्थात् ∠APB = 90°

प्रश्न 4.
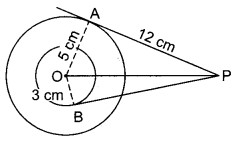
दिये गये चित्र में दो संकेन्द्रीय वृत्त जिनका केन्द्र O है तथा जिनकी त्रिज्याएँ क्रमशः 5 cm तथा 3 cm मापों की हैं। बाह्य बिन्दु P से संगत वृत्तों पर खींची गई स्पर्शियाँ PA तथा PB हैं। यदि PA = 12 cm हो, तो PB की माप ज्ञात कीजिए।

हल
O को A व B से मिलाया तब ∠OAP = 90° तथा ∠OBP = 90° तथा OA = 5 cm व OB = 3 cm
समकोण ∆OAP में,
OP² = OA² + AP² = 5² + 12² = 25 + 144 = 169
या OP = 13 सेमी
पुन: समकोण ∆OPB में
PB² = OP² – OB² = (13)² – (3)² = 169 – 9 = 160
या PB = 4√10 cm

प्रश्न 5.
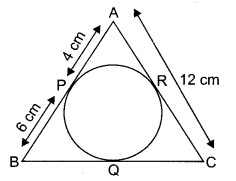
∆ABC के अन्तर्गत एक वृत्त खींचा गया है तथा P, Q, R स्पर्श बिन्दु हैं। यदि PA = 4 cm, PB = 6 cm तथा AC = 12 cm तो BC की माप ज्ञात कीजिए।

हल
चित्र में,
AP= AR = 4 cm (उभयनिष्ठ बिन्दु से वृत्त की स्पर्श रेखा)
∴ CR = AC – AR = 12 – 4 = 8 cm
पुन: CR = CQ = 8 cm (उभयनिष्ठ बिन्दु से वृत्त की स्पर्श रेखायें) तथा
तथा BP = BQ = 6 cm (उभयनिष्ठ बिन्दु B से वृत्त की स्पर्श रेखा)
∴ BC = BQ + CQ = 6 + 8 = 14 cm

प्रश्न 6.
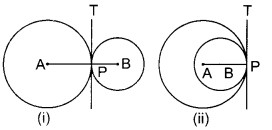
सिद्ध कीजिए कि यदि दो वृत्त एक-दूसरे को स्पर्श करते हैं तो वृत्तों के केन्द्र तथा स्पर्श बिन्दु एक रेखीय होते हैं।

हल
दिया है : दो वृत्त जिनके केन्द्र A और B हैं, एक-दूसरे को बिन्दु P पर स्पर्श करते हैं।
सिद्ध करना है : बिन्दु A, P और B संरेख हैं।
रचना : दोनों वृत्त एक-दूसरे को बिन्दु P पर स्पर्श करते हैं। अतः इनके उभयनिष्ठ बिन्दु P पर एक ही उभयनिष्ठ स्पर्श रेखा PT होगी।
बिन्दु P पर दोनों वृत्तों की उभयनिष्ठ स्पर्श रेखा PT रेखाखण्ड PA और PB खींचिए।
उपपत्ति : वृत्तों की त्रिज्याएँ AP और BP तथा उभयनिष्ठ स्पर्श रेखा PT है।
वृत्त की स्पर्श रेखा तथा स्पर्श बिन्दु से खींची गयी त्रिज्या एक-दूसरे पर लम्ब होती हैं।
∴ PA ⊥ PT और PB ⊥ PT
परन्तु किसी रेखा पर एक बिन्दु से केवल एक लम्ब खींचा जा सकता है और P से रेखा PT पर PA और PB लम्ब हैं।
अत: रेखा PA और PB संरेख हैं।
अर्थात् A, P तथा B संरेख हैं।
अतः स्पर्श बिन्दु P,रेखा AB पर स्थित है।

प्रश्न 7.
एक त्रिभुज ABC का अन्तः वृत्त त्रिभुज की भुजाओं AB, BC तथा CA को क्रमशः बिन्दुओं P, Q तथा R पर स्पर्श करता है। यदि ∠BAC = 100° तो ∠PQR की माप ज्ञात कीजिए।

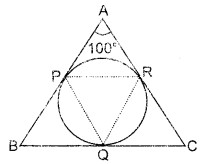
हल
रचना : PR को मिलाया।
∆APR में, AP = PR (उभयनिष्ठ बिन्दु से स्पर्श रेखाएँ)
∠APR = ∠ARP
∆APR में,
∠APR + ∠ARP + ∠PAR = 180°
⇒ 2∠ARP + 100° = 180°
⇒ ∠ARP = 40° (एकान्तर वृत्तखण्ड में स्थित कोण)
पुनः ∠PQR = ∠ARP = 40°

प्रश्न 8.
एक बाह्य बिन्दु T से एक वृत्त पर स्पर्शरेखा TP तथा एक छेदक रेखा TAB खींची गई है जो वृत्त को A और B पर काटती है। ∠APB का अर्द्धक AB को बिन्दु Q पर काटता है। सिद्ध कीजिए कि रेखाखण्ड TP = रेखाखण्ड TQ

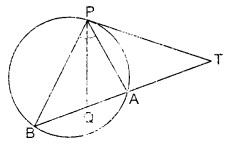
हल
दिया है : बाह्य बिन्दु T से वृत्त पर स्पर्श रेखा TP तथा छेदक रेखा TAB है जो वृत्त को A तथा B बिन्दुओं पर काटती है। PQ, ∠APB का अर्द्धक है जो AB को Q पर काटता है।
अत: ∠APQ = ∠BPQ
सिद्ध करना है : रेखाखण्ड TP = रेखाखण्ड TQ
उपपत्ति :
∠TPA = ∠PBA (एकान्तर वृत्तखण्ड में स्थित कोण)
अतः ∠TPQ = ∠TPA + ∠APQ = ∠PBQ + ∠APQ ……(1)
पुनः ∠TQP = ∠QPB + ∠PBQ (∵ ∠TQP, DBQP का बहिष्कोण है)
⇒ ∠TQP = ∠APQ + ∠PBQ ……(2)
समीकरण (1) व (2) से,
∠TPQ = ∠TQP
∆TPQ में,
रेखाखण्ड TP = रेखाखण्ड TQ (समान कोणों के सामने की भुजाएँ)

प्रश्न 9.
O एक वृत्त का केन्द्र है। दो स्पर्शरेखाएँ TP और TQ जो वृत्त को क्रमशः P और Q बिन्दुओं पर स्पर्श करती हैं। वृत्त के बाहर स्थित एक बिन्द T से खींची गई है। सिद्ध कीजिए कि ∠PTQ = 2∠OPQ

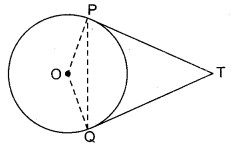
हल
दिया है : O केन्द्र वाले वृत्त के बाहर स्थित बिन्दु T से वृत्त पर स्पर्श रेखाएँ TP और TQ खींची गई है।
रचना : OP, OQ व PQ को मिलाया।
सिद्ध करना है : ∠PTQ = 2∠OPQ
उपपत्ति: ∠OPT = 90° (∵ PT बिन्दु P पर स्पर्शरेखा)
तथा इसी प्रकार ∠OQT = 90°
∠OPT + ∠OQT = 90° + 90° = 180°
चतुर्भुज के शेष कोणों ∠POQ व ∠PTQ का योग = 180°
अतः ∠POQ + ∠PTQ = 180° ………..(1)
पुन: ∆OPQ में,
∠OPQ = ∠OQP (समान भुजाओं के सामने के कोण)
∆OPQ में,
∠POQ = 180° – 2∠OPQ …….(2)
समीकरण (1) व (2) से,
180° – 2∠OPQ + ∠PTQ = 180°
⇒ 2∠OPQ = ∠PTQ

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
किसी वृत्त की जीवा PQ, उसके बिन्दु R पर खींची गयी स्पर्श रेखा ARB के समान्तर है। सिद्ध कीजिए बिन्दु R, चाप PRQ को समद्विभाजित करता है।

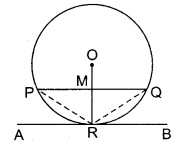
हल
दिया है : O केन्द्र वाले वृत्त में जीवा PQ है तथा वृत्त के बिन्दु R पर खींची गई स्पर्शरेखा ARB || PQ.
सिद्ध करना है : बिन्दु R, चाप PRQ को अर्द्धित करता है।
रचना : बिन्दु O को बिन्दु R से मिलाया जो PQ को बिन्दु M पर काटता है। PR व QR को मिलाया।
उपपत्ति : चूँकि स्पर्श बिन्दु से जाने वाली वृत्त की त्रिज्या स्पर्शरेखा पर लम्ब होती है।
∴ OR ⊥ AB
पुनः चूँकि PQ || AB
∴ OMR ⊥ PQ
अर्थात् ∠PMR = ∠QMR = 90°
वृत्त के केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।
PM = MQ
ΔPMR व ΔQMR में,
PM = MQ (अभी सिद्ध किया है)
∠PMR = ∠QMR (अभी सिद्ध किया है)
तथा MR उभयनिष्ठ है।
∴ ΔPMR ≅ ΔQMR
∴ PR = QR
चूँकि समान वृत्त में बराबर जीवाओं के संगत चाप बराबर होते हैं।
∴ चाप PR = चाप RQ
अर्थात् बिन्दु R चाप PRQ को अद्धित करता है।
इति सिद्धम्

प्रश्न 2.
सिद्ध कीजिए कि यदि एक रेखा वृत्त को स्पर्श करती है तो स्पर्श बिन्दु से खींची गयी जीवा और स्पर्शरेखा के बीच बने कोण संगत एकान्तर वृत्तखण्डों के कोणों के बराबर होते हैं।

हल
दिया है : केन्द्र O वाला एक वृत्त जिसके बिन्दु A पर स्पर्शरेखा PAR है तथा जीवा AB है। दो बिन्दु D और C जीवा AB के दोनों ओर वृत्तखण्डों पर स्थित हैं और D पर ∠ADB और C पर ∠ACB बना है।
सिद्ध करना है :
(i) ∠BAR = ∠BCA
(ii) ∠BAP = ∠BDA
रचना : व्यास AOE खींचा और EB को मिलाया।
उपपत्ति : वृत्त की त्रिज्या स्पर्शरेखा पर लम्ब होती है।
∠RAO अथवा ∠RAE = 90°
∠BAR + ∠BAE = 90° ……..(1)
⇒ ∠ABE = 90° (अर्द्धवृत्त में स्थित कोण)
∆ABE में,
∠BAE + ∠BEA = 90°
समीकरण (1) व (2) से,
∠BAR + ∠BAE = ∠BAE + ∠BEA
या ∠BAR = ∠BEA
परन्तु ∠BEA = ∠BCA (एक ही वृत्तखण्ड में स्थित कोण)
अत: ∠BAR = ∠BCA
इति सिद्धम्
पुनः ∠BAR + ∠BAP = 180° (∵ PAR सरल रेखा है)
तथा ∠BCA + ∠BDA = 180° (चक्रीय चतुर्भुज के सम्मुख कोण)
∠BAR + ∠BAP = ∠BCA + ∠BDA
अतः ∠BDA = ∠BAP (∵ ∠BAR = ∠BCA)
इति सिद्धम्

प्रश्न 3.
दो वृत्त एक-दूसरे को बिन्दु P पर अन्तःस्पर्श करते हैं। बड़े वृत्त की कोई जीवा AB खींची जाती है, जो छोटे वृत्त को बिन्दु पर स्पर्श करती है। सिद्ध कीजिए रेखाखण्ड CP, ∠APB का अर्द्धक है।

हल
दिया है : दो वृत्त एक-दूसरे को बिन्दु P पर अन्त:स्पर्श करते हैं।
बड़े वृत्त की कोई जीवा AB खींची गयी है जो छोटे वृत्त को बिन्दु C पर स्पर्श करती है।
AP, BP और CP को मिलाया गया है।
सिद्ध करना है : रेखाखण्ड CP, ∠APB का अर्द्धक है।
रचना : रेखाखण्ड AP छोटे वृत्त को बिन्दु D पर काटता है।
CD को मिलाया और दोनों वृत्तों की उभयनिष्ठ स्पर्शरेखा TPT खींची।
उपपत्ति: T’PT स्पर्शरेखा छोटे वृत्त को बिन्दु P पर स्पर्श करती है और PD उसकी जीवा है।
∠TPD = एकान्तर वृत्तखण्ड में स्थित ∠PCD …….(1)
इसी प्रकार बड़े वृत्त के लिए, ∠TPA = ∠PBA
∠TPD = ∠PBC …….(2)
अतः समी० (1) व (2) से, ∠PBC = ∠PCD
अब बड़े वृत्त की जीवा AB छोटे वृत्त को बिन्दु C पर स्पर्श करती है और उसकी जीवा CP है।
अत: ∠PCB = एकान्तर वृत्तखण्ड में स्थित ∠PDC ……(3)
∆PCD और ∆PBC में,
∠PBC = ∠PCD (अभी सिद्ध किया है)
∠PCB = ∠PDC (अभी सिद्ध किया है)
शेष कोण, ∠DPC = ∠BPC
अत: रेखाखण्ड CP, ∠APB का अर्द्धक है।

tense in english