bseb class 11 economics | केन्द्रीय प्रवृत्ति की माप
bseb class 11 economics | केन्द्रीय प्रवृत्ति की माप
Measures of Central Tendency)
पाठ्यक्रम (Syllabus)
विभिन्न प्रकार की औसतें जैसे-समान्तर माध्य,माध्यिका, (चतुर्थक, शतमक, बहुलक)।
इनकी गणना समान्तर माध्य, माध्यिका एवं बहुलक की सापेक्षिक स्थिति । इस अध्ययन में आप जानेंगे-
• किसी एक संख्या द्वारा आँकड़ों के समुच्चय को संक्षिप्त करने की आवश्यकता •आवृत्ति-वितरण तालिका बनाने • वर्गों के निर्माण की तकनीक
•मिलान-रेखाएँ जानने की विधि से परिचित होना
• एकचर तथा द्विचर आवृत्ति वितरण में अन्तर जानना ।
” याद रखने योग्य बातें (Points to Remember):-
1. औसत का अर्थ (Meaning of Average)-दिए गए आंकड़ों के प्रतिनिधि मूल्य को औसत कहते हैं। सांख्यिकी में औसतों का अर्थ केवल गणितीय माध्य से न होकर किसी केन्द्रीय प्रवृत्ति के माप से होता है जो विभिन्न दृष्टिकोणों से विभिन्न हो सकते हैं।
2. औसत या माध्य के प्रकार (Types of Average)-(i) समान्तर माध्य (Arithmetic Mean), (ii) माध्यि (Median). (iii) भूयिष्ठक ।
3. समान्तर माध्य (Arithmetic Mean)-इसे समान्तर औसत या माध्य भी कहते हैं। एक समंकमाला के पदों के मूल्यों के योग में उनकी संख्या से भाग देने से प्राप्त संख्या माध्य कहलाती है।
4.समान्तर माध्य के प्रकार (Types of Arithmetic Mean) -(i) साधारण समांतर माध्य,(ii) भारित समांतर माध्य ।
5. समांतर माध्य ज्ञात करने की विधि (Types of Arithmetic Mean)-(क) व्यक्तिगत समंकमाला (Individual Series)-व्यक्तिगत समंकमाला में समान्तर माध्य ज्ञात करने की दो विधियाँ हैं-
(i) प्रत्यक्ष रीति {X=£X/N} तथा लधु रीति {X=A.M.+£d/N}
(ii) विच्छिन्न तथा अवच्छिन्न समंकमाला (Discrete Series and Continuous Series)-विच्छिन्न तथा अविच्छिन्न समंकमाला में समान्तर माध्य ज्ञात करने की निम्नलिखित विधियाँ हैं-
(i) प्रत्यक्ष विधि (Direct Method)-X =Σfx/N
(ii) लघु विधि (Indirect Method): X = A.M.Σfx’/N
(iii) पद चलन विधि (Step Deviation Method)-X =A.M.Σfx/N × i
6. माध्यिका (Median)- माध्यिका समंकमाला का मध्य मूल्य होता है। इसका मूल्य किसी दी गई समंकमाला के मदों को बराबर भागों में बाँट देता है।
7. माध्यिका की गणना की विधि (Methods of Calculating Median)-व्यक्तिगत समंकमाला (Individual Series)-इस समंकमाला के अंतर्गत माध्यिका की गणना करने के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है-
M = Value of N+1/2 the Item
8. भूयिष्ठक (Mode)-समग्र में जिस मद की सबसे अधिक आवृत्ति हुई हो या पुनरावृत्ति हुई हो उसे भूयिष्ठक कहते हैं।
9. भूविष्ठक निकालने की विधि (Method of Calculating Mode)-
(क) व्यक्तिगत समंकमाला (Individual Series)-व्यक्तिगत समंकमाला में भूयिष्ठक की गणना करने के समंकमाला के सभी मदों को देख लिया जाता है और उसमें जो मद सबसे अधिक बार आया हो, वही उसका भूयिष्ठक होगा।
(ख) विच्छिन्न समंकमाला (Discrete Series)-ऐसी समंकमाला में भूयिष्ठक की गणना करने के लिए निम्नलिखित विधियाँ अपनाई जा सकती हैं-
(i) निरीक्षण द्वारा (By Inspection)-इस विधि के अनुसार दी हुई समंकमाला में उस मद को ज्ञात किया जाता है जिसकी आवृत्ति सबसे अधिक होती है तथा वह मद भूयिष्ठक कहलाता है।
(ii). समूहीकरण विधि द्वारा (By Grouping Method) -यदि दो या दो से अधिक मदों की आवृत्ति बराबर हो तो उस हाल में इस विधि का सहारा लिया जाता है । इस विधि के अनुसार दो सारणियाँ बनाई जाती हैं-(i)आवृत्ति सारणी, तथा (ii) विश्लेषण सारणी।
(iii) अविच्छिन्न समंकमाला (Indiscrete Series)-ऐसी समंकमालाओं में भूयिष्ठक ज्ञात करने के लिए दो कार्य ज्ञात करने पड़ते हैं। पहला भूयिष्ठक वर्गान्तर का पता लगाना तथा दूसरा भूयिष्ठक वर्गान्तर से भूयिष्ठक के मूल्य का पता लगाना ।
(iv) भूयिष्ठक वर्गान्तर का पता लगाना (To Find outclass-Interval of Mode)- भूयिष्ठक वर्गान्तर का पता लगाने के लिए निम्नलिखित दो विधियों में से कोई भी दो विधि अपनाई जा सकती है-
(क) निरीक्षण द्वारा (By Inspection)-जिस वर्गान्तर की आवृत्ति सबसे अधिक होती है यह भूयिष्ठक वर्गान्तर कहलाता है।
(ख) समूहीकरण विधि द्वारा (By Grouping Mehod)-यदि दो या दो से अधिक वर्गान्तर की आवृत्ति समान या लगभग समान है तथा अन्य वर्गान्तरों की आवृत्तियों में सबसे अधिक है तो उस स्थिति में भूयिष्ठक वर्गान्तर ज्ञात करने के लिए समूहीकरण विधि का प्रयोग किया जाएगा और इस विधि का प्रयोग करने के लिए वही विधि अपनाई जाएगी जिसकी वर्णन विच्छिन्न समंकमाला के अंतर्गत किया जा चुका है अर्थात् इस विधि के अंतर्गत आवृत्ति तालिका तथा विश्लेषण तालिका बनानी पड़ेगी।
(ii) भूयिष्ठक वर्गाजर में भूयिष्ठक का पता लगाना- भूयिष्ठक वर्गान्तर ज्ञात करने के बाद भूयिष्ठक का मूल्य ज्ञात किया जाता है तथा इसके लिए निम्नलिखित अंतर्गणन सूत्र का प्रयोग किया जाता है-
Z=|1+f1-fo/2f1-fo-f2×i
10. एक आदर्श औसत के आवश्यक तत्त्व (Requirements of a satisfactory average)-(i) स्पष्ट एवं निश्चित, (ii) सभी मूल्यों पर आधारित, (iii) समझने में सरल,(iv) गणना में सरलता, (v) चरम मूल्यों से प्रभावित नहीं, (vi) निरपेक्ष संख्या, (vii) बीजगणित
विवेचन संभव, (viii) न्यादर्श के परिवर्तनों का न्यूनतम प्रभाव ।
11. प्रत्यक्ष विधि द्वारा व्यक्तिगत श्रेणी में समान्तर माध्य की गणना (Calculation of Arithmetic mean by direct method)- श्रेणी के सभी मूल्यों को जोड़ना, जोड़ की श्रेणी की संख्याओं से विभाजित करना ।
12. प्रत्यक्ष विधि (Direct Method)-माध्य की कल्पना करना, उसे A द्वारा प्रकट करना, कल्पित माध्य से विचलन ज्ञात करना तथा उसे d से प्रकट करना, विचलनों को जोड़ना, उसे Σd द्वारा प्रकट करना। इसके बाद निम्न सूत्र अपनाना-
X= A=Σd\N
13. पद विचलन विधि (Step-deviation method)-माध्य की कल्पना करना, उसे A द्वारा प्रकट करना, कल्पित माध्य से विचलन ज्ञात करना तथा उसे d से प्रकट करना, पद-विचलनों को उभयनिष्ठ गुणक (common factor) से भाग देना, भजनफल को d’ से प्रकट करना,
d” का जोड़ निकालना, निम्न सूत्र का प्रयोग करके समान्तर माध्य की गणना करना-
X= A=Σd\N=C
Ed = संक्षिप्त विचलनों का जोड़
C= उभयनिष्ठ गुणांक (Common factor) .
14. चार्लियर का शुद्धता परीक्षण सूत्र (Formula of Charlier’s to Check of Accuracy)- Σf(d+1) =Σfd+Σf
15. समान्तर माध्य की गणितीय विशेषताएँ (Mathematical properties of Arthmetic mean)-
(i) समान्तर माध्य के लिए गए विचलनों का योग शून्य होता है। (ii) समान्तर माध्य के लिए गए विचलनों के वर्गों का योग अन्य किसी भी मूल्य से लिए गए विचलनों के वर्गों के योग से कम होता है। (iii) यदि श्रेणी के प्रत्येक मूल्य को समान्तर माध्य में परिवर्तित कर दिया जाता है तो उनका योगफल श्रेणी के सभी मूल्यों के योगफल के बराबर होता है।
16. सामूहिक माध्य (Combined Mean)-जब दो मदों से अधिक श्रेणियों के माध्य की गणना एक साथ की जाती है तो उसे सामूहिक माध्य कहा जाता है।
17. समान्तर माध्य, माध्यिका और बहुलक का संबंध (Relatinship between arithmetic mean, median and mode)-(i) जब वितरण सममित होता है तो बहुलक, माध्यिका और समान्तर माध्य समान होते हैं। सूत्र के रूप में Z =M=X ऐसी स्थिति में आवृत्ति वक्र का आकार एक घंटी से मिलता है।
(ii) जब वितरण असमित होता है तो आवृत्ति का आकार घंटी जैसा नहीं होता, उस समय समान्तर माध्य, माध्यिका और बहुलक तीनों का मूल्य अलग-अलग होता है। असममित वितरण के निम्न दो रूप हो सकते हैं-
(क) जब अधिक आवृत्तियाँ अन्त के मूल्यों की तरह केन्द्रित होती हैं तो बहुलक माध्यिका से बड़ा होता है और माध्यिका समान्तर माध्य से बड़ी होती है।
समीकरण के रूप में बहुलक > माध्यिका > समान्तर माध्य ।
(ख) जब अधिक आवृत्तियाँ आरंभ के मूल्यों की तरह केन्द्रित होती हैं तो उस समय समान्तर माध्य, माध्यिका और बहुलक का संबंध निम्न प्रकार होता है-
बहुलक < माध्यिका < समान्तर माध्य ।
(ii) एक साधारण रूप में असममित वितरण में X.M तथा Z का संबंध निम्न प्रकार होता है-बहुलक = 3 माध्यिका – 2 समांतर माध्यक।
18. विभाजन मूल्य (Partition Value)-यह वह मूल्य होता है जो समंक श्रेणी को दो या दो से अधिक भागों में विभाजित करता है
19. चतुर्थक (Quartiles)-यह वह मूल्य होता है जो श्रेणी को चार भागों में बाँटता है।
20. निम्न चतुर्थक (Lower Quartiles)-श्रेणी को चार भागों में बाँटने पर पहले चतुर्थन को निम्न चतुर्थक कहा जाता है।
21. ऊपरी चतुर्थक (Upper Quartiles)-श्रेणी को तीसरे चतुर्थक को ऊपरी चतुर्थक कहते हैं।
22. दशमक (Deciles)-दशमक श्रेणी को 10 बराबर भागों में बाँटने पर प्रत्येक भाग की अन्तिम इकाई को दशमक कहते हैं।
23. शतमक (Percentile)-शतमत श्रेणी को 100 बराबर भागों में विभक्त करते हैं।
एन.सी.ई.आर.टी. पाठ्यपुस्तक एवं परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्नोत्तर
( (N.C.E.R.T. Textbook and Other Important Questions for Examination)
अति लघु उत्तरात्मक प्रश्न
(Very Short Answer Type Questions)
प्रश्न 1. केन्द्रीय प्रवृत्ति के माप का अन्य नाम क्या है ?
उत्तर-सांख्यिकी माध्य।
प्रश्न 2. केन्द्रीय प्रवृत्ति के किन्हीं तीन प्रचलित मापों के नाम लिखिए।
उत्तर-(i) माध्य, (ii) माध्यिका, (iii) बहुलक ।
प्रश्न 3.समान्तर माध्य क्या है?
उत्तर-समान्तर माध्य वह मूल्य है जो किसी श्रृंखला के सभी मदों के मूल्यों के जोड़ को उनकी कुल संख्या से भाग देने पर प्राप्त होता है।
प्रश्न 4. समान्तर माध्य की गणना का सूत्र लिखिए।
उत्तर-X= ΣΧ/N
प्रश्न 5. ‘बहुलक’ किसे कहते हैं ?
उत्तर-वह मूल्य जो समंकमाला में सबसे अधिक बार आता है, बहुलक कहलाता है।
प्रश्न 6. ‘माध्यिका’ किसे कहते हैं ?
उत्तर-माध्यिका वह मूल्य है जो क्रमबद्ध समंकमाला को दो बराबर भागों में बाँटता है।
प्रश्न 7. पाँच विद्यार्थियों के किसी विषय में प्राप्तांक 11,12,13,14 तथा 15 हैं तो उनकी माध्यिका (median) क्या होगी?
उत्तर-M (माध्यिका) = 13
प्रश्न 8. एक कक्षा में 6 विद्यार्थियों के किसी विषय में प्राप्तांक क्रमशः 10, 35, 35,40, 35, 50 हैं तो बहुलक (Mode) मूल्य क्या होगा?
उत्तर-बहुलक मूल्य (Z)-35
प्रश्न 9. दस संख्याओं की समान्तर माध्य (Arithmetic mean) 18 है। यदि 3 को प्रत्येक संख्या में जोड़ दिया जाए तो नई समान्तर माध्य क्या होगा?
उत्तर-नई समान्तर माध्य=21
प्रश्न 10. गुले सिरे के वितरण में कौन-सी सांख्यिकी माव्य (Mean) की गणना करना आसान है?
उत्तर-(i) सांख्यिकी, (ii) बहुलक ।
प्रश्न 11. समान्तर माध्य (Average Mean), माध्यिका (Median) तथा बहुलक (Mode) के संबंध को व्यक्त करने वाला सूत्र लिखिए।
उत्तर-Z=3m=2X
प्रश्न 12. एक सामान्य रूप से असमानिक बंटन में समान्तर माध्य (X)=10 तथा माध्यिका (M) = 10 है तो बहुलक (Z) क्या होगा?
उत्तर-Z=30-20=10
प्रश्न 13. चतुर्थक (Quartiles) किसे कहते हैं ?
उत्तर-चतुर्थक वे मूल्य होते हैं जो क्रमबद्ध आंकड़ों को चार बराबर भागों में बाँटते हैं।
प्रश्न 14. एक व्यक्तिगत समंकमाला में समान्तर माध्य (Arithmetic mean) की गणना कैसे की जाती है?
उत्तर- X=£X/N
प्रश्न 15. दूसरे चतुर्थक (Q2) का मूल्य किस सांख्यिकीय माध्य के बराबर होता है ?
उत्तर-दूसरा चतुर्थक = माध्यिका।
प्रश्न 16. बहुलक (Mode) का बिन्दुरेखीय माप किसके द्वारा किया जाता है?
उत्तर-आवृत्ति आयत द्वारा।
प्रश्न 17. माध्यिका (Median) को बिन्दुरेखीय गणना किसके द्वारा की जाती है ?
उत्तर-संचयी आवृत्ति वक्र (ओजाइय) द्वारा।
प्रश्न 18. सामूहिक माध्य क्या है?
उत्तर-जब दो मदों से अधिक श्रेणियों के माध्य की गणना एक साथ की जाती है तो इसे सामूहिक माध्य कहा जाता है।
प्रश्न 19. बहुलक का एक लाभ लिखें।
उत्तर-वह चरम मूल्यों से प्रभावित नहीं होता।
प्रश्न 20, बहुलक को ज्ञात करते समय प्रयोग में आने वाली सारणियों के नाम लिखें।
उत्तर-(i) समूहीकरण सारणी, तथा (ii) विश्लेषण सारणी
प्रश्न 21.ओजाइब वक्र की सहायता से माध्यिका को कैसे निकाला जाता है?
उत्तर-जिस बिन्दु पर ‘से कम’ औजाइब वक्र तथा से अधिक’ ओजाइब वक्र एक दूसरे को काटते हैं, वहीं माध्यिका का निर्धारण होता है।
प्रश्न 22. क्या माध्यिका का निर्धारण रेखाचित्र के द्वारा किया जा सकता है? यदि हाँ, तो रेखाचित्र का नाम बताएं।
उत्तर- हाॅं, ओजाइव वक्र
प्रश्न 23. अखंडित श्रेणी में बहुलक ज्ञात करने का सूत्र लिखें।
उत्तर- Z=|1 f1-f2 / 2f1-f0-f2 × 1
प्रश्न 24 किस प्रकार के आवृत्ति वितरण में बहुलक का मूल्य समान्तर पाध्य से अधिक होता है?
उत्तर- ऋणात्मक विषमता वाले आवृत्ति वितरण में।
प्रश्न 25 लधु विधि और पद विचलन विधि में क्या अंतर है?
उत्तर-लधु वाधि में उभयनिष्ठ गुणक (Common factor) का प्रयोग नहीं किया जाता जबकि पद-विचलन विधि में उभयनिष्ठ गुणक (Common factor) के द्वारा विचलनों को विभाजित किया जाता है।
प्रश्न 26. यदि किसी श्रेणी में पदों की संख्या 100 है और उसका समान्तर माध्य 4 है तो श्रेणी के सभी मूल्यों का योग कितना होगा ?
उत्तर-£X=100×4=400
प्रश्न 27. निम्न श्रेणी में माध्यिका का मूल्य ज्ञात कीजिए-
2,8,7,3,9,10 तथा 6
उत्तर-7
प्रश्न 28. बहुलक ज्ञात करने के लिए समूहीकरण सारणी में कॉलमों की संख्या कितनी होती है?
उत्तर-61
प्रश्न 29. विभाजन मूल्य से क्या अभिप्राय है?
उत्तर-यह वह मूल्य है जो समंक श्रेणी को दो या दो से अधिक भागों में विभाजित करता है।
प्रश्न 30. किन्हीं चार विभाजन मूल्यों के नाम बताओ।
उत्तर-(i) चतुर्थक, (ii) दशमक, (iii) शतमत,
(iv) माध्यिका ।
प्रश्न 31. निम्न समंकों से निम्न चतुर्थक ज्ञात करें।
5,7,9,11,13,14 तथा 15
उत्तर-=N+1/4 =7+1/4=दूसरी मद = 7
प्रश्न 32. प्रथम और तृतीय चतुर्थक के वैकल्पिक नाम लिखें।
उत्तर-%Qतथा Q2
प्रश्न 33. यदि x = 25, M = 26 तो बहुलक ज्ञात करें।
उत्तर-बहुलक = 3 माध्यिका-2 माध्य
बहुलक= 3x 26-2×25 =78-50 = 28
प्रश्न 34. माध्यिका ज्ञात करें यदि समान्तर माध्य 40 व बहुलक 36 हो।
उत्तर-बहुलक = 3 माध्यिका -2 माध्य
36 = 3 माध्यिका-2×4
36 + 80=3 माध्यिका
माध्यिका = 116+3 = 38.67
प्रश्न 35. केन्द्रीय प्रवृत्ति का औसत के तीन सर्वाधिक सांख्यिकीय माप लिखें।
उत्तर-(i) समांतर माध्य, (ii) माध्यिका, तथा (iii) बहुलक प्रश्न 36. समांतर माध्य, माध्यिका एवं बहुलक की सापेक्षिक स्थिति लिखें।
उत्तर-समांतर माध्य, माध्यिका एवं बहुलक की सापेक्षिक स्थिति निम्नलिखित है-
समांतर माध्य > माध्यिका > बहुलक
बहुलक > माध्यिका अथवा समांतर माध्य ।
माध्यिका हमेशा समांतर माध्य और बहुलक के बीच में होती है
लघु उत्तरीय प्रश्न
(Short Answer Type Questions)
प्रश्न 1. निम्नलिखित तालिका में रिक्त स्थानों की पूर्ति और तालिका के बाद दिये गये प्रश्नों के उत्तर दें।
उत्तर-
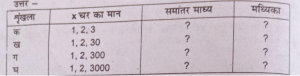
(i) क्या चरम सीमा से माध्यिका प्रभावित होती है ?
(ii) क्या माध्यिका समांतर माध्य से श्रेष्ठ विधि है ?

(i) माध्यिका चरम सीमा से प्रभावित नहीं होती।
(ii) हाँ, माध्यिका समांतर माध्य से श्रेष्ठ विधि है।
प्रश्न 2. एक श्रेणी का बहुलक ज्ञात करें जिसके समांतर माध्य तथा माध्यिका क्रमशः 16 सेमी० तथा 20 सेमी० हैं।
उत्तर – बहुलक =3 माध्यिका- 2 समांतर माध्य
= (3 x 20)-1(2 x 16)
=60-32=28 सेमी०
प्रश्न 3. यदि बहुलक 30 और माध्यिका 25 है तो समांतर माध्य ज्ञात करें।
उत्तर – बहुलक = 3 माध्यिका -2 समांतर माध्य
30=3×25-2 समांतर माध्य
2 समांतर माध्य = 75-30 = 45
समांतर माध्य = 45/2 = 22.5
प्रश्न 4. यदि किसी श्रृंखला की माध्यिका 20 सेंटीमीटर तथा माध्य 16 सेंटीमीटर हो तो भूयिष्ठक ज्ञात कीजिए।
(Median and mean of a series are 20 cm. and 16 cm. respectively. Calculate mode.)
उत्तर – भूयिष्ठक = 3 माध्यिका – 2 माध्य
या Z= 3M-2X
यहाँ M=20 सेमी.
अतएव Z=3×20-2×16
Z=60-32 = 28 सेमी.
भूथिष्ठक (Mode)Z = 28 सेमी.
प्रश्न 5. निम्नलिखित तालिका की माध्यिका ज्ञात करें-
(Calculate median from the following Table 🙂
उत्तर-माध्यिका = N+1/2 मद का मूल्य
=9+1/2= 5 वें मद का मूल्य =6
प्रश्न 6. माध्यिका के गुण लिखें ।
(Write down the merits of median.)
उत्तर – माध्यिका के गुण (Merits of Median)-
(i) इसकी गणना बहुत सरल होती है।
(ii) इसका मूल्य निश्चित होता है।
(ii) माध्यिका मूल्य चरम सीमाओं से प्रभावित नहीं होता।
(iv) गुणात्मक तथ्य जैसे-योग्यता, सुंदरता आदि के माप में अधिक सहायक होता है।
(v) यदि श्रेणी के कुछ मूल्य न भी ज्ञात हों तो माध्यिका ज्ञात की जा सकती है।
(vi) माध्यिका की गणना बिन्दु विधि द्वारा की जा सकती है।
प्रश्न 7.माध्यिका के दोष लिखें।
(Write down the demerits of median)
उत्तर-माध्यिका के दोष (Demerits of Median)-
(i) यदि श्रेणी के विभिन्न मूल्यों का वितरण अनियमित हो तो माध्यिका समूह का पूर्ण प्रतिनिधित्व नहीं करती।
(ii) इसमें श्रेणी के सभी मूल्यों को एक समान महत्त्व दिया जाता है।
(iii) इसका समान्तर माध्य की भाँति बीजगणितीय प्रयोग संभव नहीं है।
(iv) माव्यिका ज्ञात करने के लिए आँकड़ों को आरोही क्रम में क्रमबद्ध करना आवश्यक है।
प्रश्न 8. किन-किन परिस्थितियों में माध्यिका तया बहुलक प्रवृत्ति के मापों के रूप में सबसे अधिक उपयोगी है?
(In what circumstances are median and mode mostly used to measure the central tendency ?)
उत्तर-(i) खुले सिरे वाली श्रृंखला में माध्यिका तथा बहुलक की गणना आसानी से की जा सकती है जबकि समानान्तर माध्य की गणना करना कठिन है; क्योंकि ऐसे वर्गों का मध्य मूल्य निकालना संभव नहीं होता।
(ii) माध्यिका तथा बहुलक श्रेणी के चरम मूल्यों से प्रभावित नहीं होते जबकि समानान्तर माध्य पर चरम मूल्यों का प्रभाव पड़ता है।
(iii) माध्यिका तथा बहुलक का मूल्य आरेखीय विधियों जैसे-ओजाइव आवृत्ति आयत द्वारा ज्ञात किया जा सकता है जबकि समानान्तर माध्य ज्ञात करने की कोई आरेखीय विधि नहीं है।
प्रश्न 9. समान्तर माध्य केन्द्रीय प्रवृत्ति का सबसे अधिक प्रचलित माप क्यों है? कोई तीन कारण दीजिए।
(Why is Arithmetic Mean in the most popular measure of the central tendancy? Give any three causes.)
उत्तर-समान्तर माध्य केन्द्रीय प्रवृत्ति का सबसे प्रचलित माप है, क्योंकि-
(i) इसकी गणना करना आसान है तथा इसे समझना आसान है।
(ii) यह श्रेणी के सभी मूल्यों पर आधारित है।
(iii) यह प्रतिचयन के उच्चावनों के द्वारा बहुत कम प्रभावित होता है।
प्रश्न 10. समान्तर माध्य की कोई दो सीमाएं लिखिए।
(Give any two limitatioins of Arithmetic mean.)
उत्तर-समान्तर माध्य की मुख्य सीमाएं निम्न हैं-
(i) चरम मूल्यों द्वारा प्रभावित होती है। कोई भी बड़ा मूल्य या छोटा मूल्य इसे बढ़ा सकता है अथवा कम कर सकता है।
(ii) खुले सिरे के वर्गों में इसकी गणना करना संभव नहीं, क्योंकि खुले सिरे के वर्ग में मध्य मूल्य को निकालना कठिन है।
प्रश्न 11. माध्यिका तथा बहुलक में अन्तर के दो आधार बताइए।
(Give two basis of differences of Median and Mode.)
उत्तर- (i) माध्यिका निश्चित होती है जबकि बालक प्राय: अस्पष्ट और अनिश्चित होता है। कभी-कभी श्रेणी में दो या अधिक पद बहुलक हो जाते हैं।
(ii) माध्यिका उन समस्याओं का अध्ययन करने के लिए उपयोगी है जो परिणाम में व्यक्त नहीं की जा सकी हैं जैसे-स्वास्थ्य, बुद्धिमानी आदि; जबकि बहुलक विभिन्न वस्तुओं जैसे-जूते, सिले कपड़े, हैट आदि के अध्ययन के लिए उपयोगी है।
प्रश्न 12. समांतर माध्य की बीजगणितीय विशेषताएँ बताइए।
(Give the algebrical characteristics of Arithmetic Mean.)
उत्तर – समान्तर माध्य की कुछ बीजगणितीय विशेषताएँ निम्न हैं-
(i) किसी श्रेणी के विभिन्न पद मूल्यों के समानान्तर माध्य में निकाले गए विचलनों का प्रयोग शून्य होता है अर्थात्
£ (X-X)=0
(ii) किसी श्रेणी के समानान्तर माध्य से निकाले गए विचलनों के वर्गों का योग न्यूनतम होता है।
£(X-X)² = न्यूनतम
(iii) किसी श्रेणी के दो अथवा अधिक भागों के पद मूल्यों की संख्या तथा समानान्तर माध्य ज्ञात होने पर समानान्तर माध्य ज्ञात हो जा सकती है, अर्थात्
X12= X1N4 + X2N2/ N1+N2
प्रश्न 13. आठ परिवारों की दैनिक आय निम्नलिखित है-
170, 500, 250, 700, 400, 200, 350
परिवार की औसत दैनिक आय (Average daily income) निकालिए।
उत्तर-समान्तर माध्य की गणना (Calculation of Arithmetic Mean)
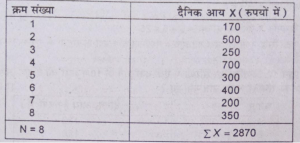
X= £X/N = 2870/8= 358.75
प्रश्न 14. एक कक्षा के 50 छात्रों की औसत 61 इंच है तथा दूसरी कक्षा के 70 छात्रों की औसत ऊँचाई 58 इंच है । दोनों कक्षाओं के सभी छात्रों की सामूहिक ऊँचाई ज्ञात करें।
उत्तर-दिया है n। = 50,X1 = 61,n2 = 70.X= 58
X1.2 =50×61+70×58\ 50+70= 3050+4060/120= 7110/120= 59.25 इंच
प्रश्न 15. एक छात्र के सीनियर सेकंडरी परीक्षा में अंग्रेजी में 60%, हिन्दी में 75% तथा गति में 63% अंक हैं । यदि इन विषयों का भार क्रमश: 1,1 तथा 2 है तो भारित समान्तर माध्य (Weighted Arithmetic Mean) निकालें।
उत्तर-
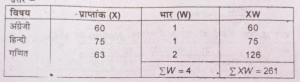
:• Xw = 261/4= 65.25
अतः भारित समान्तर माध्य = 65.25 अंक ।
प्रश्न 16. सिद्ध करें कि मध्यमान तथा चरों की संख्या का गुणनफल चरों के मूल्य के योग के बराबर होता है।
उत्तर-
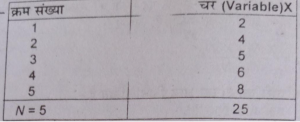
5 मदों का योगफल = 25
मध्यमान = 25/5=5
मध्यमान X मदों की संख्या = 5×5=25
अतः सिद्ध हुआ कि मदों का योग = मध्यमान तथा मदों के संख्या के गुणनफल के बराबर होता है।
प्रश्न 17. निम्नलिखित सारणी में एक कारखाने के 10 मजदूरों की दैनिक आय दी गई है। इनका समांतर माध्य ज्ञात कीजिए?

उत्तर-X/ X1+X2 + X3+…….Xn /N
X= 120 + 150 + 180 + 200 + 300 +220 +350 + 370 + 260 / 10
=2400/10 = 240 रुपए
प्रश्न 18. निम्न आँकड़ों की सहायता से माध्यिका (Median) ज्ञात कीजिए-
उत्तर-

माध्यिका= {N+1\2} वें मद का मूल्य
={60+1\2} वें मद का मूल्य
= 30.5 वें मद का मूल्य
= 30.5वें मद का मूल्य 35 संचयी आवृत्ति में है। अतः माध्यिका = 60
प्रश्न 19. पाँच परिवारों की मासिक आय नीचे दी गई है-
6550, 7550,9550,4550 तथा 8000
लघु विधि से माध्य की गणना करें।
उत्तर-
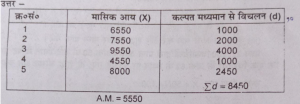
X = A.M.+£d/N
= 5550 +8450/5 = 5550 + 1690 = 7240.
प्रश्न 20. प्रत्यक्ष विधि से निम्नलिखित वितरण का समान्तर माध्य (Arithmetic mean) ज्ञात करें।

उत्तर-
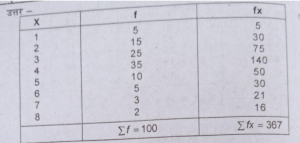
x=£fx\£f= 367/100 = 3.67
प्रश्न 21. गलत मूल्य लिखने के कारण अशुद्ध समान्तर माध्य से शुद्ध समान्तर माध्य की गणना कैसे करेंगे?
उत्तर-गलत मूल्य लिखने के कारण अशुद्ध समान्तर माध्य से शुद्ध समांतर माध्य की गणना में निहित चरण (Steps involved in calculating correctA.M. from incorrect A.M. due to writing incorrect value) –
(i) अशुद्ध समांतर माध्य को संख्या (N) से गुणा करें अर्थात् XxN
(ii) X×N से गलत मूल्य को घटाएँ और सही मूल्य को जोड़ें।
(iii) जोड़ को N से भाग करें और शुद्ध समांतर माध्य प्राप्त करें।
प्रश्न 22.100 विद्यार्थियों द्वारा प्राप्त औसत अंक 50 के बाद स्थान में यह ज्ञात हुआ कि एक विद्यार्थी के अंक 63 के स्थान पर 93 पढ़े गए, तो शुद्ध औसत अंत क्या होंगे?
उत्तर-दिया गया X = 50N = 100
X= ΣΧ/ N
50 =ΣΧ/100
:• ΣX = 5000
अशुद्ध अंक (93) को निकाल कर और शुद्ध अंक (63) को जमा करके शुद्ध
ΣΧ=5000-91+63=5970
शुद्ध X= 4970/100=49.70
प्रश्न 23. किसी कक्षा के 100 विद्यार्थियों के माध्य अंक 48 हैं । जाँच करने के बाद पता चला कि किसी एक विद्यार्थी के अंक 53 के स्थान पर 73 जोड़ लिए गए हैं । सही समान्तर माध्य ज्ञात करें।
उत्तर-
अशुद्ध ΣX = N×X = 100 x 48 = 4800
शुद्ध ΣΧ = 4800-73+ 53 = 4780
अतः शुद्ध समांतर माध्य (X) =ΣΧ/N =4780/100=47.8 अंक
प्रश्न 24. 5 मदों का समांतर माध्य 7 है, किन्तु जाँच करने पर मालूम हुआ कि दो मदें 5 और 9 के स्थान पर 4 और 8 ले ली गई। सही समांतर माध्य ज्ञात करें।
उत्तर-अशुद्ध £X-7×5=35
शुद्ध £X = 35-4-8+5+9 = 37
समांतर माध्य X=£X/N=37×5=7.4
प्रश्न 25. समांतर माध्य को चरों के मूल्यों के वितरण का गुरुत्वाकर्षण केन्द्र क्यों कहा गया है ? समझाएँ।
उत्तर-समांतर माध्य की गणना करने के लिए हम सभी चरों के मूल्यों को लेते हैं। उनके जोड़ को चरों की संख्या से विभाजित करते हैं। समांतर माध्य से धनात्मक विचलनों का योगफल ऋणात्मक विचलनों के जोड़ के बराबर होता है। दूसरे शब्दों में हम कह सकते हैं कि धनात्मक तथा ऋणात्मक विचलन एक दूसरे को संतुलित करते हैं। इसका तात्पर्य यह हुआ कि समांतर
माध्य चरों के मूल्यों के वितरण का गुरुत्वाकर्षण केन्द्र है।
प्रश्न 26. मान लो माध्यिका का मूल्य 26 है और समांतर माध्य का मूल्य 25 है तो ऐसी अवस्था में बहुलक का मूल्य क्या होगा?
उत्तर-बहुलक = 3 माध्यिका-2 समांतर माध्य
= 3 x 26-2 x 25
= 78 – 50 = 28
प्रश्न 27. समांतर माध्य की एक विशेषता यह है कि यह बहुत बड़े या बहुत छोटे मूल्य से प्रभावित होता है। उदाहरण की सहायता से यह प्रमाणित करें।
उत्तर-उदाहरण के लिए हम नीचे 5 श्रमिकों की दैनिक मजदूरी लेते हैं-
45,55,55,65,70 रुपए
इनका समांतर माध्य (x) =£X/N=290/50= 58 रुपए
अब हम मान लेते हैं कि एक ओर श्रमिकों की दैनिक मजदूरी 100 रु० है तो ऐसी अवस्था में समांतर माध्य
X=290+190/5+1 =480/6 = 80 रुपए
उदाहरण से यह सिद्ध होता है कि एक बड़ी संख्या लेने से समांतर माध्य काफी प्रभावित हुआ। (पहले यह 58 रुपये था अब यह 80 रुपए है।)
प्रश्न 28. निम्नलिखित तालिका से भारित माध्य ज्ञात करें-
उत्तर-

प्रश्न 29. मान लो 5 मदों की एक श्रेणी का समांतर माध्य5है। उनमें चार मदों का मूल्य क्रमशः 10, 15, 30 और 35 है । श्रेणी के 5वें मद का लुप्त मूल्य ज्ञात करें।
उत्तर-माना लुप्त मूल्य =X5
अतः X= 10+15+30+35+X5/N5 =90+X5/5
30 =90+X5/5
अर्थात् 90+X5 =150 X5=150-90=60
अत: लुप्त मद का मूल्य =60 है।
प्रश्न 30. एक विद्यार्थी के अंग्रेजी में 60 अंक, हिन्दी में 75, गणित में 63, अर्थशास्त्र में 59 तथा सांख्यिकी में 55 अंक आए । अंकों का भारित औसत ज्ञात करें यदि भारित औसत क्रमश: 2,1,5.5 तथा 3 हो।
उत्तर-

प्रश्न 31. निम्न तालिका की सहायता से सामूहिक समान्तर माध्य ज्ञात करें-
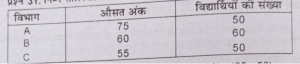
उत्तर-सामूहिक समांतर माध्य
=(75×50) + (60×60) + (55×50)/50 +60 + 50
= 3750 + 3600+2750/160 =10.100/160
= 63.125 अंक
प्रश्न 32. एक कार्यस्थल पर 50 आदमी, 20 औरतें और 10 बच्चे कार्य करते हैं। उनकी मजदूरी 8 रुपए, 6 रुपए और 4 रुपए प्रति घंटा है। उनकी प्रति घंटा दैनिक मजदूरी की गणना करें।

XW=£WX/£W= 560/80 =7 रुपये प्रति घंटा
प्रश्न 33. उदाहरण से सिद्ध करें कि माध्यिका से विचलनों का योगफल (±चिह्न ध्यान में रखते हुए दूसरे बिन्दु के विचलनों को जोड़ से कम होता है।
उत्तर-
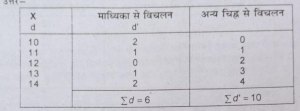
माध्यिका= N+1/2 मद का मूल्य =5+2/2
= तीसरे मद का मूल्य = 12
अन्य बिन्दु (माना) = 10
यहाँ पर मध्यिका से विचलनों का जोड़ (£d) = 60 और अन्य बिन्दु (10) से विचलनों का जोड 10 है।
अत: सिद्ध हुआ कि माध्यिका से विचलनों का योगफल अन्य बिन्दु से विचलनों के योगफल से कम है।
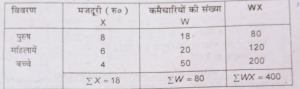
प्रश्न 34. उदाहरण से सिद्ध करें कि भारित समांतर माध्य साधारण समांतर माध्य से कम होगा तब कम मूल्य वाली पदों को अधिक भार दिया जाता है और अधिक मूल्य वाले मदों को कम।
उत्तर-प्रश्न में दिए गए कथन को सिद्ध करने के लिए हम निम्न तालिका लेते हैं-
दीर्घ उत्तरात्मक प्रश्न
(Long Answer Type Questions)
प्रश्न 1. यदि नीचे दिए गए आंकड़ों का समांतर माध्य (Arithmetic mean) 28 है, तो-
(क) लुप्त आवृत्ति का पता करें और (ख) श्रृंखला की माध्यिका ज्ञात करें।

उत्तर-लुप्त आवृत्ति
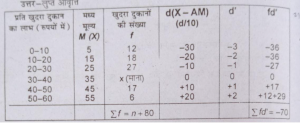
A.M =35
X=AM+£fd/£f×C= 35+ -70/n+80×10 =35+700/n+80
अत:35-700/n+80= 28 (दिया हुआ है।)
अथवा,-700/n+80= 28-35/1= -7/1
अथवा, 100/n+80=1
अथवा n+80=100 अथवा n=100-80=20
अतः आवृत्ति 20 है।
माध्यिका गणना (Calculation of Median)
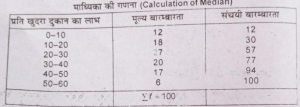
M माध्यका=N/2 का मूल्य=100/2= 50 वें मद का मूल्य । यह मूल्य 20-30 वर्गान्तर में आता है।
N
50 – 30
माध्यिका = l¹ +N/2-cf/f×1 =20+50-30/27×10
= 20+200/27*20+7.41= 27.41 उत्तर
प्रश्न 2. निम्न श्रृंखला किसी कंपनी में नियोजित मजदूरों की दैनिक आय से सम्बद्ध है। अभिकलन कीजिए-(क) निम्नतम 50 प्रतिशत मजदूरों की उच्चतम आय, (ख) शीर्ष 25 प्रतिशत मजदूरों द्वारा अर्जित न्यूनतम आय और (ग) निम्नतम 25 प्रतिशत मजदूरों द्वारा अधिकतम आय।
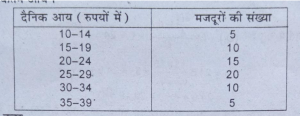
उत्तर

माध्यिका =N/2 मद का मूल्य=65/2= 32.5 मद का मूल्य
32.5 मद का मूल्य 24.5-29.5 में निहित है।
माध्यिका =l¹+N/2-cf/f×1
= 24.5+ 32.5-30/20×5
=24.5+2.5/70×5= 24.5+32.5-30/20×5
24.5+0.6=25.11
प्रथम चतुर्थक Q1={N/4}मद का मूल्य
65/4=16.25 वें मद का मूल्य
1625 मद का मूल्य 19,5-24.5 वर्गान्तर में निहित है।अत: Q1= 1¹ +N/4-cf/f×i =19.5+(16.25-15/15)×5
=19.5+1.25/3×5 =19.5+1.25/3 =19.5+0.42=19.92 उत्तर।
तृतीय चतुर्थक (Q3)=(3N/4) मद का मूल्य
=65×3\4= 195/4= 48.75 मंद का मूल्य
48.75 मद का मूल्य 24.5-29.5 वर्गान्तर में है।
अतः तृतीय चतुर्थक (Q1) = I+3N/4-cf/f×1=24.5+48.75-30/
=24.5+18.75/20×5
=24.5+18.75/4
=24.9+4.69=29.19 उत्तर
प्रश्न 3. नीचे एक गाँव के 380 परिवारों की जोतों का आकार दिया गया है । जोत का माध्यिका ज्ञात कीजिए।
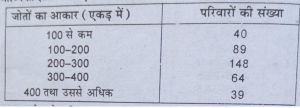
उत्तर-जोत के माध्यिका आकार की गणना (Calculation Meidan Size of Holding)

मध्यिका=N/2 मद का मूल्य =65/2 =190 वें मद का मूल्य
अत: मद का मूल्य 200-300 वर्गान्तर में स्थित है।
मध्यिका =1¹+(N/2-cf/f)×h
= 200+(190-129\148)×100
= 200 +(61/148 x100)
= 200+(6100/148) = 200 +41.21 = 241.21 एकड़
प्रश्न 4. निम्नलिखित सूचना 150 परिवारों की दैनिक आय से संबद्ध है । समांतर माध्य का परिकलन कीजिए।

उत्तर-पहले से अधिक संचयी बारम्बारता की वर्ग आवृत्तियाँ ज्ञात करें।
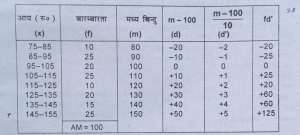
X=A(£fd’/N)×C
=100+(245/150)×10
=100+16.33=116.33.
प्रश्न 5. केन्द्रीय प्रवृत्ति से आप क्या समझते हैं ? सांख्यिकीय माध्य के उद्देश्य तथा कार्य क्या हैं ?
(What do you mean by central tendency ? What are the functions and objectives of statistical averages?)
उत्तर-केन्द्रीय प्रवृत्ति का आशय (Meaning of Central Tendency)-एक समंकमाला की केन्द्रीय प्रवृत्ति का आशय उस समंकमाला के अधिकांश मूल्यों की किसी एक मूल्य के आस-पास केन्द्रित होने की प्रवृत्ति से है। किसी समंकमाला या आवृत्ति वितरण में शीर्ष मूल्य तो कम ही होते हैं, अधिकांश मूल्य पदमाला के मध्य में ही केन्द्रित रहते हैं। उदाहरणत: यदि किसी कक्षा में सांख्यिकी अध्ययन करने वाले विद्यार्थियों की कोई परीक्षा ली जाए तो परीक्षार्थियों में बहुत अच्छे और बहुत कम अंक प्राप्त करने वाले छात्र तो कम होंगे, अधिकांश छात्रों के प्राप्तांक पूर्णाकों के 50% के आस-पास रहेंगे। स्वाभाविक है कि यह केन्द्रीयकरण लगभग बीच के मूल्यों में ही निहित होता है। ये केन्द्रीय मूल्य ही केन्द्रीय
प्रवृत्ति की माप अथवा माध्य कहे जाते हैं, इस प्रकार माध्य सम्पूर्ण समंकमाला का एक प्रतिनिधि मूल्य होता है और इसलिए इसका स्थान सामान्यतया श्रेणी के मध्य में ही होता है । क्रॉक्स्टन एवं काउडेन (Croxtpm & Cowder) के शब्दों में, “माध्य समंकों के विस्तार के अंतर्गत स्थित एक ऐसा मूल्य है जिसका प्रयोग श्रेणी के सभी मूल्यों का प्रतिनिधित्व करने के लिए किया जाता है । समंकमाला के विस्तार के मध्य
में स्थित होने के कारण ही माध्य को केन्द्रीय मूल्य माप भी कहा जाता है।”
(“An average is a single value within the range of the data that is used to represent all of the yalues in the series. Since an average is somewhere
within in the range of data, it is sometimes called a measure of central value.”)
इसी प्रकार ए० आई० वॉघ (Waugh) के शब्दों में, एक माध्य मूल्यों के एक समूह से चुनागया वह मूल्य है जो उसका किसी रूप में प्रतिनिधित्व करता है-एक ऐसा मूल्य है जो पूर्ण समूह के मूल्यों के प्रतिरूप में है जिसका वह एक अंश है।” (“An average is a single value selected from a group of Values to present them in some way a value which is supposed to spot for whole group of which it is part or thpical of all the values in the group.)
सांख्यिकीय माध्यों के उद्देश्य एवं कार्य
(Objects and Functions of Statistical Averages)
सांख्यिकीय माध्यों के मुख्य उद्देश्य व कार्य निम्नलिखित हैं-
(i) समंकों का संक्षिप्त चित्र प्रस्तुत करना (To present a brief picture of the entire data)-माध्यों द्वारा जटिल और अव्यवस्थित समंकों की मुख्य विशेषताओं का सरल, स्पष्ट एवं संक्षिप्त चित्र प्रस्तुत किया जाता है। इससे उन समंकों को समझना व याद रखना बहुत
सुगम हो जाता है। उदाहरणार्थ, 102 करोड़ भारतवासियों की अलग-अलग आयु को याद रखना
एक असंभव-सी बात है, परन्तु औसत आयु प्रत्येक व्यक्ति याद रख सकता है । इसी प्रकार 102 करोड़ व्यक्तियों की आयु के समंक याद रखना असंभव है, लेकिन औसत आयु सुगमता से याद रखी जा सकती है। अत: माध्य समंकों का विहंगम दृश्य (Bird’s eye view) प्रस्तुत करते हैं। मोरोन (Moroney) ने ठीक ही कहा है, “माध्य का उद्देश्य व्यक्तिगत मूल्यों के समूह का सरल
और संक्षिप्त रूप से प्रतिनिधित्व करना है जिससे कि मस्तिष्क समूह की इकाइयों के सामान्य आकार को शीघ्रता से ग्रहण कर सके।”
(The purpose of average is to represent a group of individual values in a simple and concise manner so that the mind can get a quick understanding
he general size of the individual in the group.”)
(ii) तुलना में सहायक होना (To facilitate comparison)-माध्य समंकों की समस्त राशि को संक्षिप्त व सरल करके तुलना योग्य बनाते हैं । समंक की तुलना से बहुत महत्त्वपूर्ण निष्कर्ष निकाले जा सकते हैं। उदाहरण के लिए विभिन्न देशों की औसत आयु की तुलना से ज्ञात किया जा सकता है कि कौन-सा देश सबसे अधिक समृद्धिशाली है तथा कौन-सा सबसे कम।
(iii) उपयुक्त नीतियों के निर्धारण में सहायक होना (To help in the formulation of suitable policies)-माध्य उपयुक्त नीतियों के निर्धारण में बहुत अधिक सहायक होते हैं। उदाहरण के लिए यदि किसी विद्यालय में बी०ए० क तृतीय वर्ष की चार कक्षाओं के ‘क’ ‘ख’,
‘ग’ एवं ‘घ’, के विद्यार्थियों के किसी विषय में औसत नंबर इस प्रकार हैं- 60,58, 40 एवं 55 तो इससे यह निष्कर्ष निकलेगा कि कक्षा ‘ग’ के विद्यार्थी इस विषय में बहुत कमजोर हैं और उनकी कमी को दूर करने के लिए विशेष प्रबंध करना आवश्यक है।
(iv) सांख्यिकीय विश्लेषण का आधार (Basis of Statistical Analysis)-सांख्यिकीय विश्लेषण की अनेक क्रियाएँ माध्यों पर आधारित हैं।
प्रश्न 6. आदर्श माध्य के आवश्यक गुण लिखें।
(Write down the requirements of a model average.)
उत्तर-आदर्श माध्य के आवश्यक गुण (Requirements of amodel average)-एक आदर्श माध्य के निम्नलिखित गुण होने चाहिए-
(i) समझने में सरल (Easy to understand)-सांख्यिकीय विधियों का प्रयोग समंकों को संक्षिप्त तथा सरल बनाने के लिए किया जाता है। अत: माध्य ऐसा होना चाहिए जो आसानी से समझा जा सके, अन्यथा इसका प्रयोग बहुत ही सीमित होगा ।
(ii) समझने में सरल (Easy to Compute)-माध्य की गणना-क्रिया सरल होनी चाहिए ताकि इसका प्रयोग व्यापक रूप से हो सके । यद्यपि माध्य का निर्धारण जहाँ तक हो सके सरल होना चाहिए तथापि विशेष परिस्थितियों में परिणाम की शुद्धता के लिए अधिक कठिन माध्यों का प्रयोग भी किया जा सकता है।
(iii) श्रेणी के सभी मूल्यों पर आधारित (Based on all the items of the series)-माध्य श्रेणी के सभी मूल्यों पर आधारित होना चाहिए ताकि एक या अधिक मूल्यों
में परिवर्तन होने से माध्य में परिवर्तन हो सके। यदि माध्य श्रेणी के सभी मूल्यों पर आधारित नहीं है तो वह
समूह का प्रतिनिधित्व ठीक प्रकार से नहीं कर सकता।
(iv) न्यूनतम तथा अधिकतम मूल्यों पर अनुचित प्रभाव से बचाव (Should not be unduly affected by Extreme items)-यद्यपि माध्य सभी मूल्यों पर आधारित होना चाहिए तथापि किसी विशेष मूल्य पर अधिक प्रभाव नहीं पड़ना चाहिए अन्यथा माध्य समंकों का सही रूप व्यक्त नहीं करेगा।
(v) स्पष्ट व स्थिर (Rigidly defined)-माध्य की परिभाषा स्पष्ट शब्दों में व्यक्त होनी चाहिए ताकि जो भी व्यक्ति दिए हुए समंकों से माध्य निकाले वह एक निष्कर्ष पर पहुँचे । इसके लिए यह आवश्यक है कि माध्य गणितीय सूत्र के रूप दिया जाए। यदि माध्य की गणना में व्यक्तिगत प्रवृत्तियों का प्रभाव पड़ा तो फल भ्रामक तथा अशुद्ध होंगे।
(vi) बीजगणितीय विवेचना संभव (Capable of algebrate treatment)-एक अच्छे माध्य का बीजगणितीय विवेचन संभव होना चाहिए । उदाहरण के लिए यदि दो कारखानों में मजदूरों की संख्या तथा उनकी औसत आय से संबंधित समंक दिए गए हों तो दोनों कारखानों के मजदूरों की आय का सामूहिक माध्य निकालना संभव होना चाहिए।
(vii) न्यादर्शों की भिन्नता का कम से कम प्रभाव (Least effects of flucuations of sampling)-यदि एक ही समय में से उचित रीति द्वारा विभिन्न न्यादर्श लेकर माध्य निकाले जाएं तो उन माध्यों में बहुत अधिक अंतर नहीं होना चाहिए। उदाहरण के लिए, यदि एक विश्वविद्यालय के विद्यार्थियों को 10 भागों में बाँट कर 10 न्यादर्श लिए गए हैं तो उनके परिणामों में बहुत अधिक असमानता नहीं होनी चाहिए।
प्रश्न 7. माध्य या औसत क्या है ? इसके उद्देश्य (कार्य) क्या ?
(What are average ? What are its objectives Functions ?)
उत्तर-श्रेणी की केन्द्रीय प्रवृत्तियों की माप को माध्य या माप औसत कहते हैं । माध्य एक श्रेणी का प्रतिनिधि अंक होता है। यह एक अंकगणितीय विधि है जिसके द्वारा परिणाम संक्षेप में व्यक्त किया जाता है और वह परिणाम पूरी श्रेणी का प्रतिनिधित्व करता है। केन्द्रीय प्रवृतियों के माप या माध्यों का आर्थिक विश्लेषण में बहुत महत्वपूर्ण स्थान है। यहाँ तक की सांख्यिकी औसतों को विज्ञान कहकर परिभाषित किया जाता है।
माध्य या औसत निम्नलिखित तीन प्रकार के होते हैं-
(i) समांतर माध्य (Arithmetic Mean), (ii) मध्यिका (Median), (iii) उभयप्टिक या बहुलक (Mode)।
औसतों या माध्यमों के उद्देश्य (कार्य)-
(i) सरलीकरण तथा संक्षिप्तीकरण (Simplication)- माध्यों की सहायता स विशाल आँकड़ों को सरल एवं संक्षिप्त रूप में प्रस्तुत किया जा सकता है। उदाहरणार्थ दश के प्रत्येक व्यक्ति की आय को याद रखना संभव नहीं है, परन्तु प्रति व्यक्ति आय को याद रखना और समझना आसान है । इसी प्रकार औसत आयु. औसत अंक औसत वेतन जैसे जटिल आँकड़ों को संक्षिप्त
और सरल रूप में प्रस्तुत करत हैं।
(ii) तुलना में सहायक (Helpful in comparison)- माध्यकों की सहायता से दो तथ्यों की तुलना करना आसान हो जाता है। उदाहरणार्थ दों देशों की औसत
आयु की तुलना करके उनकी आर्थिक दशा का पता लगाया जा सकता है।
(iii) भावी योजनाओं में सहायक (Helpful in future planning)-व्यापारी, अर्थशास्त्री आदि माध्यों के आधार पर महत्वपूर्ण निर्णय लेते हैं और इस प्रकार से ये उनकी भावी योजनाओं के निर्माण में सहायक होते हैं।
(iv) माध्यों द्वारा व्यक्तिगत व बिखरं तथ्यों को आसानी से समझा जा सकता है।
प्रश्न 8. समान्तर माध्य किसे कहते हैं ? इनकी विशेषताएँ लिखें।
(What is arithmetic mean ? Write down its special features.)
उत्तर-समान्तर माध्य (Arithmetic mean)-समान्तर माध्य से अभिप्राय उस मूल्य से है जो किसी श्रेणी के समस्त मूल्यों के योग को उनकी इकाइयों की संख्या से भाग देने पर प्राप्त होता है । समान्तर माध्य केन्द्रीय प्रवृनि का सबसे उत्तम माप माना जाता है । यह सबसे अधिक प्रचलित माप है। उदाहरण के लिए 2.4.8.14 का समान्तर माध्य =2 + 4 + 8 + 14\4 =7 है।
समान्तर माध्य की विशेषताएँ (Special features of Arithmetic Mean)-समांतर माध्य की विशेषताएँ निम्नलिखित हैं-
(i) समान्तर माध्य से लिए गए विचलनों का बांग शून्य होता है। समीकरण में,£(X-X)=0
(ii) मान लें कुछ परिवारों की मासिक आयु के बारे में चिन्तन कर रहे हैं । यदि कुल आय का वितरण समान है तो समान्तर माध्य हमें यह आयु देगा जो प्रत्येक परिवार प्राप्त करेगा।
मान लो कुल आयु = 40,000 रुपए
परिवारा की संख्या =8
समान्तर माध्य= 40,000+8= 5.000
अत: प्रत्येक परिवार की आय 5000 रुपए होगी यदि आय का वितरण समान है।
(iii) समान्तर माध्य को अंकगणितीय विशेषता निकालना सरल है
(iv) समान्तर माध्य की गणना करने के लिए हम सभी चरों के मूल्य को लेते हैं । किसी चर के मूल्य का नहीं छोडते ।
(v) समान्तर माध्य बहुत बड़े या बहुत छोटे मूल्य से प्रभावित होते हैं। उदाहरण के लिये एक मुहल्ले के 5 परिवारों का देनिक व्यय 25, 28, 32, 27 तथा 33 रुपए है। ऐसी अवस्था में समान्तर माध्य 29 रुपए होगा। मान ला उस मुहल्ले में एक धनी परिवार आकर बस जाता है। उस परिवार का दैनिक व्यय 125 रुपए है। यदि हम दोबारा समान्तर माध्य की गणना करें तो समान्तर माध्य 45 आएगा। इस तरह समान्तर माध्य एक बड़े मूल्य से काफी प्रभावित हुआ और समान्तर माध्य 29 रुपए से बढ़कर 45 रुपए हो गया।
(vi) यदि श्रेणी के प्रत्येक मूल्य को समान्तर माध्यक में परिवर्तित कर दिया जाता है तो उसका योगफल श्रेणी के सभी मूल्यों के योगफल के बराबर होता है। समीकरण में XN= £X इस निम्न उदाहरण की सहायता से समझाया जा सकता है-

X=25/5=5
इस प्रकार यदि हमें श्रेणी का समान्तर माध्य तथा पद मूल्यों की संख्या ज्ञात है तो समूह का £X प्राप्त कर सकते हैं।
(vii) समान्तर माध्य से लिय गये विचलनों के वर्गों का योग अन्य किसी मूल्य से निकाले गये विचलनों के वर्गों के योग से कम होता है।
प्रश्न 9. निम्नलिखित सूचना के आधार पर प्रत्यक्ष विधि (Direct Method) पद विचलन विधि (Step Deviation Method) तथा कल्पित माध्य विधि (Assumed Mean Method) से समान्तर माध्य ज्ञात करें।
(Find the mean of the following data with the help of arithmetic mean. step deviation and assumed mean method.)
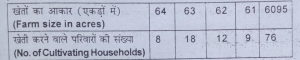
उत्तर-(i) प्रत्यक्ष विधि से मध्यमान की गणना
(Calculation of Arithment mean by Direct Method)

X=3713/60=6188 एकड़
(ii) कल्पित माध्य विधि से समान्तर माध्य की गणना
(Calculation of Arithmetic Mean by Assumed Mean)
प्रत्येक विधि से समान्तर माध्य 61.88 एकड़ है। अत: हम प्रश्न विधि से निकालने के लिए, कल्पित समान्तर माध्य 62 लेते हैं।

X= A.M +(fd/N) = 62-(6/7)
= 62 -0.113 = 61.884 = 61.88
प्रश्न 10. समान्तर माध्य के गुण तथा दोष लिखिए।
(Write down the merits and demerits of arithmetic mean.)
उत्तर-(i) समांतर माध्य की गणना सरल है।
(ii) इमसें बीजगणित का प्रयोग किया जाता है।
(iii) इसकी गणना में सभी मदों का प्रयोग किया जाता है।
(iv) यह आर्थिक विश्लेषण में सबसे अधिक प्रचलित है।
(v) यह तुलना के लिए एक अच्छा आधार है।
(vi) इसका निर्धारण उस समय भी संभव है जब केवल श्रेणी के मूल्यों और उनका योग मालूम हो।
(vii) इसका मूल्य सदैव निश्चित होता है।
(viii) यह अधिक विश्वसनीय माप ।
(ix) इसकी गणना करने के लिए आँकड़ों को व्यवस्थित करने की कोई आवश्यकता नहीं होती।
समान्तर माध्य के दोष (Demerits of Arithmetic Mean)-समान्तर माध्य के दोष निम्नलिखित हैं-
(i) समान्तर माध्य चरम सीमाओं अर्थात् अधिकतम व न्यूनतम मूल्यों से प्रभावित होता है।
(ii) गुणात्मक श्रेणी के लिए इसका प्रयोग नहीं किया जाता।
(iii) किसी मद के अनुपस्थित होने पर इसकी गणना अशुद्ध होगी।
(iv) समान्तर माध्य का निर्धारण केवल अवलोकनों द्वारा नहीं किया जाता।
(v) यह श्रेणी का एक सच्चा प्रतिनिधित्व नहीं है।
(vi) समान्तर माध्य की गणना रेखाचित्र से नहीं की जा सकती।
(vii) खुले सिरे वाली समंक श्रेणियों में समान्तर माध्य ज्ञात नहीं किया जा सकता।
(viii) समान्तर माध्य से श्रेणी की रचना के बारे में कुछ पता नहीं चलता।
(ix) अनुपात दर प्रतिशत आदि का अध्ययन करने के लिए यह माध्य सर्वथा अनुपयुक्त है।
(x) कई बार समान्तर माध्य से आश्चर्यजनक व अनुचित निष्कर्ष निकलते हैं। जैसे एक अस्पताल में दाखिल हुए मरीजों की संख्या 18.7 प्रतिदिन ।
प्रश्न 11. माध्यिका से क्या अभिप्राय है ? जब अविच्छन्न श्रेणी दी गई हो तो माध्यिका की गणना किस प्रकार की जाती है?
(What do you mean by median? How is median calculated when a continuous series is given ?)
उत्तर-माध्यिका (Median)-माध्यिका तथ्यों के समूह का वह चर मूल्य है जो समूह को दो बार बराबर भागों में इस प्रकार बाँटता है कि एक भाग में सारे मूल्य माध्यिका से अधिक और दूसरे भाग में सार मूल्य उससे कम हो । डॉ. बाउले के अनुसार, “यदि एक समूह के पदों को उनक मूल्यों के अनुसार क्रमबद्ध किया जाए तो लगभग बीच के पद के मूल्य को माध्यिका कहा जाता है।” मान लें 5 छात्रों के अंक 20, 22, 25, 30 और 32 हैं तो माध्यिका 30 होगी। माध्यिका एक स्थिति वाला माप है।
माध्यिका की गणना (Calculating of Median)- माध्यिका की गणना में निम्नलिखित चरण निहित है-
(i) अंकों को आरोही या अवरोही क्रम में व्यवस्थित किया जाता है।
(ii) उसके बाद संचयी आवृत्ति ज्ञात की जाती है ।
(iii) उसके बाद निम्नलिखित सूत्र का प्रयोग करके केन्द्रीय पद ज्ञात किया जाता है।
(iv) M= आकार (N/2)वीं मद
(v) इसके बाद उस वर्ग को निर्धारित किया जाता है जिसमें मध्यिका स्थित है
(vi) मध्यिका वर्ग ज्ञात हो जाने पर माध्यिका का मूल्य ज्ञात करने के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है-
M=L+N/2-c.f/F×C
प्रश्न 12. माध्यिका के गुण तथा दोष लिखिए।
(Write down the merits and demerits of median.)
उत्तर-माध्यिका के गुण (Merits of median)-माध्यिका के गुण निम्नलिखित हैं-
(i) इसको समझना तथा मूल्य ज्ञात करना सरल है।
(ii) कुछ अज्ञात मूल्यों की अवस्था में भी माध्यिका का मूल्य ज्ञात किया जा सकता है।
(iii) इसे कठोरता सं वर्णित किया जाता है।
(iv) खुले सिर वाले वर्ग के वितरण में भी यह विशेष उपयोगिता है, क्योंकि इसमें कोई कल्पना नहीं करनी पड़ती।
(v) इसका मूल्य रेखाचित्र विधि द्वारा भी ज्ञात किया जा सकता है।
(vi) गुणात्मक तथ्यों जैसे-बुद्धिमता, कार्य-कुशलता, ईमानदारी, दरिद्रता आदि को ज्ञात करने के लिए माध्यिका को सर्वोत्तम माना जाता है।
(vi) यह अपिकिरण तथा विषमता के मापन में भी लाभदायक है।
(vii) यह स्थिति माप है।
(ix) यह श्रेणी के माध्य मूल्य की व्याख्या करता
दोष (Demerits)-माध्यिका के निम्नलिखित दोष हैं-
(i) यह सभी मदों पर आधारित नहीं है।
(ii) मका बीजगणितीय प्रयोग नहीं हो सकता।
(iii) यह निदर्शन में परिवर्तन से प्रभावित होता है अर्थात्
MxN≠£X1+X2+X3+…Xñ
(iv) यह टीक है कि यह चरम मूल्यों से प्रभावित नहीं हाता, परन्तु जहाँ इन मूल्यों का महत्व देना होता है वहाँ यह माध्य अनुपयुक्त है।
(v) यदि एक श्रेणी में मदों का मूल्य समान नहीं है तो भी माध्यिका को ज्ञात नहीं किया जा सकता।
(vi) यदि मदों का मूल्य बहुत कम या अधिक हा तो माध्यिका का ज्ञात करना कठिन हो जाना है।
(vii) अखण्डित श्रेणी में माध्यिका ज्ञात करने के लिये सूत्र द्वारा मध्यिका वर्ग का निर्धारण करना पड़ता है । अत: यहाँ तक कल्पना की जाती है कि आवृत्तियाँ अपने से सम्बन्धित वर्ग में समान रूप से वितरित हैं, परन्तु ऐसा मानना गलत है।
प्रश्न 13.निम्नलिखित दशाओं की गणना कैसे की जाती है ?
(i) जब समावेश श्रेणी हो।
(ii) जब वर्गान्तर असमान हो।
(iii) जब विन्दु रेखीय विधि अपनानी हो।
How will you calculate median in the following cases-
(i) When there is inclusive series.
(ii) When there is unequal class intervals.
(iii) Line graphic method is to be adopted.
उत्तर-पहली स्थिति (First Case)-(i) जब माध्यिका मूल्य ज्ञात करने के लिए समावेशी आवृत्ति वितरण दिया हुआ है तो उसे सर्वप्रथम अपवर्जी श्रेणी में परिवर्तित किया जाता है।
(ii) फिर संचयी आवृत्तियाँ ज्ञात की जाती हैं।
(iii) उसके बाद निम्नलिखित सूत्र का प्रयोग करके केन्द्रीय पद ज्ञात किया जाता है ।
M = size of(N/2) th item
(iv) इसके बाद उस वर्ग को निर्धारित करते हैं जिसमें माध्यिका स्थित है।
(iv) माध्यिका वर्ग ज्ञात हो जाने पर निम्नलिखित सूत्र का प्रयोग किया जाता है-
M=1+N2/2-C/f×C
2. दूसरी सिथति (Second Case)- यदि समंक श्रेणी में वर्ग असमान है तो उसे समान वर्गान्तर बनाने की आवश्यकता नहीं । ऐसी अवस्था में माध्यिका मूल्य ज्ञात करने के लिए समान सूत्र का प्रयोग किया जा सकता है । यदि आवृनियों को समायोजित किया जाता है तब भी माध्यिका में काई अन्तर नहीं आयेगा।
3. तृतीय स्थिति (Third Case)- इसमें निम्नलिखित चरण निहित हैं-
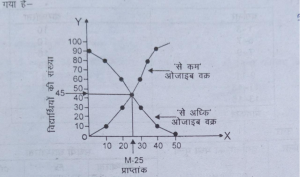
(i) सर्वप्रथम बिन्दु रेखीय पत्र (Graph paper) पर ‘से कम’ तथा ‘से अधिक’ संचयी आजाइव वक्र खींचे।
(ii) जहाँ ये दाना वक्र आपस में काट रस बिन्दु से भुजाक्ष पर लम्ब डालिए ।
(iii) लम्ब भुजाक्ष को जिस बिन्दु पर छुए वही माध्यिका मूल्य होगा। जैसे नीचे चित्र में दिखाया गया है-
प्रश्न 14. बहुलक किसे कहते हैं ? उसके गुणा और दोष बताइए।
(What is Mode ? State its merits and demerits.)
उत्तर-बहुलक एक विशेष प्रकार का माध्य (Average) है । श्रेणी में जिस मद की सबसे अधिक आवृत्ति हो उसे बहुलक (Mode) कहा जाता है। उदाहरण लेकर हम बहुलक अवधारणा का स्पष्टीकरण करते हैं। नीचे श्रमिकों का मासिक वेतन दिया है। इसमें 1600 रुपए मासिक वेतन पाने वाले श्रमिकों की संख्या 26 अर्थात् सबसे अधिक है । अत: बहुलक 1600 रुपये है।
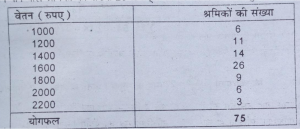
यदि किसी श्रेणी में दो भूयिष्ठक पाए जाएँ तो उसे Bi-Modal Series कहते हैं। भूयिष्ट को जोड़ से सम्बोधित किया जाता है ।
बहुलक के गुण (Merits of Mode) –
(i) यह समझने में सरल है और अधिकांश श्रेणियों में इसका ज्ञान निरीक्षण द्वारा ही प्राप्त किया जा सकता है।
(ii) इसका प्रयोग मुख्यत: उत्पादन और बिक्री के क्षेत्र में किया जाता है।
(iii) इस पर चरम सीमा मूल्यों का प्रभाव नहीं पड़ता ।
(iv) इसकी गणना बिन्दुरेखीय विधि से भी की जा सकती है
बहुलक के दोष (Demerits of Mode)-
(i) यह श्रेणी के सभी पदों पर आधारित होता है ।
(ii) यह अनश्चित और अस्पष्ट होता है ।
(iii) जब श्रणी में एक से अधिक भूयिष्ठक ‘होते हैं तो गणना में कठिनाई होती है।
प्रश्न 15. निम्न बारम्बारता वितरण से समान्तर माध्य, माध्यिका तथा भूयिष्ठक ज्ञात करें।
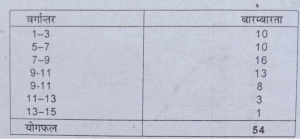
उत्तर-

X=£fx/£f=(376/54)6.96
मध्यिका= N/2 मद का मूल्य= 54/2= 27 मद का मूल्य । अत: मध्यिका 5-7 वर्गान्तर में है।
मध्यिका= 1¹+N2/2-C/f×1= 5+(27-13/16)×2 = 5+(14/16)×2 = 5+(7/4)= 5+1.75= 6.75
भूयिष्ठक (बहुलक ) की गणना-
16 सबसे अधिक बारम्बारता है, अतः मॉडल वर्ग 5-7 है।
अतः भूयिष्ठक= 1+fo-f1\2fo-f1-f2×h
=5+(16-10/32-10-13)×2
=5+6/9×2 = 5+1.33= 6.33
अतः मध्यिका 6.75 माध्य तथा भूयिष्ठक के बीच में है।
प्रश्न 15.45 और 55 का कल्पित माध्य लेते हुए ज्ञात कीजिए और पुष्टि कीजिए कि दोनों स्थितियों में परिणाम एक ही है।

उत्तर-45 कल्पित माध्य लेते हुए माध्य की गणना (Calculation of mean taking 45 as assumed mean)-
कल्पित माध्य (AM) =45
X= AM+£fd/N×10
=45+135/100×10
= 43 + 13.5 = 58.5
प्रश्न 16. कल्पत माध्य लेते हुए माध्य की गणना
(Calculation of mean taking 55 as assumed mean.)
कल्पित माध्य (AM) = 55
X = AM+ £fd/N×10 = 55+35/100 x10
= 55 +3.5 = 58.5
प्रश्न 17.20 विद्यार्थियों के औसत अंक 50 हैं जिनका विवरण निम्न प्रकार से है।
स्याही के फैल जाने से एक अंक पढ़ा नहीं जा सकता। इसे ज्ञात कीजिए।
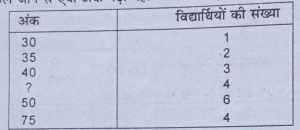
उत्तर – हम मान लेते हैं कि अज्ञात अंक x है।
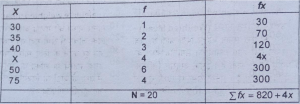
X=Σfx/N
अथवा = 820+4x/20
अथवा, 820 + 4x = 1000;
4x = 1000-820 = 180
180
x = x 180/4= 45
अतः अज्ञात अंक = 45
प्रश्न 18. 25.000, 31.40, 28,00, 24.00,26.50, 34.00, 35.00, 23.70, 30 25,33.00, 38.60, 28,00, 28.00, 30.00, 30.50, 34.00, 29.00, 23.00, 27.20, 22.50,32.20.
ऊपर दिए गए अंकों की सहायता से सिद्ध करें कि मध्यिका का मूल्य समान्तर माध्य भूयिष्ठक के बीच में है।
उत्तर –
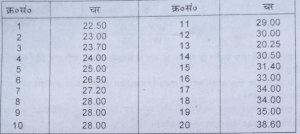
(i) x=£x\n =583.85\20 = 29.1925
(ii) मध्यिका= n+1/2 वीं मद = 20+1/2 =10.5 मद
=20.00 +29.00/2 = 28.50
(iii) भूयिष्ठक = 28 (28 की बारम्बारता सबसे अधिक है।)
अत: माध्यिका मूल्य (28.5), समान्तर माध्य (29.125), तथा भूयिष्ठक (28) के बीच में है।
प्रश्न 19. भारित माध्य क्या है ? एक उदाहरण देकर भारित माध्य की गणना समझाइए।
(What is weighted mean? Illustrate how to calculate weighted mean.)
उत्तर-भारित माध्य (Weithted Mean)-सरल समान्तर माध्य की गणना करते समय सभी पदों को एक समान महत्त्व दिया जाता है, जबकि वास्तविक जीवन में सभी मदों का महत्त्व एक समान नहीं होता। साधारण समान्तर माध्य के इस दोष को दूर करने के लिए भारित माध्य का प्रयोग किया जाता है। इसके अनुसार विभिन्न मदों को उनके महत्त्व या शक्ति के अनुसार भार दे दिया जाता है । भारित समान्तर माध्य सूचकांक बनाने में तथा दो बोर्डों या विश्वविद्यालयों के परिणामों की तुलना करने में प्रयोग किया जाता है। इसका सूत्र निम्नलिखित है-
XW=ΣWX/ΣW
जहाँ XW = भारित माध्य (Weighted Mean)
ΣWX= चारों ओर भारों के गुणनफल का योग
ΣX= भारों का योग
उदाहरण-

ΣW=ΣWX/ΣW= 690/20= 34.5
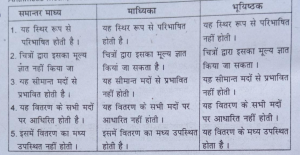
प्रश्न 20. केन्द्रीय प्रवृत्ति के मापक के रूप में समान्तर माध्य, माध्यिका और भूयिष्ठक के भेद करें।
(Compare the arithmetic mean, median and mode as measure of central tendancy.)
उत्तर-समान्तर माध्य, माध्यिका और भूयिष्ठक में तुलना (Comparison among Arithmetic mean, Median and mode)-
प्रश्न 21. कुछ परिवारों का दैनिक व्यय रुपयों में दिया गया है-

(i) माध्य, माध्यिका तथा बहुलक ज्ञात करें ।
(ii) उच्चतम चतुर्थक तथा निम्नतम चतुर्थक ज्ञात करें।
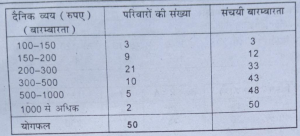
माध्यिका= N/2,मद का मूल्य=50/2= 25 वें मद जो 200-300 वर्गान्तर में है।
अत: माध्यिका = 1+{(n/2-c.f)/f}×1 =200(25-12/21)×100
=200+(13/21)×100. =200+61.9= 261.90
निम्नतम चतुर्थक (Q1) =n/4=50/4=12.5 मद का मूल्य अर्थात् चतुर्थांक 200-300 वर्गान्तर में है।
अत:. Q1 = 1+n/4-c.f/f×1 =200+12.5-12/21×100
200+ 0.5/21 x100 = 200+0.5/21 x 100 = 200 +2.38 = 202.38
उच्चतम चतुर्थक (Q4) =3n/4=150\4 = 37.5 वें मद का मूल्य जो 300-500 वर्गान्तरों में है।
अत: Q3 = 1¹+3m/4-c.f/f×1 =300+37.5-33/10×200
= 300+4.5/10 x 200 = 300 +90 = 390
बहुलक (Z) = 200+21-9/23 x 100 = 200 + 52.17 = 252.17
समान्तर माध्य =भूयिष्ठक = 3 (समान्तर माध्य- माध्यिका)
अथवा x =3m-z\2= (3 x 261.90)-252.17/2
=785.70-252.17/2
= 266.765
प्रश्न 22. निम्नलिखित आवृत्ति वितरण से समान्तर माध्य (Arithmetic Mean) तथा मध्यिका (Median) ज्ञात कीजिए-
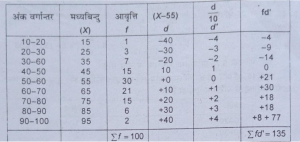
उत्तर-
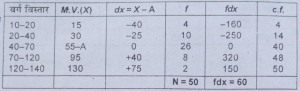
X= A+£fdx/N =55+60\50=56.2
अत: x = 56.2
M= आकार (50/3) वीं मद
= आकार (50/2) वीं मद
= 25वीं मद का आकार
25वीं मद वर्ग 40-70 में स्थित है। यही मध्यम वर्ग होगा।
सूत्र के अनुसार
M=1¹+ (N/2-c.f)/f×i
=40+25-14/26×30
=40+11/26×30 =52.69
अत:x= 56.2M= 52.69
प्रश्न 23.50 विद्यार्थियों के औसत अंक 44.8 हैं, जिनका विवरण नीचे दिया गया है-
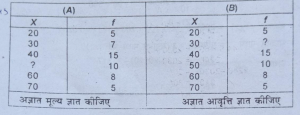
उत्तर-(A) अज्ञात मूल्य का निर्धारण (Location of Unknown Value)-
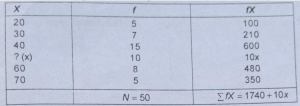
अब हम इस सूत्र का प्रयोग करते हैं-
X =ΣfX\N
अज्ञात मूल्य का प्रयोग करने के लिए-
44.8 = 1740+10x/50
44.8×50 = 1740+ 10x
2240 – 1740= 10x
500 = 10x
50 =X
अत: अज्ञात मूल्य 50 है।
उत्तर-(B) अज्ञात आवृत्ति का निर्धारण (Location of Unknown Value)-
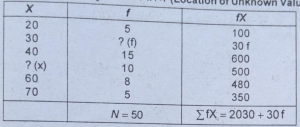
अब हम इस सूत्र का प्रयोग करते हैं-
X=ΣfΧ/N
44.8= 1740+10x/50
44.8 x 50 =2030+30f
2240 = 2030 + 30f
2240 -2030 = 30f
210= 30f
7 = 1
अत: अज्ञात आवृत्ति 7 है।
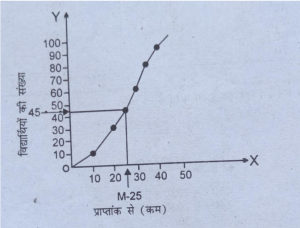
प्रश्न 24. निम्नलिखित आँकड़ों से बिन्दु रेखीय विधि (से कम ओजाइब ) से माध्यिका मूल्य ज्ञात करें-

उत्तर-

(i) माध्यिका की गणना करने के लिए बिन्दु रेखाय पत्र (Graph Paper) पर क्रम से संचयी ओजाइब वक्र खींचें।
(ii) N/2की गणना करने के लिए 50 को 2 से भाग करें। भजनफल 25 आएगा । y अथा पर 25 अंकित करेंगे।
(iii) इसके बाद अंकित बिन्दु से ओजाइव वक्र पर लम्ब गिराएँगे। यह लम्ब भुजाक्ष पर जिस मूल्य पर छूता है, वही माध्य का मूल्य होगा। नीचे चित्र से पता चलता है कि लम्ब भुजाक्ष पर 20 पर छूता है। अत: माध्यिका 20 होगी।
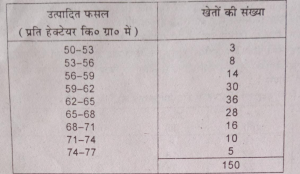
प्रश्न 25. निम्न सारणी में किसी गाँव के 150 खेतों में गेहूँ की प्रति हेक्टेयर पैदावार की गई है । उत्पादित फसलों का समांतर माध्य, माध्यिका तथा बहुलक परिकल्पित कीजिए।
उत्तर-माध्य तथा माध्यिका की गणना
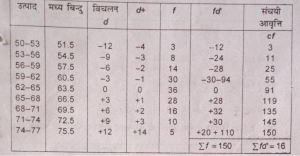
A.M.=63.5
C =3
माध्यिका (X) = A.M.+£fd/£f xC=63.5+16/150×3
= 63.5+48/150
= 63.5+0.32 =63.82 उत्तर
माध्यिका (Median) = N/2 मद का मूल्य =150/2= 7.5
75 वें मद का मूल्य 62-65 वर्गान्तर में है।
अत: माध्यिका (Median) = 1¹+N/2-c.f/f×C= 62+75-55/36×3
= 62+ 20/36×3 =62+20/12=62+1.67=63.67उत्तर
बहुलक की गणना- विद्यार्थी स्वयं ज्ञात करें। उत्तर-63.29 कि. ग्राम प्रति हेक्टेयर ।
प्रश्न 26. एक उदाहरण से सिद्ध करें कि यदि (i) एक श्रेणी के विभिन्न मदों में 2 जोड़े जाएँ तो समान्तर माध्य में 2 की वृद्धि हो जाएगी।
(i) एक श्रेणी के विभिन्न मदों में 2 घटाये जाएँ तो समान्तर माध्य 2 कम होगा ।
(ii) एक श्रेणी के विभिन्न मदों को दो से गुणा किया जाए तो समान्तर माध्य दोगुना होगा ।
(iii) एक श्रेणी के विभिन्न मदों को दो से विभाजित किया जाए तो समांतर माध्य आधा हो जाएगा।
उत्तर-निम्न उदाहरण से प्रश्नों में दिए गए कथनों की पुष्टि होती है।
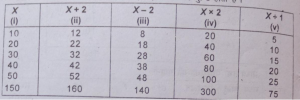
कॉलम (i) X =150/5= 30
कॉलम (ii) X=160/5=32(30+2)
कॉलम (iii)X=140/5=28(30-2)
कॉलम (iv)X= 75/5=15(30÷2)
प्रश्न 27. निम्न वितरण में लुप्त आवृत्तियों को बताएँ यदि विद्यार्थियों की संख्या 100 तथा माध्यिका 30 हो।

उत्तर-मान लें एक लुप्त आवृत्ति =f1
दूसरी लुप्त आवृत्ति = f2
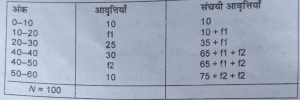
हम जानते हैं कि अंतिम वर्गान्तर का संचयी आवृत्ति आवृत्तियों के योगफल के बराबर होती है।
अत: 75 +f1+f2 = 100
f1+f2 = 100 – 75 = 25
अब माध्यिका =1¹+N/2-c.f/f×i = 30+50(35-f1)/30×10
अथवा, 30 = 20+50-35-f1/30
अथवा,0/1= 15-f1/3
अथवा, 0= 15- f1
अथवा,f1 = 15
(i) समीकरण में f1 का मूल्य रखने पर
15 + f2 = 25
f1= 25 – 15 = 10
प्रश्न 28. निम्न श्रेणी से माध्यिका ज्ञात करें-
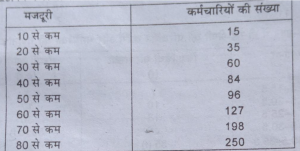
उत्तर-सर्वप्रथम हम संचयी आवृत्तियों को साधारण वितरण में परिवर्तित करेंगे तब माध्यिका की गणना करेंगे।
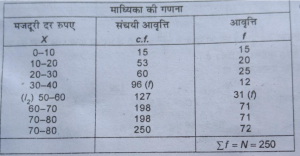
माध्यिका =(N/2) वें मद का मूल्य
250/2 = 125 वमें मद का मूल्य जो 50-60 वर्गान्तर में निहित है।
माध्यिका = 11+1¹+ N/2-c.f/f×C
= 50+125 – 96/31×10
50+29/11×10 =59.35 उत्तर
प्रश्न 29. निम्नलिखित आँकड़ों की सहायता से माध्यिका ज्ञात करें-

उत्तर-प्रश्न में दी गई श्रेणी को परिवर्तित करेंगे और माध्यिका की गणना करेंगे।
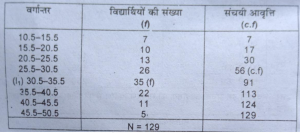
माध्यिका =(N/2) वें मद का मूल्य = 129/2= 64.5 वें मद का मूल्य । 64.5 मद का मूल्य 30.5-35.5 वर्गान्तर में स्थित है।
सूत्र का प्रयोग करने पर
माध्यिका =1² +N/2-c.f/f×C
= 30.5+129/2-56/35×5
=30.5+64.5-55/35×5
=30.5+8.5/7 =31.7 अंक
प्रश्न 30. निम्नलिखित तालिका से ग्राफ की सहायता से बहुलक ज्ञात करें तथा गणित का सहायता से परिणाम की जाँच करें।
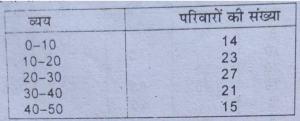
रेखीय चित्र द्वारा बहुलक की गणना
(Calculation of Mode Graphically)
सूत्र द्वारा परिणाम की जाँच-निरीक्षण से पता चलता है कि बहुलक वर्ग 20-30 है।
प्रश्न 31. निम्नलिखित तालिका से बहुलक की गणना करें।
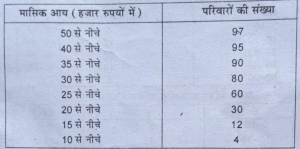
उत्तर-प्रश्न में संचयी बारम्बारता वितरण है । बहुलक को गणना करने के लिए हमें इसे अपवर्ती श्रृंखला में बदलना होगा। प्रश्न में शृंखला अवरोही क्रम में निरीक्षण करने पर हमें पता चलता है कि बहुलक का मान 25-30 वर्गान्तर है। अब हम समूह सारणी तथा विश्लेषण सारणों बनाएंगे।
समूहन सारणी

विश्लेषण सारणी
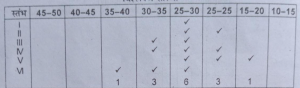
अब। L=25
D¹=(30-18)12;D²=(30-20)=10
h=5
अब सूत्र का प्रयोग करते हुए बहुलक की गणना की जा सकती है।
m=D1/D1+D×h
=25+12/10+12×5
=27.273 रुपए
प्रश्न 32. उदाहरण देकर सिद्ध करें कि यदि समंक श्रेणी में वर्ग अंतराल असमान है तब वर्गान्तर बनाए बिना भी मध्यिका एक जैसी आएगी।
उत्तर-यह सिद्ध करने के लिए कि समंक श्रेणी में वर्ग अन्तराल को समायोजित करें या न करें, तब भी माध्यिका एक जैसी आयेगी । हम नीचे एक काल्पनिक तालिका लेते हैं।
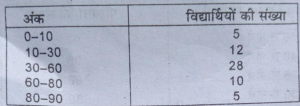
असमायोजित वर्गान्तर से माध्यिका की गणना

माध्यिका =N/2 मद का मूल्य=60/2= 30 वें मद का मूल्य
30वें मद का मूल्य 30-60 के वर्ग में आता है।
अत: माध्यिका = 1+n/2-c.f/f×1 =30+30-17/28×30
=30+13/28×30=30+13.9=43.9
अब हम सें श्रेणी को समान वर्गअन्तराल में परिवर्तित करेंगे-

माध्यिका=N/2मद का मूल्य=60/2 = 30 वें मद जो 30-60 के वर्ग में आता है।
अत: माध्यिका =1+n/2-c.f/f×1
=30+30-17/28×10
=30+13/28×30
=30+13.9=43.9
इस प्रकार हम देखते हैं कि दोनों विधियों से माध्यिका एक समान है।
प्रश्न 33. रेखाचित्र द्वारा निम्नलिखित आवृत्ति वितरण में भूयिष्ठक का मूल्य ज्ञात कीजिए और गणितीय विधि से मूल्य की जाँच कीजिए-

उत्तर-पहले हमें श्रृंखला से आवृत्ति आयत चित्र (Histogram) बनाना होगा। फिर नीचे प्रदर्शित उदाहरण की भाँति सबसे बड़े आयत के बिन्दुओं को आस-पास के आयत बिन्दुओं से मिलाकर भूयिष्ठक ज्ञात कर लिया जाएगा।
बीजगणितीय विधि द्वारा मूल्य की जाँच :
Z=1¹+f¹-fo/2f¹-fo-f²×1 या, (1²-1¹)=20+15-10/30-10-5×10
=20+50/15=23.3

प्रश्न 34. एक परीक्षा में 100 अभ्यार्थी थे, जिनमें 21 अनुत्तीर्ण हुए, 6 को विशिष्टता प्राप्त हुई, 43 तृतीय श्रेणी में तथा 18 द्वितीय श्रेणी में उत्तीर्ण हुए। विशिष्टता प्राप्त करने के लिए 75% अंक चाहिए, कम-से-कम 40% उत्तीर्णता के लिए, द्वितीय श्रेणी में उत्तीर्ण के लिए कम-से-कम 50% तथा प्रथम श्रेणी के लिये कम-से-कम 60% अंक चाहिये । अंकों के वितरण के लिए माध्यिका की गणना करें।
उत्तर – (i) कुल छात्र = 100
(ii) अनुत्तीर्ण छात्र = 21
(iii) उत्तीर्ण = 100-21 =79
(iv) विशिष्टता प्राप्त करने वाले अभ्यार्थी = 6
(v) तृतीय श्रेणी में पास होने वाले अभ्यार्थी = 43
(vi) द्वितीय श्रेणी में पास होने वाले अभ्यार्थी = 6
(vii) 60% से अधिक अंक प्राप्त करन वाले अभ्यार्थी
= 79-(43 +43) = 79 – 61 = 18
(viii) विशिष्टता प्राप्त करने वाले अभ्यार्थी = 6
(ix) 60 से ऊपर तथा 75 सें कम अंक प्राप्त करने वाले अभ्यार्थी = 18-6 = 12 इन आँकड़ों को हम निम्न आवृत्ति वितरण में दिखा सकते हैं-
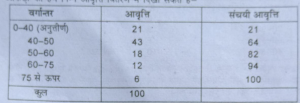
माध्यिका=7/2 मद का मूल्य
100/2 अर्थात् 50वें मद का मूल्य
अतः माध्यिका 40-50 वर्गान्तर में है।
माध्यिका =1+n/2-c.f/f×1
=40+100/2-21/43×10
=40+50-21/43×10
=40+29/43×10=40+290/43 = 430+6.47=46.47
प्रश्न 35. आपको 5 मदों के मूल्य दिए गए हैं-4, 6, 8, 10 तथा 12.
(i) यदि उनका माध्य 2 से बढ़ा दिया जाए तो व्यक्तिगत मदों में क्या परिवर्तन होगा यदि सभी मद समान रूप से प्रभावित होते हैं।
(ii) यदि पहले तीन मदों के मूल्य में दो की वृद्धि होती है, तब बाद के दो मदों का मान क्या होना चाहिए ताकि माध्य पूर्ववत् बना रहे ।
(iii) यदि मान 12 के स्थान पर 96 का प्रयोग करें तब समान्तर माध्य क्या होगा?
उत्तर-(i) 4+6+8+10 +12 /5= 40/5 = 8
नया नाम = 8+2= 10
मान लो प्रत्येक मद में बढ़ोतरी= X
नई मदों का मूल्य= 4+x+6+x+8+x+10+x+12+x
=40+5x
अतः
40 + 5x = 10 x 5
5x=50-40 = 10
x=2
अत: बाद के दो मदों में 2 की वृद्धि होगी।
(ii) तीन मदों के मूल्य में कुल वृद्धि = 3 x 26
अतः बाद के दो मदों के मूल्य में कमी =6
औसत वृद्धि=6/2= 3
अत: बाद के दो मदों में 3.3 की वृद्धि होगी।
पुष्टिकरण (Verification) :5 मदों के मूल्य का माध्य = 8
मदों के परिवर्तन के पश्चात् मदों के मूल्य का माध्य
= (4+2 +6+2 + 8 + 2 + 10-3+ 12-3) + 5
=6-8-10-7-9/5=40\5=8
(3) पाँचव मद के मूल्य में काफी परिवर्तन आएगा। इससे स्पष्ट होता है कि समान्तर माध्य चरम सीमा से काफी प्रभावित होता है।
वस्तुनिष्ठ प्रश्न
(Objective Type Questions)
प्रश्न 1. बताइए कि निम्नलिखित कथन सही है या गलत-
(क) माध्यिका से मदों के विचलनों का योग शून्य होता है।
(ख) श्रृंखलाओं की तुलना के लिए मात्र औसत ही पर्याप्त नहीं है।
(ग) समांतर माध्य एक स्थैतिक मूल्य
(घ) उच्च चतुर्थक शीर्ष 25 प्रतिशत मदों का निम्नतम मान है।
(ङ) माध्यिका चमर प्रेक्षणों द्वारा अनुचित रूप से प्रभावित होती है।
उत्तर-(क) गलत
(ख) सही
(ग) गलत
(घ) सही
(ङ) गलत।
प्रश्न 2. प्रत्येक प्रश्न के सामने दिए गए बहु विकल्पों में से सर्वाधिक उचित विकल्प को चिह्नित करें-
(i) गुणात्मक मापन के लिए सर्वाधिक उपयुक्त औसत (Average) है।
(क) समांतर माध्य
(ख) माध्यिका
(ग) बहुलक
(घ) ज्यामितीय माध्य
(ङ) उपर्युक्त में से कोई नहीं
(ii) चरम पदों की उपस्थिति से कौन-सा सर्वाधिक प्रभावित होता है-
(क) माध्यिका
(ख) बहुलक
(ग) समांतर माध्य
(घ) ज्यामितीय माध्य
(ङ) हरात्मक माध्य
(iii) समांतर माध्य से मूल्यों के किसी समुच्चय में विचलन का बीजगणितीय योग है।
(क) द
(ख) 0
(ग) उपर्युक्त कोई भी नहीं
उत्तर-(i) ख (ii) ग (iii) ग
प्रश्न 3. निम्नलिखित स्थितियों में कौन-सा औसत उपयुक्त होगा?
(क) तैयार वस्त्रों के औसत आकार ।
(ख) एक क्षिा में छात्रों की औसत बौद्धिक प्रतिभा ।
(ग) एक कारखाने में प्रति पाली औसत उत्पादन ।
(घ) एक कारखाने में औसत मजदूरी ।
(ङ) जब औसत से निरपेक्ष विचलनों का योग न्यूनतम हो ।
(च) जब चरों की मात्रा अनुपात में हो।
(छ) मुक्तांत बारम्बारता बंटन के मामले में।
उत्तर – अध्यापक की सहायता से विद्यार्थी स्वयं करें।
