bihar board class 11 math notes | समुच्चय

4 February 20214 February 2021

प्रमुख तथ्य एवं परिभाषा

समुच्चय (Set)-‘Set’ शब्द बोलचाल की भाषा का बहुत ही प्रचलित शब्द है और सदा इसका अर्थ समूह (collection) से लेते हैं जैसे किताबों का सेट, ताश की गड्डी, टी सेट आदि। गणित में भी set (समुच्चय) का अर्थ समूह से ही होता है। उदाहरण के लिए, एक सरल रेखा बिन्दुओं का समूह है तथा एक तल सरल रेखाओं का समूह है।

रिक्त समुच्चय (Null set) -वह set जिसमें कोई भी element नहीं हो, उसे null set (रिक्त समुच्चय) कहते हैं। null set को चिह्न से सूचित किया जाता है।

परिमित एवं अपरिमित समुच्चय (Finite and infinite set)-वह set जिसमें elements की संख्या परिमित (finite) हो अर्थात् वह set जिसके elements के बारे में यह कहा जा सकता है कि वह पहला element है, वह दूसरा element है, वह तीसरा element है, इत्यादि, अर्थात् दूसरे शब्दों में वह set जिसके elements को natural numbers के set (1, 2, 3, … n) के साथ, किसी n के लिए, एक-एक अनुरूपता (one-to-one correspondence) में रखा जा सकता है, उसे finite set कहा जाता है। वह set जिसमें elements की संख्या infinite हो अर्थात् वह set जिसमें elements की संख्या finite नहीं हो, उसे infinite set कहा जाता है।

उपसमुच्चय (Subset and Superset)-यदि A और B दो sets हों इस प्रकार से कि A का हरेक element, B का भी element है तो हम कह सकते हैं कि A, B का subset

है।

Proper Subset -यदि A और B दो sets ऐसे हों कि A का हरेक element B का भी एक element है और B में कम-से-कम एक ऐसा element है जो A में नहीं है तो हम कहते हैं कि A, B का एक proper subset है और इसे AC B के रूप में लिखतें हैं।

शक्ति समुच्चय (Power Set)—वह set जो किसी set A के सभी सम्भव subsets की समष्टि (collection) है set A का power set कहलाता है। set A के power set को P(A) से [या 2A से] सूचित किया जाता है।

सार्वत्रिक समुच्चय (Universal Set) – set theory में हमने विभिन्न sets पर विचार . किया है जो सम्भवतः किसी (fixed) निश्चित set के subset होंगे।

अतः उस निश्चित set को, जिसके सभी विचाराधीन sets subsets होते हैं, universalset कहा जाता है अर्थात् universalset एक ऐसा निश्चित set है जो विचाराधीन sets के elements की एक समष्टि (totality) है।

Universal set को साधारणतः अक्षर 2 से सूचित किया जाता है।

Union का व्यापक रूप : हमलोग ऊपर दो sets के union के बारे में पढ़ चुके हैं। लेकिन इस परिभाषा से किसी भी संख्या के sets का union मालूम किया जा सकता है। मान लिया कि S, SS, कोई तीन sets है। तो तीनों sets का union उन सब elements

X का एक set होगा जो S1 S2 S3 में से कम-से-कम एक में होगा और हम उस union को, पहले के अनुसार इस प्रकार लिखते हैं : S1, U S2,U S3.

सर्वनिष्ट (Union)-मान लिया कि A और B दो sets हैं। तो A और B sets का. intersection उन सभी points x का set है जो दोनों A और B sets में शामिल है अर्थात् X ϵ A और x ϵ B. A और B के intersection को A ∩ B से सूचित किया जाता है।

Intersection का व्यापक रूप-Sets के union की तरह, यहाँ भी हम दो से अधिक sets के intersection पर विचार कर सकते हैं। मान लिया कि SI, S2, S3, तीन sets हैं। तो SI, S2,S3 तीनों sets का intersection वह एक set होगा जो उन सब elements x से बना है जो तीनों sets में उभयनिष्ठ (common) हैं।

S1, S2, S3, के intersection को हम S1 ∩ S2 ∩S3 से व्यक्त करते हैं।

असंयुक्त समुच्चय (Disjoint Sets)-मान लिया कि A और B दो sets हैं। तब sets A और B को disjoint (असंयुक्त) कहा जाता है यदि कोई भी elements उन दोनों में उभयनिष्ठ नहीं हों अर्थात् यदि उन दोनों sets का intersection शून्य हो।

Idempotent Laws:

(a) A U A = A

(b) A ∩ A = A

तत्समक नियम (Identity Laws)

(a) A U ϕ = A

(b) A ∩ ϕ = ϕ

(a) A U Ώ = Ώ

(b) A ∩ Ώ = A

क्रम-विनिमेय नियम (Commutative Laws)

(a) A U B = B U A

(b) A ∩ B = B ∩ A

साहचर्य नियम (Associative Laws)

(a) (A U B) U C = A U (B U C)

(b) (A ∩ B) ∩ C = A ∩ (B ∩ C)

बंटन नियम (Distributive Laws)

(a)A U (B ∩ C)= (A U B) ∩ (A U C)

(b) A ∩ (B U C)= (A ∩ B) U (A ∩ C)

पूरक नियम (Complemen)t Laws)

(a) A U A’ = Ώ

(b) A ∩ A’ = ϕ

8.(a) (A) = A

(b) Ώ = ϕ, ϕ = Ώ

9.(a) (A U B) = A ∩ B’

(b)(A ∩ B) = A U B’

(a) A – (B U C)= (A – B) ∩ (A – C)

(b)A – (B ∩ C)= (A – B) U (A – C)

(a)A – B = A ∩ B’

(b) A – B = B’ – A’

प्रश्नावली 1.1

निम्नलिखित में कौन से समुच्चय हैं? अपने उत्तर का औचित्य बताइए।

(i)J अक्षर से प्रारंभ होने वाले वर्ष के सभी महीनों का संग्रह।

(ii) भारत के दस सबसे अधिक प्रतिभाशाली लेखकों का संग्रह।

(iii) विश्व के सर्वश्रेष्ठ ग्यारह बल्लबाजों का संग्रह।

(iv) आप की कक्षा के सभी बालकों का संग्रह।

(v) 100 से कम सभी प्राकृत संख्याओं का संग्रह।

(vi) लेखक प्रेमचन्द द्वारा लिखित उपन्यासों का संग्रह।

(vii) सभी सम पूर्णाकों का संग्रह।

(viii) इस अध्याय में आने वाले प्रश्नों का संग्रह।

(ix) विश्व में सबसे अधिक खतरनाक जानवरों का संग्रह।

हल :

(i) Jसे शुरु होने वाले महीनों के नाम: जनवरी, जून व जुलाई। यह एक समुच्चय है।

(ii) प्रतिभाशाली लेखक को परिभाषित नहीं किया जा सकता .: यह एक समुच्चय

नहीं है।

(iii) सर्वश्रेष्ठ बल्लेबाज को परिभाषित नहीं कर सकते। यह एक समुच्चय नहीं है।

(iv) हमारी कक्षा के विद्यार्थी ज्ञात है। परिभाषित है। यह एक समुच्चय है।

(v) 100 से कम प्राकृत संख्याएँ 1, 2, 3, …, 99 हैं। यह एक समुच्च है।

(vi) लेखक प्रेमचनद द्वारा लिखित उपन्यासों का संग्रह परिभाषित है। यह एक __समुच्चय है।

(vii) समपूर्णांक { …., -4,-2, 0, 2, 4, 6, …} है। यह एक समुच्चय है।

(viii) इस अध्याय के प्रश्न परिभाषित है यह एक समुच्चय है।

(ix) संसार के सबसे अधिक खतरनाक पशुओं का संग्रह को परिभाषित नहीं किया

जा सकता। यह एक समुच्चय नहीं है।

मान लीजिए A = {1,2,3,4, 5, 6} रिक्त स्थानों में उपयुक्त प्रतीक ८ अथवा !

भरिए

(i) 5…A (ii) 8…A (iii) 0…A (iv) 4…A (v) 2…A (vi) 10…A

हल : (i)5 ϵ A (ii) 8 ϵ A (iii) 0 ϵ A

(iv)4 ϵ A (v)2 ϵ A (vi) 10 ϵ A

निम्नलिखित समुच्चयों को रोस्टर रूप में लिखिए:

(i) A : {x 😡 एक पूर्णांक है और -3 < x > 7}

(ii) B = {x: x संख्या 6 से कम एक प्राकृत संख्या है।

(iii) C = {x : x दो अंकों की ऐसी प्राकृत संख्या है जिस के अंकों का योगफल 8 है।

(iv) D = {x : x एक अभाज्य संख्या है जो 60 की भाजक है }

(v) E = TRIGONOMETRY शब्द के सभी अक्षरों का समुच्चय है।

(vi) F = BETTER शब्द के सभी अक्षरों का समुच्चय है।

हल :

(i) A = {-2,- 1, 0, 1, 2, 3, 4, 5, 6}

(ii) B = { 1, 2, 3, 4, 5)

(iii) C = { 17, 26, 35, 44, 53, 62,71, 80}

(iv) D = { 2, 3, 5)

(v) E = { T, R, I, G,O, N, M, E, Y} (vi) {B, E, T, R}

निम्नलिखित समुच्चयों को समुच्चय निर्माण रूप में व्यक्त करें

(i) { 3, 6,9,12} (ii) {2, 4, 8, 16, 32} (iii) {5, 25, 125, 625)

(iv) {2, 4, 6, …} (v) {1, 4, 9,… 100}

हल :

(i) A = {x : xएक प्राकृत संख्या है जो 3 से विभाजित होती है और x < 15}

(ii) B = {x : x = 2″, n E N और n < 6}

(iii) C = {x : x 2ⁿ ,n ϵ N तथा n ≤ 4}

(iv) D = {x : x एक सम प्राकृत संख्या है}

(v) E = {x : x = n², n ϵ N और :1 < 11}

निम्नलिखित समुच्चयों के सभी अवयव (सदस्यों) को सूचीबद्ध करें

(i) A = {x 😡 एक विषम प्राकृत संख्या है}

(ii) B= {x: x एक पूर्णांक है, -<<

(iii) C = {x: x एक पूर्णांक है, x² < 4}

(iv). D = {x: x, LOYAL शब्द का एक अक्षर है}

(v) E = {x:x वर्ष का एक ऐसा महीना है जिस में 31 दिन नहीं होते हैं।

(vi) F = {x 😡 अंग्रेजी वर्णमाला का एक व्यंजन है, जो k से पहले आता है।

हल :

(i) A = {1, 3, 5, 7,…}

(ii) B = {0,1, 2, 3,4}

(iii) C = {-2,-1, 0, 1, 2)

(iv) D = { L, O, Y, A}

(v) E = {फरवरी, अप्रैल, जून, सितम्बर, नवम्बर

(vi) F = {b, C, d; f, g, h, j}

बाईं ओर रोस्टर रूप में लिखित और दाईं ओर समुच्चय निर्माण रूप में वर्णित

समुच्चयों का सही मिलान कीजिए:

(i) {1, 2, 3,6} (a) {x 😡 एक अभाज्य संख्या है और 6 की भाजक है।

(ii){2, 3} (b) {x 😡 संख्या 10 से कम एक विषम प्राकृत संख्या

है}

(iii) {M, A, T, H, E, I,C,S} (c) {x:x एक प्राकृत संख्या है और 6 की भाजक है

(iv) {1, 3,5,7,9} (d) {x: x MATHEMATICS pro oht Tato अक्षर है

हल : (i) → (c); (ii) → (a); (iii) → (d); (iv) 7 (b).

प्रश्नावली 1.2

निम्नलिखित में से कौन से रिक्त समुच्चय के उदाहरण है?

(i) 2 से भाज्य विषम प्राकृत संख्याओं का समुच्चय

(ii) सम अभाज्य संख्याओं का समुच्चय

(iii) {x 😡 एक प्राकृत संख्या है, x < 5 और साथ ही साथ x > 7}

(iv) {y: Y किन्हीं भी दो समांतर रेखाओं का उभयनिष्ठ बिन्दु है}

हल :

(i) यह एक रिक्त समुच्चय है।

(ii) सम अभाज्य संख्या का समुच्चय {2} है। यह एक रिक्त समुच्चय नहीं है।

(iii): <5 और 3> 7 कोई प्राकृत संख्या नहीं है यह एक रिक्त समुच्चय है।

(iv) समांतर रेखाएँ कहीं भी मिलती नहीं है। यह एक रिक्त समुच्चय है।

निम्नलिखित समुच्चयों में से कौन से परिमित और कौन से अपरिमित हैं।

(i) वर्ष के महीनों का समुच्चय।

(ii) { 1,2,3,….}

(iii) { 1, 2, 3, ….,99, 100}

(iv) 100 से बड़े घन पूर्णांकों का समुच्चय

(v) 99 से छोटे अभाज्य पूर्णांक का समुच्चय

हल :

(i) वर्ष में 12 महीने होते हैं।

अतएव यह एक परिमित समुच्चय है।

(ii) समुच्चय {1, 2, 3, ….} में अनंत अवयव है।

यह एक अपरिमित समुच्चय है।

(iii) समुच्चय {1, 2, 3,…, 99, 100 में 100 अवयव है।

यह एक परिमित समुच्चय है।

(iv) 100 से अधिक पूर्णांकों का समुच्चय {101, 102, 103, ….} है जिसमें अनंत

अवयव है।

यह एक अपरिमित समुच्चय है।

(v) 99 से कम अभाज्य संख्याओं का समुच्चय 12, 3, 5, 7, …., 97} है जिसमें

अवयवों की संख्या निश्चित है।

यह एक परिमित समुच्चय है।

निम्नलिखित समुच्चयों में से प्रत्येक के लिए बताइए कि कौन परिमित है तथा कौन

अपरिमित है

(i) x – अक्ष के समांतर रेखाओं का समुच्चय

(ii) अंग्रेजी वर्णमाला के अक्षरों का समुच्चय

(iii) उन संख्याओं का समुच्चय जो 5 के गुणज है।

(iv) मूल बिन्दु (0,0) से हो कर जाने वाले वृतों का समुच्चय।

हल :

(i) x-अक्ष के समांतर अनंत रेखाएँ हो सकती हैं।

… यह एक अपरिमित समुच्चय है।

(ii) अंग्रेजी वर्णमाला के 26 अक्षर होते हैं।

इन अक्षरों से बनने वाला समुच्चय परिमित होगा।

(iii) 5 से विभाजित होने वाली संख्याओं का समुच्चय {5, 10, 15, 20, ….} है। जिसमें

अनंत अवयव है।

.. यह एक अपरिमित समुच्चय है।

(v) मूल बिन्दु (0,0) से गुजरने वाले अनन्त वृत बनाए जा सकते हैं।

.. यह एक अपरिमित समुच्चय है।

निम्नलिखित में बताइए कि A = Bहै अथवा नहीं है

(i) A = {a, b, c, d} B = {d, c, b, a}

(ii) A = {4, 8, 12, 16} B = {8, 4, 16, 8}

(iii) A = {2, 4, 6, 8, 10}

B= {xx सम घन पूर्णांक है और x> 10)

(iv) A = {x:x संख्या 10 का एक गुणज है}

B= {10, 15, 20, 25, 30, …)

हल :

(i) A और B दोनों समुच्चयों के अवयव a, b, c, d हैं … A = B.

(ii) अवयव 12 A में है परन्तु B में नहीं है … A B

(iii) A और B दोनों समुच्चयों में अवयव 2, 4, 6, 8 और 10 हैं।

A=B

(iv) A = 110, 20, 30, 40,…J, B = (10, 15, 20, 25, 30, …)

158 B परन्तु 15 A.A # B.

क्या निम्नलिखित समुच्चय युग्म समान हैं कारण सहित बताइए।

(i) A = {2, 3,}

B= {x 😡 समीकरण + 5x + 6 = 0 का एक हल है}

(ii) A = {x: x शब्द FOLLOW का एक अक्षर है}

B = {y:y शब्द WOLF का एक अक्षर है}

हल :

(i) A = {2, 3}, B = x : – समीकरण :- + 5x + 6 = 0} = {-2, – २}

स्पष्ट है कि समुच्चय A और B के अवयव भिन्न है।

. A=B

(ii) A = {F, O, L, W}, B = {W, O, L, F}

समुच्चय A.और B के अवयव समान हैं।

.. A = B

नीचे दिये गए समुच्चयों में से समान समुच्चयों का चयन करें

A = {2, 4, 8, 12}, B = {1, 2, 3,4}, C = {4, 8, 12, 14}

D = { 3,1, 4, 2}, E = {-1,1}, F = {0, 3},

G = { 1,-1}, H = { 0, 1}

हल :

(क) समुच्चय B और D के अवयव 1, 2, 3,4 हैं।

… B = D

(ख) समुच्चय E और G में – 1, 1 अवयव समान हैं। .. E = G

प्रश्नावली 1.3

रिक्त स्थानों में प्रतीक – या ¢ को भर कर सही कथन बनाइए

(i) {2, 3,4}….. {1, 2. 3. 4. 5}

(ii) ka, b, c} ….{b, c, d}

(iii) {x 😡 आपके विद्यालय का कक्षा XI का एक विद्यार्थी) … {xx आप के

विद्यालय का एक विद्यार्थी}

(iv) {x:x किसी समतल में स्थित एक वृत है}… {x 😡 एक समान समतल में एक

वृत है जिसकी त्रिज्या 1 इकाई है।

(v) {xx किसी समतल में स्थित एक त्रिभुज है}… {x 😡 किसी समतल में स्थित

एक आयत है।

(vi) {x 😡 किसी समतल में स्थित एक समबाहु त्रिभुज है … {xx किसी समतल

में स्थित एक त्रिभुज है) (vii) {xx एक सम प्राकृत संख्या है} … {x 😡 एक पूर्णांक है।

हल :

(i) अवयव 2, 3, 4 0 {1, 2, 3, 4,5}

= {2, 3, 4} c{1, 2, 3, 4, 5}

(ii) {a, b,c) का अवयव 4 {b, c, d]

. . {a, b, c) c {b, c, d}

(iii) जो विद्यार्थी स्कूल की XI कक्षा में है वे स्कूल में भी हैं।

.. {: :: स्कूल की XI कक्षा का विद्यार्थी) ch: x, स्कूल का विद्यार्थी)

(iv) समुच्चय {x ::, समतल में एक वृत्त) के एक अवयव वृत्त की त्रिज्या 1 से भिन्न

हो सकती है।

.. {: :: समतल में वृत्त) C {: : -, वृत्त की त्रिज्या 1 इकाई है।

(v) त्रिभुजों का समुच्चय आयतों के समुच्चय से बिल्कुल भिन्न है।

.:. :समतल में एक त्रिभुज cxx, समतल में एक आयत

(vi) प्रत्येक समबाहू त्रिभुज एक त्रिभुज है।

… {x : X, समतल में एक समबाहू त्रिभुज) cx:, समतल में एक त्रिभुज

(vii) प्रत्येक सम प्राकृत संख्या एक पूर्णांक है।

… {x :x, एक सम प्राकृत संख्या} c {: ::, एक पूर्णांक

.2. जाँचें कि निम्नलिखित कथन सत्य है अथवा असत्य है

(i) {a, b} c {b, c, al

(ii) {a, e} = {x:x अंग्रेजी वर्णमाला का एक स्वर है}

(iii) {1, 2, 3} c {1, 3, 5}

(iv) {a} c {a, b, c} (v) {a} e la, bc

(vi) {x:x संख्या 6 से कम एक सम प्राकृत संख्या है| c {x:x एक वृत्त संख्या

है, जो संख्या 36 को विभाजित करती है}

हल :

(i) समुच्चय {a, b के अवयव a, b दोनों समुच्चय {b, c, a) में है।

.. {a, b} ¢ {b, c, a} असत्य है।

(ii) a, e, दोनों ही स्वर है।

… {a,e} c {x : ४, अंग्रेजी वर्णमाला का स्वर है।

यह कथन सत्य है।

(iii) समुच्चय (1, 2, 5, और {1, 3, 5} में अवयव 2 समुच्चय {1, 3, 5} नहीं है।

.:. {1, 2, 5, c {1, 3, 5)

यह कथन असत्य है।

(iv) ME {a, b,c … {a} c {a, b, c},

यह कथन सत्य है।

(v) {a} समुच्चय है, अवयव नहीं है।

.. {a E {a, b, c}

यह कथन असत्य है।

(vi) सम प्राकृत संख्या 2, 4, संख्या 6 से कम है तथा 36 को विभाजित करती है।

…( X:X, एक सम प्राकृत संख्या है जो 6 से कम है।)

(x:x : 1, एक सम प्राकृत संख्या 36 को विभाजित करती है।)

यह कथन सत्य है।

मान लिजिए कि A = {1, 2, 3, 4}, 5} निम्नलिखित में से कौन सा कथन सही नहीं, है और क्यों?

(i) { 3,4} CA. (ii) {3,4} E A (iii) {{3, 4}} CA

(iv) 1 € A (v) 1 CA (vi) {1, 2, 5} CA

(vii) {1, 2,5} E A (viii) { 1, 2, 3} CA

(ix) | E A (x) C A. (xi) {4} CAT

हल :

(i) सही नहीं है। समुच्चय {3, 4} एक अवयव है।

(ii) सही है। क्योंकि {3,4} समुच्चयं A का एक अवयव है।

(iii) सही है। :: A के अवयव {3, 4} का एक उपसमुच्चय है।

(iv) 1 E A, सही है।

(v) 1 CA सही नहीं है क्योंकि 1 एक समुच्चय नहीं है। .

(vi) {1,2,5} C A सही है। समुच्चय {1,2,5} के अवयव 1, 2, 5 समुच्चय A में हैं।

(vii) {1, 2, 5} E सही नहीं है। {1, 2, 5) अवयव नहीं है। यह एक समुच्चय है। ”

(viii) {1, 2, 3} CA सही नहीं है। अवयव 3 समुच्चय में नहीं है।

(ix) E A, सही नहीं है। के एक समुच्चय है, अवयव नहीं है। ।

(x) , CA सही है। • सभी समुच्चयों का उपसमुच्चय है।

(xi) {4) CA सही नहीं है। {0} समुच्चय का समुच्चय है।

निम्नलिखित समुच्चयों के सभी उपसमुच्चय लिखें

(i) {a}

(ii) {a, b}

(iii) {1, 2, 3}

(iv) के

हलं : (i) {a}, (ii). p. {a}, {b}, {a, b} (iii) +, {1}, {2}, {3}, {1, 2}, {2, 3}, {1,3}, {1, 2, 3) (iv) 0

P (A) के कितने अवयव हैं यदि A = @ ?

हल : A = p, P (A) = + इस प्रकार P (A) का 20 = 1 अवयव है।

निम्नलिखित को अंतराल रूप में लिखें

(i) {x : * ER, – 4 <xs6} (ii) {x 😡 E R, – 12 < x < – 10

(iii) {x :X ER,0 <x <7} .. .. (iv) {x: xER,352 <4}

हल : वांछित अंतराल इस प्रकार हैं

(i) (-4,6] (ii) (-12, – 10)

(iii) [0,7) (iv) [3,4]

निम्नलिखित अंतरालों को समुच्चय निर्माण रूप में लिखें

(i) (-3,0) (ii) [6, 12]

(iii) (6,12] (iv) [-23,5)

हल :

(i) (-3,0) = {x : x E R, – 3 <3 < 0}

(ii) [6, 12] = {x 😡 & R,6 < x < 12}

(iii) (6, 12] = {: :: R, 6 <3 < 12} A M

(iv) [-23, 5) = {x : X ER, – 23 <3 <5}

निम्नलिखित में से प्रत्येक के लिए आप कौन सा सार्वत्रिक समुच्चय प्रस्तावित करेंगे?

(i) समकोण त्रिभुजों का समुच्चय

(ii) समाद्विबाहु त्रिभुजों का समुच्चय

हल : दोनों समुच्चयों के लिए सार्वत्रिक समुच्चय-,{x:x 1, समतल में एक त्रिभुज)

समुच्चय A = {1, 3, 5}, B = { 2, 4, 6} और C = {0, 2, 4, 6, 8} प्रदत्त हैं। इन तीनों

समुच्चयों A, B और C के लिए निम्नलिखित में से कौन सा (से) सार्वत्रिक समुच्चय लिए जा सकते हैं?

(i) {0,1,2,3,4,5,6} (ii) . ᵠ

(iii) {0, 1,2,3,4,5,6,7,8,9,10} (iv) {1, 2, 3,4,5,6,7,8}

हल :

समुच्चय (iii),

तीनों समुच्चय A, B,C के लिए {0,1,2,3,4,5,6,7,8,9,10} सार्वधिक समुच्चय है।

प्रश्नावली 1.4

निम्नलिखित में से प्रत्येक समुच्चय युग्म का सम्मिलन ज्ञात करें

(i) X = { 1, 3,5}, Y = {1, 2, 3}

(ii) A = {a, e, i, 0, u}, B = {a, b,c}

(iii) A = {x:x एक प्राकृत संख्या है और 3 का गुणज है}

B= {x:x संख्या 6 से कम एक प्राकृत संख्या है

(iv) A = {x:x एक प्राकृत संख्या है और 1<x <6}: 1

B = {x 😡 एक प्राकृत संख्या है और 6<x<10} .

(v) A = {1,2,3}, B = ᵠ

हल :

(i) X Y = {1, 3, 5} {1, 2, 3} = { 1, 2, 3,5}

(ii) A U B = {a, e, i, 0, u}, {a, b, c)

= {a, b, c, e, i, o, u)

(iii) A U B = {3, 6, 9….} U {1, 2, 3, 4, 5)

= {1, 2, 3, 4, 5, 6, 9, 12 ….)

(iv) AUB = {2, 3, 4, 5, 6} {7, 8, 9)

= {2, 3, 4, 5, 6,7,8,9}

(v) A U B = { 1, 2, 3} = { 1, 2, 3}

मान लीजिए कि A = {a, b}, B = {a, b, c} क्या ACB? AUB ज्ञात करें

हल : A = {a, b}, B = {a, b, c)

समुच्चय A के अवयव a, b समुच्चय B में भी हैं।

.. A U B = A U B = B

और A U B = {a, b} {a, b, c} = {a, b, c)

यदि A और B दो ऐसे समुच्चय हैं कि A C B तो AUB क्या हैं?

हल : A C B = समुच्चय A के सभी अवयव समुच्चय B में हैं।

A U B = B

यदि A = {1, 2, 3, 4,}; B = {3,4,5,6}; C = {5, 6, 7, 8} और D = { 7, 8, 9, 10} तो

निम्नलितिखत ज्ञात करें

(i) AUB (ii) AUC (iii) BUC (iv) BUD

(v) AU BUC (vi) AU BUD (vii) BUCUD

हल :

(i) AU B = {1,2,3,4} {3,4,5,6)

= {1,2,3,4,5,6}.

(ii) A U C = {1, 2, 3,4,5} 0 {5,6,7,8}

= { 1, 2, 3, 4, 5, 6, 7, 8}.

(iii) B U C = {3,4,5,6} {5,6,7,8}

= {3,4,5,6,7,8}.

(iv) B O D = { 3,4,5,6,017,8,9, 10}

= {3,4,5,6,7,8,9,10).

(v) A U B U C = (11, 2, 3,4} {3,4,5,6}){5,6,7,8)

= {1, 2, 3,4,5,6} 0 {5,6,7,8}

= (1,2,3,4,5,6,7,8}….

(vi) A U B U D = ({1, 2, 3, 4, 5) 0 {3, 4, 5, 6)017, 8, 9, 10}

= [1, 2, 3, 4, 5,6} {7, 8, 9, 10)

= [1, 2, 3, 4, 5, 6, 7, 8, 9, 10).

(vii) B U C U D = (13, 4, 5, 60 {5, 6,7,8}) (7,8,9,101

= 1 3, 4, 5, 6, 7, 80 (7,8,9,10)

={3,4,5,6,7,8,9,10]…

प्रश्न 1 में दिए प्रत्येक समुच्चय युग्म का सर्वनिष्ठ समुच्चय ज्ञात करें

हल :

(i) X ∩ Y = { 1, 3, 5} ∩ {1, 2, 3} = { 1, 3)

(ii) A ∩ B = {a, e,i,o,u) ∩ {a, b, c} = {a} ‘

(iii) A ∩ B = {3, 6,9…..} ∩ {1, 2, 3, 4, 5) = {3}

(iv) A ∩ B = {2, 3, 4, 5, 6} ∩ {7,8,9} = ɸ

(v) A ∩ B = {1, 2, 3} = ɸ

यदि A = {3, 5, 7, 9, 11}; B = {7, 9, 11, 13}; C = {11, 13, 15} और D = { 15, 17}

तो निम्नलितिखत ज्ञात करें- .

(i) A ∩ B (ii) B ∩ C (iii) A ∩ C ∩ D ‘,

(iv) A ∩ C (v) B ∩ D. (vi) A∩ (B U C)

(vii) A ∩ D (viii) A ∩ (B U D) (ix) (A ∩ B) ∩ (B U C)

(x) (AUD) ∩ (B U C)

हल::

(i) A ∩ B = {3,5,7,9, 11} ∩ {7, 9, 11, 13) = {7,9, 11}.

(ii) B ∩ C = {7, 9, 11, 13,2{11, 13, 15} = {11, 13}.

(iii) A ∩ C ∩ D = (13, 5, 7, 9, 11} ∩ { 11, 13, 15}) ∩ {15, 17)

= {11} ∩ {15, 17} = h.

(iv) A ∩ C = { 3, 5, 7, 9, 11} ∩ {11, 13, 15) = {11}.

(v) B ∩ D = {7, 9, 11, 13} ∩ {15, 17} =

(vi) A ∩ (B U C) = {3, 5, 7, 9, 11} ∩ ({7, 9, 11, 13} U {11, 13, 15})

= {3, 5, 7, 9, 11} ∩ {7,9, 11, 13, 15)

= {7,9, 11}.

(vii) A ∩ D = {3, 5, 7, 9, 11} ∩ {15, 17} = ɸ

(viii) A ∩ (B U D) = {3,5,7,9, 11} ∩{7,9, 11, 13} {15, 17}

= {3, 5, 7, 9, 11} {7,9, 11, 13, 15, 17}

= {7,9, 11}. :

(ix) A ∩ B = {3, 5, 7, 9, 11} ∩ {7, 9, 11, 13} = {7, 9, 11}

B U C = {7, 9, 11, 13} 0 {11, 13, 15} = {7,7, 11, 13, 15)

(A ∩ B) (B U D) = {7, 9, 11} 0 {7, 9, 11, 13, 15)

. = {7, 9, 11}.

(x) A U D = {3, 5, 7, 9, 11} ∩ {15, 17) .

= {3, 5, 7, 9, 11, 15, 17} . B U C = {7,9, 11, 13} {11, 13, 15)

= {7,9, 11, 13, 15)

(A U B) ∩ ( B U C) = {3, 5, 7, 9, 11, 15, 17} ∩ {7,9, 11, 13, 15}

= {7, 9, 11, 15)

यदि A = {x 😡 एक प्राकृत संख्या है)

B = {x 😡 एक सम प्राकृत संख्या है)

C = {x:x एक विषम प्राकृत संख्या है)

D = {x 😡 एक अभाज्य संख्या है तो निम्नलिखित ज्ञात करें

(i) A ∩ B (ii) A ∩ C (iii) A ∩ D

(iv) B ∩ C (v) B ∩ D (vi) C ∩ D

हल : A = {x:x एक प्राकृत संख्या हैं) = {1, 2, 3, 4,…)

B = {x:x एक सम प्राकृत संख्या हैं) = {2, 4, 6, 8, …}

C = {x:x एक विषम प्राकृत संख्या हैं) = {1, 3, 5, 7, …}

D = {x:x एक अभाज्य संख्या हैं) = { 2, 3, 5, 7, 11, …)

(i) A B = {1, 2, 3, 4, …} ∩ {2, 4, 6, 8, …}

= {2, 4, 6, 8, …} = C.

(ii) A ∩ C = {1, 2, 3, 4, …} ∩ {1, 3, 5, 7, …}

= { 1, 3, 5, 7, …} = C

(iii) A ∩ D = { 1, 2, 3, 4, …} ∩ {2, 3, 5, 7, …)

={ 2, 3, 5, 7, …} = D

(iv) B ∩ C = {2, 4, 6, 8, …} ∩ {1, 3, 5, 7, …}

=ɸ

(v) B ∩ D = {2, 4, 6, 8, …} ∩ {2, 3, 5, 7, …}

= {2}.

(vi) C ∩ D = {1, 3, 5, 7, …} ∩ {2, 3, 5, 7, 11, …)

= {3,5,7, 11, 13, …}

= {x : : एक विषम अभाज्य संख्या}

निम्नलिखित समुच्चय युग्मों में से कौन से युग्म असंयुक्त है।

(i) {1, 2, 3, 4} तथा {x:x एक प्राकृत संख्या है और 45x<6}

(ii) {a, e, i, 0, u} तथा {c,d,e,f}.

(iii) {x 😡 एक सम पूर्णांक है और {x 😡 एक विषम पूर्णांक है}

हल :

(i) मान लीजिए A = {1, 2, 3,4}

B = {x : – एक प्राकृत संख्या और 4 < < 6}

= {4, 5, 6}

अवयव 4, A और B दोनों समुच्चयों में हैं।

A और B असंयुक्त नहीं हैं।

(ii) दिये हुए समुच्चयों में अवयव e उभयनिष्ठ हैं।

यह असंयुक्त समुच्चय नहीं हैं।

(iii) मान लीजिए A= {: : : एक सम पूर्णांक हैं।

= {… -4, -2, 0, 2, 4, …)

B = {x:x एक विषम पूर्णांक हैं।

= {..,. -5, -3,-1, 1,3,5,…}

A और B समुच्चयों में कोई भी अवयव उभयनिष्ठ नहीं हैं।

यह समुच्च्य असंयुक्त हैं।

यदि A = {3,6, 9, 12, 15, 18,21}; B = {4, 8, 12, 16, 20};

C = {2,4,6,8,10,12, 14, 16}; D = {5, 10, 15, 20}

तो निम्नलिखित को ज्ञात करें

(i) A – B (ii) A -C (iii) A -D (iv) B-A

(v)C-A (vi) D-A (vii) B-C (viii) B-D

(ix) C-B (x) D-B (xi) C-D (xii) D-C

हल :

(i) A – B = {3, 6, 9, 12, 15, 18,21) – {4,8, 12, 16, 20}

= {3,6, 9, 15, 18, 21)

(ii) A – C = {3,6, 9, 12, 15, 18, 21} – {2,4, 6, 8, 10, 12, 14, 16)

= {3,9, 15, 18, 21)

(iii) A – D = {3, 6,9, 12, 15, 18,21} – {5, 10, 15, 20}

= {3, 6, 9, 12, 18, 21)

(iv) B – A = {4, 8, 12, 16, 20} – {3, 6, 9, 12, 15, 18, 21)

= {4, 8, 16, 20}

(v) C – A = {2, 4, 6, 8, 10, 12, 14, 16} – {3, 6, 9, 12, 15, 18, 21)

= {2, 4, 8, 10, 14, 16

(vi) D – A = {5, 10, 15, 20} – {3, 6, 9, 12, 15, 18, 21}

= {5, 10, 20}

(vii) B – C = {4, 8, 12, 16, 20} – {2, 4, 6, 8, 10, 12, 14, 16}

= {20)

(viii) B – D = {4, 8, 12, 16, 20} – {5, 10, 15, 20}

= {4, 8, 12, 16)

(ix) C – B = {2, 4, 6, 8, 10, 12, 14, 16} – {4, 8, 12, 16, 20}

= {2,6, 10, 14)

(x) D – B = {5, 10, 15, 20} – {4, 8, 12, 16, 20}

= {5, 10, 15)

(xi) C- D = 2, 4, 6, 8, 10, 12, 14, 16} – {5, 10, 15, 20}

= {2, 4, 6, 8, 12,14, 16)

(xii) D-C = {5, 10, 15,20} – {2, 4, 6,8, 10, 12, 14, 16},

= [5, 15, 20/

यदि x = la, b, cul और Y =1f,b, d.gl तो निम्नलिखित को ज्ञात करें

(i)Y-Y (ii)Y-X (iii)X ∩ Y

हल :

(i) X – Y = {a, b, c, d} – {f, b, d, g} = {a, c}

(ii) Y – X = {f,b, d,g} – {a, b, C, d} = {f.g}

(iii) X Y = {a, b, c,d}o{f,b, d, g} = {b, d}

यदि R वास्तविक संख्याओं और Q परिमेय संख्याओं के समुच्चय है, तो R-Q

क्या होगा।

हल : R = x : : एक वास्तविक संख्या हैं।

Q = {: : : एक परिमेय संख्या हैं।

R – Q = {: : : एक अपरिमेय संख्या हैं।

= यह अपरिमेय संख्याओं का समुच्चय है।

बताइए कि निम्नलितिखत कथनों में से प्रत्येक सत्य है या असत्य अपने उत्तर का

औचित्य भी बताइए।

(i) {2, 3, 4, 5} तथा {3, 6} असंयुक्त समुच्चय हैं

(ii) {a, e, i, 0, u} तथा {a, h, e, d} असंयुक्त समुच्चय हैं

(iii) {2, 6, 10, 14} तथा {3,7, 11, 15} असंयुक्त समुच्चय हैं

(iv) {2,6, 10} तथा {3, 7, 11} असंयुक्त समुच्चय हैं

हल :

(i) कथन सत्य नहीं है क्योंकि समुच्चय {2, 3, 4, 5) और (3, 6) में अवयव 3

उभयनिष्ठ हैं।

(ii) कथन सत्य नहीं है क्योंकि समुच्चय {a, e, i, 0, u} और {a, b, c, d} में अवयव

। उभयनिष्ठ हैं।

(iii) कथन सत्य है यह समुच्चय असंयुक्त हैं।

समुच्चय {2, 6, 10, 14} और {3,7, 11, 15) में कोई अवयव उभयनिष्ठ नहीं हैं।

.. यह समुच्चय असंयुक्त है।

(iv) कथन सत्य है।

समुच्चय (2,6, 10) और {3,7, 11} में कोई अवयव समान नहीं हैं।

⸫ यह समुच्चय असंयुक्त हैं।

प्रश्नावली 1.5

मान लीजिए कि U = {1,2,3,4,5,6,7,8,9), A = {1,2,3,4), B = {2,4,6,8} और

C= {3,4,5,6} तो निम्नलिखित ज्ञात करें

(i) A (ii) B’ (iii) (A U C)

(iv) (A U B)’ (v) (A)’ (vi) (B – C)

हल : (i) A’ = U – A

= [1, 2, 3,4,5,6,7,8,9} – {1, 2, 3,4}

= {5, 6, 7, 8, 9)

(ii) B’ = U-B

= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 4, 6, 8}

= {1, 3, 5, 7,9}

(iii) AUC = {1, 2, 3, 4} {3, 4, 5, 6}

= {1, 2, 3, 4, 5, 6)

⸫ (A U C) = U – (A U C)

= {1, 2, 3,4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 5, 6}

= {7, 8,9)

(iv) AU B = {1, 2, 3, 4} U {2,4,6,8}

= { 1, 2, 3, 4, 6, 8}

(A U B) = U – (A O B)

= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 2, 3, 4, 6, 8}

= {5,7,9}

(v) (A’) = U – A’

= {1, 2, 3, 4, 5, 6, 7, 8, 9) – {5, 6, 7, 8, 9}

= {1, 2, 3,4}

(vi) B – C = {2,4,6,8} – {3,4,5,6} = {2,8}

(B – C’) = U – (B – C)

= {1, 2, 3,4,5,6,7,8,9} – {2, 8}

= {1, 3, 4, 5, 6, 7,9}

यदि U = {a, b, c,d,e,f,g, h} तो निम्नलिखित समुच्चयों के पूरक ज्ञात करें

(i) A = {a, b, c} (ii) B = {d,e,f,g}

(iii)C = {a, c,e,g} (iv) D = {f.g, h, al

हल :

(i) A = U-A

= {a, b, c,d,e,f,g, h} – {a, b, c)

= {d,e,f, g, h} (ii) B’ = – B = {a, b, c,d,e,f,g, h} – {d, e,f, g}

= { a, b, C, 1} (iii) C’ = U-C

= {a, b, c,d,e,f,g, 1} – {a, c, e, g} = {b, d,f, h} (iv) D’ = u – D .

_ = {a, b, c,d,e,f, g, h} – If, g, h, a} = {b, c, d, e}

प्राकृत संख्याओं के समुच्चय को सार्वत्रिक समुच्चय मानते हुए, निम्नलिखित

समुच्चयों के पूरक लिखें

(i) {x 😡 एक प्राकृत सम संख्या है}

(ii) {x 😡 एक प्राकृत विषम संख्या है}

(iii) {x: x संख्या 3 का एक धन गुणज है}

(iv) {x :- एक अभाज्य संख्या है?

(v) {x : x, 3 और 5 से विभाजित होने वाली एक संख्या है।

(vi) {x : x एक पूर्ण वर्ग संख्या है}

(vii) {xx एक पूर्ण धन संख्या है}

(viii) {x: x + 5 = 8} (ix) {x : 2x + 5 = 9} (x) {x:x27}

(xi) {x : XEN और 2x + 1> 10}

हल :

(i) {x:x एक विषम संख्या है।

(ii) {x:x एक सम संख्या है।

(iii) {x:x E N, और : संख्या 3 का धन गुणज नहीं है}

(iv) {x:x= 1 और : एक घन भाज्य संख्या है।

(v) {x:x E N और :, संख्या 3 व 5 किसी से भी विभाजित नहीं होती

(vi) {x : X E N तथा x एक पूर्ण वर्ग संख्या नहीं हैं।

(vii) {x : X EN तथा x एक पूर्ण घन संख्या नहीं हैं।

(viii) (x:x € N 79T x ≠ 3}

(ix) {x:x E N तथा x ≠2}

(x) {x:x E N तथा x < 7}

(xi) {x:x E N तथा x <9/2)

यदि U = {1, 2, 3, 4, 5, 6, 7, 8, 9} A = {2, 4, 6, 8,) और B= {2, 3, 5, 7} .

तो सत्यापित करें

(i) (A U B) = A ∩ B’

(ii) (A ∩ B) = A U B

हल :

(i) A U B = {2, 4, 6, 8} {2, 3, 5, 7}

= {2, 3, 4, 5, 6, 7, 8}

बायां पक्ष = (A U B) = U – (AU B)

= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 3, 4, 5, 6, 7, 8}

= (1,9) A’

A = U-A

= {1, 2, 3,4,5,6,7,8,9} – {2, 4, 6, 8}

= {1,3,5,7,91 B’ = U – B

= {1, 2, 3, 4, 5, 6, 7, 8, 9} – {2, 3, 5, 7}

= {1, 4, 6, 8, 9

दायाँ पक्ष = A ∩ B

= {1, 3,5,7,9} {1, 4, 6, 8, 9}

= {1, 9} 3775d (A U B)’ = A’ B’

(ii) बायां पक्ष = (A ∩ B)’

अब (A ∩ B = {2, 4, 6,8} ∩ {2,3,5,7} = {2}

(A ∩ B) = U – (A ∩ B)

= { 1, 2, 3,4,5,6,7,8,9} – {2}

= { 1, 3, 4, 5, 6, 7, 8, 9)

आगे A U B’ = {1,3,5,7,90 ) U {1, 4, 6,8,9) [(i) और (ii) से]

इस प्रकार (A ∩ B)’ – A U B’.

निम्नलिखित में से प्रत्येक के लिए उपयुक्त वेन आरेख खींचे

(i) (A U B) (ii) A ∩ B’ (iii) (A ∩ B) (iv) (A U B’)

हल : छायांकित क्षेत्र अभीष्ठ समुच्चयों को दर्शाते हैं

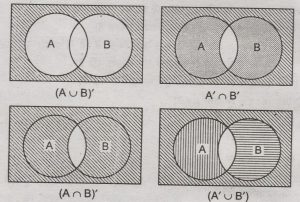
(A U B) A’ ∩ B’

PHOTO

(A ∩ B) (A U B’)

मान लीजिए कि किसी समतल में स्थित सभी त्रिभुजों का समुच्चय सार्वत्रिक

समुच्चय U हैं।

यदि A उन सभी त्रिभुजों का समुच्चय हैं जिन में कम से कम एक कोण 60° से भिन्न हैं, तो A’ क्या है?

हल : U = {x 😡 समतल में एक त्रिभुज है।

A = {x : x एक त्रिभुज जिस का कम से कम एक कोण 60° का न हो ..

A’ = (सभी समबाहु त्रिभुजों का समुच्चय)

निम्नलिखित कथनों को सत्य बनाने के लिए रिक्त स्थान भरिए

(i) A U A = …..

(ii) Cɸ ∩ A = ……..

(iii) A ∩ A = …..

(iv) UMA = …….

हल :

(i) A U A’ = u

(ii)ɸ ∩ A = U ∩ A = A

(iii) A ∩ A’ = ɸ

(iv) U ∩ A = ɸ ∩ A = ɸ

प्रश्नावली 1.6

यदि X और Y दो ऐसे समुच्चय हैं कि 1(X) = n(Y) = 23 तथा n(XUY)= 38, तो

n(X∩Y) ज्ञात कीजिए।

हल : n(X∩Y) = n(X) + n(Y) – n(X∩Y)

या, 38 = 17 +23 – n(X∩Y)

= 40 – X (X∩Y )

या, n(X∩Y) = 40 – 38 = 2

2.यदि x और Y दो ऐसे समुच्चय हैं कि XUY में 18,X में 8 और Y में 15 अवयव हों तो X∩Y में कितने अवयव होंगें?

हल : n(X) = 8,n(Y) = 15 और n(XUY) = 18

हम जानते हैं कि

n(XUY) = n(X) + n(Y)- n(X∩Y)

या, 18 = 8 + 15- n(X∩Y) = 23 – 1(X∩Y)

या, n(X∩Y) = 23-18 = 5

400 व्यक्तियों के समूह में, 250 हिन्दी तथा 200 अंग्रेजी बोल सकते हैं। कितने

व्यक्ति हिन्दी तथा अंग्रेजी बोल सकते हैं।

हल : मान लीजिए कि H और E क्रमश: हिन्दी व अंग्रेजी बोलने वालों के समुच्चय

n(H) = 250,n (E) = 200

और n(HUE)= 400

अब n(HU E) = n (H) + n(E)- n(HUE)

400 = 250 + 200 – n(HUE) = 450 – n(HUE)

n(HUE) = 450-400 = 50

यदि S और T दो ऐसे समुच्चय हैं कि S में 21, T में 32 और ST में 11 अवयव

हो तो SUT में कितने अवयव होंगे?

हल : यहाँ n (S) = 21, n (T) = 32, n(S∩T) = 11

n(SUT) = n (S) + n (T)- n(S∩T)

= 21 + 32-11 = 53-11 = 42.

यदि x और Y दो ऐसे समुच्चय हैं कि X में 40,XUY में 60 और XOY में 10

अवयव हों तो Y में कितने अवयव होंगें?

हल : n(X) = 40, n(XUY) = 60,n(X∩Y) = 10, n(Y) = ?

अब (XUY) =n(X) + n(Y)- n(X∩Y)

या, 60 = 40+ n(Y)- 10

n(Y) = 60-40 + 10 = 30

70 व्यक्तियों के समूह में 37 कॉफी, 52 पाय पसंद करते हैं और प्रत्येक व्यक्ति

दोनों में से कम से कम एक पेव पसंद करता है, तो कितने व्यक्ति कॉफी और काय दोनों पसंद करते हैं।

हल : मान लिया C, कॉफी पीने वाले लोगों के समुच्चय को और T, चाय पीने वाले लोगों के समुच्चय दर्शातें हैं।

अब n(CUT) = 70, n(C) = 37, n(T) = 52

n(CUT) = n(C) + n(T) – n(CUT)

या, 70 = 37 + 52 – n(CUT)

.. . n(CUT) = 37 + 52-70 = 89-70 = 19.

65 व्यक्तियों के समूह में, 40 व्यक्ति क्रिकेट और 10 व्यक्ति क्रिकेट तथा टेनिस

दोनों को पसंद करते हैं, तो कितने व्यक्ति टेनिस को पसंद करते हैं किंतु क्रिकेट नहीं? कितने व्यक्ति टेनिस को पसंद करते हैं?

हल : मान लिया C, क्रिकेट पसंद करने वाले लागों का समुच्चय है और T टेनिस पसंद करके वालों का समुच्चय है।

अब n (CUT) = 65, n (C) = 40, n(C∩T) = 10

हम जानते हैं n (CUT) = n (C) + n(T) – n(C T)

या, 65 = 40 + n(T) – 10 = 30 + n(T)

… n(T) = 65 – 30 = 35

केवल टेनिस पसंद करने वालों की संख्या = n(T) – 1(CUT) = 35-10 = 25

इस प्रकार टेनिस पसंद करने वालों की संख्या जो क्रिकेट पसंद नहीं करते = 25

टेनिस पसंद करने वाले लोगों की संख्या = 35

एक कमेटी में, 50 व्यक्ति बॅच 20 व्यक्ति स्पेनिश और 10 व्यक्ति स्पेनिश और बॅच दोनों ही भाषाओं को बोल सकते हैं। कितने व्यक्ति इन दोनों ही भाषाओं में से कम से कम एक भाषा बोल सकते हैं?

हल : मान लो फ्रांसीसी बोलने वाले लोगों के समुच्चय को F से तथा स्पैनिश बोलने वाले लोगों के समुच्चय का S से निरुपित किया है।

दिया है : n(F) = 50, 1 (S) = 20, n(F∩S) = 10

अब (FUS) = n (F) + n (S) – n (F∩S)

‘ = 50 + 20 – 10 = 60

कम से कम एक भाषा बोलने वाले लोगों का संख्या = 60.

अध्याय-1 पर विविध प्रश्नावली |

निम्नलिखित समुच्चयों में कौन किसका उपसमुच्चय है इसका निर्णय कीजिए

A = {x : X ϵ R तथा x2 – 8x + 12 = 0 को संतुष्ट करने वाली सभी वास्तविक

संख्याएँ x}, B = {2, 4, 6}, C = {2, 4, 6, 8, …}, D = {6}

हल : A = {x : x ϵ R, 1 समीकरण :2 – 8x + 12 = 0 को संतुष्ट करता है।

= {2, 6}

B = {2, 4, 6)

C = {2, 4, 6, 8, …]

D = {6}

समुच्यय A के अवयव 2, 6 समुच्चय B में भी हैं।
= AcB

इस प्रकार समुच्चय A के अवयव 2,6 समुच्चय C में भी हैं

= AꞇC

समुच्चय B के अवयव 2, 4, 6 समुच्चय C में हैं। .

= Bꞇc

(iv) समुच्चय D का अवयव 6, समुच्चय A, B और C में हैं।

.. D ꞇ A, D c B, D cC.

ज्ञात कीजिए कि निम्नलिखित में से प्रत्येक कथन सत्य है या असत्य है। यदि सत्य

है, तो उसे सिद्ध कीजिए। यदि असत्य है तो एक उदाहरण दीजिए।

यदि x ϵ A तथा A ϵ B तो X ϵ B
यदि ACB तथा B ϵ C तो A ϵ C.
यदि A C B तथा B c C तो A c C
यदि A ¢ B तथा B ¢ C तो A ¢ C
यदि x ϵ A तथा A ¢ B तो x ϵ B
यदि A C B तथा x ϵ B तो x ϵ A

हल : (i) असत्य : मान लीजिए A = {1}, B = {{1}, 2)

स्पष्ट है कि 1 ϵ A, A ϵ B परन्तु 14 समुच्चय B क्योंकि 1,B में नहीं है। इस प्रकार दिया हुआ कथन सत्य नहीं है।

(ii) असत्य : मान लीजिए A = {1}, B = {1,2} और C = {{1, 29, 3}

समुच्चय A का अवयव समुच्चय B में हैं ::

A ꞇ B

अवयव {1,2} समुच्चय C में हैं = B ϵ C

परंतु A = {1} समुच्चय C में नहीं है।

.:. कथन A EC सत्य नहीं है।

(iii) सत्य : A c B = यदि x ϵ A तथा X ϵ B

परन्तु B ꞇ A= यदि x ϵ B तथा x ϵ C

.:. यदि x ϵ A तबE C = A ꞇ c

असत्य : मान लीजिए A = {1, 2}, B = {2, 3},C = [1, 2, 5}

समुच्चय A के सभी अवयव 1,2 समुच्चय B में नहीं है

:: A ¢ B

समुच्चय B के सभी अवयव 2, 3 समुच्चय C में नहीं है।

.:. B ϵ C

परंतु समुच्चय A के सभी अवयव 1, 2 समुच्चय C में हैं।

.:. A ꞇ C

इस प्रकार दिया कथन सत्य नहीं है।

असत्य : A = {1, 2}, B = {2, 3, 4, 5}

समुच्चय A के सभी अवयव 1, 2 समुच्चय ? में नहीं है।

.: A ¢ B

समुच्चय A का अवयव 1 समुच्चर B में नहीं है।

.: x ¢ B

सत्य : A ꞇ B = यदि x ϵ A तब 😡 ϵ B

यदि X ¢ B तथा X ϵ A

इस प्रकार कथन A ꞇ B, x ¢ B तब : x ¢ A सत्य हैं।

मान लीजिए A, B और C ऐसे समुच्चय हैं कि AUB = AUC तथा

A ∩ B = A ∩ C तो दिखाएं कि B = C

हल : दिया है A U B = A U C

= (A U B) ∩ C = (A U C) ∩ C = C [(A U C) ∩ C = C)

= (A ∩ C) U (B ∩ C) = C

= (A ∩ B) U (B ∩ C) = C [ARC = A B (दिया है)]

आगे A U B= A U C

(A U B) ∩ B = (A U C) ∩ B

B = (A U C) ∩ B = (A ∩ B) U (C ∩ B )

या (A ∩ B ) U (B ∩ C)= B.

समीकरण (i) और (ii) से B = C प्राप्त होता है।

दिखाएँ कि निम्नलिखित चार प्रतिबंध तुल्य हैं

(i) A ꞇ B (ii) A – B = ϕ (iii) AUB = B (iv) A ∩ B = A

हल : (i) A ꞇ B= समुच्चय A के सभी अवयव B में हैं।

= A – B = ϕ अर्थात् (i) ↔ (ii)

(ii) A – B = ϕ = समुच्चय A के सभी अवयव B में हैं।

↔ AUB = B अर्थात् (ii) ↔ (iii)

(iii) A U B = B ↔ समुच्चय A के सभी अवयव B में हैं.

↔ समुच्चय A और B में समुच्चय A के अवयव उभयनिष्ठ हैं।

… A ∩ B = A

इससे स्पष्ट है कि सभी कथन समान हैं।

दिखाइए कि यदि A ꞇ B तो C – B ꞇ C-A.

हल : X ꞇ C – B ↔x ϵ C परंतु 😡 ¢ B

यह दिया है A ꞇ B = यदि x ¢ B = X ¢ A

अर्थात् x ϵ C और x ϵ A = X ϵ C – A

→ हम देखते हैं कि यदि x ϵ C – B तब x ϵ C – A

= C – B ꞇ C – A.

मान लीजिए कि P(A) = P (B), तो सिद्ध करें कि A = B

हल : मान लीजिए : समुच्चय A का कोई अवयव है।

तब एक उपसमुच्चय X (मान लें) ऐसा होगा जिसमें x ϵ A जिसके अनुसार

X ꞇ A = X ϵ P(A)

= X ϵ P(B) [.. P(A) = P(B ))

X ϵ B या X ϵ B

अर्थात यदि x ϵ A तब X ϵ B = A ꞇ B

आगे, माना Y समुच्चय B का कोई अवयव है।

= तब समुच्चय B का कोई उपसमुच्चय Y (मान लें) होगा जिससे y ϵ Y

Y ꞇ B

Y ϵ P(B) [: P(B) P(A)

Y ꞇ A

यदि Y ϵ B तब Y ϵ A

B ꞇ A

समीकरण (i) और (ii) से हम प्राप्त करते हैं कि A = B

किन्हीं भी समुच्चयों A तथा B के लिए क्या यह सत्य है कि

P (A) U P (B) = P (AUB) अपने उत्तर का औचित्य बताइए।

हल : यह सत्य नहीं है।

A = {a}, B = {b} और A U B = {a,b}

P(A) = {ϕ, {a}}, P(B) = {ϕ, b)

P(A) P(B) = {ϕ, {a}, {b}} (1)

अब A U B = {a, b}

P(A U B) = {ϕ, {a}, {0}, {a, b}} (2)

. समीकरण (i) और (ii) से हम पाते हैं कि P(A) U P(B) # P(A UB)

किन्हीं दो समुच्चयों A तथा B के लिए सिद्ध करें कि A = (A ∩ B) U (A – B) और

A U (B – A)=A U B

हल : (i) दायाँ पक्ष = (A ∩ B) U (A – B)

= (A ∩ B) U (A – B’) [.:. A – B = AN B’]

= A ∩ u (B ∩ B) [वितरक गुण

= A ∩ u [u सार्वत्रिक समुच्चय]

= A

इस प्रकार, (A ∩ B) U (A – B) = A

(ii) बायाँ पक्ष = A U (B – A)

= A U (B ∩ A’) [:. B – A = BOA]

= (A U B) (AU A’) (वितरक गुण)

= (A U B) ∩ n [u सार्वत्रिक समुच्चय]

= A U B

इस प्रकार, A U (B – A) = A U B.

समुच्चय के गुणधर्मों का प्रयोग करके सिद्ध करें कि

(i) A U(A ∩ B) = A (ii) A ∩ (A U B)= A

हल : (i) बायाँ पक्ष = A U(A ∩ B)

= (A U A) ∩ (A U B) (वितरक गुण)

= A ∩ (A U B) [:. A U A = A]

= A [:. A ꞇ A U B)

A U(A ∩ B) = A.

(ii) बायाँ पक्ष = A ∩ (A U B)

= (A ∩ A) (A ∩ B) (वितरक गुण A)

= A U (A ∩ B) [.. AMA = A]

= A (A ∩ B C A]

.. A ∩ B (A U B) = A.

दिखाएँ कि AB= AC का तात्पर्य B = C आवश्यक रूप से नहीं होता है।

हल : माना A = {1,2}, B = {1, 7}, C = {1,4}

A ∩ B = {1, 2}∩ {1, 7} = {1}

A ∩ C = {1, 2}∩ {1,4} = {1}

A ∩ B = A ∩ c

परंतु B ҂ C

= यदि A ∩ B = A ∩ C तो आवश्यक नहीं है कि B = C

मान लीजिए कि A और B समुच्चय हैं। यदि किस समुच्चय X के लिए

A ∩ X = B ∩ X = ϕ तथा A U X= B U X तो सिद्ध करें कि A = B

हल : हमें दिया है A U X = B U X, जबकि X कोई समुच्चय है

= A ∩ (A U X) = A ∩ (B U X) [A ꞇ A U X .. A ∩ (A U X) = A]

= A = A ∩ (B U X) –

= (A ∩ B) U (A ∩ X) (वितरक गुण)

= (A ∩ B) ∩ ϕ [.. दिया है A ∩ X = ϕ]

= A ∩ B

= A ꞇ B … (i)

दूसरा A U X = B U X

= B ∩ (A U X)

= B (B U X) = B

= (A U X) = B [.. B ꞇ B U X]

(B A) U (B n X) = B (वितरक गुण)

(B ∩ A) U ϕ = B [दिया है B ∩ X =]

= (B ∩ A) = B

= B ꞇ C … (ii)

समीकरण (i) और (ii) से हम पाते हैं कि A = B

ऐसे समुच्चय A, B और C ज्ञात कीजिए ताकि A ∩ B, B ∩ C तथा A ∩ C अरिक्त

समुच्चय हों और A ∩ B ∩C = ϕ

हल : माना A = {1, 2}, B = {2, 3}, C = {2, 3}

A ∩ B = {1, 2} ∩ {2, 3} = {2}

B ∩ C = {2, 3} ∩ (1,3} = {3}

C ∩ A = {1,3} ∩ {1, 2′ = {1}

इस प्रकार A ∩ B, B ∩ C,C ∩ A रिक्त समुचय नहीं है।

. A ∩ B ∩ C = (A ∩ B ∩ C = {2,∩ {1, 3} = ϕ

किसी विद्यालय के 600 विद्यार्थियों के सर्वेक्षण से ज्ञात हुआ कि 150 विद्यार्थी चाय,

225 विद्यार्थी कॉफी तथा 100 विद्यार्थी चाय और कॉफी दोनों पीते हैं। ज्ञात कीजिए कि कितने विद्यार्थी न तो चाय पीते हैं और न कॉफी पीते हैं।

हल : मान लिया T और C चाय नीचे वाले तथा कॉफी पीने वाले विद्यार्थियों के समुच्चय

दिया है : n(T) = 150, n(C) = 225, n(TOC) = 100

n(T U C ) = n ( T ) + n ( C ) – n (T ∩ C )

= 150 + 225- 100 = 275

= उन विद्यार्थियों की संख्या जो चाय या कॉफी पीते हैं या चाय और कॉफी दोनों पीते हैं। कुछ विद्यार्थियों की संख्या = 600

.:. उन विद्यार्थियों की संख्या जो चाय या कॉफी कुछ भी नहीं पीते

= 600 – 275 = 325.

विद्यार्थियों के एक समूह में, 100 विद्यार्थी हिन्दी, 50 विद्यार्थी अंग्रेजी तथा 25

विद्यार्थी दोनों भाषाओं को जानते हैं। विद्यार्थियों में से प्रत्येक या तो हिन्दी या अंग्रेजी जानता है। समूह में कुल कितने विद्यार्थी हैं?

हल : मान लीजिए H तथा E क्रमशः हिन्दी जानने वाले और अंग्रेजी जानने वालों के समुच्चय हैं।

दिया है n(H) = 100, n(E) = 50, n(A ∩ E) = 25

n(H U E) = n(H) + n(E) – n(H ∩ E)

= 100 + 50 -25 = 125.

उन विद्यार्थियों की संख्या जो हिन्दी या अंग्रेजी जानते हैं = 125

15: 60 लोगों के सर्वेक्षण में पाया गया कि 25 लोग समाचार पत्र H,26 लोग समाचार , पत्र T,26 लोग समाचार पत्र I,9 लोग H तथा I दोनों, 11 लोग H तथा T दोनों,

8 लोग T तथा I दोनों और 3 लोग तीनों समाचार पत्र पढ़ते हैं, तो निम्नलिखित – ज्ञात करें

कम से कम एक समाचार पत्र पढ़ने वालों की संख्या।
(ii) ठीक-ठीक केवल एक समाचार पढ़ने वालों की संख्या।

हले : मान लिया कि H, T और I उन लोगों के समुच्चयों को क्रमशः दर्शाते हैं जो H समाचार पत्र T समाचार पत्र, I समाचार पत्र पढ़ते हैं।

उन लोगों की संख्या जिनका सर्वेक्षण किया गया = 60

H समाचार पत्र पढ़ने वालों की संख्या = 25

T समाचार पत्र पढ़ने वालों की संख्या = 26

I समाचार पत्र पढ़ने वालों की संख्या = 26

H और I समाचार पत्र पढ़ने वालों की संख्या = 9

H और T समाचार पत्र पढ़ने वालों की संख्या = 11

T और I समाचार पत्र पढ़ने वालों की संख्या = 8

तीनों समाचार पत्र पढ़ने वालों की संख्या = 3

H और I समाचार पत्र पढ़ने वाले तथा T समाचार पत्र न पढ़ने वालों की संख्या

= 9-3 = 6

H और T समाचार पत्र पढ़ने वाले तथा I समाचार पत्र न पढ़ने वालों की संख्या

= 11-3 = 8

T और I समाचार पत्र पढ़ने वाले तथा H समाचार पत्र न पढ़ने वालों की संख्या

= 8-3 = 5

केवल H समाचार पत्र पढ़ने वालों की संख्या = 25 – 8 – 6 – 3 = 8

केवल T समाचार पत्र पढ़ने वालों की संख्या = 26 – 8 – 3 – 5 = 10

केवल I समाचार पत्र पढ़ने वालों की संख्या = 26 – 6 – 3 – 5 = 12

कम-से-कम एक समाचार पत्र पढ़ने वालों की संख्या

= केवल एक समाचार पत्र पढ़ने वालों की संख्या

+ केवल दो समाचार पत्र पढ़ने वालों की संख्या

+ तीनों समाचार पत्र पढ़ने वालों की संख्या

= (8 + 10 + 12) + (8+ 6 + 5) + 3 = 20 + 19 +3

= 52.

दूसरी विधि : n(H U T U I) = n(H) + n(T) + n(1)- n(H ∩ T)

| – (T ∩ I) – n(H ∩ I) + n(H ∩ T ∩ I)

= 25+26 + 26 – 11 -8-9+3

= 77 — 28 + 3 = 80 – 28 = 52.

केवल H और T समाचार पत्र पढ़ने वालों की संख्या = 11-3 = 8

केवल T और I समाचार पत्र पढ़ने वालों की संख्या = 8 – 3 = 5

केवल I और H समाचार पत्र पढ़ने वालों की संख्या = 9-3 = 6

तीनों समाचार पत्र पढ़ने वालों की संख्या = 3

केवल एक समाचार पत्र पढ़ने वालों की संख्या

= 52 – (8 + 5 + 6 + 3) = 52 – 22 = 30.

एक सर्वेक्षण में पाया गया कि 25 लोग उत्पाद A, 26 लोग उत्पाद B, 29 लोग

उत्पाद C पसंद करते हैं। यदि 14 लोग उत्पाद A तथा B, 12 लोग उत्पाद C तथा A,14 लोग उत्पाद B तथा C और 8 लोग तीनों ही उत्पादों को पसंद करते हैं। ज्ञात कीजिए कि कितने लोग केवल उत्पाद C पसंद करते हैं।

हल : दिया है n(A) = 21, n(B) = 26 और n(C) = 29

n(A U B) = 14, n(A U C) = 12

n(B ∩ C) = 14, n(A ∩ B ∩ C)= 8.

अब n(C) = 29,

n(A U C) = 12, n(A ∩ B ∩ C) = 8

.:. n(केवल A और C) = 12-8 = 4

.:. n(केवल B और C) = 14 – 8 = 6

.. (केवल C) = n(C)-n(केवल A और C)

– n(केवल B और C) n(A ∩ B ∩ C)

= 29-4.-6-=8=29-18 = 11.

अन्य महत्वपूर्ण प्रश्न एवं उनके आदर्श उत्तर

सिद्ध करें कि रिक्त समुच्चय ϕ प्रत्येक समुच्चय का उपसमुच्चय होता है।

हल : मान लिया कि ϕ, किसी set A का subset नहीं है।

तो परिभाषा के अनुसार ϕ का कम-से-कम एक element, मान लिया X, ऐसा होगा जो set A का नहीं है।

अर्थात् X ϵ ϕ लेकिन X ɇ A.

लेकिन ϕ एक null set है, … X का element नहीं हो सकता।

अर्थात् ϕ में एक भी ऐसा element नहीं होगा जो A का भी एक element है।

इसलिए यह गलत है कि ϕ, set A का subset नहीं है।

अतः null set c, A का subset होगा, अर्थात् C ꞇ A.

यदि A ꞇ B तथा B ꞇ C, तो सिद्ध करें कि Aꞇc

हल : मान लिया कि set A का एक element : है, अर्थात् :X ϵ A.

चूंकि A ꞇ B – परिभाषा के अनुसार A का हरेक element, B का भी एक element होगा।

X ϵ B अर्थात् . X ϵ A =X ϵ B.

फिर इसी प्रकार चूंकि B ꞇ C…X ϵ B = X ϵ C.

अतएव -X ϵ A = x ϵ C

. .. set A, C का एक subset है अर्थात् A ꞇ C.

यदि A ꞇ B, तो सिद्ध करें कि P(A) ꞇ P(B).

हल : मान लिया कि X ϵ P(A), तो परिभाषा के अनुसार, X ꞇ A

= x ꞇ B (: A ꞇ B)

= X ϵ P(B).

इस प्रकार, X ϵ P(A) = X ϵ P(B). अतः P(A) ꞇ P(B).

यदि A एवं B दो समुच्चय हों तो सिद्ध करें कि P(A ∩ B) = PA) ∩ (B).

हल : मान लिया कि X ϵ P(A ∩ B).

यह = X ꞇ A ∩ B

= X ꞇ A तथा X ꞇ B

= X ϵ P(A) तथा X ϵ P(B)

= X ϵ P(A) ∩ P(B).

इस प्रकार P(A ∩ B) ꞇ P(A) ∩ P(B)

फिर मान लिया कि Y ϵ P(A) ∩ P(B).

तो Y ∩ P(A) तथा Y ϵ P(B)

= Y ꞇ A तथा Y ꞇ B

= Y ꞇ A ∩ B

= Y ϵ P(A ∩ B)

इस प्रकार P(A) ∩ P(B) ꞇ P(A ꞇ B)

समीकरण (1) और (2) से, P(A ∩ B) = P(A) ∩ P(B).

यदि A = {2, 3, 5, 8}, B = {1, 2, 3, 4, 5}, तो (i)A UB (ii)AM B का मान निकालें।

हल : (i) A U B = वह set जिसके elements चाहे A में हों या B में

(या दोनों में हों)

= {1, 2, 3, 4, 5, 8}.

(ii) A ∩ B = वह set जिसके elements दोनों set A और B में शामिल हों।

= {2, 3,5}.

यदि A = {1, 2,3,4,5}, B = {1, 3, 5, 7}, C = {2, 4, 6, 8}, तो (i) (A U B )U C (ii)

A U (B U C) का मान निकालें।

हल : यहाँ (i) में पहले A U B का union निकाला जाएगा और तब इस union को C में सम्मिलन करना होगा।

अतः पहले A U B = {1, 2, 3, 4, 5, 7}

. .. (A U B) U C = {1, 2, 3, 4, 5, 7) U {2, 4, 6, 8}

= {1, 2, 3, 4, 5, 6, 7, 8}

फिर (ii) में पहले B U C का union निकालना होगा और तब इसे A के साथ सम्मिलन किया जाएगा।

B U C = {1, 2, 3, 4, 5, 6, 7, 8} .

A U ( B U C) = {1, 2, 3, 4, 5) U {1, 2, 3, 4, 5, 6, 7, 8}

= {1, 2, 3, 4, 5, 6, 7, 8} .

यदि A = {1, 3, 4, 7, 8}, B = {2, 3, 4, 5}, C = {3, 5, 6, 7},

तो निम्नलिखित का मान निकालें(i) A – B (ii) B – A (iii) B – C (iv) C-B (v) A-C (vi) C-A.

हल : यहाँ (i) A – B = उन सब बिन्दुओं का एक set जो A में है लेकिन B में नहीं

है।

= {1, 7, 8}.

उसी प्रकार, (ii) B – A = उन सब बिन्दुओं का एक set जो B में है लेकिन A में नहीं

है।

= {2,5}.

(iii) B – C = {2, 3} (iv) C – B = {6, 7}

(v) A – C = {1, 3, 8} (vi) C – A = {5, 6}.

यदि A = {1, 2, 3, 4}, B= {1, 3, 5, 7}, C ={3, 5, 7, 8},

तो सिद्ध करें कि A- (B U C) = (A – B) (A – C).

हल : यहाँ B U C = {1, 3, 5, 7, 8}. बायाँ पक्ष = A – (B U C) = {2, 4}.

फिर A – B = {2, 4}, A – C = {1, 2, 4}.

.:. दायाँ पक्ष = (A – B) (A – C) = {2, 4}. Proved.

सिद्ध करें कि (i) A – B = A ∩ B’

(ii) A – B = B’ – A’

हल : (i) मान लिया कि X ϵ A – B, तब X ϵ A – B =X ϵ A और X ɇ B

= X ϵ A और X ϵ B’

=X ϵ A ∩ B’

A – B ꞇ A ∩ B’

फिर मान लिया कि Y ϵ A ∩ B’, तब Y ϵ A ∩ B’ = Y ϵ A और y ϵ B’

= Y ϵ A और y ɇ B

=Y ɇ B और Y ϵ B

= Y ϵ A – B

A ∩ B ꞇ B – A

समीकरण (1) और (2) को मिलाकर हम पाते हैं कि A – B = A ∩ B’.

(ii) मान लिया कि X ϵ A – B, तब x ϵ A – B = X ϵ A और x ɇ B

=X ɇ A’ और x ϵ B’

=x ϵ B’ और y ϵ A

= x ϵ B’ – A’

A – Bc B’ – A

फिर मान लिया की Y ϵ B – A तब Y ϵ B’ – A’, = Y ϵ B’ – और Y ɇ A’

= y ϵ B और Y ϵ A

= y ϵ A और Y ɇ B

= Y ϵ A – B.

B’ – A ꞇ A – B q

समीकरण (1) और (2) से हम पाते हैं कि A – B = B’ – A’.

सिद्ध करें कि (A – B) ∩ (B- A) = ϕ

हल : मान लिया कि x ϵ (A – B) ∩ (B- A),

तब x (A – B) ∩ (B – A) = X ϵ (A – B) और x (B – A).

अब x ϵ A – B =X ϵ A और x ϵ B

x ϵ B – A = x ϵ B और X ϵ A.

इस प्रकार x ϵ (A – B) ∩ (B – A)

= X ϵ A और x ϵ B तथा x ϵ B और x ϵ A

= (x ϵ A और x ɇ A) तथा (x ϵ B और x ɇ B)

= X ϵ ϕ

(A – B) ∩ (B – A) = ϕ.

दूसरी विधि : (A – B) ∩ (B – A) = (A ∩ B’) ∩ (B ∩ A)

= (A ∩ A) ∩ (B ∩ B’) = ϕ ∩ = ϕ

यदि किसी कक्षा के 45% छात्रों ने गणित तथा 85% छात्रों ने जीवविज्ञान लिया हो

तो वर्ग के उन छात्रों का प्रतिशत निकालें जिन्होंने केवल जीवविज्ञान लिया हो।

हल : माना कि M= गणित पढ़नेवाले छात्रों का समुच्चय तथा B=जीवविज्ञान पढ़नेवाले छात्रों का समुच्चय।

यहाँ n(M ∩ B) = 100, n(M) = 45,n(B) = 85.

अब सूत्र से , n(M ∩ B) = n(M) + n(B) – n(M ∩ B)

= 100 = 45 + 85 – 1(M ∩ B) = 100 = 130 – n(M ∩ B)

= n(M ∩ B) = 30%.

केवल 1(B) = n(B) – n(M ∩ B) = 85 – 30 = 55%.

SabDekho

bihar board class 11 math notes | समुच्चय

Leave a Reply Cancel reply

Share this:

Leave a Reply Cancel reply