bihar board class 11 economics | परिक्षेपण के माप
bihar board class 11 economics | परिक्षेपण के माप
( Measures of Disersion)
पाठ्यक्रम (Syllabus)
औसत की सीमाएँ, परिक्षेपण की माप, परिक्षेपण का अर्थ, परिक्षेपण माप की विधियाँ, परिक्षेपण की मापों की गणना तथा उनकी तुलना, सापेक्ष परिक्षेपण तथा निरपेक्ष परिक्षेपण।
इस अध्याय में आप जानेंगे- • मध्यमानों की सीमा की जानकारी • परिक्षेपण के माप को जानने की आवश्यकता • परिक्षेपण के भिन्न माप • माप की गणना करना तथा उनमें तुलना करना • सापेक्ष परिक्षेपण तथा निरपेक्ष परिक्षेपण में तुलना करना।
” याद रखने योग्य बातें (Points to Remember) :-
1. परिक्षेपण (Dispersion)-परिक्षेपण एक ऐसी सांख्यिकीय माप है जिससे किसी श्रृंखला के मदों में अन्तर अथवा मदों के बिखराव की जानकारी मिलती है।
2. परिक्षेपण के माप (Measurement of Dispersion)-(i) विस्तार, (i) चतुर्थक विचलन,
(iii) माध्य विचलन, (iv) प्रमाण विचलन ।
3. अच्छे परिक्षेपण के माप की विशेषताएँ (Features of a good measure of dispersion)- (i) श्रृंखला के सभी मदों पर आधारित, (ii) गणना सरल, (iii) समझने में सरल, (iv) निदर्शन में परिवर्तन का कम प्रभाव, (iv) उच्चस्तरीय अध्ययन के लिये इसका बीजगणितीय प्रयोग संभव ।
4. परिक्षेपण के उद्देश्य (Objectives of Dispersion)-(i) मध्यमानों की विश्वसनीयता की जाँच करना, (ii) विचरण को नियंत्रित करने में आधार का काम देना, (iii) दो या दो से अधिक श्रेणियों में तुलनात्मक अध्ययन करने में सहायक होना, (iv) श्रृंखला के गठन अथवा रचना के विषय में जानकारी देना ।
5. विस्तार (Range)-किसी एक समकमाला के सबसे बड़े और सबसे छोटे मूल के अन्तर को विस्तार कहे हैं। समीकरण के रूप में विस्तार-L-S.
6. चतुर्थक विचलन (Quartile Deviation)-तृतीयक चतुर्थक (Q1) तथा प्रथम चतुर्थक (Q1) के अन्तर के आधे अथवा औसत का चतुर्थक विचलन कहते हैं । सूत्र में, चतुर्थक विचलन Q.D.= Q3+01/2
7. चतुर्थक विचलन के गुण (Merits of Q.D.)-समझने में सरल, चरम मूल्यों से कम प्रभावित होता है।
8. चतुर्थक विचलन के दोष (Demerits of Q.D.)-(i) श्रेणी की रचना पर पूरा प्रकाश नहीं डालता । (ii) निदर्शनों के परिवर्तन से अधिक प्रभावित हाता है। बीजगणितीय, विधियों का प्रयोग नहीं किया जा सकता।
9. माध्य विलचन (Mean Deviation) यह एक ऐसा मूल्य है जो किसी श्रेणी के माध्य से विभिन्न मूल्यों के औसत को प्रकट करता है।
10. माध्य विचलन के गुण (Merits of Mean Deviation)-(i) इसकी गणना करना सरल है। (ii) यह सभी मूल्यों पर आधारित है। (iii) यह चरम सीमाओं से कम प्रभावित होता है।
11. माध्य विचलनों के दोष (Demerits of Mean Deviation)-(i) यह बीजगणितीय चिह्नों (+,-) की अवहेलना करता है । (ii) यह निश्चित (Exact) नहीं है, अत: तुलनीय नहीं है
12. प्रमाण विचलन (Standard Deviation)-यह किसी समंकमाला के समान्तर माध्य से किये गये उनके विभिन्न मूल्यों के विचलनों के वर्गों का वर्गमूल है।
13. प्रमाण विचलन के गुण (Merits of Standard Deviation)-(1) यह सभी मूल्यों पर आधारित है। (ii) यह स्पष्ट एवं निश्चित है। (iii) यह निर्देश में परिवर्तन से अधिक प्रभावित नहीं होता । (iv) इसमें माध्य विचलन की तरह (+) (-) चिन्हों की अवहेलना नहीं होता।
(v) यह परिक्षेपण का सबसे अच्छा माप है
14. प्रमाण विचलन के दोष (Demerits of Standard Deviation)-(i) इसकी गणना अपेक्षाकृत थोड़ी जटिल है । (ii) इसे समझना भी थोड़ा कठिन है । (iii) यह चरम सीमाओं को अधिक महत्त्व देता है।
15. विचरण गुणांक (Coefficient of Variation) =(प्रमाण विचलन/समान्तर माध्य)×100
16. लॉरेंज वक्र (Lorenz Curve)-यह परिपेक्षण को प्रदर्शित करने की एक बिन्दु-रेखीय विधि है।
पाठ्यपुस्तक एवं परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्नोत्तर
(Textbook and Other Important Questions for Examination)
अति लघु उत्तरीय प्रश्न
(Very Short Answer Type Questions)
प्रश्न 1. परिक्षेपण की माप कौन-सी श्रेणी की माध्य कहलाती है ?
उत्तर-द्वितीय श्रेणी की।
प्रश्न 2. परिक्षेपण के तीन प्रचलित मापों के नाम लिखिए।
उत्तर-(i) विस्तार, (ii) चतुर्थक विचलन, (iii) प्रमाण विचलन ।
प्रश्न 3. विस्तार (Range) किसे कहते हैं ?
उत्तर-विस्तार (R) अधिकतम मूल्य तथा न्यूनतम मूल्य में अन्तर है।
सूत्र के रूप में, R = H-L.
प्रश्न 4. किसी स्कूल में पाँच छात्रों के मासिक खर्च क्रमश: 12 रु०, 20 रु०, 5रु० ,40रु० और 62 रु० हैं, विस्तार (Range) ज्ञात कीजिए।
उत्तर-विस्तार = 62 रु०,-12 रु० = 50 रु०
प्रश्न 5. चतुर्थक विचलन (Quartile Deviation) क्या होता है ?
उत्तर-चतुर्थक विचलन किसी श्रेणी के तीसरे तथा पहले चतुर्थक के अन्तर का आधार है।
सूत्र के रूप में,
Q.D.=Q3-01/2
प्रश्न 6. कौन से परिक्षेपण के माप में विचलन चिह्नों (+ तथा- ) की उपेक्षा की जाती है ?
उत्तर-माध्य विचलन।
प्रश्न 7.माध्य विचलन (Mean Deviation) किसे कहते हैं ?
उत्तर-एक समंकमाला के किसी माध्य (समान्तर माध्य, माध्यिका या भूयिष्ठक) से निकाले गये विचलनों को जोड़ के समान्तर माध्य को माध्य विचलन कहते हैं |
प्रश्न 8. एक व्यक्तिगत श्रेणी में माध्य विचलन की गणना का सूत्र लिखिए।
उत्तर-माध्य विचलन (M.D.)= (Q.D.)=£f(d)/V
प्रश्न 9. माध्य विचलन प्रायः माध्यिका से ही नहीं लिए जाते हैं ?
उत्तर-माध्य विचलन माध्यिका से इसलिए लिये जाते हैं क्योंकि माध्यिका से लिए गये विचलना का योग न्यूनतम होता है
प्रश्न 10. व्यक्तिगत श्रेणी में प्रमाण विचलन (Standard Deviation) की गणना का सूत्र लिखिए।
उत्तर-प्रमाण विचलन (0) =√£(X-X)²/N
प्रश्न 11. प्रमाप विचलन सदैव किस माध्य से लिये जाते हैं ?
उत्तर-प्रमाप विचलन सदैव समान्तर माध्य से लिये जाते हैं क्योंकि इससे लिए गए विचलनों के वर्गों का योग न्यूनतम होता है।
प्रश्न 12. प्रसरण (Variance) से क्या अभिप्राय है?
उत्तर-प्रसरण (Variance) (प्रमाण विचलन)²
प्रश्न 13. यदि किसी आवृत्ति बंटन का प्रसरण(Variance) 100 है तो इसका प्रमाण विचलन क्या होगा?
उत्तर -प्रमाप विचलन (o) =√ 100 = 10
प्रश्न 14. पाँच संख्याओं 1,4,5,7 तथा 8 का प्रमाप विचलन 2,4,5 है। यदि प्रत्येक संख्या में 10 जोड़ दिया जाये, तो नया प्रमाप विचलन क्या होगा?
उत्तर-नया प्रमाण विचलन (ò) = 245
प्रश्न 15. यदि किसी श्रेणी का प्रमाप विचलन 5 है तो उसका प्रसरण (Varianc) कितना होगा?
उत्तर-प्रसरण (Variance) (5)²= 25
प्रश्न 16. विचरण गुणांक (Coefficient of Variation) क्या होता है ?
उत्तर-विचरण गुणांक (C.V.) =10/100 x100=10%
प्रश्न 17. किसी आवृत्ति वितरण का समान्तर माध्य 100 और प्रमाप विचलन 10 है, तो उसका विचरण गुणांक (Coefficient of Variation) निकालें।
उत्तर-विचरण गुणांक (C.V.) =10/100x 100 = 10%
प्रश्न 18. दो श्रेणियों A तथा B का विचरण गुणांक 20% तथा 10% है, कौन-सी श्रेणी सजातीय अथवा समरूप कहलायेगी ?
उत्तर-B श्रेणी समाजतीय अथवा समरूप कहलायेगी क्योंकि इसका विचरण गुणांक अपेक्षाकृत कम है।
प्रश्न 19 एक प्रसामान्य बंटन में x+30 के अन्तर्गत कितनी प्रतिशत मदें शामिल होती है ?
उत्तर-X-30ó= 99.37% मदें।
प्रश्न 20. परिक्षेपण का बिन्दुरेखीय माप कौन-सा है ?
उत्तर-लॉरेंज वक्र।
प्रश्न 21. लॉरेंज वक्र किस आर्थिक समस्या के अध्ययन के लिए उपयुक्त है ?
उत्तर-किसी देश की आय तथा सम्पत्ति में असमानताओं की समस्या का अध्ययन करने के लिए लॉरेंज वक्र बहुत उपयुक्त है।
प्रश्न 22. परिक्षेपण का कौन-सा माप दो श्रेणियों की तुलना के लिए अधिक उपयुक्त हैं?
उत्तर-विचरण गुणांक।
प्रश्न 23. विस्तार का प्रमुख दोष क्या है ?
उत्तर-यह केवल दो चरण मूल्यों पर आधारित है।
प्रश्न 24. प्रमाप विचलन (Standard Deviation) क्या है ?
उत्तर-प्रमाप विचलन समान्तर माध्य से लिये गए विचलन के वर्गों के समान्तर माध्य का वर्गमूल है।
प्रश्न 25. निम्न श्रृंखला का विस्तार गुणांक ज्ञात कीजिये-

L- 105-50
उत्तर-विस्तार गुणांक
L-s/L+s= 105- 50/105+50
55/155= 0.354
प्रश्न 26. यदि प्रमाप विचलन 9 है तो प्रसरण का क्या मूल्य होगा?
उत्तर-प्रसरण = ó²= 9×9= 81
प्रश्न 27. विस्तार गुणांक ज्ञात करने का सूत्र लिखें।
उत्तर-विस्तार गुणांक =L-s/L-s
प्रश्न 28. चतुर्थक विचलन (Quartile Deviation) निकालने का सूत्र लिखो।
उत्तर-Q.D.=Q3-Q1/2
प्रश्न 29. चतुर्थक विचलन का दूसरा नाम क्या है ?
उत्तर-चतुर्थक विचलन का दूसरा नाम अर्द्ध-अन्तर चतुर्थक (Semi-inter-quartile) है।
प्रश्न 30. सर्वप्रथम प्रसारण शब्द का प्रयोग किसने किया था?
उत्तर-आर.ए. फिशर ने।
प्रश्न 31. अच्छे परिक्षेपण के माप की दो विशेषतायें लिखें।
उत्तर-(i) अच्छा परिक्षेपण शृंखला के सभी मदों पर आधारित होता है ।
(ii) इसकी गणना सरल होनी चाहिये।
प्रश्न 32. परिक्षेपण के कोई दो उद्देश्य लिखें।
उत्तर-(i) श्रृंखला के गठन अथवा बनावट के विषय में जानकारी देना।
(ii) माध्य से प्रभावीपन को जाँचना।
प्रश्न 33. निम्न सूचनाओं के आधार पर विस्तार ज्ञात करें-
20, 30,40,50 तथा 200
उत्तर-विस्तार =200-20 = 180
प्रश्न 34. यदि प्रश्न 33 में यदि दिये गये आँकड़ों में 200 हटा दिया जाये तब विस्तार क्या होगा?
उत्तर-विस्तार = 50-20 = 30
प्रश्न 35. प्रश्न 33 में यदि 50 के स्थान पर यदि 150 कर दिया जाये, तब विस्तार क्या होगा?
उत्तर-विस्तार = 200-20 = 180
प्रश्न 36. खुले सिरे वाले वितरण से क्या अभिप्राय है ?
उत्तर-खुले सिरे वितरण से अभिप्राय उस वितरण से है जिसमें निम्नतम वर्ग की निम्न सीमा या उच्चतम वर्ग की उच्चतम सीमा या दोनों ही न दिये गये हों।
प्रश्न 37. उदाहरण से बतायें कि विस्तार अधिकतम सीमा मूल्य से प्रभावित होता है।
उत्तर-मान लो हम निम्न मूल्य लेते हैं।
10. 15, 20, 50
ऐसी अवस्था में विस्तार = 50-10 = 40
यदि अधिकतम सीमा का मूल्य 50 के स्थान पर 100 हो जाये तो ऐसी अवस्था में विस्तार
= 100-10 = 90 होगा।
इस प्रकार हम देखते हैं कि विस्तार उच्चतम सीमा के मूल्य से प्रभावित होता है।
प्रश्न 38. चतुर्थक विचलन का दूसरा नाम क्या है ?
उत्तर-चतुर्थक विचलन का दूसरा नाम अर्द्ध अन्तर चतुर्थक विस्तार (Semi-inter-Quartile Range) है।
प्रश्न 39. प्रमाप विचलन गुणांक का सूत्र लिखें।
उत्तर-प्रमाप विचलन गुणांक =ó/X
प्रश्न 40. विचरण गुणांक की गणना का सूत्र लिखें।
उत्तर-विचरण गुणांक (ó/X)x100
प्रश्न 41. निम्नलिखित सूचना के आधार पर विचरण गुणांक (C.V.) की गणना करें-
(i) प्रतिदिन प्रति व्यक्ति में मजदूरी के आधार पर विचरण = 9 रुपए
(ii) औसत मजदूरी= 120
(iii) मजदूरों की संख्या = 500
उत्तर-C.F =(ó/X)×100
=√9/120×100= (3/120)×100=2.5%
प्रश्न 42. विच्छन श्रेणी से प्रमाप विचलन की गणना की विभिन्न विधियाँ लिखें।
उत्तर-विच्छन श्रेणी से प्रमाप विचलन की गणना की विधियाँ हैं-(i) वास्तविक माध्य विधि,(ii) काल्पनिक माध्य विधि, (iii) प्रत्यक्ष विधि तथा (iv) पद विचलन विधि ।
प्रश्न 43. निरपेश्य तथा सापेक्ष परिक्षेपण में क्या अंतर है ?
उत्तर-निरपेक्ष परिक्षपण को उन्हीं इकाइयों में व्यक्त किया जाता है जिनमें समंक होते हैं(जैसे रुपये, कि. ग्राम)। इसके विपरीत सापेक्ष परिक्षेपण प्रतिशत में या निरपेक्ष परिक्षेपण के गुणांक में व्यक्त किया जाता है।
प्रश्न 44. एक कार्यालय में 10 व्यक्तियों का मध्यमान वेतन 5400 रुपये है। उनमें से एक कर्मचारी का वेतन 6000 रुपये है । बतायें कि इस व्यक्ति के वेतन का विचलन धनात्मक है या ऋणात्मक।
उत्तर-उस व्यक्ति के वेतन का विलचन धनात्मक है।
प्रश्न 45. परिक्षेपण का कौन-सा माप सर्वोत्तम है और कैसे?
उत्तर-प्रमाप विचलन परिक्षेपण का सबसे अच्छा माप है क्योंकि इसमें अच्छे परिक्षेपण की लगभग सभी विशेषताएँ पाई जाती हैं।
प्रश्न 46. परिक्षेपण के कुछ माप मानों के प्रसरण पर निर्भर करते हैं लेकिन कुछ केन्द्रीय मान से मानों के विचरण को परिकलित करते हैं । क्या आप सहमत हैं ?
उत्तर-हाँ, हम इस बात से पूर्णत: सहमत हैं।
प्रश्न 47. परिक्षेपण के कौन से माप मूल्यों के विस्तार पर निर्भर करते हैं ?
उत्तर-विस्तार तथा चतुर्थक विचलन मूल्यों के विस्तार पर निर्भर करते हैं।
प्रश्न 48. परिक्षेपण के कौन से माप मध्यमान से विचलन मूल्यों पर आधारित हैं ?
उत्तर-माध्य विचलन तथा प्रमाप विचलन मध्यमान से विचलन मूल्यों पर आधारित हैं।
प्रश्न 49. परिक्षेपण के माप कितने प्रकार के हो सकते हैं ? उनके नाम लिखें।
उत्तर-परिपेक्षण माप दो प्रकार के हो सकते हैं-(i) निपरेक्ष तथा (ii) सापेक्ष ।
प्रश्न 50. प्रमाप विचलन का एक मुख्य दोष क्या है ?
उत्तर-इसे समझना एवं ज्ञात करना अपेक्षाकृत कठिन है ।
प्रश्न 51. परिक्षेपण के विभिन्न मापों के नाम बताएं।
उत्तर-(i) निरपेक्ष माप, (ii) सापेक्ष माप ।
प्रश्न 52. विस्तार का एक दोष लिखें।
उत्तर-वे श्रेणी के सभी मूल्यों पर आधारित नहीं हैं।
प्रश्न 53. कौन-सी परिक्षेपण की माप 50 प्रतिशत मूल्य से सम्बन्धित है ?
उत्तर-अन्तर चतुर्थक विस्तार ।
प्रश्न 54.विचरण क्या है ?
उत्तर-प्रमाप विचलन के वर्ग को विचरण कहते हैं।
समीकरण में, प्रसरण = ó²
प्रश्न 55. विचरण गुणांक ज्ञात करने का सूत्र लिखें।
उत्तर-C.V.=(ó/X)x100
प्रश्न 56. प्रमाप विचलन की एक बीजगणितीय विशेषता बताएँ।
उत्तर-समान्तर माध्य से लिये गये विचलन वर्गों का याग सदैव न्यूनतम होता है।
प्रश्न 57. सामूहिक प्रमाप विचलन ज्ञात करने का सूत्र लिखें।
N,( +DE) + Na(a +D)
उत्तर-ó 12 =√N1(ó²1+D²1)+N²(ó²2+D²2)/N¹+
प्रश्न 58. प्रमाप विचलन का दूसरा नाम क्या है ?
उत्तर-विचलन वर्ग माध्य मूल ।
लघु उत्तरी प्रश्न
(Short Answer Type Questions)
प्रश्न 1. परिक्षेपण किसे कहते हैं ? निरपेक्ष परिक्षेपण के चार प्रचलित मापों के नाम लिखें।
उत्तर-परिक्षेपण से अभिप्राय समंकमाला में विभिन्न मूल्यों के विस्तार, दूरी तथा विखराव से होता है । बऊले के अनुसार, “परिक्षेपण पदों क विचरण या अन्तर का माप है। परिक्षेपण की सहायता से मदों के केन्द्रीय प्रवृत्ति से विचलन ज्ञात किये जाते है।”
निरपेक्ष परिक्षण के चार प्रचलित माप-(i) विस्तार, (ii) चतुर्थक विचलन, (iii) माध्य विचलन, (iv) प्रमाप विचलन इत्यादि हैं।
प्रश्न 2. प्रमाप विलचन का क्या अर्थ है ? इसको किस चिह्न द्वारा दर्शाया जाता है ?
(What is Standard Deviation ? Give its marks.)
उत्तर-किसी श्रेणी के समानान्तर माध्य के विचलनों के वर्गों के समानान्तर माध्य का वर्गमूल प्रमाप विचलन कहलाता है। प्रमाप विचलन के माप के लिए ग्रीक वर्णमाला का अक्षर ó सिग्मा (Small Sigma) प्रयुक्त किया जाता है। सूत्र के रूप में,
ó=√£(X-X)²/N
प्रश्न 3. विस्तार तथा चतुर्थक विचलन क्या हैं ? इसकी गणना का सूत्र दीजिए।
उत्तर-विस्तार परिक्षेपण का सरल माप है। किसी श्रेणी के सबसे बड़े और सबसे छोटे मूल्य के अन्तर को विस्तार कहते हैं। इसकी गणना के लिए निम्न सूत्र का प्रयोग किया जाता है-
विस्तार = R=L-S
चतुर्थक विचलन को अर्द्ध अन्तर चतुर्थक विस्तार भी कहते हैं। परिक्षेपण का यह माप श्रृंखला के तृतीय चतुर्थक और प्रथम चतुर्थक के मूल्यों पर आधारित है। इसकी गणना करने के लिये निम्नलिखित सूत्र का प्रयोग किया जाता है।
चतुर्थक विचलन Q.D.=Q3-Q1/2
प्रश्न 4. निरपेक्ष और सापेक्ष परिक्षेपण में क्या अंतर है?
उत्तर-जब किसी समंकमाला के विस्तार, बिखराव या विचरण का माप निरपेक्ष रूप में उसकी इकाई द्वारा ज्ञात किया जाता है, तो उसे परिक्षेपण का निरपेक्ष माप कहते हैं और जब परिक्षेपण के निरपेक्ष माप को संबंधित माध्य से भाग दे देते हैं और इस प्रकार जो अनुपात या प्रतिशत प्राप्त होता है, उसे परिक्षेपण का सापेक्ष माप कहते हैं।
प्रश्न 5. परिक्षेपण के आदर्श माप के कोई तीन गुण बताओ।
उत्तर-(i) आदर्श परिक्षेपण का माप स्पष्ट एवं सरल होता है।
(ii) यह सभी मूल्यों पर आधारित होता है।
(iii) निदर्शन में परिवर्तनों का परिक्षेपण के आदर्श माप पर अधिक प्रभाव नहीं पड़ता।
प्रश्न 6. माध्य विचलन (Mean Deviation) और प्रमाप विचलन (Standard Deviation) में अंतर बताइये।
उत्तर-(i) माध्य विचलन में श्रेणी के मूल्यों में विचलन किसी भी सांख्यिकी माध्य (सामानान्तर माध्य, माध्यिका या बहुलक) से निकाले जा सकते हैं जबकि प्रमाप विचलनों में श्रेष्ठ के मूल्यों के विचलन सदैव सामानान्तर माध्य से लिये जाते हैं।
(ii) माध्य विचलन निकालते समय बीजगतिणतीय चिहों (+व-) को छोड़ दिया जाता है जबकि प्रमाप विचलन निकालते समय बीजगणितीय चिह्नों (+व-) को छोड़ा नहीं जाता बल्कि उनका वर्ग कर लिया जाता है।
प्रश्न 7.एक कस्बे में 25% लोग 45,000 रुपये से अधिक आय अर्जित करते हैं जबकि 75% लोग 18,000 से अधिक अर्जित करते हैं। परिक्षेपण के निरपेक्ष एवं सापेक्ष मानों का परिकलन कीजिये।
(In a town 25% of the person eamed more than 45,000 whereas 75% earned more than Rs.18,000.Calculate the absolute and relative measure of dispersion.)
उत्तर-(i) परिक्षेपण का सापेक्ष मान अर्थात् चतुर्थक विचलन
= Q3-Q1/2=45,000-18,000/2 =13,500 रूपये
(ii) परिक्षेपण का सापेक्ष मान अर्थात् चतुर्थक विचलन का गुणांक
=Q3-Q1/Q3+Q1 =45,000-18,000/45,000+18,000
= 27,000/63,000
=0.428
प्रश्न 8. मूल तथा पैमाने में परिवर्तन करने पर प्रमाप विचलन, माध्य तथा विवरण पर क्या प्रभाव पड़ेगा?
What will be the effect of change of origin and change of scale on the standard deviatiobn, mean and variance ?
उत्तर-(i) मूल में परिवर्तन करने पर प्रमाप विचलन में कोई परिवर्तन नहीं होगा परन्तु मूल में परिवर्तन आने पर माध्य पर प्रभाव पड़ेगा।
(ii) पैमाने में परिवर्तन करने पर माध्य, प्रमाप विचलन तथा विचरण में परिवर्तन आयेगा।
प्रश्न 9. 10 मानों का योग 100 है और उनके वर्गों का योग 1090 है । विचरण गुणांक ज्ञात कीजिये।
(The sum of 10valuesis 100 and the sum of then squaresis1090. Find the coefficient of variance.)
उत्तर-प्रमाप विचलन ó =√£x³/N – (X)²
अथवा, ó²=£x²/N -(X) =1090/10-(10)²
=109-100=9
अथवा, ó=√9=3
अत: विचरण गुणाक = ó/X×(100)=3/10 x 100 = 300
प्रश्न 10. प्रमाप विचलन को विचलन का वर्गों के माध्य मूल भी क्यों कहा जाता है?
(Why is standard deviation also known as the root mean square deviation ?)
उत्तर-प्रमाप विचलन को विचलन के वर्गों का माश्य मूल भी इसलिये कहा जाता है क्योंकि यह माध्य के विचलनों के वर्गों के माध्य का मूल है। प्रमाप विचलन की गणना में हम पहले माध्य की गणना करते हैं फिर माध्य से मदों विचलन ज्ञात किया जाता फिर विचलनों का वर्ग निकालकर उसका योगफल निकाला जाता है। विचलन के वर्गों के जोड़ को मदों की संख्या से विभाजित किया जाता है और जो परिणाम आता है उसका वर्गमूल ज्ञात किया जाता है प्रमाप विचलन का चिह्न है। सूत्र रूप में
ó= √£(X-X)²/N
प्रश्न 11. पूर्ववर्ती प्रश्न में विचरण के सापेक्ष मापों का परिकलन कीजिए और वह मान बताएं जो आपके विचार में सर्वधिक विश्वसनीय है।
उत्तर-परास का कोण सापेक्ष माप है परास गुणांक । अतः हम परास गुणांक की गणना करेंगे।
(i) गेहूँ का परास गुणांक
=L-S/L-S =25-9 /25+9=16/36=0.44
(ii) चावल का परास गुणांक
=L-S/L-S = 34-12/34+12 =22/43=0.47
इसी प्रकार दोनों फसलों की उपजों के चतुर्थक विचलन गुणांक तथा विचरण गुणांक ज्ञात किए जाएंगे।
प्रश्न 12. एक कारखाने में 50 मजदूरों की औसत दैनिक मजदूरी 200 रुपये है तथा मानक विचलन 40 रुपये था । प्रत्येक मजदूर की मजदूरी में 20 रुपये की वृद्धि की गई, अब मजदूरों की औसत मजदूरी एवं मानक विचलन क्या है ? क्या मजदूरी में समानता आई?
उत्तर-प्रत्येक मजदूर की मजदूरी में वृद्धि = 20 रुपये
मजदूरी वृद्धि से पूर्व कुल मजदूरी का योगफल = 10,000 + 1,000 = 11,000 रुपये
नई औसत मजदूरी=£X/N=11000/50 = 220
अत: नई औसत मजदूरी = 220 रुपये
औसत मजदूरी में परिवर्तन होगा, परन्तु मानक विचलन में कोई परिवर्तन नहीं आएगा।
अब मजदूरी में समानता ज्ञात करने के लिए विचरणता गुणांक ज्ञात करेंगे।
आरम्भ में C.V.(ó/X)x100= 40/200 = 100=20%
बाद में C.V.(ó/X)x100= 40/220 ×100= 18.18%
अब मजदूरी में अधिक समानता आ गई है क्योंकि विचरण गुणांक कम हो गया है।
प्रश्न 13. पूर्ववर्ती प्रश्न में यदि प्रत्येक मजदूरी में 10% की वृद्धि की जाये तो माध्य और मानक विचलन पर क्या प्रभाव पड़ेगा?
उत्तर-प्रत्येक मजदूर की मजदूरी में 10% की वृद्धि करने पर नया माध्य 200 रुपये (200 + 20) होगा।
मानक विचलन पर कोई प्रभाव नहीं पड़ेगा।
दीर्घ उत्तरीय प्रश्न
(Long Answer Type Questions)
प्रश्न 1. एक विशेष वितरण में चतुर्थ विचलन 15 अंक है और चतुर्थ विचलन का गुणांक 0.6 है । Q1 तथा Q3 ज्ञात करें।
उत्तर-माध्य विचलन (Q.D) =Q3-Q1/2=15 अंक
अथवा,Q3-Q1 = 30
माध्य विचलन का गुणांक = Q3-Q1/Q3-Q1=0.6
30/Q3+Q1=0.6
अथवा, Q3-Q1 =30/0.6
Q3+Q1 = 50
(i) तथा (ii) को जोड़ने पर 23-01 = 30
(Q3 – Q1 = 30)+(Q3 +Q1= 50)=2Q3=80
Q1=40 अंक
Q3-Q1 = 30
-Q1=30-Q3
अत:
-Q1=30-40=-10
Q1=10
Q1=10 अंक तथा Q3 = 30 अंक उत्तर ।
प्रश्न 2. किमी क्रिकेट टीम के लिए एक बल्लेबाज का चयन करना है । यह चयन X और Y के बीच पाँच पूर्ववर्ती स्कोर के आधार पर करना है, जो निम्नवत् है
X 25 85 40 80 120
Y 50 70 65 45 80
किस बल्लेबाज को टीम में चुना जाना चाहिये?
(क) अधिक स्कोर बनाने वाले को या
(ख) अधिक भरोसेमंद बल्लेबाज को।
A batsman is to be selected for a cricket team choice between X and Y on the basis of their five perevious score which are :
(a) Which batsman should be selected of we want?
(b) A more reliable batsman in the team.
उत्तर-Xबल्लेबाज का स्कोर (Score of x batsman):-

माध्य (AM) =Σx/N =350/5= 70
औसत स्कोर = 70 रन
प्रमाप विचलन (Ó) =√ΣX²)N=√5750/5 =√1150
=33.91 रन (स्कोर)
प्रमाप विचलन का गुणाक= ó/X =33.91/70= 0.484
विचरण (Variance)=£(X-X)/N= £x²/N
=5750\5
= 1150 रन
विचरण का गुणांक (CV) =ó/X=(33.91/70)48 44%
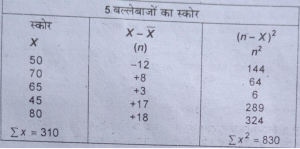
X=£x/N= 310/5= 62
औसत स्कोर = 62 रन
Ó=√£X²/N =√830/5=√166= 12.88 रन
प्रमाण विचलन का गुणांक= Ó/N=12.88/62=0.207
विचरण अथवा Ó²=£x²/N=830/5=166 रन
विचरण का गुणांक=(Ó/X)×100=(12.88/62)×
= 20.77%
निष्कर्ष (Conclusion)-(i) x बल्लेबाज को चुना जाना चाहिये क्योंकि उसका औसत स्कोर (70 रन) y बल्लेबाज के औसत स्कोर (62 रन) से अधिक है।
(ii) y बल्लेबाज अधिक भरोसेमंद (विश्वसनीय) है क्योंकि उसका विचरण गुणांक (C.V=20.77%) X बल्लेबाज का विचरण गुणांक (48 44%) से कम है।
प्रश्न 3. दो ब्राण्डों के बल्ब की गुणवत्ता जाँचने के लिये ज्वलन अवधि घंटों में उनके जीवनकाल को प्रत्येक ब्राण्ड के 100 बल्बों के आधार पर निम्नानुसार अनुमानित किया गया है-
(To check the quality of two brands of light bulbs, their life in burning hours was estimated as under for 100 bulbs of each brand.)

(क) किस ब्राण्ड का जीवन काल अधिक है?
(Which brand gives higher life ?)
(ख) कौन-सा ब्राण्ड अधिक भरोसेमंद है ?
(Which brand is more dependable ?)
उत्तर-ब्राण्ड ‘क’ बल्ब

विचरण गुणांक की गणना (Calculation of co-efficient of Variation)
S.D. =√£fd²/N-(fd+/N)²×C
=√193/100-(19/100)²×50 =√1.93-(0.19)²
=√1.8939×50=1.376×50=68.8 घंटे
माध्य (X) = A+ £fd/N×C =125+19/W×50
= 125 + (0.19 x 50) = 125 +9.5 = 134.5 घंटे
C.V=Ó/X × 100= 68.8/134 x 100 = 51.15

A.M.=125
विचरण गुणांक की गणना (Calculation of co-effeccient of Variation)
S.D=√£fd²/N-(fd/N)²×C =√161/100-(23/100)²×50
√0.61-(0.23)²×50
=√0.61-0.0529×50
√0.5571×50= 0.746×50 = 37.32 घंटे
माध्य (X) = A + £fd/N ×C =125+23/100×50
= 125+ (0.23 x 50)
= 125 + 11.5 = 136.5
विचरण गुणांक (C.V) = Ó/X = 37.2/136.5=27.34%
निष्कर्ष (Conclusion)-(i) ‘ख’ ब्राण्ड बल्ब का जीवन काल अधिक है क्योंकि बल्ब ‘ख’ का माध्य जीवन काल बल्ब ‘क’ बल्ब के माध्य जीवन काल से अधिक है।
(ii) ‘ख’ ब्राण्ड बल्ब अधिक भरोसेमंद है क्योंकि इस बल्ब के इस ब्राण्ड का विचरण गुणांक ‘क’ ब्राण्ड के बल्ब के विचरण गुणांक से कम है।
प्रश्न 4.11 मनुष्यों की ऊँचाई 61, 64, 68, 67,68, 66, 70, 65, 67 तथा 72 इंच है।
विस्तार ज्ञात कीजिए। यदि सबसे छोटे कद वाले व्यक्ति को हटा दिया जाये तब विस्तार में कितने प्रतिशत परिवर्तन होगा?
(The height of 11 men were 61, 64, 68, 69, 67, 68, 66, 70,65, 67,72 inches. Calculate the range of the shortest men is emitted, what is the percentage change in the range ?)
उत्तर-(i) विस्तार = L-S = 72-61 = 11 इंच
(ii) नया विस्तार (सबसे छोटे आदमी को हटाने के पश्चात् = 72 -64 = 8 इंच
(iii) विस्तार में परिवर्तन = 11-8 = 3 इंच ।
विस्तार में प्रतिशत परिवर्तन = 3/11×100 = 27.2%
प्रश्न 5. निम्न तालिका में 100 व्यक्तियों की ऊंचाई दी गई है। विस्तार विधि से परिक्षेपण ज्ञात करें।
(The following table gives you the height of 100 person.Calculate disperson by range method.)

विस्तार =L-s = 170-161=S
विस्तार का गुणांक =L-S/L+S= 170-161/170+161=9/331=0.3
प्रश्न 6. सिद्ध कीजिये कि माध्य विचलन सभी मानों पर आधारित होता है। अत: एक भी मान में परिवर्तन इस पर प्रभाव डालेगा।
उत्तर-प्रश्न में दिये गये कथन को सिद्ध करने के लिये हम निम्नलिखित मान लेत हैं और उनका माध्य विचलन ज्ञात करते हैं।
2.4.7.8.9

माध्य (X)= £X/N=30/5=6
माध्य विचलन =£D/N=15/5=2.4
अब हम एक मान बदल देते हैं। 9 के स्थान पर 14 लते हैं।

X= £X/N=35/5=7
माध्य विचलन =£D/N=16/5=3.2
इस प्रकार हम देखते हैं कि मान के बदलने से माध्य विचलन में में अंतर आ गया है। पहले माध्य विचलन 24 मान बदलने के बाद यह 3.2 हो गया है।
प्रश्न 7.सिद्ध करें कि यदि माध्य विचलन माध्य से परिकलित किया जाये तो यह अधिक होगा और यदि इसे मध्यिका से परिकलित किया जाये तो यह निम्नतम होगा।
उत्तर-प्रश्न में दिये गये कथन को सिद्ध करने के लिये हम निम्नलिखित मान लेते हैं और उनसे माध्य विचलन तथा मध्यिका से माध्य विचलन की गणना करते हैं:
2,4,7,8,9
माध्य से माध्य विचलन की गणना
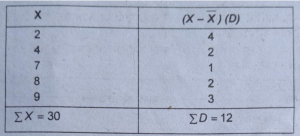
X= £X/N=30/5=6
माध्य से माध्य विचलन =£D/N=12\5=2.4
माध्य से माध्य विचलन की गणना
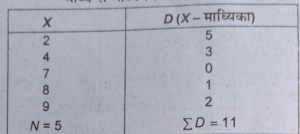
माध्य=N+1/2 वें मद का मूल्य =5+1/2
= तीसरे मद का मूल्य =7
माध्य विचलन =£D/N=11/5=2.2
माध्य से विचलन 2.4है और मध्यिका से माध्य विचलन 2.2 है। अत: सिद्ध हुआ’ कि मध्यिका से माध्य विचलन माध्य से माध्य विचलन से कम होता है।
प्रश्न 8. इंचों में मापा गया ऊँचाई का प्रमाप विचलन व्यक्ति के उसी समूह में फुटों में मापे गये ऊँचाई के प्रमाप विचलन से अधिक होगा।
(The standard deviation of height measured in inches will be larger than the standard deviation of heights measured in feet for the same group of individuals. Comment on the validity, or, otherwise of this statement with appropriate explanation.)
उत्तर-यह कथन पूर्णतः सत्य है। इसका कारण यह है कि प्रमाप विचलन निरपेक्ष माप है। यह माप कठिनाई उत्पन्न कर सकता है, जब माप की इकाइयाँ भिन-भिन्न होती हैं। माप इकाई जितनी कम होती जायेगी, प्रमाप विचलन भी उतना ही अधिक बढ़ता जायेगा और माप इकाई जितनी अधिक होती जायेगी, प्रमाप विचलन भी उतना ही कम होता जायेगा। उदाहरण के लिये हम रुपयों के स्थान पर पैसों में आय की गणना करते हैं तो प्रमाप विचलन 100 गुणा बढ़ जायेगा। प्रमाप विचलन में बढ़ोत्तरी बारह गुना होगी। (1 फुट = 12 इंच) इसे हम उदाहरण द्वारा समझा सकते हैं। मान लो 5 वस्तुओं की ऊँचाई नीचे फुटों में दी गई है। इसका हम प्रमाप विचलन ज्ञात करेंगे।

अब हम इन्हीं ऊँचाई को इंचों में लेकर प्रमाप विचलन ज्ञात करेंगे।
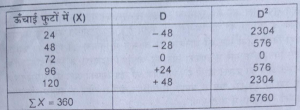
इस तरह हम देखते हैं कि प्रमाप विचलन 12 गुणा बढ़ गया 1
प्रश्न 9. किसी बारम्बारता वितरण को समझने में परिक्षेपण का माप केन्द्रीय मान का एक अच्छा संपूरक है, टिप्पणी लिखें।
(A measure of dispersion is a good supplement to the central value in understanding a frequencey distribution.’ Conment.)
उत्तर-परिक्षेपण का माप केन्द्रीय माप का एक संपूरक (Ameasure of dispersion a good supplement to the central value): परिक्षेपण का माप किसी बारम्बारता वितरण को समझने में केन्द्रीय माप का एक अच्छा संपूरक है। केन्द्रीय माप वितरण केवल पहले के बारे
में बताता है। यह मान आँकड़ों में विद्यमान परिवर्तनशीलता को नहीं दर्शाता । उदाहरण के लिये
यदि 10 विद्यार्थियों के समूह के औसत अंक 60 हैं तो इससे यह अनुमान अवश्य लगाया जा सकता है कि औसत रूप में विद्यार्थियों का स्तर कैसा है, परन्तु इससे यह बिल्कुल पता नहीं चलता कि 10 विद्यार्थियों के अंकों में परस्पर कितना अंतर है। सभी के अंक 60 हैं या कुछ एक के बहुत अधिक हैं और कुछ के बहुत कम है। इसी बात का स्पष्टीकरण एक और उदाहरण लेकर किया जा सकता है। नीचे राम, रहीम और मारिया के परिवारों की आय के आँकड़े दिये गये हैं। राम के परिवार में चार सदस्य हैं। रहीम के परिवार में 6 सदस्य हैं और मारिया के परिवार में 5 सदस्य हैं।
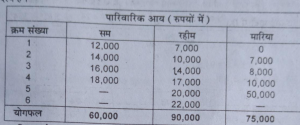
तालिका से पता चलता है कि प्रत्येक परिवार की औसत आय 15000 रुपये
60,000/4, 90.000/5 तथा 75,000/5 है परन्तु व्यक्तिगत आय में बहुत भिन्नताएँ हैं। अत: यह स्पष्ट है कि औसत वितरण केवल एक पहलू के बारे में बताता है अर्थात् मानों का प्रतिनिधि आकार इसे बेहतर ढंग से समझने के लिये हमें मानों के प्रसार की आवश्यकता है। राम के परिवार में
आय की भिन्नता अपेक्षाकृत कम है । रहीम के परिवार में आय की यह भिन्नता काफी अधिक है, जबकि मारिया के परिवार की यह भिन्नता अधिकतम है। केवल औसत का ज्ञान अपर्याप्त है। यदि आपको किसी अन्य मान की जानकारी हो जो मान में वितरण की मात्रा को प्रदर्शित करता है तो उस वितरण के बारे में आपका ज्ञान बढ़ जायेगा। उदाहरण के लिये प्रति व्यक्ति आय केवल औसत आय का प्रदर्शन करती है। परिक्षेपण की माप आपको आय की असमानताओं के बारे में बता सकती है। इस तरह से समाज के विभिन्न वर्गों में लोगों के सापेक्ष जीवनस्तर के बारे में आपकी जानकारी में वृद्धि होगी।
प्रश्न 10. निम्नलिखित वितरण के लिये माध्य से माध्य विचलन और मानक विचलन
का परिकलन कीजिये । (Calculate the mean deviation about mean and standard deviation for the following distribution):
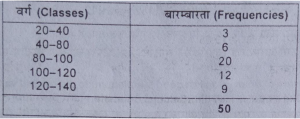
उत्तर-माध्य से माध्य विचलन और मानक विचलन की गणना (Calculation of mean and standard deviation)-
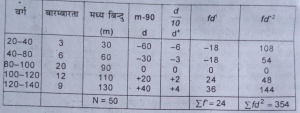
माध्य X=A+£fd/N×c
= 90 + 24/50 × 10
=90+4.8 = 94.80
अत: माध्य 94.8 अंक
माध्य विचलन (Ó) =√£fd²/N-(£fd)²×C
=√354/50-(24/50)²×10
√70.08-0.23×100
=√6.85×10
=26.7×10 =26.17
अत: माध्य विचलन = 26.17 अंक
मध्यिका से माध्य विचलन की गणना (Calculation mean deviation about mean)
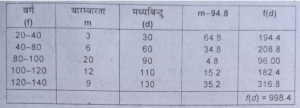
माध्य विचलन=£f|d|/N=998.4/50 = 19.68
अत: माध्य विचलन = 19.68
माध्य विचलन= f|d|/N=998.4/50 = 19.968
प्रमाप विचलन की गणना (Calculation of Standard Deviation)
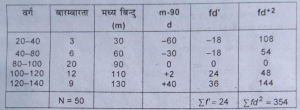
कल्पित माध्य = 90
प्रमाप विचलन= √£fd²/N -(£fd/N)²×C
=√354/50-(24/50)²×10
=√7.08-0.23×10
=√6.85×10=26.17
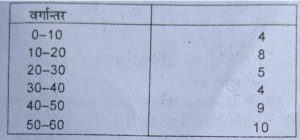
प्रश्न 11. निम्नलिखित आवृत्ति वितरण से निम्न चतुर्थक (Q1), तृतीय चतुर्थक (Q) की गणना करें:
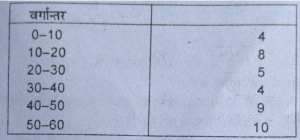
प्रश्न 12. फामें में एक क्विंटल गेहूँ की उत्पादन लागत का वितरण (रुपयों) में निम्नलिखित है (The distribution of the cost of production (in rupees) of a quintal of wheat in 50 farms is a follows):
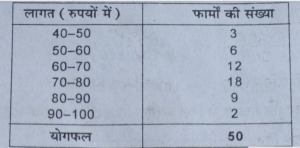
(क) विचरण ज्ञात करें:
(i) प्रत्यक्ष विधि से (ii) पद-विचलन विधि से
तथा परिणामों को समान्तर माध्य से और माध्य विचलन से तुलना करें।
(ख) विचरण गुणांक की गणना करें :
(i) मूल्यों के प्रमाप विचलन से (ii) समान्तर माध्य से, माध्य विचलन से तथा दोनों की तुलना करें। लागतों में विचरण से आप किस निष्कर्ष पर पहुंचते हैं ?
उत्तर-प्रत्यक्ष विधि से विचरण की गणना-
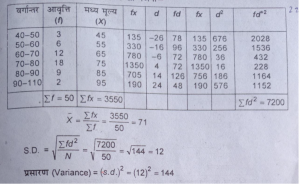
पद विचलन से विचरण की गणना

A.M.= 75
Ó=√fd²/Σf -(Σfd/Σf)²×1 =√80/50-(-20/50)×1
=√1.60-0.16×10 =√1.44×10= 1.2×10=12
विचरण =Ó (12)²-144
विचरण गुणांक की गणना-
(i) विचरण गुणांक (प्रमाप विचलन से)
=Ó/X=12/71= 0.169 या 0.17 लगभग
(ii) विचरण गुणांक (माध्य विचलन से)
=MD/X =492/50/50=9.84/71= 0.138= 0.14 लगभग
निष्कर्ष : दो परिणाम में आपस में तुलना करने पर हम कह सकते हैं कि माध्य विचलन को तुलना में प्रमाप विचलन में विचरण गुणांक अधिक है।
प्रश्न 13 निम्नलिखित विधियों से नीचे दी गई तालिका से प्रमाप विचलन ज्ञात करें।
(Calculate standard deviation from the following table)
(i) वास्तविक माध्य विधि (Actual Mean Method)
(ii) काल्पनिक माध्य विधि (Assumed Mean Method)
(iii) पद विचलन विधि (Step Deviation Method)
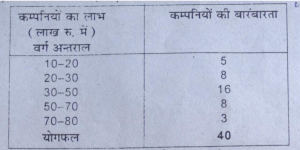
(1) वास्तविक माध्य विधि द्वारा प्रमाप विचलन की गणना (Calculation of S.D. with the help of Actual Mean Method)

X=√Σfm\ Σf= 1620/40 = 40.5
Ó=√Σfd²/N= √11790/40= 17.168
(2) कल्पित माध्य विधि से प्रमाप विचलन की गणना (Calculation of Standard Deviation by Assumed Mean Method)
हमने यहाँ कल्पित माध्य 40 लिया है।
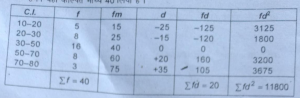
Ó=√£fd²/N -(fd/N)²
=√11800/40-(20/40)²= √294.75= 17.168
(3) पद विचलन विधि से प्रमाप विचलन की गणना (Calculation ofS.D. by step Deviation Method)
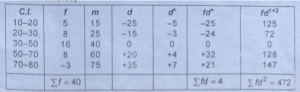
कल्पित माध्य =40
प्रमाप विचलन (Ó) =√£fd²/£f-(fd¹/£f)×C
=√472/40-(4/40)×5
=√11.8-0.1×5
=√11.79×5 =17.168
प्रश्न 14.लारेंज वक्र के निर्माण में निहित चरण लिखें।
(Write down the steps involved in the construction of a Lorenz Curve.)
उत्तर-लारेंज वक्र के निर्माण में निम्नलिखित चरण निहित हैं-
(i) वर्गों के मध्य बिन्दु परिकल्पित करें तथा उनका संचयी योग पता लगाएँ।
(ii) संचयी योग को प्रतिशत में बदलें।
(iii) बारम्बारता को जोड़ें तथा संचयी बारम्बारता प्राप्त करें।
(iv) संचयी बारम्बारता को प्रतिशत में बदलें।
(v) अब ग्राफ पेपर पर चर के संचयी प्रतिशत को y अक्ष पर तथा बारम्बारता के संचयो प्रतिशत को x अक्ष पर प्रदर्शित करें। इस तरह से प्रत्येक अक्ष पर 0 से 100 तक का मान होगा।
(vi) निर्देशांक (0.0) को (100, 100) से जोड़ते हुए एक रेखा खींचे । इसे समवितरण रेखा कहा जाता है।
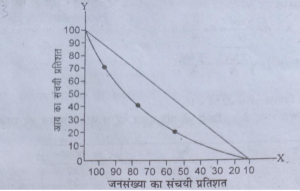
(vii) चर के संचयी प्रतिशत को बारम्बारता के संगत संचयी प्रतिशत के साथ अभिलेखित करें । इन बिन्दुओं को मिलाकर एक वक्र प्राप्त करें। आगे लारेंज वक्र का ग्राफ दिया गया।

प्रश्न 15. नीचे एक कम्पनी के कर्मचारियों की मासिक आय दी गई है। इसकी सहायता एक लारेंज वक्र बनायें।
(Give below at the monthly incomes of employees of a company.)

उत्तर-

प्रश्न 16. नीचे तालिका की सहायता से लारेंज वक्र बनायें।
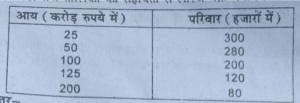
उत्तर-

प्रश्न 17. निम्न समंकमाला का प्रसारण (62) तथा प्रमाप विचलन प्रत्यक्ष तथा अप्रत्यक्ष विधि द्वारा ज्ञात कीजिए। दोनों विधियों का प्रयोग कीजिए।
उत्तर-(क) प्रत्यक्ष विधि द्वारा (Direct Method) :
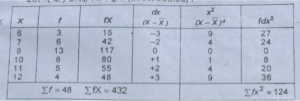
(i)X=£fx/N =432/N=9
(ii)(Ó²)=£fx²/N=124/48=258
(iii) विचरण (Ó) = √विचरण =√2.58 = 1.6
लघु विधि द्वारा (B) Indirect Method) :

AM=9
(i) X= A+ΣdX/N=9+ó/N =9
(ii) विचरण (Ó²)=√£fdx²/N-£fdx/N
(iii) प्रमाप विचरण (Ó) = √2.58 = 1.6
प्रश्न 18. एक राज्य के 10 जिलों की प्रति एकड़ गेहूँ व चावल फसल की उपज निम्नवत् है-
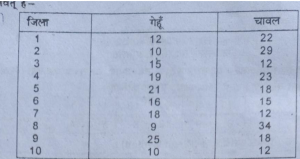
प्रत्येक फसल के लिए परिकलन करें-(क) परास, (ख) चतुर्थक विचलन, (ग) माध्य से विचलन, (घ) माध्यम से माध्य विचलन, (ङ) मानक विचलन, (च) सिक फसल में अधिक विचरण है, (छ) प्रत्येक फसल के लिए विभिन्न मापों की तुलना कीजिए ।
उत्तर-गेहूँ की फसल-
(क) परास: 1-S=25-9 = 16
(ख) चतुर्थक विचलन :Q3-Q1/2
Q1=3(N+1)/4 वें मद का मूल्य
=3×11\4=33\4=8.25 वें मद का मूल्य
इसी प्रकार Q1 का मूल्य ज्ञात करें और ऊपर दिए गए सूत्र का प्रयोग करके चतुर्थक विचलन ज्ञात करें।
(ग) पहले माध्य निकालें और प्रत्येक मद का माध्य से विचलन ज्ञात करके उनका नोगफल निकालें। योगफल को 10 से विभाजित करें।
(घ) पहले माध्यिका का ज्ञात करें । प्रत्येक मद का मध्यिका से विचलन ज्ञात करें। उसे जोड़ें तथा योगफल को 10 से भाग दें।
(च) विद्यार्थी स्वयं करें।
(छ) विद्यार्थी स्वयं करें।
चावल की फसल
(क) परास : 1-S=34-12 = 22
(ख) चतुर्थक विचलन :Q3-Q1/2
Q3=3(10+1)/4 वें मद का मूल्य
=3×11/4= 33/4=8.25 वें मद का मूल्य
इसी प्रकार २५ का मूल्य ज्ञात करें और ऊपर दिए गए सूत्र का प्रयोग करके चतुर्थक विचलन ज्ञात करें।
(ग) पहले माध्य निकालें और प्रत्येक मद का माध्य से विचलन ज्ञात करके उनका योगफल निकालें। योगफल को 10 से भाग दें।
(घ) पहले माध्यिका का ज्ञात करें। प्रत्येक मद का माध्यिका से विचलन ज्ञात करें और उसका योगफल ज्ञात करें और योगफल को 10 से विभाजित करें।
(च) विद्यार्थी स्वयं करें।
(छ) विद्यार्थी स्वयं करें।
प्रश्न 19. परिक्षेपण के वैकल्पिक मापों की तुलनात्मक विशेषताएँ लिखें।
(Write down the comparative features of alternative) measures of dispersion.)
उत्तर-परिक्षेपण के वैकल्पिक मापों की तुलनात्मक विशेषताएँ निम्नलिखित हैं-
(i) कठोरता से परिभाषित (Rigidly defined)-परिक्षेपण के चारों प्रमाण-विस्तार, चतुर्थक विचलन, माध्य विचलन तथ प्रमाप विचलन को कठोरता से परिभाषित किया जाता है।
(ii) गणना में सरल (Easy of calculation)-विस्तार की गणना सबसे अधिक सरलता से की जा सकती है। चतुर्थक विचलन की गणना करने के लिए उच्च चतुर्थक (Q3) तथा न्यूनतम (Q3) की गणना करनी पड़ती है, परन्तु इनकी गणना सरलता से की जा सकती है। माध्य विचलन तथा प्रमाण विचलन की गणना के लिये थोड़ी अधिक विधिपूर्वक गणना करने की आवश्यकता होती है।
(iii) सरल व्याख्या (Simple interpretation)-परिक्षेपण के सभी मापों की सरलता से व्याख्या की जा सकती है और उन्हें सरलता से समझा जा सकता है। विस्तार तथा चतुर्थक विचलन सामान्य रूप से परिक्षेपण को मापते हैं। माध्य विचलन तथा प्रमाण विचलन परिक्षेपण का माप केन्द्रीय मूल्य के विचलन के रूप में करते हैं । अत: माध्य विचलन तथा प्रमाण विचलन मूल्य के परिक्षेपण के बारे में अधिक अच्छी जानकारी देते हैं।
(iv) सभी मूल्यों पर आधारित (Based on all values)- विस्तार तथा चतुर्थक विलचन, सभी मूल्य पर निर्भर नहीं करते । इसके विपरीत माध्य विचलन तथा प्रमाण विचलन चरों के सभी मूल्यों के लेते हैं। विस्तार तो चरम (Extrement) मूल्यों से बहुत ही प्रभावित होती हैं।
(v) बीजगणितीय व्यवहार (Algebrical treatment)- लगभग परिक्षेपण के सभी मापों से बीजगणितीय व्यवहार किया जा सकता है।
प्रश्न 20.(क) व्यक्तिगत श्रेणी तथा खण्डित श्रेणी से माध्य विचलन की गणना कैसे की जाती है?
(How is mean calculated in the individual service and discrete series.)
(ख) निम्नलिखित सारणी से माध्यिका तथा माध्य विचलन ज्ञात करें।
(Calculate mean deviation from median and mean.)
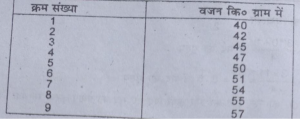
उत्तर-(क) व्यक्तिगत श्रेणी से माध्य विचलन की गणना (Calculation of mean Deviation from Individual Series)-0 वह माध्य ज्ञात करें जिससे विचलन ज्ञात करना है।
(ii) माध्यिका/माध्य से (+) या (-) संकेतों की अवहेलना करते हुए विचलन ज्ञात करें।
(iii) इन विचलनों का योग £D ज्ञात करें।
(iv) कुल योग (£D) को मदों की कुल संख्या से विभाजित करें। सूत्र के रूप में माध्य विचलन =£D/N
(v) भजनफल माध्य विचलन होगा।
(ख) खण्डित श्रेणी से माध्य विचलन की गणना (Calculation of Mean Deviation in Discrete series)-(i) दी हुई श्रेणी से माध्यिका ज्ञात करें।
(ii) के चिह्नों की अवहेलना करते हुए विलचन ज्ञात करना व £f|D| ज्ञात करें।
(iii) विचलनों को इनकी आवृत्तियों से गुणा करके इनका योग (£f|D|) ज्ञात करना।
(iv) अन्त में, प्राप्त योगफल को मदों की संख्या से भाग करना । इस प्रकार माध्य विचलन का मूल्य प्राप्त होगा।
मध्यिका से मांध्य विचलन की गणना

माध्य से माध्य विलयन की गणना (Calculation of Mean Deviation from Mean)
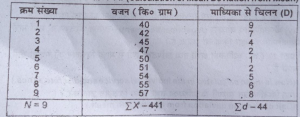
X=ΣΧ /N =441\9 =49 कि० ग्राम
पमान्तर विचलन Σd/N= 44/9=4.98 कि० ग्राम
प्रश्न 21.(क) अखाण्डित श्रेणी से माध्य की गणना कैसे की जाती है।
How is mean deviation calculated in case of continuous series?
(ख) नीचे 50 श्रमिकों की मजदूरी का वितरण दिया गया है। माध्य विचलन ज्ञात करें।
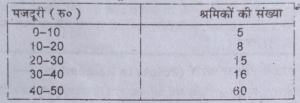
उत्तर-(क) अखण्डित श्रेणी के माध्य विचलन की गणना में निम्नलिखित चरण ‘नहित है
(i) वर्गान्तर के मध्य बिन्दु ज्ञात करा । मान लो वर्गान्तर 0-10, 10-20, 20-30 आदि हैं तो इनके मध्य बिन्दु 5,15, 25 होंगे।
(ii) मध्य बिन्दुओं से माध्यिका या माध्य ज्ञात करें।
(iii) + चिह्नों की अवहेलना करते हुए विचलन ज्ञात करना £D ज्ञात करना ।
(iv) विचलनों को उनकी आवृत्तियों (f) से गुणा करना फिर उनका योग निकालना ! योग को £fD से प्रकट करना।
(v) अन्त में प्राप्त योग को मदों की संख्या से भाग करना । इस प्रकार माध्य विचलन ज्ञात हो जायेगा।
(ख) माध्य विचलन किसी भी साध्य द्वारा निकाला जा सकता है, यहाँ माध्यों का प्रयोग करके माध्य-विचलन की गणना की गई है।
माध्य से माध्य विचलन ज्ञात करना

समान्तर माध्य (X)=Σfm /N =1350/50=27
माध्य से माध्य विचलन= Σfd/N =472/50
= 9.44
