Bihar Board 12th Physics Important Questions Long Answer Type Part 2 in Hindi

Bihar Board 12th Physics Important Questions Long Answer Type Part 2 in Hindi

BSEB 12th Physics Important Questions Long Answer Type Part 2 in Hindi

प्रश्न 1. विद्युत चुम्बकीय प्रेरण क्या है ? फैराडे के विद्युत प्रेरण का नियम लिखें तथा व्याख्या करें।
उत्तर: विद्युत चुम्बकीय प्रेरण (Electro magnetic induction)- विद्युत और चुम्बक ‘में गहरा सम्बन्ध है। इसे फैराडे (Faraday) ने अपने अनेक प्रयोगों के आधार पर दिखलाया है। इनके अनुसार चुम्बकीय क्षेत्र से विद्युत धारा उत्पन्न की जा सकती है।

A एक बन्द कुण्डली तथा NS एक चुम्बक है। कुण्डली में एक galv.G लगा है। चुम्बक को कुण्डली के नजदीक लाने तथा दूर ले जाने से कुण्डली में एक वि० वा० बल उत्पन्न होता है। इसके फलस्वरूप विद्युत धारा प्रवाहित होता है। यह धारा तब तक प्रवाहित होता रहता है तब तक कि कुण्डली तथा चुम्बक के बीच आपेक्षिक गति रहती है। इस धारा को प्रेरित धारा (Induce current) तथा वि० वा० बल को.”प्रेरित वि० वा० बल” (Inducee.m.f.) कहते हैं। इस घटना को विद्युत चुम्बकीय प्रेरण,(Electro magnetic induction) कहते हैं। इस घटना को विद्युत चुम्बकीय प्रेरण (Electro magnetic induction) कहते हैं।

फैराडे के विद्युत चुम्बकीय प्रेरण का नियम (Faraday’s law of electro magnetic induction) –
पहला नियम – जब किसी बन्द परिपथ में चुम्बकीय बल रेखाओं की संख्या में परिवर्तन होता है तो परिपथ में प्रेरित वि० वा० बल उत्पन्न होता है और यह तब तक रहता है जब तक परिवर्तन होता रहता है।

दूसरा नियम – किसी कुण्डली में उत्पन्न प्रेरित वि० वा० बल का परिमाण

1. कुंडली से होकर जाने वाली बल की संख्या के परिवर्तन के दर के समानुपाती
2. लपेटनों की संख्या के समानुपाती होता है।

व्याख्या – मान लिया कि किसी कुण्डली से जाने वाली चुम्बकीय बल रेखाओं की संख्या N₁ है। t समय के बाद यह संख्या N₂ हो जाती है।

Case I – यदि N₂ > N₁ हो तो N₂ – N₁ = धनात्मक
∴ t समय में बल रेखाओं की संख्या में परिवर्तन = N₂ – N₁

प्रश्न 2. प्रत्यावर्ती धारा (A.C.) क्या है? A.C. के औसत मान तथा मूल औसत वर्ग मान के लिए व्यंजन प्राप्त करें।
उत्तर:

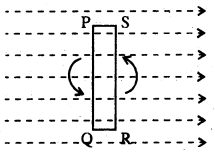
प्रत्यावर्ती धारा (Alternating current):-जब किसी कुण्डली को चुम्बकीय क्षेत्र में तेजी से घुमाया जाता है तब इसमें एक प्रेरित वि० वा० बल उत्पन्न होता है। कुण्डली के एक चक्र लगाने पर यह मान दो बार शून्य तथा दो बार अधिकतम होता है। इसका कारण यह होता है कि कुण्डली के आधे चक्कर में वक्र रेखाएं कुण्डली में PQ में प्रवेश करती है तथा RS से बाहर निकलती है। फिर शेष आधे चक्कर में कुण्डली की भुजा बदल जाती है और बल रेखाएं RS से प्रवेश कर PQ से बाहर निकल जाती है। इसके फलस्वरूप आधे चक्कर में प्रेरित वि० वा० बल एक दिशा में तथा दूसरे आधे चक्कर में विपरीत दिशा में होती है। दूसरा कारण इसपर पड़ने वाली बल रेखाओं की संख्या में परिवर्तन का अधिकतम होना होता है। इस स्थिति में कुण्डली में उत्पन्न धारा भी इसी तरह से बदलती रहती है। इस धारा की “प्रत्यावर्ती धारा (Alternating current)” या A.C. कहते हैं।

अत: “A.C. वह धारा है जो मान और दिशा में बदलता रहता है तथा कुण्डली के एक चक्कर में बदलने का भी एक चक्र (sin e curve) की तरह परिवर्तन होता है। इसीलिए इसे “ज्यावक्रीय धारा (Sinusoidal alternating current)” भी कहते हैं।
किसी t समय में उत्पन्न धारा (i) =i₀ sinwt
जहाँ i₀ → धारा का अधिकतम मान
w → कुण्डली का कोणीय वेग।

(i) प्रत्यावर्ती धारा का तात्कालिक मान तथा शिखर मान :(Instantaneous Value and Peak value of A.C.) –
A.C. का समीकरण i=i₀ sin wt
इस i की A.C. का तात्कालिक मान (Instantaneous value) तथा i₀ की धारा का “शिखर मान (Peak Value)” कहते हैं।

(ii) A.C. का औसत मान (Mean value of A.C.) –
कुण्डली के आधे आवर्तकाल में उत्पन्न प्रत्यावर्ती धारा के मान के औसत को “प्रत्यावर्ती धारा का औसत मान (Mean value of A.C.)” कहते हैं।
इसे “i_m” से सूचित करते हैं।

हम जानते हैं कि t समय में उत्पन्न प्रत्यावर्ती धारा (i) = i₀ sin wt
जहाँi₀ → धारा का अधिकतम मान
w → कुण्डली का कोणीय वेग


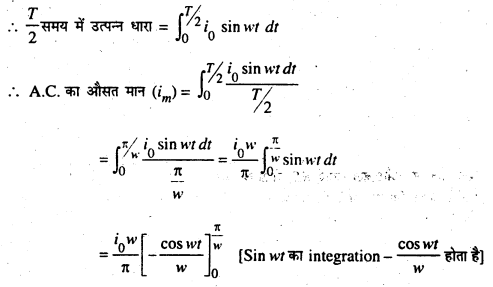
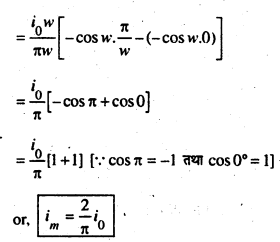
अर्थात im = 2/π धारा का अधिकतम मान

(iii) A.C. का मूल औसत वर्ग या आभासी मान (Root Mean square or virtual value of A.C.) –
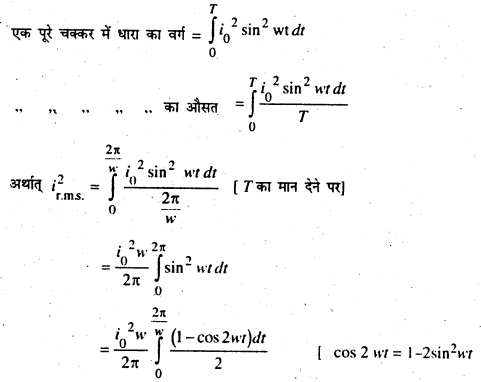
एक पूरे आवर्त काल पर उत्पन्न प्रत्यावर्ती धारा के वर्ग के औसत के वर्गमूल को धारा का “मूल औसत वर्ग मात्र” या आभासी मान (Root mean square value or virtual value) कहते हैं।

इसे i_r.m.s से सूचित करते हैं।
किसी t समय में उत्पन्न प्रत्यावर्ती धारा (i) = i₀ sin wt
∴ धारा का.वर्ग (i²) =i₀²-sin²wt

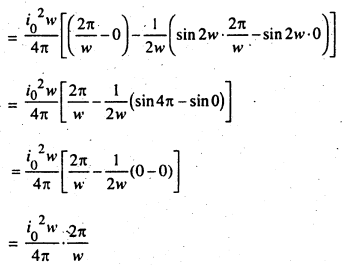
प्रश्न 3. एक छोटे चुम्बक या चुम्बकीय द्विध्रुव के कारण किसी स्थिति में – (i) चुम्बकीय विभव तथा (ii) चुम्बकीय क्षेत्र की तीव्रता का व्यंजक प्राप्त करें।
उत्तर:
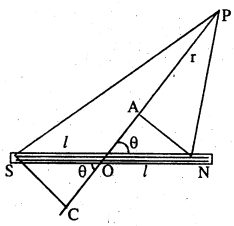
(i) चुम्बकीय विभव (Magnetic potential)-मानलिया कि NS एक छोटा चुम्बक या चुम्बकीय द्विध्रुव है। इसकी लम्बाई 2l तथा ध्रुव की शक्ति m है। इसका मध्य बिन्दु O है। O से r दूरी पर P एक विन्दु है। इस बिन्दु पर चुम्बकीय विभव निकालना है।
मानलिया कि ∠NOP = θ
N ध्रुव के कारण P पर विभव

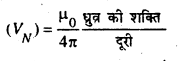
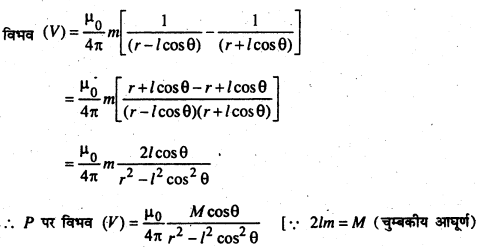
यदि चुम्बक छोटा हो तो l²cos²θ का मान बहुत कम होगा जिसे r² की तुलना में छोड़ा
जा सकता है।

एक छोटा चुम्बक या चुम्बकीय द्विध्रुव के कारण किसी बिन्दु पर चुम्बकीय प्रेरण (Magnetic induction at any point due to magnetic dipole or a small magnet]-

मानलिया कि NS एक छोटा चुम्बक या चुम्बकीय ध्रुव है। इसका चुम्बकीय आघूर्ण M है। मध्य बिन्दु O से r दूरी पर P एक बिन्दु है। P पर विभव की सहायता से चुम्बकीय प्रेरण निकालना है।
मानलिया कि ∠NOP = θ
NS के कारण P पर विभव

यहाँ पर V का मान r तथा θ के साथ बदलता है। दोनों के परिवर्तन से विभव का परिवर्तन देखना है।

(i) r को बदलने पर-
विभव तथा प्रेरण के बीच सम्बन्ध से,
चुम्बकीय प्रेरण (B_r) = −dv/dr

(ii) θ को परिवर्तन करने पर –

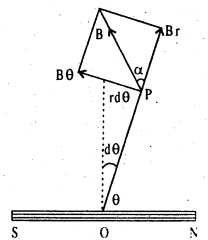
मानलिया कि θ कोण को dθ से बदलते हैं।
फिर θ = l/r सूत्र से
यहाँ पर dθ = l/r = या, l = rdθ
अब विभव तथा प्रेरण के सम्बन्ध से,
चुम्बकीय प्रेरण (B_θ) = −dV/rdθ

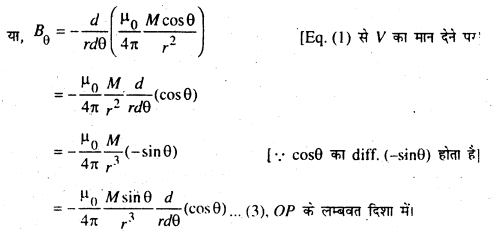
अब P बिन्दु पर B_r तथा B_θ दो चुम्बकीय प्रेरण कार्य करते हैं। इन दोनों से एक आयत की कल्पना करते हैं। इसका कर्ण, मान तथा दिशा में परिणामी चुम्बकीय प्रेरण (B) को दिखलाता है।
: P पर परिणामी चुम्बकीय प्रेरण, B² = B_r² + B_θ²

मानलिया कि परिणामी प्रेरण (3), B_r के साथ α कोण बनाता है।

प्रश्न 4.  स्थापित करें।
या, गोलीय पृष्ठ से अपवर्तन का सूत्र प्राप्त करें।
उत्तर:

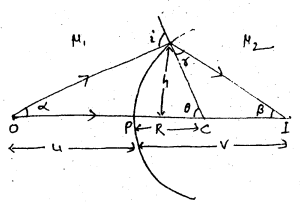
चित्र में गोलीय पृष्ठ दर्शाया गया है जो दो माध्यमों को अलग करता है जिसका अपवर्तनांक क्रमशः μ₁, एवं μ₂, है। इसके मुख्य अक्ष के बिन्दु O पर कोई बिम्ब रखा गया है जिससे निकलने वाली किरणें गोलीय पृष्ठ से अपवर्तन होने के बाद मुख्य अक्ष के बिन्दु I पर प्रतिबिम्ब का निर्माण करती है। माना कि,
आपतन कोण = i
अपवर्तन कोण = r
Snell के नियम से,

प्रश्न 5. पतले लेंस से अपवर्तन का सूत्र प्राप्त करें।
उत्तर:

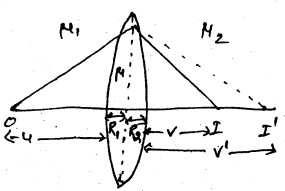
चित्र में एक पतला लेंस दर्शाया गया है जो दो माध्यमों को अलग करता है जिनका अपवर्तनांक μ₁, एवं μ₂ है। लेंस का अपवर्तनांक μ है। इसके मुख्य के बिन्दु O पर कोई बिम्ब रखा गया है जिससे निकलने वाली किरणें पहले पृष्ठ से अपवर्तित होने के बाद मुख्य अक्ष के बिन्दु ” पर प्रतिबिम्ब का निर्माण करती है जो लेंस के दूसरे पृष्ठ के लिए बिम्ब ५. का कार्य करता है जिसका अतिम प्रतिबिम्ब मुख्य अक्ष के बिन्दु I पर बनता है।
लेंस के पहले पृष्ठ से अपवर्तन के सूत्र स,

अतः पूरे लेंस के लिए

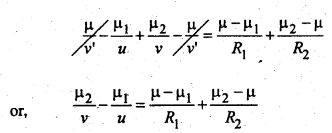
यदि लेंस के दोनों तरफ का माध्यम हवा हो तो,
μ₁ = μ₂ = 1

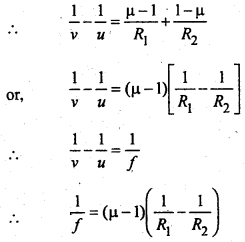
प्रश्न  6. कुछ दूरी पर रखे हुए दो लेंसों की समतुल्य फोकस लम्बाई निकालें।
उत्तर: मानलिया कि L₁ तथा L₂ दो पतले लेन्स (thin lens) हैं। दोनों का मुख्य अक्ष (Principal axis) एक ही सरल रेखा पर रहता है। इनके बीच की दूरी d है। इसकी फोकस लम्बाई क्रमशः f₁ तथा f₂ है।

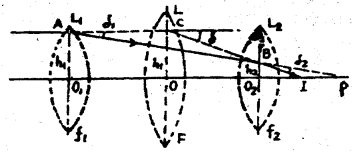
मान लिया कि वस्तु अनन्त पर है। इससे किरणें प्रधान अक्ष से समानान्तर चलकर L₁ लेंस के A बिन्दु पर आपतित होती हैं। प्रकाश केन्द्र से इसकी ऊंचाई h₁ है। लेन्स से वर्तित होकर किरणें P बिन्दु पर पहुंचती है।

∴  O₁P = प्रतिबिम्ब की दूरी = फोकस लम्बाई (f₁)
यह किरण L₂ लेन्स के B बिन्दु पर आपतित हो जाती है। प्रकाश केन्द्र से इसकी ऊंचाई h₂ है। इस लेन्स से वर्तित होकर किरणें I पर मिलती है। अतः अनन्त पर स्थिति वस्तु L₁ तथा L₂ लेन्स से प्रतिबिम्ब I बनता है।

अब L₁ तथा L₂ लेन्स के बदले एक ऐसा लेन्स L लेते हैं जिसके द्वारा अनन्त की वस्तु का प्रतिबिम्ब उसी स्थान I पर उसी आवर्द्धन (magnification) का बनें। L लेन्स को L₁ तथा
L₂ का समतुल्य लेन्स (Equivalent lens) कहते हैं।
अतः OI = L से प्रतिबिम्ब की दूरी = फोकस लम्बाई (F)
मान लिया कि L₁L₂ तथा L लेन्स से किरण का विचलन क्रमश δ₁, δ₂, तथा δ है।

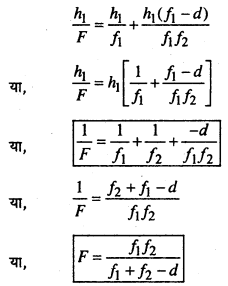
दोनों लेन्सों से समतुल्य लेन्स (Equivalent lens) की दूरी –
मानलिया कि L₂ लेन्स L की दूरी = x
अब ΔCOI और ΔBO₂I सदृश्य (similar) हैं।
अतः उनकी भुजाएँ समानुपाती होगी।

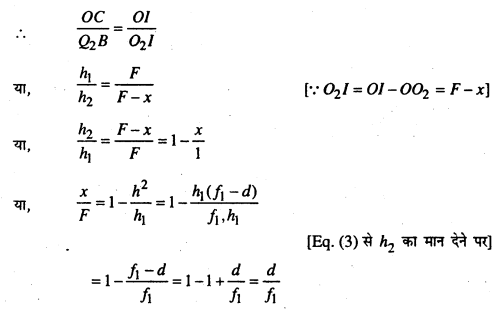
प्रश्न 7. प्रकाश के तरंग सिद्धांत के आधार पर प्रकाश के परावर्त्तन या अपवर्तन के नियमों की व्याख्या करें।
उत्तर:

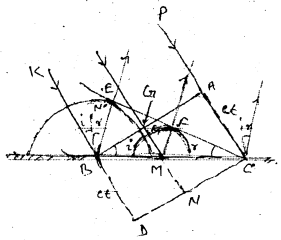
प्रकाश के परावर्तन के नियम की व्याख्याः मान लिया BC एक समतल परावर्तक सतह पर एक समतल तरंगाग्र AB आपतन कोण i बनाते हुए आपतित होता है। चित्र में ये दोनों कागज तल के अभिलम्ब दिखलाये गये  हैं। PA तथा KB आपतित किरण हैं जो आपतित तरंगाग्र पर लम्ब है। AC = BD = Ct खींचा गया जहाँ c प्रकाश की चाल तथा A से द्वितीयक तरंगाग्र को C तक आने में लगा समय है। अतः DC, t समय बाद परावर्तक सहत की अनुपस्थिति में तरंगाग्र का नया रूप होता . है। लेकिन परावर्तक सतह की उपस्थिति में B से उत्पन्न द्वितीयक तरंगिका t समय में BE=ct = BD दूरी तय करता है। BE को त्रिज्या एवं B को केन्द्र मानकर काल्पनिक गोला खींचा गया तथा इस पर c से स्पर्श तल CE खींचा गया। अब अगर यह दिखलाया जाय कि आपतित्त तरंगाग्र के किसी बिन्दु G से उत्पन्न द्वितीयक तर्रागका t समय में परवर्तक सतह के M बिन्दु तक तथा फिर परावर्तित होकर तल CE को ठीक स्पर्श करता है तो CE अवश्य ही । समय बाद परावर्तित तरंगाग्र होगा। M से तल CE पर लम्ब MF खींचा गया।

अतः M से चली द्वितीयक तरंगिका परावर्तक सतह भी उपस्थिति में ठीक CE तक के बिन्दु F तक पहुँच जायेगी। अतः t से समय बाद CE परावर्तित तरंगाग्र होगा। तथा ∠ECB =r परावर्तन कोण अब चित्र की ज्यामिति से,

यह परावर्तन का दूसरा नियम है।
चित्र की ज्यामिति से यह भी स्पष्ट है कि आपतित किरण KB तथा परावर्तित किरण BE उसी तल में है जिस तल आपतन बिन्दु B पर खींचा गया अभिलम्ब BN’ है। यह परावर्तन का दूसरा नियम है।

अथवा, अपवर्तन के नियम की व्याख्या :
मानलिया कि XY सतह दो सामाग्री पारदर्शी माध्यमों को अलग करने वाला समतल सतह है इन माध्यमों में प्रकाश की चाल क्रमशः C₁ तथा C₂ है। आयततन कोण i बनाते हुए एक समतल तरंगाग्र AC तरंगाग्र कागज तल के अभिलम्ब है। A बिन्दु से उत्पन्न द्वितीयक तरंगिका में दूसरे माध्यम में चलकर AP=C₂t तय करती है जहाँ t = पहले माध्यम में आपतित तरंगाग्र AC के C बिन्दु से उत्पन्न द्वितीयक तरंगिका को अपवर्तक सतह के B बिन्दु तक पहुंचने का समय है। स्पष्टतः दूसरे माध्यम की अनुपस्थिति में A से उत्पन्न द्वितीयक तरंगिका AM=C₁t=CB दूरी तय करती ओर BH द्वितीयक तरंगाग्र होता।

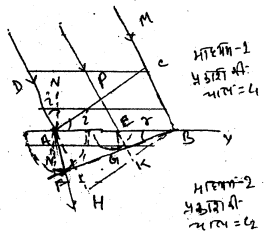
AF = C₂t त्रिज्या का A बिन्दु को केन्द्र मान कर काल्पनिक गोला खींचा गया तथा B से ‘गोला पर स्पर्श तल BF खींचा गया। BFt समय बाद अपवर्तित तरंगाग्र होगा यदि यह दिखला दिया जाय की आपतित तरंगाग्र में किसी बिन्दु P से उत्पन्न द्वितीयक तरंगाग्र t समय में अपवर्तक सतह के बिन्दु E तक तथा फिर सतह BF तक ठीक ठीक पहुंचता है। E से EG लम्ब तक BF पर खींचा गया।.
समरूप ΔABF और BGE से,

अर्थात् पहले माध्यम में तरंगाग्र को EK दूरी तय करने लगा समय = दूसरे माध्यम में । तरंगिका को EG दूरी करने में लगा समय अतः P बिन्दु से चली तगिका t समय में समतल BF को G बिन्दु पर ठीक-ठीक स्पर्श करती है। अतः, t समय बाद BF अपवर्तित तरंगाग्र होगा।

जहाँ 1_μ2 पहले माध्यम की अपेक्षा दूसरे माध्यम का अपवर्तनाक है। अतः आपतन कोण का sine (ज्या) तथा अपवर्तन कोण का sine का अनुपात नियत है यदि अपवर्तन का दूसरा नियम (स्नेल का नियम) है।

चित्र की ज्यामिति से स्पष्ट है कि आपतित किरण, अपवर्तित किरण एवं आपतन विन्दु पर खींचा गया अभिलम्ब तीनों एक ही तल में है।
यह अपवर्तन का प्रथम नियम है।

प्रश्न 8. स्वच्छ चित्र खींचकर यौगिक सूक्ष्मदर्शी की बनावट तथा क्रिया का वर्णन करें। इसके आवर्द्धन क्षमता के लिए व्यंजक प्राप्त करें।
उत्तर: यौगिक सूक्ष्मदी Compound Microscope)-यौगिक सूक्ष्मदर्शी (Compound microscope) वह यंत्र है जिसके द्वारा छोटी वस्तुओं को बड़ा रूप में देखा जा सकता है।

बनावट तथा क्रिया -इसमें L₁ तथा L₂ दो उत्तल लेन्स (Convex Lens) हैं। L₁ की फोकस लम्बाई तथा आकार छोटा परन्तु L₂ को फोकस लम्बाई तथा आकार बड़ा होता है। L₁ ताल वस्तु के नजदीक रहता है। इसलिए इसे वस्तु ताल (Object lens or objective) कहते हैं। L ₂ताल आँख के निकट रहता है। इसीलिए इसे नेत्र ताल (Eye lens or Eye pieces) कहते हैं। दोनों लेन्स नली के अन्दर एक ही अक्ष पर टिका रहता है। इसमें नेत्र ताल बाकी नली को रैक और पिनियम व्यवस्था (Reack and PiniumArrangement) से आगे-पीछे खिसकाया जा सकता है। L₁ तथा L₂ लेन्स के बीच की दूरी को सूक्ष्मदर्शी की लम्बाई कहते हैं।

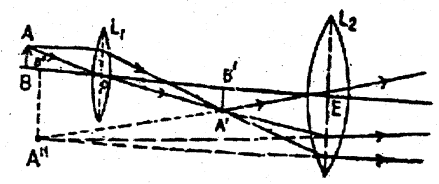
मान लिया कि AB एक छोटी वस्तु है जिसे सूक्ष्मदर्शी से देखना है। इसे वस्तु लेन्स की फोकस लम्बाई से थोड़ा अधिक दूरी पर रखते हैं।L, लेन्स से इसका वास्तविक, उल्टा तथा बड़ा प्रतिबिम्ब A’B’ पर बनता है।

फिर A’B’ नेत्र लेन्स के लिए वस्तु का काम करता है। इससे इसका प्रतिबिम्ब A”B” ‘ बनता है। नेत्र लेन्स को इतना आगे-पीछे करते हैं कि A”B” स्पष्ट दिखाई पड़े। इस समय नेत्र लेन्स से A’B’ की दूरी स्पष्ट दृष्टि की न्यूनतम दूरी (D) के बराबर होती है। यह प्रतिबिम्ब काल्पनिक, सीधा तथा बड़ा होता है।
आवर्धन क्षमता(Magnifying Power)-

फिर नेत्र लेन्स के लिए-
इसमें वस्तु की दूरी (u) तथा प्रतिबिम्ब की दूरी (ν) negative होता है।
लेन्स के सूत्र से,

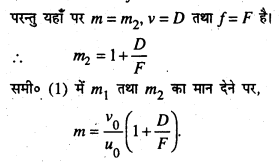
प्रश्न 9. Fresnel biprism द्वारा प्रकाश के तरंग की लम्बाई के मापने की विधि का सिद्धान्त वर्णन करें।
या, Fringe के चौड़ाई का व्यंजक प्राप्त करें।
उत्तर: फ्रेशेनल द्विकप्रिज्म – मान लिया कि ABC एक द्विकप्रिज्म (Biprism) है। इसका वर्तक कोण लगभग 179° होता है। यह दो प्रिज्मों के मिलने से बनता है। दोनों का आधार एक साथ जुड़ा रहता है।
S एक छिद्र (Slit) है, इसे एकवर्णी (Monochromatic) प्रकाश से प्रकाशित किया जाता है।

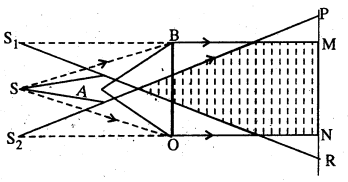
S को प्रिज्म के वर्तक कोण (Refracting edge) के समानान्तर रखा जाता है। S से निकलने वाली किरणें प्रिज्म के AB तथा AC सतह पर आपतित होती हैं। वर्तित होने के बाद S का S₁ तथा S₂ दो काल्पनिक प्रतिबिम्ब बनते हैं। यह S₁ तथा S₂ दो कलाबद्ध स्रोत (Coherent source) की तरह काम करते हैं। Biprism से थोड़ी दूरी पर PQ एक पर्दा है। इस पर्दा के MN भाग के बीच में व्यतिकरण धारियों (Interference fringes) दिखलाई पड़ते हैं। इसमें बहुत सी चमकीली तथा अन्धेरी रेखाएं होती हैं।

सिद्धांत (theory)-पर्दा पर O एक बिन्दु की कल्पना करते हैं। यह S₁ तथा S₂ से बराबर दूरी पर है। O पर तरंगें S₁ और S₂ से एक ही कला में पहुँचती हैं। अतः O पर चमकीली धारा दिखलाई पड़ती है।

O से x दूरी पर एक बिन्दु P की कल्पना करते हैं। P से S₁ तथा S₂ को मिलाया।

यदि P पर S₁ तथा S₂ से तरंगें एक ही कला में पहुंचती हैं तब चमकीली धारी बनती है।
इस समय S₂P – S₁P = nλ … (1)
जहाँ n = 0, 1, 2, 3…..
λ = प्रकाश की तरंग लम्बाई
परन्तु यदि P पर S₁ तथा S₂ से तरंगें विपरीत कला में मिलती हैं तब काली धारियाँ (Dark fringes) उत्पन्न होती हैं।
इस समय S₂P – S₁P = (2n+1)λ/2 …(2)
अब मान लिया कि S₁ S₂ = d

SS₁= SS₂ = d/2
Source से पर्दा की दूरी = D
S₁ से S₁M तथा S₂ से S₂N, OP पर लम्ब खींचा।
ΔS₁MP में S₁P = S₁M² + MP²
D² + (x−d/2)² [MP = OP -OM – x – d/2]



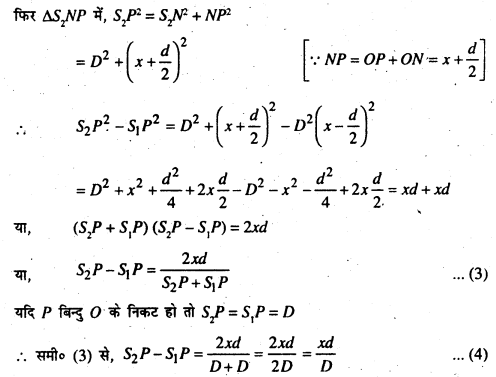
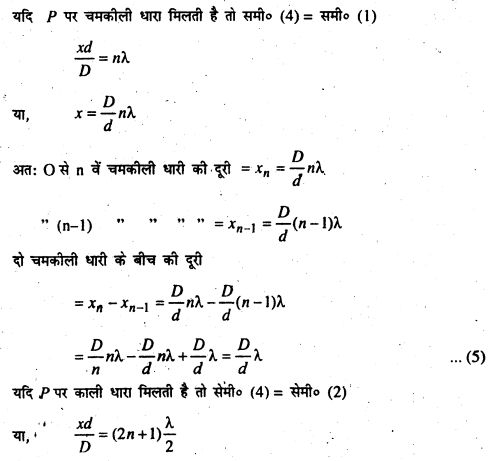
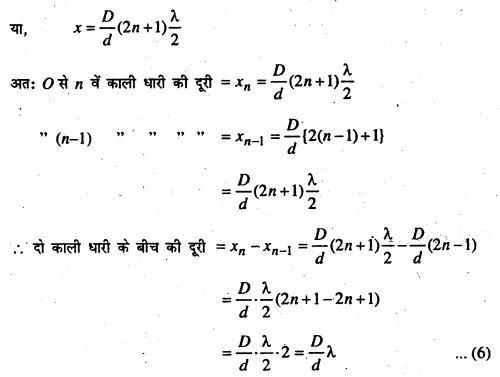
समी० (5) और (6) से हम पाते हैं कि दो चमकीली तथा दो काली धारियों के बीच की दूरी समान है। अतः चमकीली तथा काली धारियों की चौड़ाई भी समान होगी।

समी० (7) की सहायता से Fringe की चौड़ाई एवं समी० (8) की सहायता से तरंग लम्बाई ज्ञात की. जा सकती है।

प्रश्न 10. L-C-R परिपथ में प्रवाहित धारा के लिए व्यंजक प्राप्त करें। इस परिपथ की शक्ति के लिए भी व्यंजक प्राप्त करें।
उत्तर:

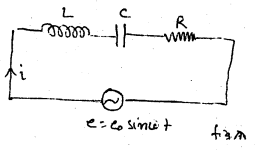
L-C-R परिमेय : चित्र
(1) में प्रेरकत्व (L), संधारित्र (c) एवं प्रतिरोध (R) को A.C. स्रोत e = e_o sin ωt के स्थान श्रेणी क्रम में दिखलाया गया है। इस परिपथ का प्रति बाधा z ज्ञात करने के लिए चित्र। (2) में सदिश आरेख दिखलाया गया है। इस आरेख से स्पष्ट है कि परिपथ की प्रतिवाधा

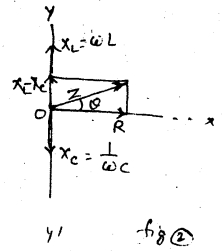
जहाँ x_L = ωL = प्रेरकत्वीय प्रतिघात है।
अतः इस परिपथ की धारा i=
i₀ sin (ωt + Φ ) =