Bihar Board 12th Physics Important Questions Long Answer Type Part 1 in Hindi

Bihar Board 12th Physics Important Questions Long Answer Type Part 1 in Hindi

BSEB 12th Physics Important Questions Long Answer Type Part 1 in Hindi

प्रश्न 1. Gauss के प्रमेय को लिखें तथा स्थापित करें? आविष्ट समतल चालक के समीप स्थित बिन्दु पर तिव्रता की गणना करें।
उत्तर: गॉस के अनुसार-“किसी बंद क्षेत्र का विद्युतीय फ्लक्स उस क्षेत्र के आवेश का 1/ϵ₀ के गुणनफल के बराबर होता है।
अर्थात् Φ = 1/ϵ₀

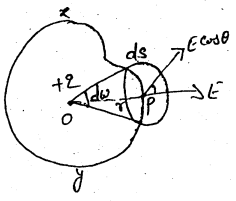
प्रमाण:-
चित्र में एक बंद क्षेत्र xy दर्शाया गया है। इसके अंदर स्थित बिन्दु O और r दूरी पर सतह पर कोई बिन्दु P लिया गया है। बिन्दु P को घेरते हुए एक छोटे बंद क्षेत्र की कल्पना की जाती है जिसका क्षेत्रफल ds है।
यदि बिन्दु P पर विद्युत तीव्रता E हो

Φ = Eds cosθ

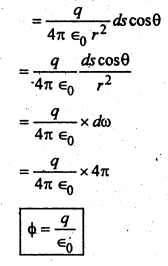
आविष्ट समतल चालक के कारण तीव्रता-

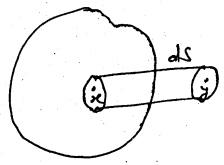
चित्र में एक आविष्ट समतल चालक दर्शाया गया है जिसका पृष्ठ घनत्व σ है। चालक के सतह के समीप अन्दर एवं x एवं y से गुजरने वाला बेलन का क्षेत्रफल ds है। चूंकि बिन्दु x आविष्ट सतह के अंदर स्थित हैं इसीलिए इस पर तीव्रता का मान शून्य होगा। यदि बिन्दु y पर तीव्रता E हो तो
Φ = Eds …(i)
गॉस के प्रमेय से,

प्रश्न 2. किसी चालक के स्थितिज ऊर्जा से क्या समझते हैं। आवेश वितरण में ऊर्जा हास का व्यंजक प्राप्त करें।
उत्तर: किसी अनाविष्ट चालक को आविष्ट करने में सम्पादित कार्य को चालक की ऊर्जा (स्थितिज ऊर्जा) कहा जाता है।
माना कि किसी चालक को q आवेश देने से उसका विभव शून्य से बढ़कर ν हो जाता है।

समी० (i), (ii) एवं (iii) स्थितिज ऊर्जा के व्यंजक है।
आवेश वितरण में ऊर्जा ह्रास का व्यंजक-
माना कि दो चालकों की धारिताएँ c₁ एवं c₂ तथा इनका विभव क्रमशः ν₁ एवं ν₂ है। अतः चालकों की कुल ऊर्जा

यदि चालकों के बीच आवेश वितरण के फलस्वरूप इनका उभयनिष्ठ विभव ν हो तो, आवेश वितरण के पश्चात्य कुल ऊर्जा

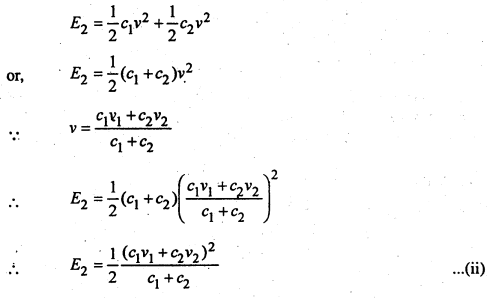
अतः ऊर्जा में हास
ΔE = E₁ – E₂

प्रश्न 3. वॉन डी-ग्राफ जनरेटर क्या है? वॉन डी-ग्राफ जनरेटर की बनावट एवं क्रिया। का वर्णन करें।
उत्तर: Van De Grar Ganerator (वॉन डी-ग्राफ जनरेटर):
यह निम्न स्रोत से बहुत उच्च विभव प्राप्त करने की एक विद्युत स्थैतिक मशीन है। इससे 10000V के स्रोत से कई मिलिय वोल्ट का विभव प्राप्त किया जा सकता है जिसका उपयोग electrons, protons तथा ions जैसे आवेशित कणों को त्वरित करने में किया जाता है।

यह निम्नलिखित दो सिद्धान्तों पर कार्य करता है
(i) तीक्ष्ण नोक की क्रिया पर तथा
(ii) आवेशित खोखला गोला के वाह्य पृष्ठ पर आवेश एक समान रूप से फैल जाता है।

बनावट :
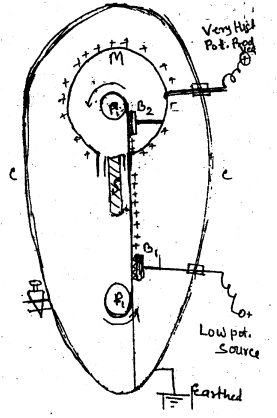
वॉन डी ग्राफ जनरेटर के मुख्य भाग को चित्र में दिखलाया गया है। इसमें मुख्य रूप से एक विशाल खोखला धातु का गोला पृथ्वी सतह से कुछ ऊंचाई पर विसंमवहित रूप स्तम्भ s पर रखा होता है। जिसके केन्द्र पर एक घिर्णी P₁ तथा इसके जैसा ही दूसरी घिर्णी P₂ गोले से बाहर पृथ्वी सतह के नजदीक लगा होता है। इन घिणीयों से होकर एक पतला अचालक पदार्थका फितागुजरता है जिसे मोटर द्वारा घुमाया जाता है। B₁ तथा B₂ धातु की नुकिली कंघीयों (comb) फीते के पास लगी होती है। पुली P₁ के पास वाली कंघी B₁ को स्प्रे कॉम्ब B₂ को संग्राहक कंघी कहा जाता है। B₂ धातु छड़ द्वारा गोला M से जुड़ा रहता है। ये सम्पूर्ण व्यवस्था धातु एक प्रकोष्ठ CC के भीतर होता है। गोला M एक धातु छड़ R से जुड़ा रहता है। जिसका दूसरा सीरा प्रकोष्ठ से बाहर है इस छड़ R पर उच्च विभव प्राप्त होता है।

(Working) :
जब स्प्रे कॉम्ब को पृथ्वी के सापेक्ष धनात्मक विभव (≅10⁴V) पर H.T. Source से किया जाता है।, तो नोक के स्वतः विसर्जन को क्रिया के कारण +ve आवेश का पवन (wind) फीता पर उत्पन्न होता है। यह बेल्टर पर घुम के गोले के भीतर ब्रश B₂ के पास पहुंचता है जहाँ नोक पर प्रेरण के कारण -ve आवेश बीकर वाले सिरे पर तथा दूसरे सिरे पर +ve उत्पन्न होते हैं। यह प्रेरित +ve आवेश तुरन्त गोले M के वाह्य पृष्ठ पर स्थनान्तरित हो जाता है।नोक के स्वतः विसर्जन क्रिया के कारण B₂ पर -ve आवेश का पवन (wind) स्थापित होता है जो बेल्ट के +ve आवेश को उदासीन कर देता है यह क्रिया लगातार होते रहती है और गोला M पर आवेश (+ve) बढ़ता जाता है।

गोलीय चालक की धारिता C = 4π∈R होता है।
एवं विभव V = Q/C = Q/4πϵ₀R जहाँ R गोले की त्रिज्याएँ जो नियत है। अत: V α Q.
अतः गोले M का विभव लगातार बढ़ता जाता है।
हवा का भंजन विभव (Break down field) लगभग 3 × 10⁶ V/m होता है अगर गोला का विभव किसी समय इस मान से बढ़ जाता है तो हवा आवेशित होने लगता है आवेश का लिकेज (Leakage) प्रारम्भ हो जाती है। इस लिकेज को कम करने के लिए जनरेटर को स्टील के प्रकोष्ट के भीतर रखकर इसमें उच्च दाब पर N₂ या मिथेन गैस को भर दी जाती है साथ ही प्रकोष्ठ को भूधृत कर दिया जाता है।

प्रश्न 4. संधारित्र क्या है? योगिक परावैद्युत वाले समान्तर प्लेट संधारित की धारिता के लिए व्यंजक प्राप्त करें। .
उत्तर: संधारित : चालकों की एक ऐसी व्यवस्था जिसमें किसी चालक की धारिता विना बढ़ाये कृत्रिम रूप से बढ़ायी जाती है, संधारित्र कहलाता है।
जब समान्तर प्लेट संधारित्र के प्लेटों के बीच एक से अधिक परावैद्युत माध्यम रखा जाता है तो इसे यौगिक संधारित्र कहा जाता है।

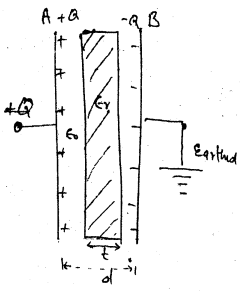
धारिता : मानलिया समान्तर प्लेट संधारित AB के प्लेटों के बीच स्थित हवा में t मुटाई का जिसका आपेक्षिक परावैद्युत ∈r है रखा गया है।
यदि संग्राहक प्लेट A पर +Q आवेश दिया गया है जिससे इसका पृष्ट
घनत्व σ = Q/A
प्लेटों के बीच हवा में तीव्रता E₁ = σ/ϵ₀
तथा परावैद्युत माध्यम में तीव्रता E₂ = σl/ϵ₀ϵ_r
अतः प्लेटों A तथा B के बीच विभवान्तर
V= एकांक (+1) को प्लेट B से A तक लाने में सम्पादित कार्य W/q
जहाँ W = हवा में लाने में कार्य (w₁) + परावैद्युत माध्यम में कार्य (w₂)
= F (d – t) + F (t)

प्रश्न 5. Biot-Savart नियम को लिखें। इस नियम की हायता से
(i) वृत्ताकार धारावाही तार के अक्ष पर
(ii) सरल रेखीय धारावाही तार के कारण कि बिन्दु पर
(iii) वृत्ताकार धारावाही तार के अश के किसी बिन्दु पर चुम्बकीय प्रेरण ( कोय बल क्षेत्र) की गणना करें।
उत्तर: Biot, Savart एवं.Laplace नामक वैज्ञानिकों ने धारावाही चालक के कारण उत्पन्न चुम्बकीय क्षेत्र के लिए एक गणितीय व्यंजक का प्रतिपादन किया जिसे Biot-Savart-Laplace का नियम कहा जाता है।

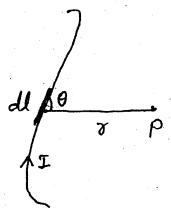
Biot-Savart नियम के अनुसार धारावाही चालक के अल्पांश dl द्वारा उत्पन्न चुम्बकीय क्षेत्र में किसी बिन्दु P पर उत्पन्न क्षेत्र का मान dB निम्न बातों पर निर्भर करता है-
(i) यह चालक से प्रवाहित धारा I का समानुपाती होता है।
अर्थात् dB ∝ I

(ii) यह चालक के अल्पांश dl का समानुपाती होता है।
अर्थात् dB ∝ dl

(iii) यह अल्पांश की लम्बाई तथा अल्पांश को बिन्दु P से मिलाने वाली रेखा के बीच के कोण का ज्या का समानुपाती होता है।
अर्थात् dB ∝ sinθ

(iv) यह अल्पांश से बिन्दु P से दूरी r के वर्ग का व्युत्क्रमानुपाती होता है।
अर्थात् dB ∝ 1/r²

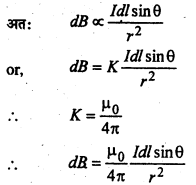
वृत्ताकार धारावाही तार के केन्द्र पर चुम्बकीय क्षेत्र की गणना-
चित्र में एक वृत्ताकार धारावाही तार दर्शाया गया है जिसकी त्रिज्या r एवं इससे प्रवाहित धारा I है।
तार.के अल्पांश dl के कारण उत्पन्न चुम्बकीय क्षेत्र


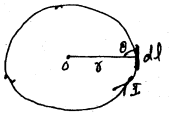
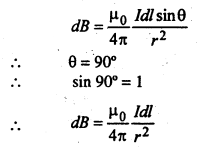
पूरे तार के कारण चुम्बकीय क्षेत्र

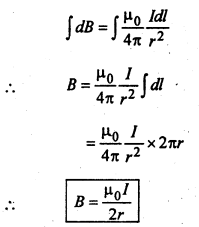
यदि तार में लपेटनों की संख्या N हो तो

सरल रेखीय धारावाही तार के कारण चुम्बकीय क्षेत्र की गणना-चित्र में एक सरल रेखीय धारावाही तार दर्शाया गया है जिससे प्रवाहित धारा I है। चालक से R दूरी पर कोई बिन्दु लिया गया है। तार के अल्पांश dx के कारण बिन्दु P पर चुम्बकीय क्षेत्र

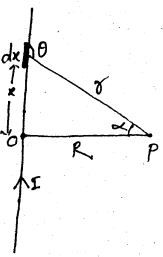
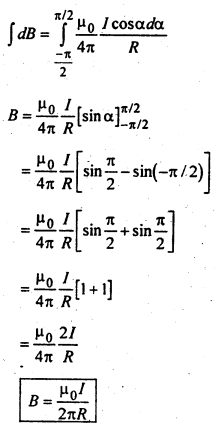
Case II :यदि तार की लम्बाई परिमित (सीमित) हो- इस स्थिति में समी० (ii) का समाकलन -α₁ एवं + α₂ के बीच करने पर.


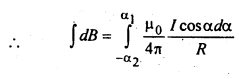
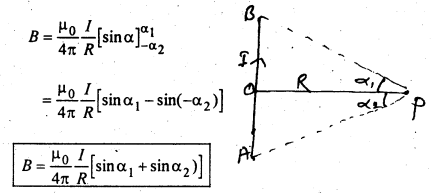
वृत्ताकार धारावाही तार के अक्ष के किसी बिन्दु पर चुम्बकीय क्षेत्र की गणना
चित्र में एक वृत्ताकार धारावाही तार दर्शाया गया है जिसका केन्द्र 0 त्रिज्या a एवं इससे प्रवाहित धारा ] है। इसके केन्द्र से r दूरी पर अक्ष पर कोई बिन्दु P लिया गया है जिस पर चुम्बकीय क्षेत्र की गणना करनी है।

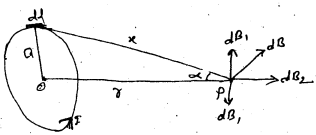
Biot-Savar Law के अनुसार बिन्दु P पर चुम्बकीय क्षेत्र

dB को दो परस्पर लम्बवत दिशाओं में विघटित करने पर इसका विघटित अवयव dB₁ एवं dB₂ है।
चूँकि dB₁ का परिणामी शून्य होगा अतः
बिन्दु P पर चुम्बकीय बल क्षेत्र
dB₂ = dB cosα

अतः पूरे तार के कारण चुम्बकीय क्षेत्र


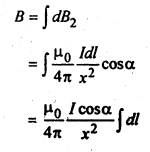
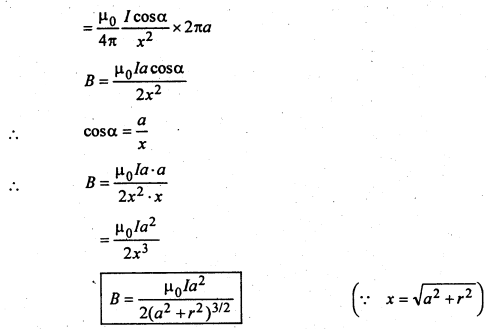
यदि वृत्ताकार धारावाही तार में लपेटनों की संख्या N हो तो

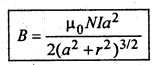
प्रश्न 6. प्रत्यावर्ती धारा डायनेमों या जनित्र का सिद्धांत सहित बनावट का वर्णन करें।
उत्तर: यह एक प्रकार का यंत्र होता है जिसके सहायता से यांत्रिक ऊर्जा को विद्युत ऊर्जा में परिवर्तित किया जाता है। इस यंत्र की क्रिया विद्युत चुम्बकीय प्रेरण के सिद्धांत पर आधारित है।

सिद्धांत : जब किसी कुंडली को चुम्बकीय क्षेत्र में घुमाया जाता है तो कुंडली से सम्बद्ध चुम्बकीय फ्लक्स में परिवर्तन होता है जिससे कुंडली में विद्युत बाहक बल प्रेरित हो जाता है तथा परिपथ में प्रत्यावर्ती धारा प्रवाहित होने लगती है।
बनावट :

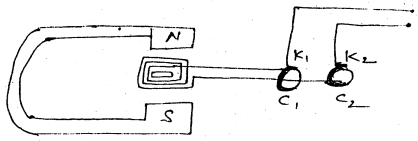
चित्र में प्रत्यवर्ती धारा डायनेमों या जनित्र दर्शाया गया है। इसके बनावट को निम्न भागों में बाँटा जाता है।

(i) आर्मेचर-यह ताँबे के तार की एक कुंडली होती है जो नरम लोहे के क्रोड पर लपेटी होती है। कुंडली में फेरों की संख्या बहुत अधिक होती है ताकि जब इसे शक्तिशाली चुम्बक के ध्रुवों के बीच तेजी से घूर्णित किया जाए तो उत्पन्न विद्युतं वाहक बल का शिखर मान ऊंचा हो। जाए।

(ii) क्षेत्र चम्बक यह एक शक्तिशाली विद्युत चुम्बक होता है जिसे दिष्ट धारा द्वारा सक्रिय किया जाता है। यह नाल चुम्बकों जैसा होता है जिसमें दोनों ध्रुवों के बीच कुंडली को रखकर घूर्णित किया जाता है।

(iii) सी वलय एवं ब्रश कुंडली के सिरे अलग-अलग विद्युत रोधित धातु के एक एक वलय c₁ एवं c₂ से जुड़े रहते हैं। आर्मेचर के घूर्णित होने पर ये वलय भी घूर्णित होते हैं। सी वलयc₁ एवं c₂ के सम्पर्क में कार्बन ब्रुश k₁ एवं k₂ लगे होते हैं। इन ब्रुशों का सम्बंध दो पेचों से जुड़ा होता है जिसके सहायता से विद्युतीय परिपथ में धारा प्रवाहित की जाती है।

प्रश्न 7. तने तारों वाला विभवमापी का वर्णन करें। इसके द्वारा सेलों के वि० वा० बल की तुलना तथा किसी सेल का वि० वा० बल निकालें।
उत्तर: तने तारों वाली विभवमापी(Stretched wire potentiometer)-इसके यंत्र में लकड़ी का एक आयताकार तख्ता रहता है। इसपर मैगनिन या कान्स्पटेन्टन का तार बिछा रहता है। सभी तार का अनुप्रस्थ क्षेत्रफल समान रहता है। तार को प्राय: 1 — 1 मीटर के पास दस टुकड़ों

में विभाजित कर देते हैं। एक टुकड़े का अन्तिम भाग, दूसरे के प्रारम्भिक भाग से तथा दूसरे का अन्तिम भाग तीसरे के प्रारम्भिक भाग से इत्यादि। ताम्बे की मोटी पत्ती द्वारा जुड़ा रहता है। पतले तार के शुरू छोर तथा अन्तिम तार के अन्त छोर को एक-एक संयोजक पेंच A तथा B से जोड़ देते हैं। तख्ता. पर तार के समानान्तर एक मीटर स्केल 5 से जुड़ा रहता है। तार के ऊपर एक जौकी J रहता है। जौकी प्रायः त्रिकोण रहता है। इसका निचला छोर झुरधार (Knifeedge) जैसा रहता है। इसे तार के समानान्तर खिसकाया जा सकता है। जौकी को नीचे दबाने पर यह तार को स्पर्श करता है। इस स्पर्श बिन्दु का पठन जौकी के चिह्न द्वारा स्केल पर नोट करते हैं।

उपयोग-

1. दो सेलों के वि० वा० बलों की तुलना करना।
2. किसी सेल का वि० वा० बल मापना।
3. किसी सेल का आन्तरिक प्रतिरोध ज्ञात करना।
4. किसी सेल की धारा का मान ज्ञात करना।
5. कम मान वाले प्रतिरोधों की तुलना करना।
6. दो प्रतिरोधों की तुलना करना।

(1) दो सेलों के वि० वा० बलों की तुलना (Comparison ofe.m.f. of two cells) – AB एक तने तारों वाला विभवमापी है। A और B के बीच एक सेल E, कुंजी Kतथा धारा नियंत्रक (Rheostate) RL श्रेणीक्रम में जुड़ा रहता है। M और N दो सेल हैं जिसके वि० वा० बल की तुलना करना है।

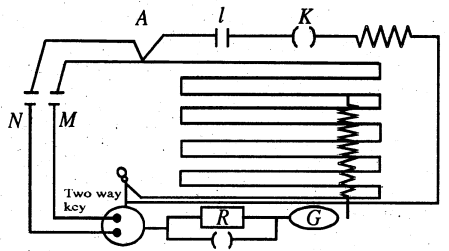
M और N के धन ध्रुव को A से तथा ऋण ध्रुव को Two way key से जोड़ देते हैं फिर तीसरे पेंच को प्रतिरोध बक्स R तथा Galv.G से जोड़ देते हैं। फिर इसका संबंध जौकी J से रहता है।

प्रयोग-प्रारम्भ में M सेल को परिपथ में रखते हैं। विभवमापी से धारा प्रवाहित होता है। इससे galv. में विक्षेप होता है। जौकी को खिसकाकर ऐसा स्थान खोजते हैं जिससे कि galv. में विक्षेप शून्य हो जाय। इसे संतुलन बिन्दु (Balance Point) कहते हैं। इस समय A से तार की लम्बाई (l₁) नोट कर लेते हैं।

मानलिया कि तार के इकाई लम्बाई का प्रतिरोध = r
∴ l₁ की लम्बाई का तार का प्रतिरोध = I₁r
सेल का वि० वा० बल = e₁
ओम के नियम से, वि० वा० बल = धारा प्रतिरोध
e₁ = cl₁r ….(1)
अब N सेल को परिपथ में रखते हैं। ऊपर की ही तरह जौकी से तार पर एक ऐसा बिन्दु खोजते हैं जिसके लिए galv. का विक्षेप शून्य हो जाय। इस समय A से तार की लम्बाई l₂ नोट कर लेते हैं।
l₂, लम्बाई के तार का प्रतिरोध = l₂r
N सेल का वि० वा० बल =e₂
प्रवाहित धारा =C
∴ e₂ = cl₂r      (2)
समी० (1) ÷ समी० (2),


समी० (4) में e₂ का मान पहले से मालूम रहता है तथा l₁ और l₂ का मान प्रयोग से निकाल लेते हैं। इससे e₁ ज्ञात हो जाता है।

प्रश्न 8. अनुगमन वेग तथा सचलता क्या है ?
(i) अनुगमन वेग और धारा तथा
(ii) सचलता और धारा के बीच सम्बन्ध स्थापित करें।
उत्तर: अनुगमन वेग (Drift velocity)-किसी चालक को सेल से जोड़ते हैं। इससे इसके सिरों के बीच विभवान्तर स्थापित होता है। चालक के भीतर electron पर विद्युत क्षेत्र काम करने लगता है। इस electron के स्वतंत्र रहने के कारण इसका वेग लगातार बढ़ते रहना चाहिए। परन्तु ऐसा नहीं हो पाता है। इसका कारण यह है कि ये सब electron अपने रास्ते में (+ve) आयनों से टकराकर अपना वेग तथा समान कर लेता है। इस निश्चित माध्य (Mean) वेग को “अनुगमन वेग” (Drift velocity) कहते हैं। इसे V_d से सूचित करते हैं।

सचलता (Mobility)-इकाई विद्युत क्षेत्र में आवेश वाहको (Charge carries) के drift velocity को-“अनुगमन वेग (drift velocity) कहते हैं। इसे “μ” से सूचित करते हैं।

मानलिया कि विद्युत क्षेत्र E तथा drift vel. V_d है।
∴ μ = V_d/E
इसका S.I. unit m²V^-1S^-1 है।

अनुगमन वेग तथा विद्युत धारा के बीच सम्बन्ध (Relation between drift velocity and electric current) –
मानलिया कि एक चालक की लम्बाई l है। इसका अनुप्रस्थ क्षेत्र A है। इसे एक बैट्री से

जोड़ते हैं। इसमें चालक के सिरों के विभवान्तर V हो जाता है। यह चालक में एक विद्युत क्षेत्र E उत्पन्न करता है। E के कारण चालक के अन्दर बायीं ओर अनुगमन वेग V^d उत्पन्न होता है।
मानलिया कि चालक के इकाई आयतन में free election की संख्या अर्थात् घनत्व n है।
परन्तु चालक का आयतन = Al
∴ चालक से free electron की संख्या = nAl
यदि प्रत्येक free electron पर आवेश e हो तो
कुल आवेश =nA te
मानलिया कि आवेश को चालक की लम्बाई (l) तय करने में समय t लगता है।

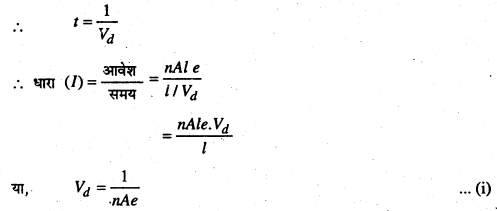
Eq. (i) से drift Velocity तथा धारा के बीच सम्बन्ध प्राप्त होता है। यहाँ पर
n, A तथा e एक स्थिर राशि है।
I α V_d
अर्थात् धारा, drift velocity के समानुपाती होता है।
सचलता तथा धारा के बीच सम्बन्ध-
हम जानते हैं कि

प्रश्न 9. सायक्लोट्रोन क्या है? इसके बनावट, क्रिया, सिद्धान्त तथा सीमाओं का वर्णन करें।
उत्तर: सायक्लोट्रोन (Cyclotron)-
Cyclotron का ऐसा यंत्र है जिससे उच्च गतिज ऊर्जा का proton, dentron, α – कण इत्यादि प्राप्त किया जाता है। यह उच्च ऊर्जा को त्वरित (accelerate) करता है। इसीलिए इसे आवेशित कण त्वरित्र (Charged particle accelerated) भी कहा जाता है। इसे -लारेन्स (Lorentz) तथा Levenston ने बनाया था।

बनावट – इसमें अंग्रेजी के D अक्षर के आकार का दो खोखला बर्तन A और B है। इसके व्यास वाला किनारा समानान्तर रहता है। दोनों के बीच थोड़ी-सी जगह खाली रहती है। इसीलिए दोनों को “डी (Dee)” कहते हैं। इस डी को उच्च आवृत्ति के विद्युत दोलित्र (Electric oscillator) से जोड़ा जाता है। इसकी आवृत्ति लगभग 10⁷ चक्कर/से० तथा विभवान्तर 10⁴ वोल्ट रहता है। A और B को एक बड़े बर्तन में बन्द कर देते हैं। इसके भीतर निम्न दाब पर गैस भरी रहती है। इसमें Proton के लिए H₂ गैस तथा α – कण के लिए H_e गैस ली जाती है।

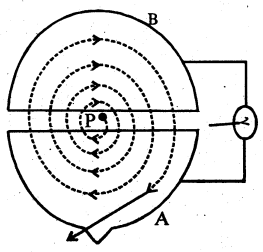
क्रिया – एक (+ve) कण (p) की कल्पना करते हैं। इसका द्रव्यमान m तथा आवेश q हैं। इसे दोनों बर्तन के बीच खाली स्थान में लाया जाता है। यह कण (-ve) विभव वाले बर्तन की ओर त्वरित होता है। मानलिया कि इस समय (-ve) विभव का बर्तन A है। अब A और B को किसी विद्युत चुम्बक द्वारा चुम्बकीय क्षेत्र में इस प्रकार रखा जाता है कि यह इसके सतह के लम्बवत हो। इस समय आवेश अर्द्धवृत्ताकार पथ पर होगा। दोलित्र की आवृत्ति इस तरह adjust की जाती है कि अर्द्धवृत्ताकार पथ पर लगा समय दोलित्र के अर्द्ध आवर्तकाल के बराबर हो। इस स्थिति में (+ve) आवेश दोनों डी के बीच आयेगा तब B का विभव -ve हो जायेगा।

इस समय (+ve) आवेश अधिक वेग के साथ B में प्रवेश करेगा। इससे B में वृत्तीय पथ की त्रिज्या बढ़ जायेगी। यह क्रिया बार-बार दुहराई जाती है। इससे (+ve) आवेश अधिक-से-अधिक वेग प्राप्त कर लेता है। साथ-ही-साथ इसकी ऊर्जा भी बहुत अधिक हो जाती है।

सिद्धान्त (Theory) – मानलिया (+ve) कण पर आवेश q, वेग V तथा चुम्बकीय क्षेत्र B है।

समी० (1) तथा समी० (2) से,

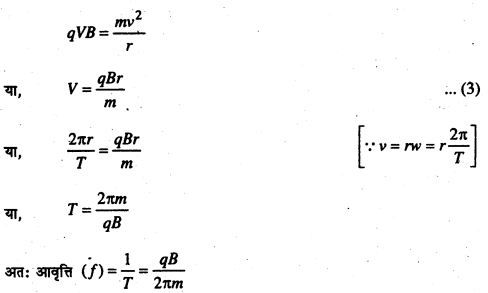
इस आवृत्ति को Cyclotron frequency कहते हैं। इसे “Resonance condition” कहा जाता है।
यदि’r = R (दोनों डी की त्रिज्या) हो तो

उपयोग-(i) नाभिक पर बमबारी करके नाभिकीय प्रतिक्रियायें के अध्ययन में।
(2) ठोस पदार्थों में कणों को रोपित (Implant) करके उनके गुणों के सुधार करने तथा नये पदार्थ को संश्लेषित (Synthesise) करने में।

(3) रोग उपचार के लिए Radio active पदार्थों को उत्पन्न करने में।
सीमा (Limitation)-यहाँ पर हमलोग मानकर चलते हैं कि अधिक वेग पर भी द्रव्यमान स्थिर रहता है। परन्तु Einstein के अनुसार द्रव्यमान वेग के साथ बदलता है। अतः वेग के साथ द्रव्यमान भी बदलेगा। अधिक वेग होने पर वृत्तीय पथ पर चलने में समय बदलेगा। अतः इसका कार्य एक सीमित वेग के अन्दर ही रहेगा।

प्रश्न 10. चल कुण्डली धारामापी का वर्णन करें। सिद्धान्त सहित इसकी क्रिया का वर्णन करें इसकी सुग्राहिता किन बातों पर निर्भर करती है, लिखें।
उत्तर: चल कुण्डली धारामापी (Moving coil Galvenometer)-इस galv. को “डी० आज़ेनोवल” (D.Arsonovol) ने बनाया है। इसलिए इसे “Arsonoval galv.” भी कहते हैं। यह विद्युत धारा मापने का सरल एवं सुग्राही यंत्र है।

बनावट – इसके NS एक शक्तिशाली नाल चुम्बक है। इसके ध्रुव बेलनाकार रहते हैं। इनके बीच नरम लोहा का एक बेलन B रहता है। इस बेलन के दोनों ओर आयताकार कुण्डली लगी रहती है। इस कुण्डली को फॉस्फर ब्रोन्ज (Phosphor Bronze) के तार A से लटका दिया जाता है। यह तार एक संयोजक पेंच D से जुड़ा रहता है। तार के बीच में एक समतल दर्पण

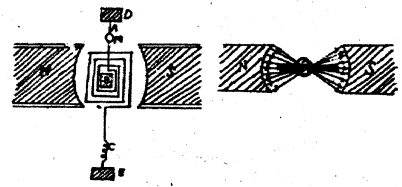
M लग्न रहता है। कुण्डली का दूसरा छोर एक फॉस्फर ब्रोंज की कमानी C से लगी रहती है। यह कमानी भी एक संयोजक पेंच E से जुड़ा रहता है। D और पेंच से कुण्डली में विद्युत धारा प्रवाहित करते हैं। पूरे उपकरण को एक अचुम्बकीय पदार्थ के बक्से में बन्द रखा जाता है। इससे हवा का झोंका या धूलकण नहीं पड़ता है। बक्सा का क्षैतिज करने के लिए आधार में ती

पेंच लगे रहते हैं। मात्र चुम्बक का सतह अवतल (concave) रहने के कारण बेलन B के स्थान में चुम्बकीय क्षेत्र वेज्य (Radial) होता है। इसलिए कुण्डली हमेशा समान चुम्बकीय क्षेत्र में रहती है।

कुण्डली की उदग्र भुजाओं पर चुम्बकीय क्षेत्र हमेशा कुण्डली के सतह के समानान्तर रहता है।

सिद्धान्त – मान लिया कि CDEF एक आयताकार कुण्डली है। इसके CD तथा EF की लम्बाई l तथा CF और DE की लम्बाई b है। यह कुण्डली चुम्बकीय क्षेत्र में लटकती है। कुण्डली में I धारा प्रवाहित किया जाता है। इसमें DE तथा CF पर लगने वाला बल = BI b sin0°

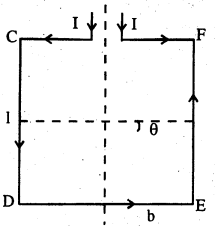
[जहाँ θ = 0 धारा तथा चुम्बकीय क्षेत्र के बीच का कोण]
अतः बल = Blb . 0 = 0
फिर CD तथा EF पर लगने वाला बल = BIl sin 90° [∵ θ = 90°]
= BIl
यहाँ बल CD तथा EF पर विपरीत दिशा में काम करते हैं। अतः यह एक बलयुग्म (Couple) बनाता है।
इस बलयुग्म का आघूर्ण (Moment of the couple)
= बल बल बाहु
= BIl . b
= BIa
जहाँ l . b = a = कुण्डली के एक लपेटन का क्षेत्रफल
यदि कुण्डली में तारों के लपेटनों की संख्या n हो तो
कुल विक्षेपक बलयुग्म का आघूर्ण
= Blan …(i)
इससे कुण्डली विक्षेपित होती है। तार में ऐंठन उत्पन्न होता है। यदि उत्पन्न ऐंठन ले तो
नियंत्रक बलयुग्म का आघूर्ण = kθ …(ii)
जहाँ k ऐंठन स्थिरांक या इकाई ऐंठन के लिए आघूर्ण है।
संतुलन की स्थिति में,
समी० (i) = समी० (ii)
BIna =kθ

(iii) में सभी राशिमान दे देने पर प्रवाहित धारा. I हो जाता है।
k’ के स्थिर होने के साथ I ∝ θ
अतः चल कुण्डली में धारा, विशेष के समानुपाती होता है।
θ का मान निकालना – θ
का मान लैम्प और स्केल व्यवस्था (Lamp and Scale arangement) से निकाला जाता है। इसमें एक Stand पर स्केल के तथा बीच में एक Lamp रहता . है। लैम्प से प्रकाश galv. दर्पण पर आपतित होता है। दर्पण से परावर्तित प्रकाश स्केल पर प्रतीत होता है। जिस धारा को मापना रहता है उसे galv. से प्रवाहित करते हैं। इससे दर्पण घूमता है। परावर्तित प्रकाश स्केल पर Y से X पर चला जाता है।

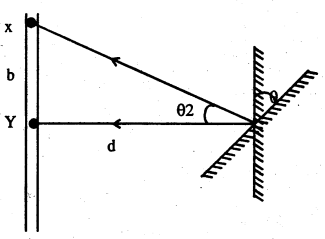
मान लिया कि दर्पण का घुमाव = θ
परावर्तित किरण का घुमाव = ∠YMX = 2θ
फिर मानलिया कि YX = d
तथा दर्पण से स्केल की दूरी = D
ΔYMX से, tan 2θ = d/D
यदि θ कोण छोटा हो तो -tan 2θ = 2θ
2θ = d/D
या,θ = d/2D
प्रयोग से प्राप्त d तथा D का मान दे देने पर θ ज्ञात हो जाता है। फिर इस θ ज्ञात हो जाता है। फिर इस तथा Galv.constant का मान सेमी० (iii) में दे देने पर प्रवाहित धारा का मान ज्ञात हो जाता है।

सुग्रहिता (Sensitivity)

1. B अधिक होना चाहिए
2. n अर्थात् लपेटनों की संख्या अधिक होनी चाहिए
3. a अर्थात् कुण्डली का क्षेत्रफल अधिक होना चाहिए।
4. k कम होना चाहिए। इसके लटकाने वाले तार पतला होना चाहिए।