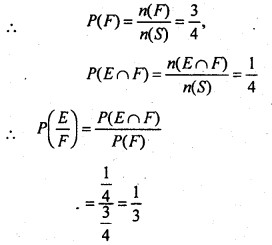Bihar Board 12th Maths Important Questions Short Answer Type Part 2 in Hindi
Bihar Board 12th Maths Important Questions Short Answer Type Part 2 in Hindi
BSEB 12th Maths Important Questions Short Answer Type Part 2 in Hindi
व्युत्पन्न का सिद्धान्त
प्रश्न 1.
त्रिज्या के संदर्भ में एक वृत्त के क्षेत्रफल में परिवर्तन की दर को ज्ञात करें, जबकि विन्या r =5 cm.
उत्तर:
∴ त्रिज्या के वृत्त का क्षेत्रफल A है।
A = πr2
∴ त्रिज्या r के संदर्भ में वृत के क्षेत्रफल Δ में
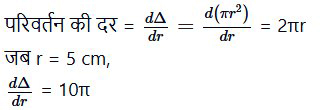
इस प्रकार, वृत्त का क्षेत्रफल में परिवर्तन की दर 10 πcm2/cm से हो रही है।
प्रश्न 2.
दिए गए फलन ‘f’ में दिखाएँ कि
f(x) = x3 – 3x2 + 4x, x ∈ R.
R की ओर बढ़ रहा है ।
उत्तर:
दिया गया है
f(x) = x3 – 3x2 + 4x
f(x) = 3x2 – 6x + 4.
= 3(x2 – 2x + 1) + 1
= 3(x – 1)2 + 1 > OR के सभी interval में।
∴ फलन fR की ओर बढ़ रहा है ।
प्रश्न 3.
दिए गए वक्र y = √4x−3−1 के स्पर्शी पर बिन्दु ज्ञात करें जहाँ उसकी ढाल 2/3 हैं।
उत्तर:
दिए गए वक्र (x, y) के स्पर्शी का ढाल
वक्र के स्पर्श पर बिन्दु (x, y) = (3, 2).
प्रश्न 4.
एक आयत की लम्बाई ‘x’ जो 3 cm/minute की दर से घट रही है तथा · चौड़ाई ‘y’ जो 2 cm/minute की दर से बढ़ रही है जबकि x = 10 cm तथा y = 6 cm. तो निम्न में परिवर्तन की दर को ज्ञात करें। (a) परिमिति
(b) आयत का क्षेत्रफला
उत्तर:
आयत की लम्बाई x से घट रही है तथा चौड़ाई y समय के संदर्भ में बढ़ रही है।
प्रश्नानुसार,
प्रश्न 5.
रेखाओं का समीकरण ज्ञात करें जिसकी ढाल 2 तथा वक्र के स्पर्शी 
है।
उत्तर:
दिए गए वक्र के किसी बिन्दु (x, y) के स्पर्श की ढाल
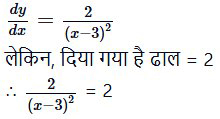
(x – 3)2 = 1
x – 3 = ± 1
∴ x = 4,2
जब x = 2 तो y = 2 तथा x =4 तो y=-2.
∴ वक्र जिसके स्पर्शी की ढाल 2 है। उसके दो स्पर्श रेखा है जो दो बिंदु (2, 2) तथा (4,-2) से होकर जाती है।
∴ स्पर्श रेखा का समीकरण, जो बिंदु (2,2) से होकर जाती है।
y-2 = 2(x-2)
y – 2x + 2 = 0
तथा स्पर्श रेखा का समीकरण जो (4,-2) से गुजर रही है।
y – (-2) = 2(x-4)
y – 2x + 10 = 10
प्रश्न 6.
दिए गए फलन f का उच्चतम तथा न्यूनतम मान ज्ञात करें।
f(x) = 3x2 + 4x3 – 12x2 + 12
उत्तर:
दिया गया है,
f(x) = 3x2 + 4x3 – 12x2 + 12
f(x) = 12x3 + 12x2 -24x
=12x(x-1)(x+2)
f(x) = 0 जहाँ x= 0, x = 1, x = -2
f”(x) = 36x2 + 24x – 24
= 12(3x2 + 2x -1)
f”(0) = -12 <0 ∴ f”(1) = 48 > 0
∴ f”(-2) = 84 > 0
∴ at x =0,f का उच्चतम तथा न्यूनतम मान f (0) = 12 जबकि, x = 1 तथा x=-2 न्यूनतम बिंदु है।
∴ न्यूनतम मान जब x = 1
f(1) = 7
जब . x = -2
f(-2) = -26
समाकलन
प्रश्न 1.
निम्नलिखित का समाकलन ज्ञात करें।
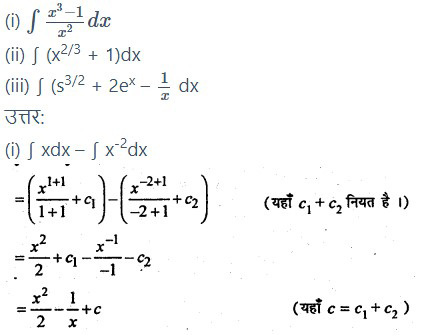
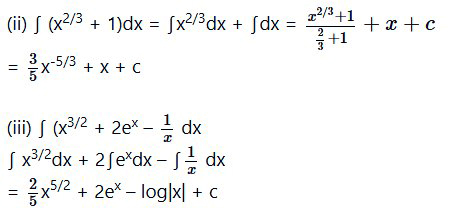
प्रश्न 2.
निम्न का समाकलन ज्ञात करें
(i) ∫sin x + cos x)dx
(ii) ∫ cosec x(cosec x + cot x)dx
(iii) 
उत्तर:
(i) ∫sin x + cos x)dx
= ∫sin x.dx + ∫cosx.dx = -cosx + sinx+c
(ii) ∫cosec x(cosecx+cotx)dx.
= ∫cosec2 x + ∫cosecx.cotx dx
= -cotx – cosecx + c
(iii)
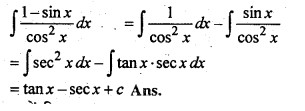
प्रश्न 3.
x के पक्ष में निम्न फलन का समाकलन ज्ञात करें
(i) sin mx
(ii) 2x sin(x2 + 1)
(iii) tan4 √x sec2 √x
उत्तर:
(i) हम जानते हैं कि mx का derivative m है। इस प्रकार साबित mx = 1 साबित करें mdx = dt
∵ ∫sin mx dx = ∫1/m ∫sin t dt
= -1/m cos t + c = -1/m cos mx + c
(ii) 2x का derivative x2 + 1 है
इस प्रकार x2 + 1 = t साबित करें 2x.1 = dx = dt
∵ 2xsin (x2 + 1 )dx
= ∫sin t.dt
= -cos t + c
= -cos (x2 + 1 ) + c
प्रश्न 4.
ज्ञात करें ∫ x cos x dx
उत्तर:
∫ x cos x dx
= x∫cosx. dx – ∫ [ d/dx (x)∫cos x.dx ]dx
= xsin x – ∫ sin x dx
= xsinx + cosx + c
प्रश्न 5.
प्रश्न 6.
ज्ञात करें : ∫ ex sin x dx
उत्तर:
माना I = ∫ ex sin x dx
= ex∫sin x dx – ∫(dex/dx∫ sin x)dx
I = ex(-cos x) – ∫ex(-cos x) dx
I = -excos x + ∫excos dx
I = -ex cos x + ex sin x – ∫ex sin x dx
I = -ex cos x + exsin x – I + c
2I = ex(sin x – cos x) + c
I = ( sin x – cos x) + c
प्रश्न 7.
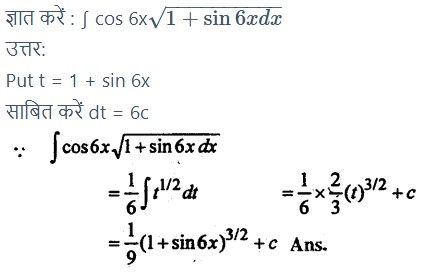
प्रश्न 8.
Differential Equation
प्रश्न 1.
वकल समीकरण
प्रश्न 1.
दिये गये अवकल समीकरण का क्रम और घात ज्ञात करें :
प्रश्न 2.
वक्र y2 = a2(b2 – x2) का अवकल समीकरण ज्ञात करें।
उत्तर:
दिया गया समीकरण y2 = a2(b2 – x2) …….(i)
Diff. w.r. to x
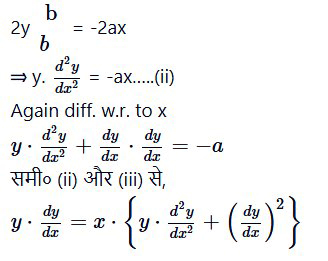
प्रश्न 3.
Family of curve x2 + y2 = 2ax से अवकल समीकरण बनायें।
उत्तर:
Given equation x2 + y2 = 2ax
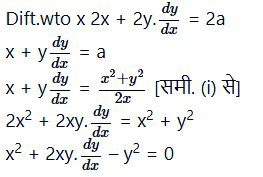
प्रश्न 4.
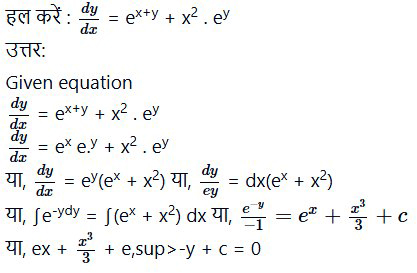
प्रश्न 5.
हल करें : (x2 – yx2 ) dy = (y2 + x2y2)ds = 0
उत्तर:
(x2 – yx2 ) dy = (y2 + x2y2)ds = 0
या, (x2 – yx2)dy = (y2 + x2y2)dx
या, x2(1 – y) dy = -y2 (1 + x2)dx
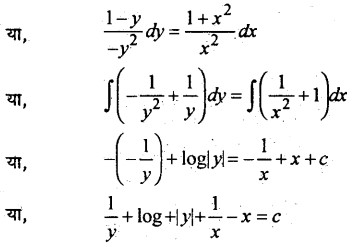
Vector Algebra
प्रश्न 1.
प्रश्न 2.
प्रश्न 3.
प्रश्न 4.
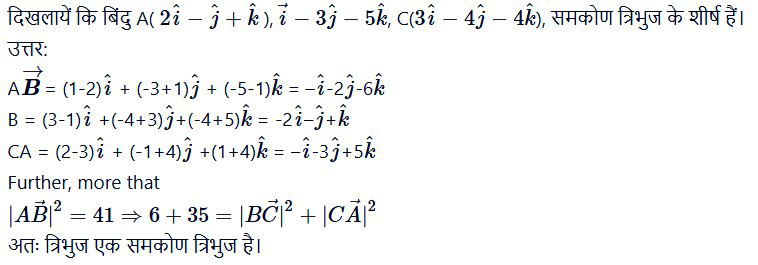
प्रश्न 5.
प्रश्न 6.
प्रश्न 7.
प्रश्न 8.
त्रिविमिय ज्यामिति
प्रश्न 1.
दिखाएँ कि बिन्दु A (2,3,-4), B(1,-2,3) तथा C (38, -11) रैखिक है।
उत्तर:
रेखा का दिक् अनुपात जो A तथा B को जोड़ता है । 1-2,-2-3,3+4 अर्थात् -1,-5, 7. – रेखा का दिक् अनुपात जो B तथा C को जोड़ता है =3-1,8+2,-11-3 अर्थात् 2, 10, -14 है।
यह स्पष्ट है कि AB तथा BC का दिक् अनुपात समानुपाती है। अत: AB, BC का समानान्तर है लेकिन बिन्दु B, AB तथा AB दोनों का उभयनिष्ठ है। इसलिए A, B, C, रैखिक बिन्दु है।
प्रश्न 2.
यदि एक रेखा के 2,-1,-2 हो तो इसका दिक् कोज्या ज्ञात करें ।
उत्तर:
दिक् कोज्या =
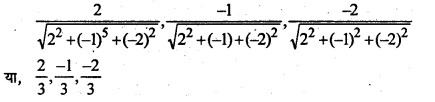
प्रश्न 3.
रेखा के दिक् कोज्या ज्ञात करें जो दो बिन्दु (-2, 4, -5) तथा (1, 2, 3) से होकर गुजरता है।
उत्तर:
हमलोग जानते हैं कि रेखा के दिक् कोज्या जो दो दिये गये बिन्दु P(x1,y1, z1) तथा (x2,y2, z2) से गुजरते हैं।
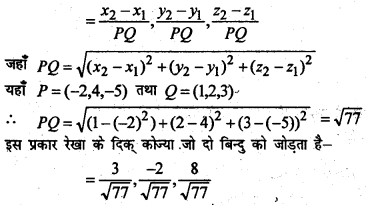
प्रश्न 4.
सतह या तल का समीकरण ज्ञात करें जिसका कटान बिन्दु x, y तथा : अक्षों के साथ क्रमशः 2,3 तथा 4 है।
उत्तर:
माना कि सतह का समीकरण
प्रश्न 5.
प्रश्न 6.
बिन्दु (2, 5, –3) से दिये गये सतह की दूरी ज्ञात करें।
प्रायिकता
प्रश्न 1.
एक पासे के उछाल में 3 के गुणज आने की घटना E तथा सम संख्या आने के घटना F हो तो जाँचें कि E तथा F परस्पर स्वतंत्र घटना है।
उत्तर:
एक पासे के उछाल में n (S) = {1, 2, 3, 4, 5,6}
E = {3,6}
F = {2,4,6},
E∩F = {6}
प्रश्न 2.
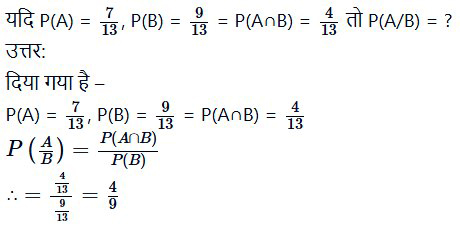
प्रश्न 3.
एक परिवार के दो बच्चों में कम से कम एक लड़का हो तो इसकी क्या प्रायिकता है कि दोनों बच्चे लड़के ही हों ?
उत्तर:
माना कि लड़का तथा लड़की के लिए संकेत क्रमशः b तथा 8 है ।
∴ Sample slape (S) = { (b, b), (8,b), (b.8), (8.8)}
माना कि E = दोनों बच्चे के लड़के होने की घटना
F = कम से कम एक बच्चे के लड़के होने की घटना
∴ E = { (b, b)}, F = {(b, b), (g, b), (b, 8)}
∴ E ∩ F = {(b,b)}
