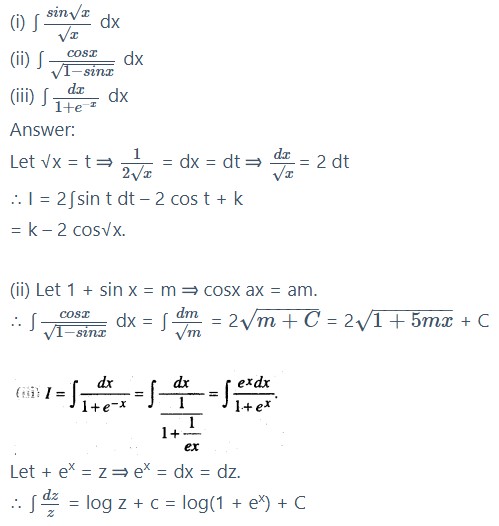Bihar Board 12th Maths Important Questions Short Answer Type Part 1 in English

Bihar Board 12th Maths Important Questions Short Answer Type Part 1 in English

BSEB 12th Maths Important Questions Short Answer Type Part 1 in English

Relation & Functions

Question 1.
Prove that the function f :R→R given by f(x) = 2x is one-one & on to.
Solution:
For one-one – Take f(x₁) = f(x₂) .
⇒ 2x₁ = 2x₂
⇒ x₁ = x₂
∴ f is one-one.
For on to co-domain = R
Rage = y = 2x = 2 x R = R
∴ Co-domain = Rage
∴ f is on to
Hence f is one-one onto.

Question 2.
Show that the function f: N → N given by f(1) = f(2) = 1 & f(x) = x-1 for every x > 2 is on to but not one-one,
Solution:
∴ f(1) = f(2) = 1
∴ f is not one-one
∴ f(x) = x – 1
∵ Co -domain = N
∀ x > 2, Rage = N
∴ Co-domain = Rage
∴ f(x) is on to.

Question 3.
Let L be the set of all lines in a plane and# he the relation inL defined as R = { (L₁ L₂) : L₁ is perpendicular to L₂). Show that R is symmetric but neither reflexive nor transitive.
Answer:
a line L₁ can not be ⊥r to itself.
R is not reflexive.
For symmetric — If L₁ RL₂
⇒ L₂RL₁

⇒ L₁ is ⊥r to L₂
⇒ L₂ is ⊥r to L₁
⇒ (L₂,L₁) ∈ R.
∴ R is symmetric
for transitive — If L₁ RL₂, L₂RL₃ = L₁RL₃
Given is ⇒ L₁ is ⊥r L₂
& . L2 is lr L3
⇒ L₁||L₃
⇒ L₁ is ⊥r L₂
⇒ L₂ is ⊥r L₃
⇒ L₁||L₃
∴ R is not transitive.

Question 4.
Show that the function f:R→R: f(x) =x³ is one-one and onto.
Solution:
Given, f(x₁) = f(x₂) ⇒ x₁³ = x₂³

⇒ x₁ = x₂
⇒ f is one-one.
Let y ∈ R and 3; = x³; Then x = y^1/3 e R.
Thus, for each y in the codonain R there exists y^1/3 in R such that
f(y^1/3) = (y^1/3)³ = y
⇒ f is onto.
Hence, f is one-one to.

Matrix

Question 1.

Question 2.

Question 3.

Question 4.

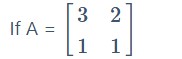
Find the number a and b such that A² + aA + bI = 0 where I is an identity matrix of order 2×2 and 0 is a 2 x 2 Zero matrix.
Solution:

Equation the respective elements of two matrices we get.
8 + 2a = 0 ⇒ a =—4
and 11 + 3a + b = 0 ⇒ 11 – 12 + b = 0 ⇒ b= 1
Hence .
a = -4, b = 1.

Determinants

Question 1.

Question 2.
Find the area of the triangle with vertices (-2,-3), (3,2) and (-1,-8).
Answer:

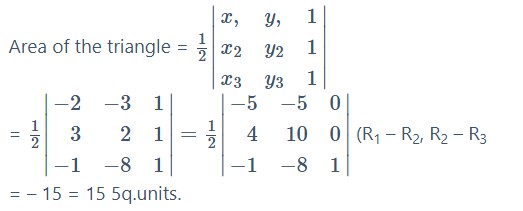
Question 3.
Find Values of k if area of triangle is 4 Sq. units and vertices are : (k, 0), (4,0)’, (0,2).
Solution:

Inverse circular Function

Question 1.

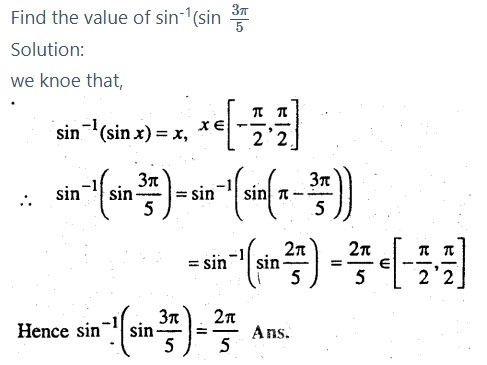
Question 2.

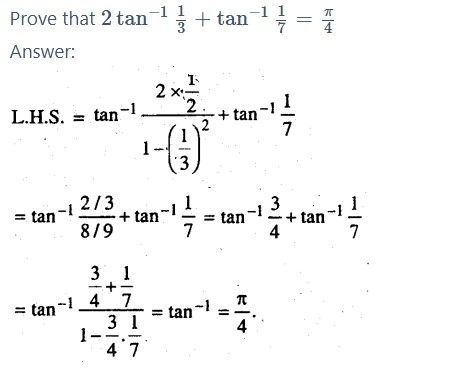
Question 3.

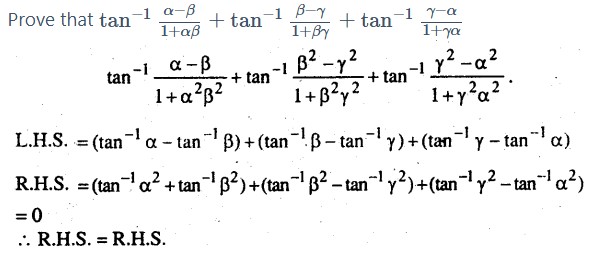
Question 4.

Question 5.
Solve 2tan^-1(cosx) = tan^-1(2 cosec x)
Answer:

Question 6.

Question 7.
sin^-1(1 – x) – 2sin^-1 x – π/2 then x is equal to
(A) 0, 1/2
(B) 1, 1/2
(C) 0
(D) 1/2
Solution:
sin^-1(1 – x) – 2sin^-1 x – π/2
Putting π/2 = sin^-1(1 – x) + cos^-1 (1-x)
-2sin^-1 = cos^-1(x-1)
Let sin^-1 = α
-2sin^-1 = -2α = cos^-1(x-1)
or cos 2α = 1 – x
1 – 2cos²α = (1 – x)
Putting sin α = x
1 – 2x² = 1 – x
or 2x²-x = 0
x(2x – 1) = 0 x = 0, 1/2
But x = 1/2 does not satisfy the equation ∴ x = 0
∴ Part (C) is the correct answer.

Continuity and Differentiabiilty

Question 1.
f(x) = x sin 1/x , x ≠ 0 and f(0) = 0.
Solution:

So, function is continous at x = 0

Question 2.
Prove that every differentiable function is continuous also.
Solution:
Let the function f(x) is differentiable at x = a.

Differentiation

Question 1.
Differentiate the following w.r.t to x.

(viii) Let y = (logx)x
⇒ log y = log x log (log x)
differentiablity w. r. for , we get

(ix) Let y = x^x = e^xlogex
With restpect to x

(x) Let y = (log)^x + x^logx
y = e^{logex + elogex. log_ex}
Diff With respect to x

(xi) Let y = cos (a cos x + bsin x)
⇒ dy/dx = -sin (a cos x + b sin x_) d/dx (acos x +b sin x)
= -sin(a cos x + b sin x ). (-a sin x + b cos x)

(xii) Let y = e^cos-1x
cos^-1x.lo_e^x
or y = e
Diff With respect to x

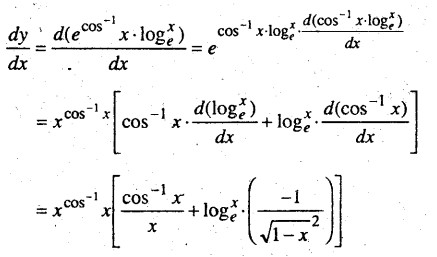
(xiii) Let y = e^sinx + (tanx)^x + (tan x)^x = e^sinx + e^xlog_e tan x
Diff w.r.to x

Question 2.

Question 3.

Question 4.

Question 5.

Question 6.
Integrate the following