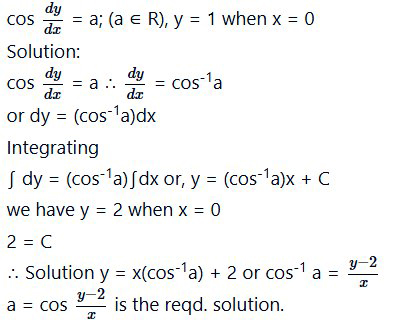Bihar Board 12th Maths Important Questions Long Answer Type Part 5 in English

21 April 2025

BSEB 12th Maths Important Questions Long Answer Type Part 5 in English

Application Of Integrals

Question 1.
Find the area of the region in the first quadrant enclosed by the x-axis, the liney = x and the circle x² + y² = 32
Solution:
The given equations are
y = x …(i)
and x² + y² = 32 …(ii)
Solving (i) and (ii), we find that the line and’the-circle meet at B (4,4) in, the first quadrant., Draw perpendicular BM to the x- axis.
Therefore, the required area = area of the region OBMO + area of the region BMAB. ,
Now, the area of the region OBMO

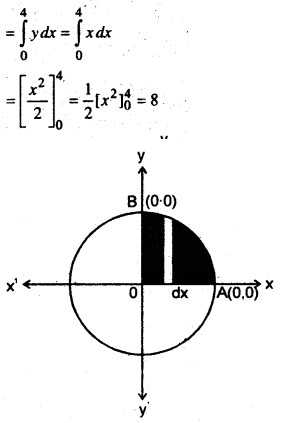
Again, the area of the region BMAB

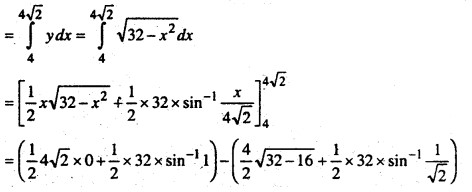
Adding (iii) and (iv), we get
the required area = 8 + 4π – 8
= 4π

Question 2.
Find the area bounded by the ellipse x²/a²+y²/b₂ and the cordinates x = 0 and x = ae, where b² = a² (1 – e²) and e < 1.
Solution:
The required area of the region BOB’RFSB us enclosed by the ellipse and the line x = 0 and x = ae

Now, the area of the region BOBRFSB
Bihar Board 12th Maths Important Questions Long Answer Type Part 5 5

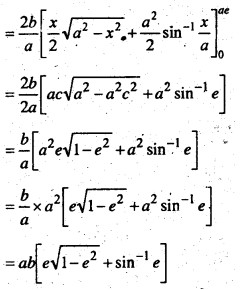
Question 3.
Find the area of the parabola y² = 4ax bounded by its locus rectum.
Solution:
The vertex of the parabola y² = 4ax is at origin (0,0).
The equation of the locus rectum ∠SL’ is x = a. Also, parabola is symmetrical about the x-axis.
The required area of the region OLL’ = 2 (area of the region OLSO).

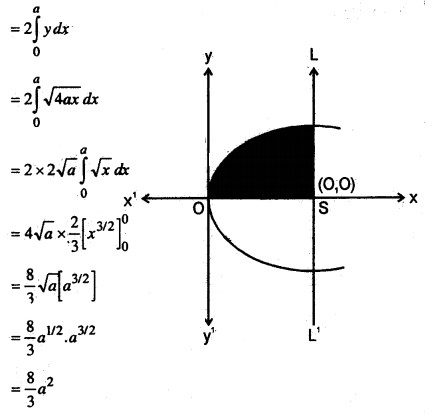
Question 4.
Form the differential equation representing the family of curves y = a sin (x + b), where a, b are arbitrary constants.
Solution:
We have
y = a sin {x + b) ………….(i)
Differentiating both sides of the eqn. (i)
with respect to x, we get

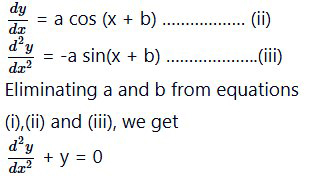
Which is free form the arbitrary constants a and b hence this the required differential equation.

Question 5.
Find the general solution of the differential equation.

Question 6.
Find the particular solution of the differential equation

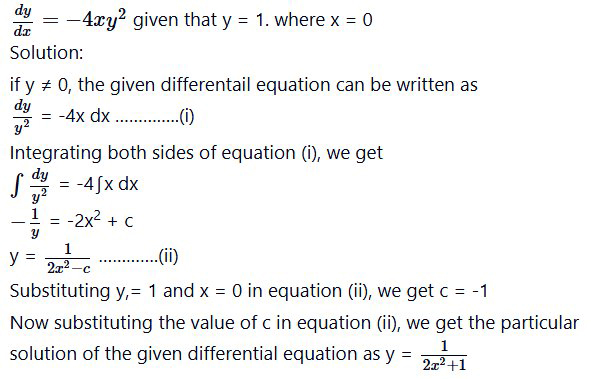
Question 7.
Show that the differential equation x – y dy/dx = x + 2y is homogeneous and solve It.
Solution:
The given differential equation can be expressed as dy x + 2y

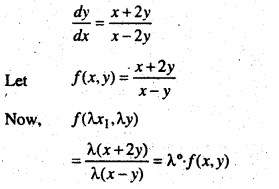
Therefore, f(x, y) is a homogenous function of degree zero. So, the given differential equation is a homogenous differential equation.

Question 8.
Find the general solution of the differential equation

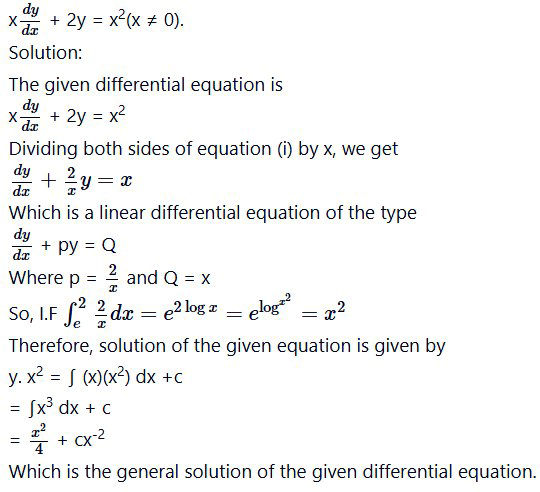
Question 9.
Solve the differential equation
(tan^-1 y – x)dy = (1 + y²)dx
Solution:
The given differential eqn. can be written as

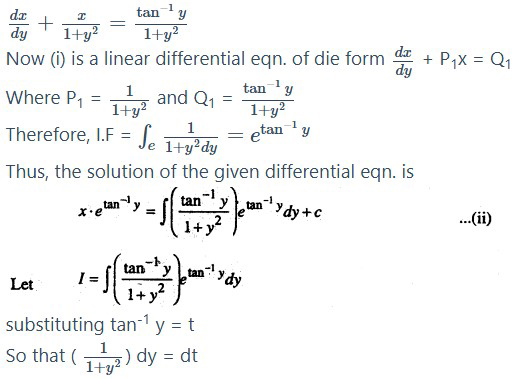
I = ∫te^tdt = te^t – ∫1.e^tdt = te^t – e^t
= e^t (t – 1)
I = e^tan-1(tan^-1 y – 1)
Substituting the value of l in eqn. (ii), we get
x etan^-1y = e tan^-1 y(tan^-1 y – 1) + c
or, x = (tan^-1y – 1) + c e^-tan-1y
Which is the general solution of the given differential equation.

Question 10.
Find the area enclosed by the circle x² + y² = a².
Solution:
The whole area enclosed by the given circle = 4 (area of the region AOBA bounded by the curve, x-axis and the ordinates x-0 and(x = a)

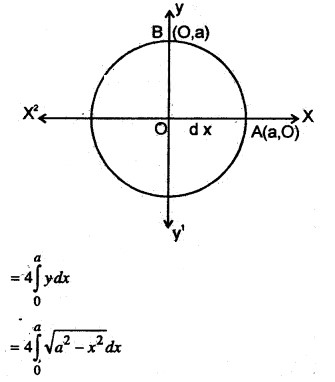
As the region AOBA lies in the first quadrant y is taken as positive.
Integrating, we get the whole area enclosed by die given circle.
Bihar Board 12th Maths Important Questions Long Answer Type Part 5 11

Differential Equation

Question 1.
Solve x cos(y/x)(ydx + xdy) = ysin(y/x)(xdy – ydx).
Solution :
Put y = vx ⇒ dy = vdx + xdv
So the given equation becomes
x cos v(xvdx + xvdx + x² dv) = vx sin v(yxdx + x² dv – vxdx)
⇒ x² cosv(2vdx+xdv) = vx² sinvdv
⇒ 2vdx + xdv = vx tan vdv.
Dividing both sides by vac
⇒ 2dx/x+dv/v = tan v dv. Intergrating, we get
2logx + logv = logseev + logc
x²v = cseev xy = c sec ((x/y))

Question 2.
Solve (1 + y²)dx = (tan^-1 y – x)dy.

Question 3.

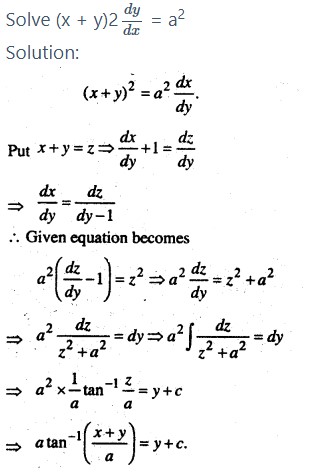
Question 4.

Question 5.

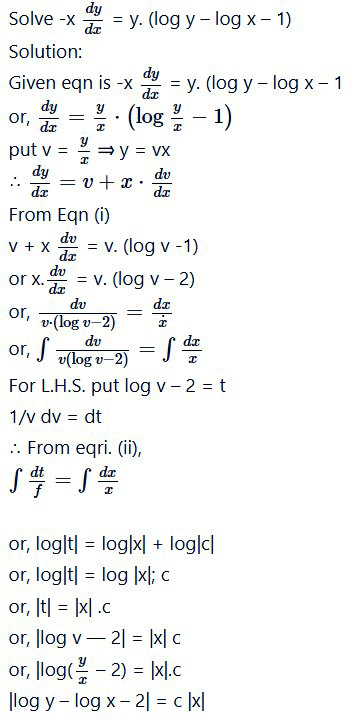
Question 6.

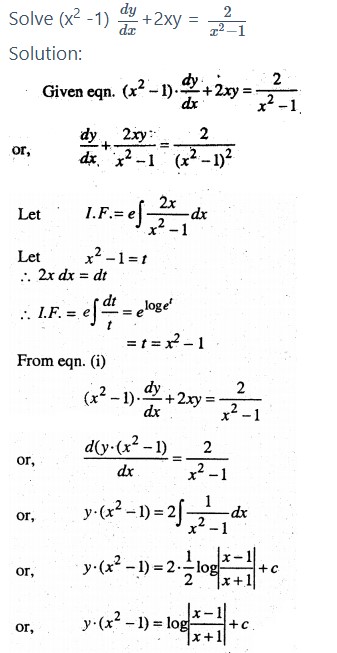
Question 7.

or, 2 = -2 + c
c = 4
From eqn. (ii)
y = -2sin²x + 4sin³ x

Question 8.

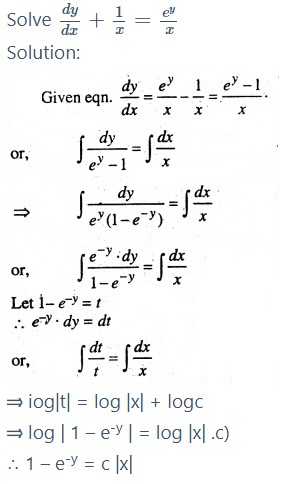
Question 9.

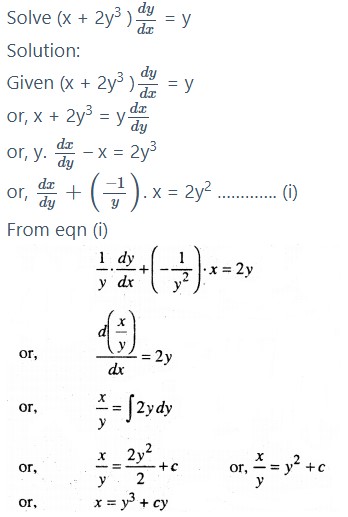
Question 10.

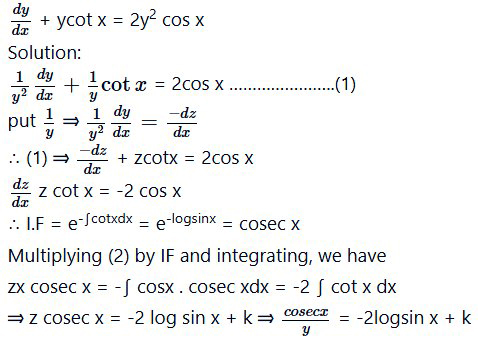
Question 11.
dy/dx + y sec x = tan x
Solution:
I. F = e^∫secx dx = e^{∫log(sec+tanx)} = sec x + tan x
Multiplying the given eqn. with I.F.and integrating we get.
∴ y x (sec x + tan x) =∫ tanx(secx + tanx)dx
= ∫ tanx secx dx + ∫ (sec²x – 1)dx
⇒ y(secx + tan x) = sec x + tan x – x + k.

Question 12.
Evaluate ∫sec³ xdx
Solution:
I = ∫sec³ xdx = ∫sec² x.sec xdx
⇒ I = secx∫sec²xdx – ∫ [d/dx (secx)∫sec²xdx]dx
= secx tanx – ∫secx – tanx tanxdx
= sec x tanx- ∫sec x(sec² x – 1)dx
= sec x tan x – ∫sec³ xdx + ∫secdx
= secx tanx – I + log(secx + tanx) + k
⇒ 2I = sec x . tan x + log (secx + tan x) + k
⇒ I = 1/2 secx tanx + 1/2 log(secx + tanx) + c .