Bihar Board 12th Maths Important Questions Long Answer Type Part 4 in English
Bihar Board 12th Maths Important Questions Long Answer Type Part 4 in English
BSEB 12th Maths Important Questions Long Answer Type Part 4 in English
Application of derivatives
Question 1.
The volume of cube is increasing at a rate of 9 cubic centime Ires per second. How fast is the surface area increasing when the length of an edge is 10 centimetres ?
Solution:
Let x be the length of a side
v be the volume and
S be the surface areas of the cube
then v = x3
and S = 6x2, where x is a function of time t.

Question 2.
Find the intervals in which the function f given by f(x) = sinx + cosx, 0 ≤ x ≤ 2π is strictly increasing or strictly decreasing.
Solution:
We have
f(x) = sin x + cos x
f(x) = cosx-sinx
Now, f'(x) = 0
gives sin x= cos x which gives that


Question 3.

Question 4.
Find the equations of the tangent and normal to be the curve x2/3 + y2/3 = 2 at (1, 1)
Solution:
Differentiating x2/3 + y2/3 = 2 with respect to x, we get


Question 5.
Use differential to approximate √36−6
Solution:
Take y = √x
Let x = 36 and let Δx = 0.6 then

Now dy is approximate equal to Δy and is given by

(as y = √x
Thus, the approximate value of √36.6 is 6 + 0 05 = 6.05.
Question 6.
Use differential to approximate (25)1/3
Solution:
Let y = x1/3
Let x = 27 and let Δx = -2 then
Δy = (x + Δr)1/3 – x1/3 = (25)1/3 – (27)1/3
= (25)1/3 – 3
or, (25)1/3 = 3 + Δy
Now dy is approximately equal to Δy and is given by

Thus, the approximate value of (25)1/3 is given by 3 + (-0.074) = 2.926
Question 7.
Find the approximate value of 3412, where f(x) = 3x2 + 5x + 3.
Solution:
Let x = 3 and Δx = 0.02 Then
f(3.02) = f(u + Δx)
= 3(x + Δx)2 + 5( x + Δx) + 3
Note that Δy = f(x+Δx) – f(x) ‘
Therefore, f(x + Δr)f(x)+Δy
= f(x) + f'(x)Δx (as dx = Δx)
f(3.02) = (3x2 + 5x + 3) + (6x + 5)Δx
= (3(3)2 + 5(3) + 3} + {6(3) + 5}(0.02)Δx
_ (as x = 3, Δx = 0.02)
= (27 + 15 + 3) + (18 + 5)(0.02)
= 45 + 0.46 = 45.46
Hence, approximate value of f( 3.62) is 45.46
Question 8.
Find the approximate change in the volume v of a cube of side x meters caused by increasing the side by 2%.
Solution:
Note that
y = x3
or dv = (dv/dx)Δx = (3x2)Δx
= (3x2) (002x) = 006 x3 m3 at 2% of x is 002x.
Thus, the approximate change in yolume is 0 06 x3 m3
Question 9.
A car starts from a point p at time t = 0 seconds and stops a point Q. The distance x in metres covered by it in t seconds is given b x = t2(2 – t/3)
Find the time taken by it to reach Q and also find distance between i and Q.
Solution:
Let v be the velocity of the car at t seconds.
Now x = t2(2 – t/3)
∴ v = dx/dt = 4r – t2 = t(4 – t)
Thus v = 0 gives t = 0 and/or t = 4 ’
Now v = 0 at P as well as at Q and at P, t- 0.
so, at Q. t = 4.
Thus the car will reach the point Q after 4 seconds. Also the distance travelled in 4 seconds is given by
[x]t = 4 = 42(2 – 4/3
= 16( 2/3 ) = 32/3m
Question 10.
A mail of height 2 metres walks at a uniform speed of 5 km/h s* way from a lamp post which is 6 metres high. Find the rate at which the length of his shadow increases.
Solution:
Let AB be the lamp-post, the lamp being at the position Band let MN be the man at a particular time t and Let AM= l metres. Then MS is the shadow of the man. Let MS = S metres.

Question 11.

Integrals
Question 1.
find the following integrals :
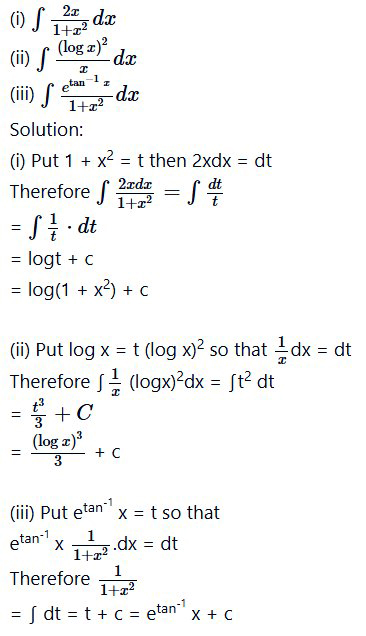
Question 2.
Find the following integrals :
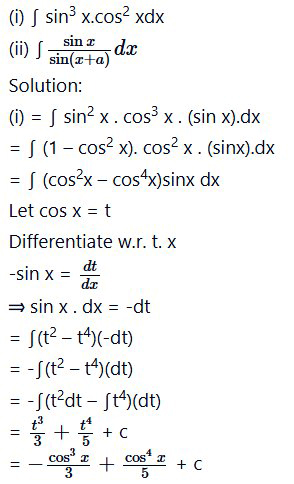
(ii) Put x + a = t
Then dx = dt

= cosa∫dt – sina∫cott dt
= (cos a) t -sin a [ log | sin t| + c1]
= (cos a) ( x +a) – sin a [ log | sin {x + a)| + Cj]
= x cos a + a cos a – sin a log | sin (x+a) |+ c

Question 3.
Find the following integrals:
(i) ∫cos2x.dx
(ii) ∫sin 2x. cos3x. dx
(iii) ∫sin3xdx
Solution:
(i) We know that
cos2x = 2cos2 x – 1
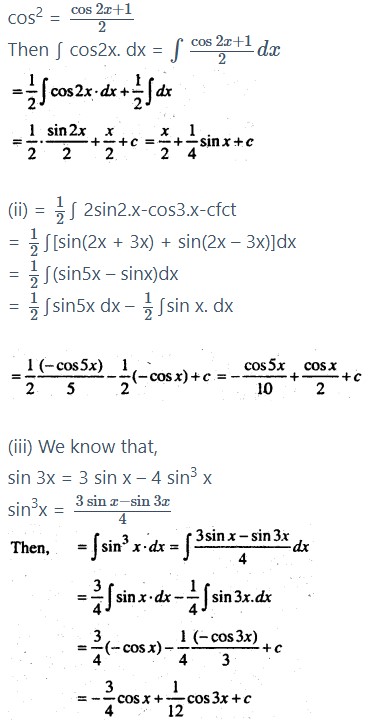
Question 4.
Find the following integrals : dx t dx
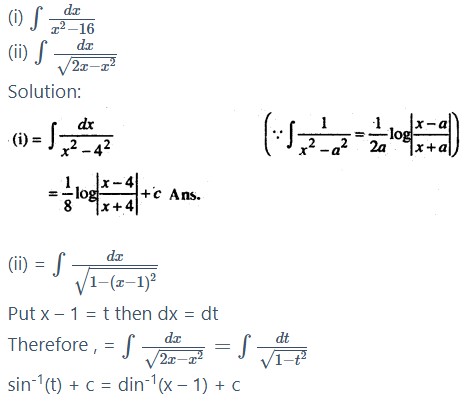
Question 5.

Question 6.

Question 7.

Question 8.

Question 9.
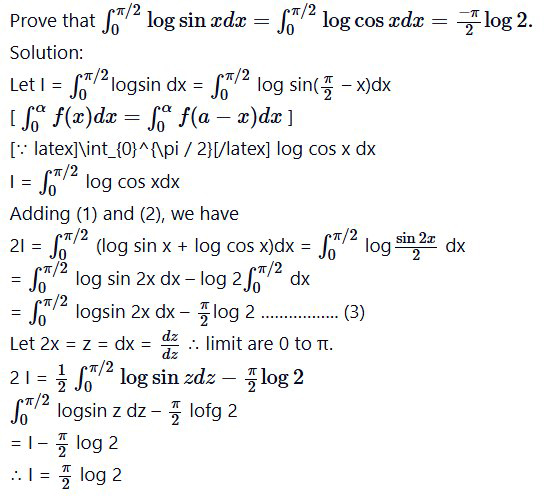
Question 10.
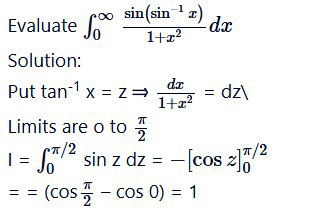
Question 11.
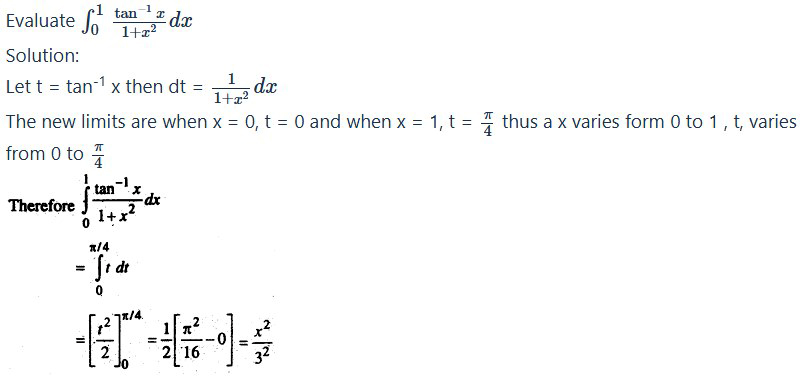
Question 12.

Question 13.
Evaluate sin4θ cos4θ dθ
Solution:
