Bihar Board 12th Maths Important Questions Long Answer Type Part 2 in English

Bihar Board 12th Maths Important Questions Long Answer Type Part 2 in English

BSEB 12th Maths Important Questions Long Answer Type Part 2 in English

Determinants

Question 1.
Using the property of determinants and without expending, prove that

Question 2.

= (a-b) (b-c)-(b² +bc+c² -a²-ab-b²)
= (a-b)-(b-c)-{(c2-a2) + b-(c-a)}
= (a-b)(b-c)-{(c-a)(c + a) + b-(c-a)}
= (a-b)(b-c)-(c-a)(c + a + b)
= (a-b)(b-c)-(c-a)-(a + b+c) R.H.S.

Question 3.

Question 4.
Without expanding prove that

Question 5.

Question 6.
Without expanding shw that,

Question 7.

= x(-x² – 1) – sinθ.(-xsinθ – cos θ) + cos θ(-sin θ + x cos θ)
= -x³ – x + xsin²θ + sin θ.cos θ – sin θ.cos θ + xcos²θ
= -x³.x + x.(sin²θ + cos²θ)
= -x³ – x + x.1
= -x³ – x + x
= -x³ = indepentdent

Question 8.
Evaluate :

= (1 – x)²(1 + x + x²)(1) + x(1 + x)
= (1 – x)² (1 + x + x²)[1 + x + x²]
= (1 – x)²(1 + x + x² )²
= [(1 – x)(1 + x + x² )]² = (1 – x³)²

Question 9.
Evaluate :

Expanding we get
Δ = (1 + a +b2)² (1 – a² – b²) + 2a² + 2b²
= (1 + a² + b² )² (1 + a² + b²) = (1 + a² + b²)³

Question 10.
Evaluate :

= abc  + (b²c² – b²c²) + (a²c² – a²c²) + (a²b² – a²b²) + a² +b² + c²
= a² + b² + c²

Inverse Circular Function

Question 1.
Show the following :

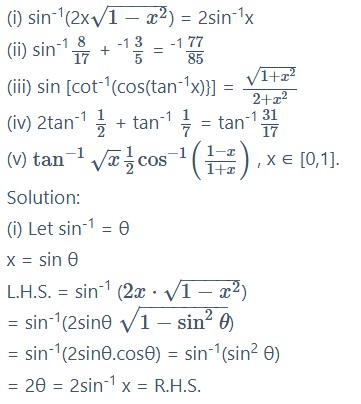
Question 2.
Find the values of each of the following :

Question 3.

Question 4.